Beszámoló a versenyről
A Nemzetközi Magyar Matematikaverseny 1992-ben Oláh György felvidéki és Bencze Mihály erdélyi matematikatanárok kezdeményezésére jött létre azzal a céllal, hogy a Kárpát-medence magyar középiskolásai anyanyelvükön versenyezhessenek matematikából.
A verseny helyszínét kétévente felváltva Magyarország, illetve valamely határon túli város biztosítja. Kaposváron 1997 után már másodszor szólalt meg 2018. március 14—18. között az „ötágú síp”, a Kaposvári Táncsics Mihály Gimnázium szervezésében. A Kárpát-medence öt régiójából — Délvidék, Erdély, Felvidék, Kárpátalja, Magyarország — összesen közel 250 diák és 80 tanár vett részt a versenyen.
A vendégek március 14-én érkeztek a Klebelsberg Középiskolai Kollégiumba. Március 15-én a rendezvény összes résztvevője a Táncsics Gimnázium közösségével együtt ünnepelt a városi megemlékezésén, ahol az öt régióvezető koszorút helyezett el a Kossuth téren. Délután a Táncsics Gimnáziumban az ünnepélyes megnyitóval folytatódott a program.


A versenyző diákok péntek délelőtt megírták a négyórás versenyt, a tanárokat pedig Szita Károly, Kaposvár Megyei Jogú Város polgármestere fogadta a Városháza dísztermében. Délután a zsűri vezetésével elkezdődött a versenydolgozatok javítása, mialatt a tanulók a Virágfürdőben és kaposvári sétán lazítottak. Este vacsora után mindenki az Experidance fergeteges előadásán vett részt a sportcsarnokban. A szombati nap egésznapos kirándulással és búcsúvacsorával telt.
Március 18-án a rendezvény ünnepélyes záróműsorral ért véget, amelynek keretében sor került a verseny szakmai értékelésére, a régióvezetők hozzászólásaira, valamint az ünnepélyes eredményhirdetésre.

A szervezők és a zsűri, amelynek elnöke Szalay István, a Szegedi Tudományegyetem címzetes egyetemi tanára, az idei évben 11 első díjat, 10 második díjat, 20 harmadik díjat és 60 dicséretet adtak ki a versenyzőknek. Emellett hagyományosan díjazásra kerültek a különböző régiók legeredményesebb versenyzői, minden évfolyam abszolút győztesei. Az idén a zsűri különösen szép feladatmegoldásért is adott ki díjakat. Az idei év volt a harmadik, amikor a verseny egyik alapítójáról, Dr. Urbán Jánosról elnevezett díj is gazdára talált egy határainkon belüli és egy határainkon kívül élő tanulónál.
A négy évfolyam feladatsora és megoldásai a Kaposvári Táncsics Mihály Gimnázium honlapjáról tölthetők le.
A XXVII. NMMV tapasztalatai a zsűrielnök szemével
Előzményként szeretném elmondani, hogy a zsűri (Csorba Ferenc, Katz Sándor, Laczkó László, Pintér Ferenc, Szalay István) köszönetet mond a kitűzendő feladatokra javaslatot küldő kollégáknak: Ágó Balog Krisztina (Újvidéki Egyetem), Bíró Bálint (Eger), Bíró Béla (Sepsiszentgyörgy), Bencze Mihály (Bukarest), Borbély József (Óbudai Egyetem), Csikós Pajor Gabriella (Szabadka), Erdős Gábor (Nagykanizsa), Fedorszki Gábor (Beregszász), Kekenac Szilvia (Kassa), Kekenac Tamás (Kassa), Kiss Sándor (Nyíregyháza), Kovács Bálint (Székelyudvarhely), Kovács Béla (Szatmárnémeti), Kovács Lajos (Székelyudvarhely), Molnár István (Gyula), Nemecskó István (Budapest), Németh László (Fonyód), Péics Hajnalka (Szabadka), Róka Sándor (Nyíregyháza), Szabó Magda (Szabadka), Szoldatics József (Budapest), Tóth Sándor (Kisvárda), Tóth Viktor (Cambridge), Vistanova Laura (Kassa), Vistan Miko (Kassa). Természetesen a zsűri tagjai is küldtek be javaslatokat.
Végül a zsűri 182 feladat közül választotta ki az évfolyamként 6-6 összesen 24 feladatot, amelyek a versenyen kitűzésre kerültek. A kiválasztott feladatok közül a magyarországi régióból származott 16, Erdélyből 2, Felvidékről 2, Délvidékről 2 és Kárpátaljáról is 2. Minden évfolyam feladatai közé került határon túli szerzőtől származó feladat. Szempont volt az is, hogy bár minden feladat minimális pontszáma 1, maximális pontszáma 10 volt, a feladatok első harmada a „könnyebb” második harmada a „közepesen nehéz” és utolsó „harmada” a „nehezebb” kategóriából kerüljön ki. Köszönet illeti a dolgozatokat javító kollégákat is, akiknek munkáját a zsűri a szerzők által beküldött megoldásokon túlmenően, a javítási útmutatóban újabb, megoldásokkal segítette. (A kitűzött feladatok és megoldásaik a itt érhetők el.) A továbbiakban ezekből ragadunk ki — elsősorban az oktatás szempontjából — megszívlelhető tanulságokat. (A verseny részletes eredményeit nem taglaljuk, azokból csak epizódokat ragadunk ki.)
9. évfolyam
(Javító tanárok a feladatok sorrendjében: Árokszállási Eszter, Dr. Minda Mihály, Cziprok Tamás; Kováts Márta, Gazdag Jolán; Breining Beáta, Portik Antal; Liszkay Béla, Héder Éva, Szittyai István; Kovács Béla, Mészáros József; Béres Zoltán, Kozma Katalin Abigél, Draskovics József.)
A feladatok sorrendjét illetően bejött a papírforma. Legkönnyebnek az 1. feladat bizonyult (5,44 átlagpontszámmal), de nagy „szakadással”: a 64 versenyző közül 26 ért el 10 pontot és ugyanannyi csupán 1 pontot.
Ismeretes, hogy ![]() Aranyszőrű Tehén
Aranyszőrű Tehén ![]() nap alatt,
nap alatt, ![]() Aranyszőrű Tehén pedig
Aranyszőrű Tehén pedig ![]() nap alatt legelné le a Mesebeli Rét összes füvét. A Mesebeli Réten minden nap ugyanannyi mennyiségű fű nő ki. Hány Aranyszőrű Tehén legelné le a Mesebeli Rét összes füvét
nap alatt legelné le a Mesebeli Rét összes füvét. A Mesebeli Réten minden nap ugyanannyi mennyiségű fű nő ki. Hány Aranyszőrű Tehén legelné le a Mesebeli Rét összes füvét ![]() nap alatt? Hány nap alatt legelné le a Mesebeli Rét összes füvét
nap alatt? Hány nap alatt legelné le a Mesebeli Rét összes füvét ![]() Aranyszőrű Tehén?
Aranyszőrű Tehén?
Kétségtelen, hogy a feladat (amely meseszerű megszövegezésében szövegértési szempontból sem egyszerű) sikertelenségének oka inkább logikai: sokan nem gondoltak arra, hogy a rét nem puszta föld, ott, már eleve van fű. Aki nem vette számításba ezt a fűmennyiséget, a továbbiakban hibátlanul számolva is bajba jutott. A versenyzők általában egyenlettel dolgoztak (lásd javítási útmutató I. megoldás) de volt, aki „józan paraszti ésszel” okoskodott. (Lásd javítási útmutató II. megoldás.)
Legnehezebbnek a 5. feladat bizonyult (pontátlaga 1,92). A 64 versenyző közül mindössze 6 volt, aki 10 pontot ért el, a túlnyomó többség „megijedt”.
Határozza meg az ![]() ,
, ![]() ,
, ![]() valós számok összes értékét, amelyekre
valós számok összes értékét, amelyekre
Alapgondolata (nemnegatív tagok összege csak úgy lehet nulla, ha minden tag az) megvalósításához az algebrai azonosságok virtuóz kezelése (javítási útmutató I. megoldása) vagy a ![]() -ben másodfokú egyenlet diszkrimánsa nemnegatívitásának vizsgálata vezet el. (Lásd javítási útmutató II. megoldása.)
-ben másodfokú egyenlet diszkrimánsa nemnegatívitásának vizsgálata vezet el. (Lásd javítási útmutató II. megoldása.)
A megoldási ötletet további három változatban mutatom be:
III. megoldás. Domokos Ábel (Erdély, Sylvania Kollégium), Hámori Janka (Szeged), Hegedűs Dániel (Budapest), Trombitás Karolina (Pécs), Várkonyi Zsombor (Budapest).
Az
azonos átalakítás után, az
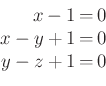
egyenletrendszer megoldása.
IV. megoldás. Sógor Bence (Erdély, Báthory István Elméleti Líceum.)
Az
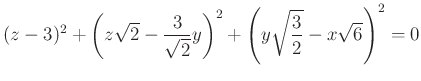
azonos átalakítás után, a
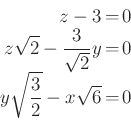
egyenletrendszer megoldása.
V. megoldás. A feladatot beküldő, és egyben javító Kovács Béla tanár úr megoldása:
Az egyenlet mindkét oldalát 2-vel leosztva,
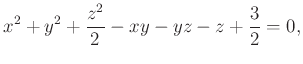
majd az
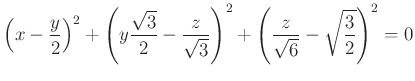
azonos átalakítás után, az
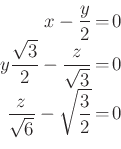
egyenletrendszer megoldása.
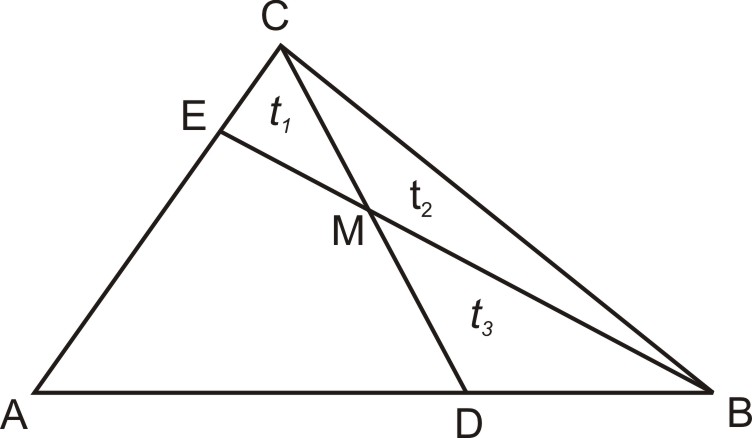
A 6. feladat:
Az ![]() háromszöget két csúcsán átmenő egyenesekkel az ábra szerint három háromszögre és egy négyszögre darabolunk. Mekkora az
háromszöget két csúcsán átmenő egyenesekkel az ábra szerint három háromszögre és egy négyszögre darabolunk. Mekkora az ![]() négyszög területe, ha adottak a háromszögek
négyszög területe, ha adottak a háromszögek ![]() ,
, ![]() és
és ![]() területei?
területei?
A feladat eredményessége (átlagpontszáma 2,73) megfelelt a nehézségi besorolásának. A megoldási útmutató három megoldást is közöl, egyik sem könnyű. Az I. megoldás magva a következő segédtétel:
Tekintve a következő ábrát
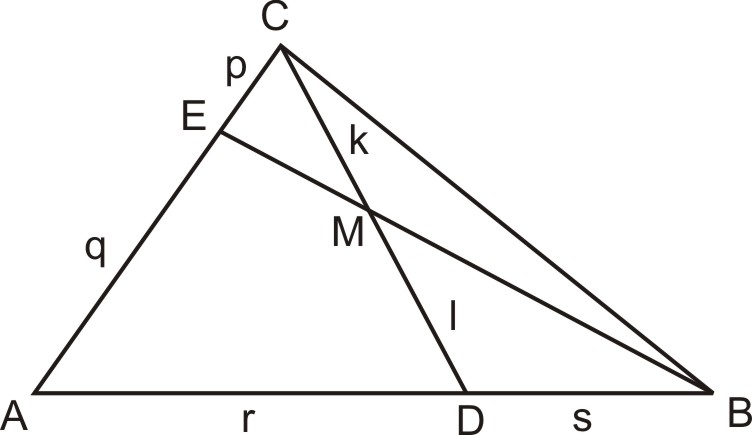
fennáll, hogy
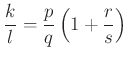
Erre a segédtételre támaszkodva bizonyíthatjuk az (eredeti versenyfeladattól független) tételt:
Az 1. ábra jelöléseit tekintve érvényes, hogy
Bizonyítás: Tekintsük a következő ábrát.
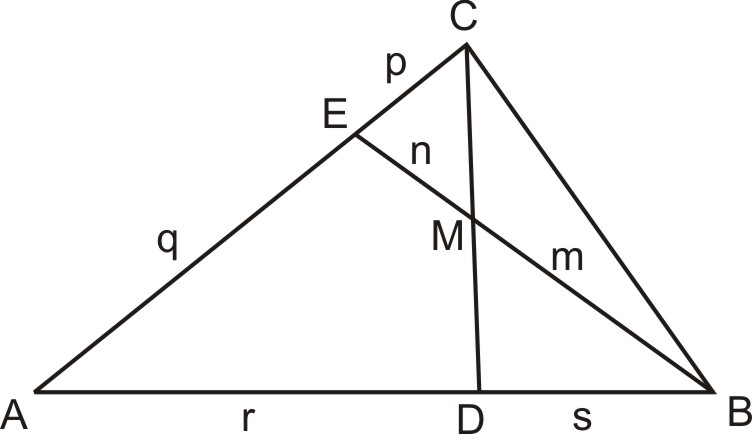
A 2. ábra alapján értelemszerűen fennáll, hogy
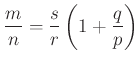
A segédtétel kétszeres alkalmazásával kapjuk, hogy
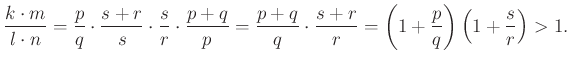
Innen adódik
Jelöljük be az 1. ábra ![]() pontjánál lévő szögeket is!
pontjánál lévő szögeket is!
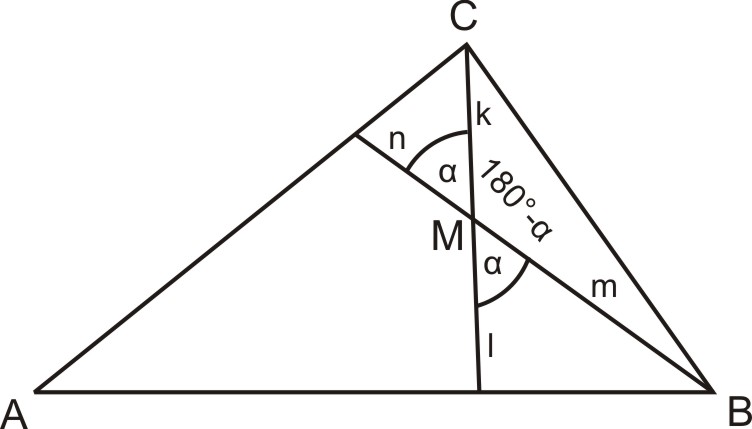
A háromszögekre ismert területképlet alapján

Állításunk akkor és csakis akkor teljesül, ha
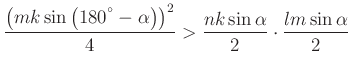
amihez ![]() szükséges és elegendő.
szükséges és elegendő. ![]()
Örvendetes, hogy a 9. évfolyamban akadt egy olyan versenyző is, aki (abszolút győztesként) elérte a maximális 60 pontot: Várkonyi Zsombor. (Budapesti Fazekas Gimnázium. Tanárai: Fazakas Tünde, Kocsis Szilveszter és Pósa Lajos.) Mindössze 2 ponttal maradt mögötte Hámori Janka (Szegedi Radnóti Gimnázium. Tanárai: Schultz János és Tigyi István.) Az első 6 között szerepel két erdélyi diák is: Sógor Bence (Kolozsvár, Báthory István Elméleti Líceum. Tanárai: Nagy Őrs és Kürthy Katalin), Árva Norbert Ákos (Nagyvárad, Ady Endre Elméleti Liceum. Tanára: Báthori Éva). Tizedik helyre futott be Páll László (Beregrákos, Beregszászi Általános Iskola. Tanára: Oljusinec Katalin).
10. évfolyam
(Javító tanárok a feladatok sorrendjében: Turdean Katalin, Egyed László; Remeténé Orvos Viola, Koczinger Éva; Péics Hajnalka, Nemecskó István, Mátéfi István; Básti Angelika, Fonyóné Németh Ildikó, Pálhegyi-Farkas László; Balog Dániel, Kosztolányiné Nagy Erzsébet; Lányi Veronika, Nagy Őrs.)
A feladatokat háromosztatúra terveztük, de nehézségi szintjük végül kétfelé oszlott. (Az első három feladat pontátlaga 7 pont felett volt, az utolsó háromé 3 pont körül mozgott.) Legkönnyebbnek a 2. feladat bizonyult (pontátlaga 8,49), amelyben az ![]() számok pozitív egyjegyű osztóinak számát kellett megtalálni.
számok pozitív egyjegyű osztóinak számát kellett megtalálni.
Már a nehéz csoportba tartozott a 4. feladat (átlagos pontszána 3,29):
Az ![]() négyzet
négyzet ![]() csúcsából húzzunk két olyan félegyenest, amelyek egymással
csúcsából húzzunk két olyan félegyenest, amelyek egymással ![]() -os szöget zárnak be. Az egyik félegyenes a
-os szöget zárnak be. Az egyik félegyenes a ![]() oldalt az
oldalt az ![]() pontban, a
pontban, a ![]() átlót a
átlót a ![]() pontban metszi. A másik a
pontban metszi. A másik a ![]() oldalt az
oldalt az ![]() pontban, a
pontban, a ![]() átlót pedig a
átlót pedig a ![]() pontban metszi. Mutassuk meg, hogy az
pontban metszi. Mutassuk meg, hogy az ![]() háromszög területe kétszerese az
háromszög területe kétszerese az ![]() háromszög területének!
háromszög területének!
Ez egy olyan feladat, aminek a felfogásához elengedhetetlen egy jó ábra. A javítási útmutatóban közölt ötletes megoldás látószögekre, húrnégyszögekre alapoz és valóban eléggé nehéz. A magasabb évfolyamok számára van „fonalas” megoldás is, ami (a kevéssé kedvelt) analitikus geometria módszerére alapoz. Erre lehetőségre az „![]() négyzet” hívja fel a figyelmet. Helyezzünk a négyzetre egy koordináta-rendszert!
négyzet” hívja fel a figyelmet. Helyezzünk a négyzetre egy koordináta-rendszert!
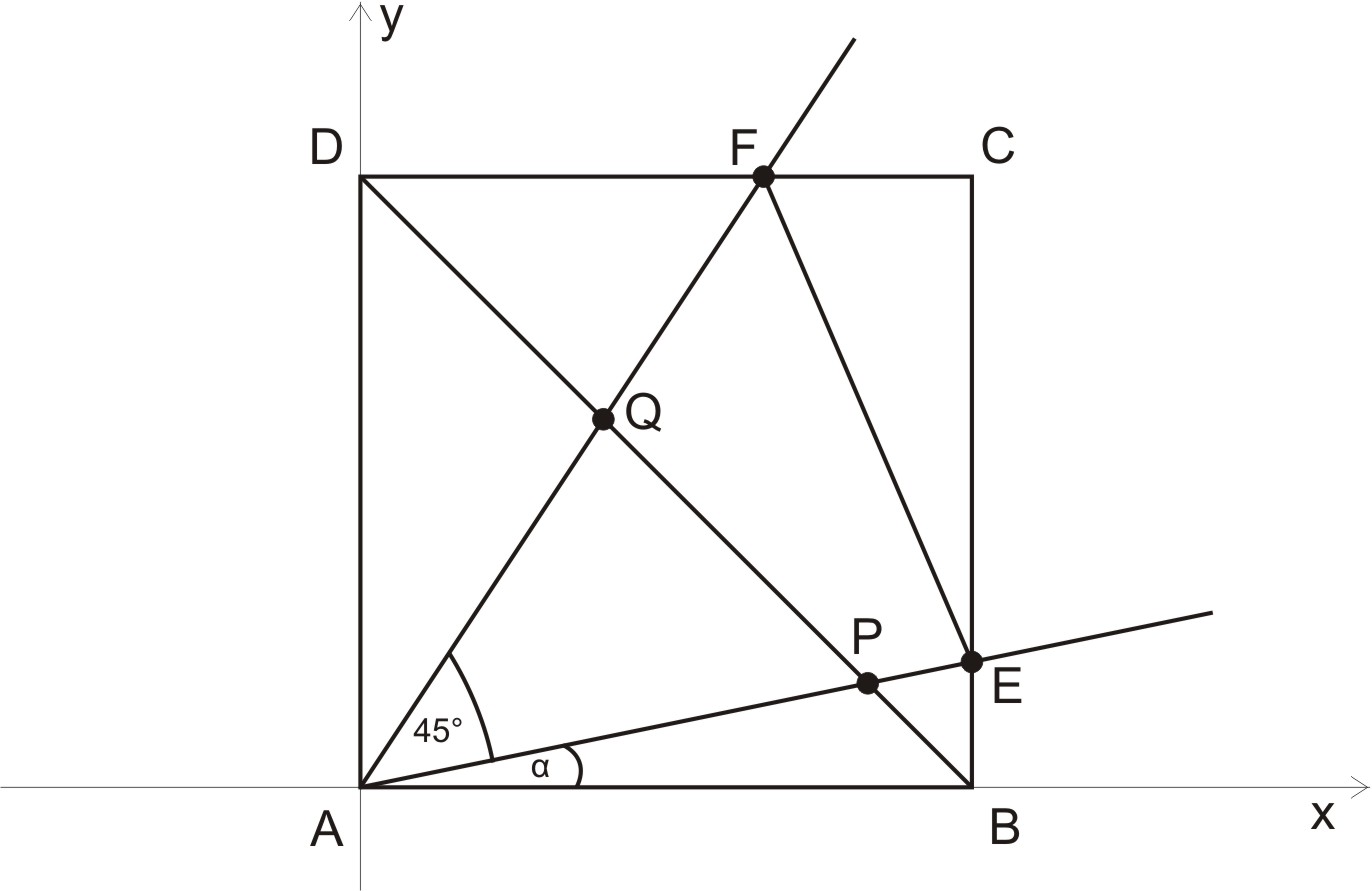
A megoldás stratégiája:
- — Kiszámítjuk a
 ,
, 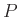 ,
, 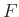 és
és 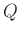 pontok koordinátáit
pontok koordinátáit - — Az
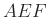 háromszögnél látjuk a négyzetből „levágott” derékszögű háromszögeket.
háromszögnél látjuk a négyzetből „levágott” derékszögű háromszögeket. - — Az
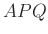 háromszögnél látjuk a
háromszögnél látjuk a 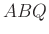 háromszögból „levágott”
háromszögból „levágott” 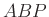 háromszöget.
háromszöget. - — Végül megnézzük: Igaz-e, amit meg kellett mutatnunk?
A stratégia kivitelezése (taktikai fordulatként a négyzetet egységnyi oldalúnak tekintve):
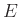 ,
, 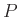 ,
, 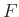 és
és 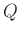 pontok koordinátáinak kiszámítása
pontok koordinátáinak kiszámítása
Ha ![]() vagy
vagy ![]() , a megmutatandó állítás nyilvánvaló. Tegyük fel, hogy
, a megmutatandó állítás nyilvánvaló. Tegyük fel, hogy ![]() .
.
Az ![]() jelöléssel az
jelöléssel az ![]() egyenes egyenlete:
egyenes egyenlete: ![]() , ezért
, ezért ![]() .
.
Az ![]() egyenes iránytényezője
egyenes iránytényezője 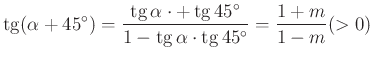 . Ezért az
. Ezért az ![]() egyenes egyenlete
egyenes egyenlete 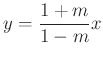 és
és 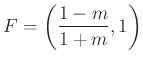 .
.
A ![]() egyenes egyenlete
egyenes egyenlete ![]() . Az
. Az
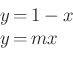
egyenletrendszerből 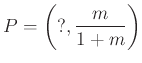 és az
és az
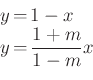
egyenletrendszerből 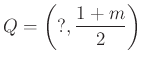 . (A stratégiából látjuk, hogy a
. (A stratégiából látjuk, hogy a ![]() és
és ![]() pontok abszcisszáira nem lesz szükségünk.)
pontok abszcisszáira nem lesz szükségünk.)
Az  háromszög területének kiszámítása
háromszög területének kiszámítása
Az ![]() négyzet területe 1 (területegység, a továbbiakban nem említjük).
négyzet területe 1 (területegység, a továbbiakban nem említjük).
Az ![]() háromszög területe
háromszög területe ![]() , az
, az ![]() háromszög területe
háromszög területe 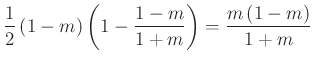 és az
és az ![]() háromszög területe
háromszög területe 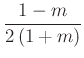 . Ezért az
. Ezért az ![]() háromszög területe
háromszög területe
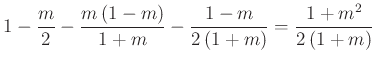 .
.Az ![]() háromszög területének kiszámítása
háromszög területének kiszámítása
Az ![]() háromszög területe
háromszög területe 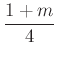 , az
, az ![]() háromszög területe
háromszög területe 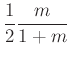 , ezért az
, ezért az ![]() háromszög területe
háromszög területe
 .
.Az ![]() háromszög területe az
háromszög területe az ![]() háromszög területének kétszerese.
háromszög területének kétszerese. ![]()
A 6. feladat bizonyult a legnehezebbnek (átlagpontszám 2,97):
Egy egyenlő szárú ![]() háromszög
háromszög ![]() alapjának belső
alapjának belső ![]() pontján keresztül párhuzamosokat húzunk a szárakkal. Ezek a párhuzamosok az
pontján keresztül párhuzamosokat húzunk a szárakkal. Ezek a párhuzamosok az ![]() -t az
-t az ![]() pontban, az
pontban, az ![]() -t a
-t a ![]() pontban metszik. Bizonyítandó, hogy a
pontban metszik. Bizonyítandó, hogy a ![]() pont
pont ![]() egyenesre vonatkozó tükörképe az egyenlő szárú háromszög köré írt körön van.
egyenesre vonatkozó tükörképe az egyenlő szárú háromszög köré írt körön van.
„Természetesen” ennek is van analitikus geometriai megoldása, de ez egy verseny időtartama alatt aligha fejezhető be: Még egy olyan koordináta-rendszerben is, ahol a ![]() alap az „
alap az „![]() tengely”
tengely” ![]() intervalluma, a csúcspont
intervalluma, a csúcspont ![]() , a háromszög köré írt kör középpontjára
, a háromszög köré írt kör középpontjára 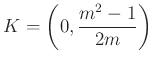 , sugarára
, sugarára 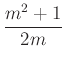 adódik. A
adódik. A ![]() tetszőleges belső pont esetén, ennek a
tetszőleges belső pont esetén, ennek a ![]() egyenesre vonatkozó tükörképe
egyenesre vonatkozó tükörképe
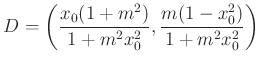 .
.A bizonyításhoz ki kell mutatni, hogy ![]() -tól függetlenül
-tól függetlenül 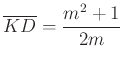 . („Drága” 10 pontot szerez, aki ezt végigcsinálja.)
. („Drága” 10 pontot szerez, aki ezt végigcsinálja.)
Érdekesen alakult ennek a feladatnak az utóélete. Beküldője, Laczkó László tanár úr nem volt megelégedve saját (a javítási útmutatóban közölt) megoldásával, ezért utólag még két megoldást küldött a zsűrinek, amelyeket az alábbiakban mutatunk be. Megismételjük a javítási útmutatóban lévő megoldásban szereplő ábrát, amelyen a ![]() pontnak a
pontnak a ![]() egyenesre vonatkozó tükörképe a
egyenesre vonatkozó tükörképe a ![]() pont.
pont.
II. megoldás.
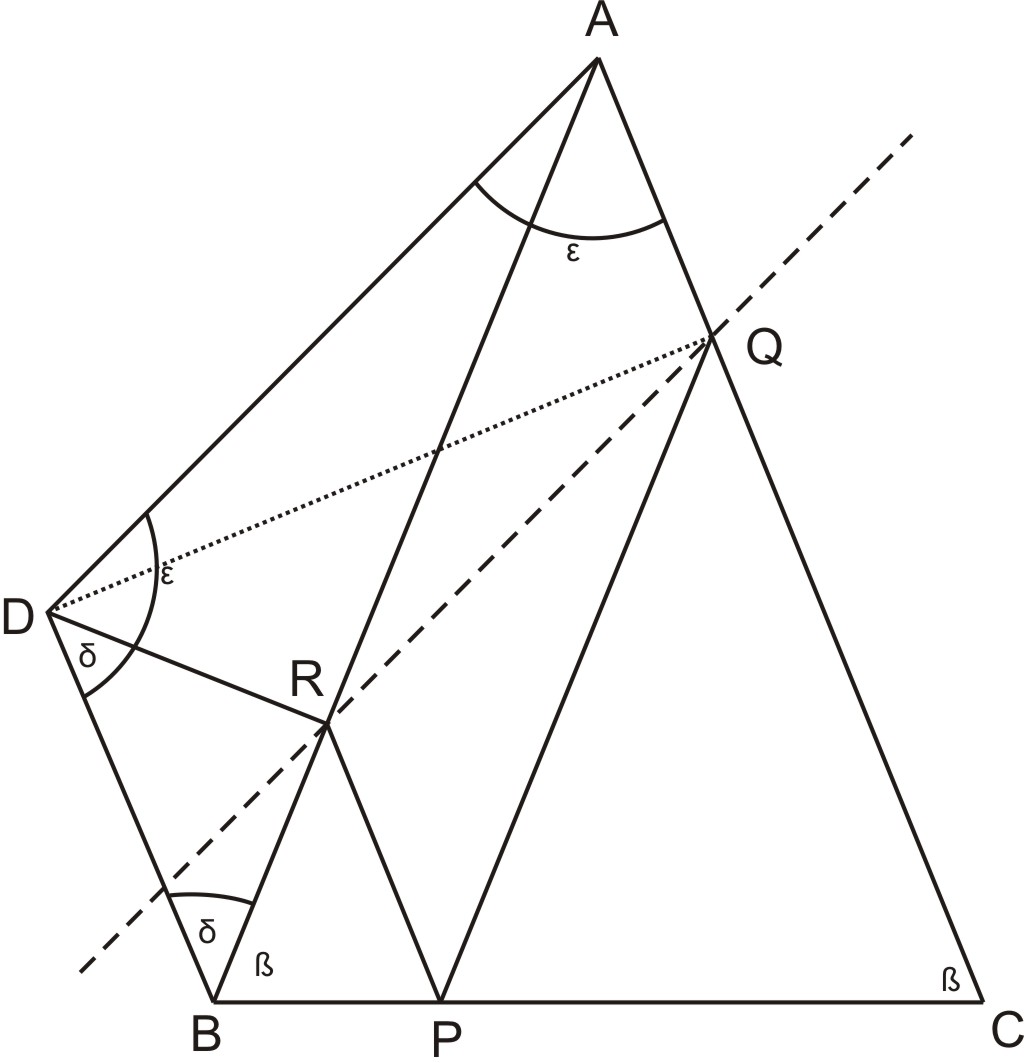
Elég belátni, hogy az ![]() és
és ![]() pontokból a
pontokból a ![]() szakasz ugyanakkora szög alatt látszik.
szakasz ugyanakkora szög alatt látszik.
Mivel ![]() , ezért a
, ezért a ![]() ,
, ![]() és
és ![]() pontok rajta vannak egy
pontok rajta vannak egy ![]() középpontú körön. A kerületi és középponti szögek tétele értelmében
középpontú körön. A kerületi és középponti szögek tétele értelmében 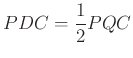 .
.
Mivel ![]() , ezért a
, ezért a ![]() ,
, ![]() és
és ![]() pontok rajta vannak egy
pontok rajta vannak egy ![]() középpontú körön. A kerületi és középponti szögek tétele értelmében
középpontú körön. A kerületi és középponti szögek tétele értelmében 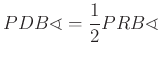 . Így
. Így
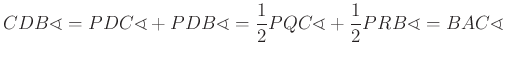
Ezzel beláttuk, hogy a ![]() szakasz az
szakasz az ![]() és
és ![]() pontokból ugyanakkora szög alatt látszik.
pontokból ugyanakkora szög alatt látszik. ![]()
III. megoldás.
A 6. ábra mutatja, hogy az ![]() és
és ![]() háromszögek egybevágóak. (Megfelelő oldalaik egyenlő hosszúak.) Emiatt az
háromszögek egybevágóak. (Megfelelő oldalaik egyenlő hosszúak.) Emiatt az ![]() négyszög szimmetrikus trapéz. Ezért a
négyszög szimmetrikus trapéz. Ezért a ![]() pont az
pont az ![]() pontnak a trapéz szimmetriatengelyére vonatkozó tükörképe.
pontnak a trapéz szimmetriatengelyére vonatkozó tükörképe.
Legyen ![]() az
az ![]() háromszög köré írható kör középpontja. Ha
háromszög köré írható kör középpontja. Ha ![]() körül az
körül az ![]() húrt a
húrt a ![]() húrba forgatjuk (
húrba forgatjuk (![]() kerül a
kerül a ![]() -be és
-be és ![]() kerül az
kerül az ![]() -ba), akkor
-ba), akkor ![]() miatt, az
miatt, az ![]() pont a
pont a ![]() -ba fordul. Ezért a
-ba fordul. Ezért a ![]() és
és ![]() pontok egyenlő távol vannak az
pontok egyenlő távol vannak az ![]() ponttól. Szakaszfelező merőlegesük a trapéz szimmetriatengelye, amely tartalmazza az
ponttól. Szakaszfelező merőlegesük a trapéz szimmetriatengelye, amely tartalmazza az ![]() pontot. Ezek szerint a trapéz szimmetriatengelye az
pontot. Ezek szerint a trapéz szimmetriatengelye az ![]() háromszög köré írható kör átmérőjének egyenese.
háromszög köré írható kör átmérőjének egyenese.
„Segédtételként” felhasználjuk, hogy ha egy kör kerületének egy pontját egyenesre tükrözzük, a tükörkép akkor és csakis akkor esik ismét a körre, ha az egyenes a kör valamelyik átmérőjének egyenese. Mivel a ![]() pont az
pont az ![]() pontnak a trapéz szimmetriatengelyére vonatkozó tükörképe és az
pontnak a trapéz szimmetriatengelyére vonatkozó tükörképe és az ![]() pont rajta van az
pont rajta van az ![]() középpontú körön, a
középpontú körön, a ![]() pontnak szükségképpen rajta kell lenni az
pontnak szükségképpen rajta kell lenni az ![]() háromszög köré írható körön.
háromszög köré írható körön. ![]()
Dicséretes, hogy a 10. évfolyam (63 versenyzőből álló) mezőnyéből a hat főből álló élmezőnyben a 6. feladatra mindenki 10 pontot kapott. Az első helyezett lett 58 ponttal Jánosik Áron (Győr, Révai Gimnázium. Tanárai: Csete Lajos és Árki Tamás). 53 ponttal határon túli a harmadik-negyedik helyezett Miklós Csenge (Sepsiszentgyörgy, Székely Mikó Kollégium. Tanára: Ugron Szabolcs). Ugyanennyi pontot szerzett Weisz Máté (Szegedi Radnóti Gimnázium. Tanárai: Schultz János és Tigyi István).
A tanár és tanárjelölt kollégák figyelmébe ajánlható a 10. évfolyam 1. feladata, amely fokozatosan nehezíthető: kezdetben akár következetesen gondolkodó általános iskolások is megoldhatják, később hasznossá válnak a kombinatorika alapjai.
A nyári festőtáborban a gyerekek ecseteket és a tisztításukhoz szükséges anyagokat, rajzlapokat és festékgombokat kapnak, amelyekből tetszés szerint válogatva az alapszínek mellett mindig új keverékszínekhez jutnak. Minden alap- illetve keverékszínt külön rajzlapon próbálnak ki. Gyerekenként legalább hány rajzlapra van szükség, ha egy a válogatásban kiszemelt festékgomb csak legfeljebb egyszer és ugyanakkora mennyiségben szerepel feltéve, hogy a festékgombok színei: piros, kék, sárga és zöld?
Megoldás.
A tanár számára a válasz, a hatványhalmaz számosságára vonatkozó ismeret vagy a  (az üres halmazt kihagyjuk) képlet alapján, azonnali. Az eredeti feladat a diák számára is könnyű. (Ennek ellenére figyelemre méltó, hogy a versenyzők 20%-a ennél a feladatnál 1 pontot kapott.)
(az üres halmazt kihagyjuk) képlet alapján, azonnali. Az eredeti feladat a diák számára is könnyű. (Ennek ellenére figyelemre méltó, hogy a versenyzők 20%-a ennél a feladatnál 1 pontot kapott.)
Öt festék, azaz ![]() esetén az
esetén az 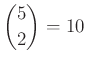 kombinatorika nélkül, például: egy (konvex) ötszög oldalainak és átlóinak száma. Ötlet segít az
kombinatorika nélkül, például: egy (konvex) ötszög oldalainak és átlóinak száma. Ötlet segít az ![]() kiszámolásához: Ha 5 pontból 3 pontot kiválasztva, kimarad 2 pont, ezért
kiszámolásához: Ha 5 pontból 3 pontot kiválasztva, kimarad 2 pont, ezért 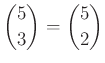 . (Végeredmény: 31.)
. (Végeredmény: 31.)
6 festék, azaz ![]() esetén a
esetén a ![]() kombinatorika nélkül kiszámítva: 6 pontból egy pontot rögzítünk. A többi öt pontból kiválasztható ponthármasok száma
kombinatorika nélkül kiszámítva: 6 pontból egy pontot rögzítünk. A többi öt pontból kiválasztható ponthármasok száma ![]() már ismert az előzőekből. Ezekhez még hozzá kell venni azokat a ponthármasokat, amelyekben a rögzített ponthoz még 2 pontot veszünk a többiből. Ezek száma
már ismert az előzőekből. Ezekhez még hozzá kell venni azokat a ponthármasokat, amelyekben a rögzített ponthoz még 2 pontot veszünk a többiből. Ezek száma ![]() . Így
. Így  . (Végeredmény:
. (Végeredmény: ![]() .)
.) ![]()
11. évfolyam
(Javító tanárok a feladatok sorrendjében: Györke Róbert, Dr. Kántor Sándorné; Deák Éva, Udvaros József, Dr. Kántor Sándor; Ágó Balog Krisztina, Kovács Lajos, Liska Zsanett; Erdős Gábor, Vistan Laura; Kallós Béla, Ugron Szabolcs, Szigeti Tamás; Hodgyai Edit, Gálné Groma Virág, Trembeczky Csaba.)
Ezúttal a 2. feladat okozott meglepetést:
Az ![]() hegyesszögű háromszögben
hegyesszögű háromszögben ![]() . Legyen
. Legyen ![]() az
az ![]() csúcsból húzott magasság talppontja a
csúcsból húzott magasság talppontja a ![]() oldalon,
oldalon, ![]() és
és ![]() az
az ![]() és
és ![]() oldalak pontjai, úgy, hogy
oldalak pontjai, úgy, hogy ![]() és
és ![]() .
.
a) Igazoljuk, hogy a ![]() négyszög húrnégyszög!
négyszög húrnégyszög!
b) Mekkora az ![]() és
és ![]() háromszögek területének aránya?
háromszögek területének aránya?
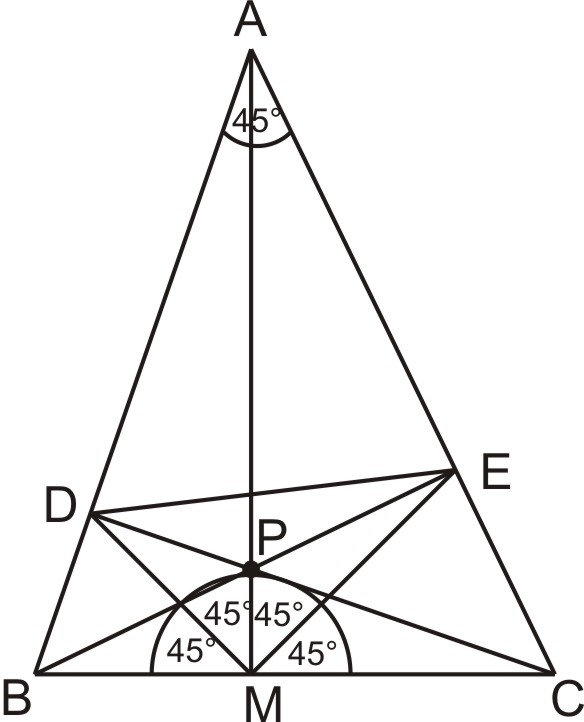
Különösen a b) rész bizonyult nehéznek, mert a megoldás az a) rész eredményére támaszkodik. (A javítási útmutató az a) részre két megoldást, a b) részre egy megoldást közöl.) A feladatra kapott pontszámok átlaga: 3,88. A 63 fős mezőnyben csupán 6 versenyző érte el a 10 pontot.
Úgy látszik, a geometria az oktatási folyamat „leggyengébb láncszeme”, amit példáz a (zsűri által is legnehezebbnek tartott) 6. feladat:
Az ![]() téglalapba írjunk
téglalapba írjunk ![]() szabályos háromszöget úgy, hogy az
szabályos háromszöget úgy, hogy az ![]() pont a
pont a ![]() , az
, az ![]() pont a
pont a ![]() oldal belső pontja.
oldal belső pontja.
a) A téglalap ![]() és
és ![]() oldalainak milyen
oldalainak milyen ![]() arányánál lehet a téglalapba a fentiek szerint szabályos háromszöget írni?
arányánál lehet a téglalapba a fentiek szerint szabályos háromszöget írni?
b) Bizonyítsuk be, hogy az ![]() ,
, ![]() és
és ![]() háromszögek területének egyike a két másik háromszög területének összegével egyenlő!
háromszögek területének egyike a két másik háromszög területének összegével egyenlő!
A feladat pontátlaga 3,65 pont, 10 pontot 5 versenyző ért el. A javítási útmutató az a) részre egy forgatáson alapuló megoldást közöl, amelyre kevesen jöttek rá. „Mentőkötél” volt viszont, — feltételezve azt, hogy a téglalap olyan, hogy bele az a) rész kívánalmainak megfelelő szabályos háromszög írható — a b) részben kért bizonyítás kivitelezhető. (Emiatt a versenyzők mintegy harmada szerzett 5—9 közötti pontot.) A javítási útmutató a b) részre két megoldást közöl. A második a trigonometrián alapul. Pótlólag szerepeljen itt, az a) résznek trigonometria segítségével adódó megoldása: A szabályos háromszög beírhatóságának szükséges és elegendő feltétele a következő ábra érvényessége.
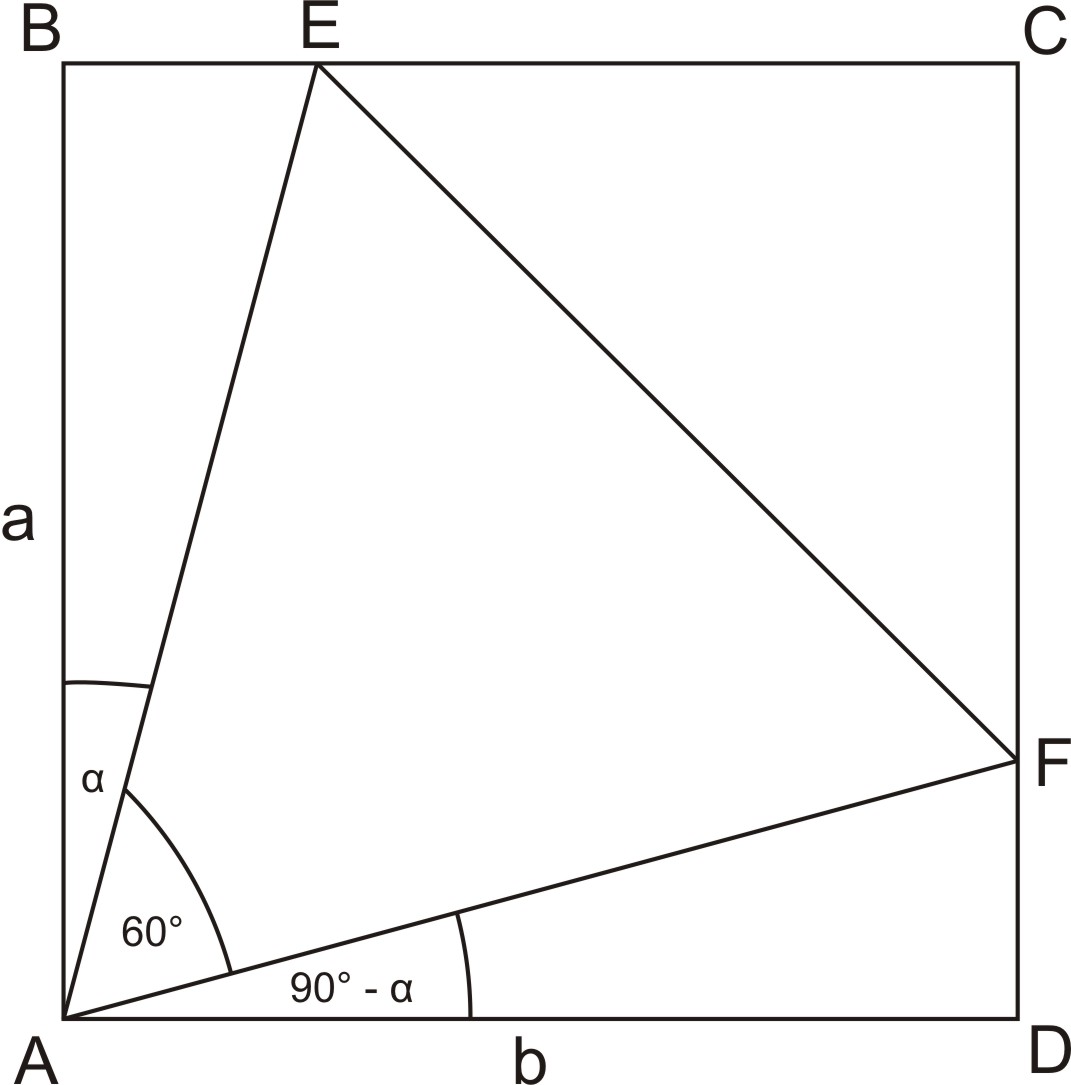
Mivel az ![]() pont a
pont a ![]() , az
, az ![]() pont a
pont a ![]() oldal belső pontja,
oldal belső pontja, ![]() . Az
. Az ![]() háromszög akkor és csak akkor szabályos, ha
háromszög akkor és csak akkor szabályos, ha

Innen a trigonometrikus azonosságok felhasználásával, ekvivalens átalakítással adódik
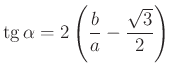 .
.Mivel 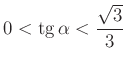 , ezért
, ezért  , amiből megkapjuk, hogy a téglalapba a szabályos háromszög akkor és csak akkor írható, ha
, amiből megkapjuk, hogy a téglalapba a szabályos háromszög akkor és csak akkor írható, ha
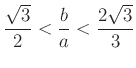 .
. A 11. évfolyam első helyezettje 57 ponttal Szabó Kristóf (Budapesti Fazekas Gimnázium. Tanárai: Dobos Sándor, Kiss Gergely és Kiss Géza). Őt csupán 1 ponttal lemaradva hárman is követték: Pituk Gábor (Lovassy László Gimnázium. Tanárai: Katanics Sándor és Böcskei Ákos), Póta Balázs (Győr, Révai Gimnázium. Tanárai: Árki Csilla és Árki Tamás.), Schrettner Jakab (Szegedi Radnóti Gimnázium. Tanárai: Mike János és Schultz János) 53 pontot ért el Ferencz Dániel (Marosvásárhely, Bolyai Farkas Elméleti Liceum. Tanára: Mátéfi István), 50 pontos lett Fazakas Borbála (Kolozsvár, Báthory István Elméleti Liceum. Tanára: Szilágyi Judit). Két-három ponttal mögöttük Szögi Roland (Zenta, Bolyai Tehetséggondozó Gimnázium és Kollégium. Tanárai: Ágó Balog Krisztina, Ripcó Sipos Elvira és Kaszás Botos Zsófia) és Portik Abel (Szováta, Domokos Kázmér Iskolacsoport. Tanára: Portik Antal). Három 46 pontos zárja a díjazottak névsorát: Dékány Barnabás (Pécs, Janus Pannonius Gimnázium. Tanárai: Meiszterics Zoltánné és Lehőcz Mária), Péter István (Csíkszereda, Márton Áron Főgimnázium. Tanára: Tamási Csaba), Sulan Ádám (Nagykanizsa, Batthyány Lajos Gimnázium. Tanárai: Erdős Gábor és Erdősné Németh Ágnes).
12. évfolyam
(Javító tanárok a feladatok sorrendjében: Horváth Katalin, Pall Olga, Veres Pál; Fedorszkí Ádám, Marczis György; Pálovicsné Tusnády Katalin, Péter András; Dávid Géza, Kicska György, Lakatosné Weszelovszki Éva; Dr. Kiss Géza, Kekenák Tamás; Bíró Bálint, Bíró Zoltán, Ruffné Szakály Zsuzsanna.)
Az indulók száma itt volt a legkisebb, 43 fő. (Ez magyarázható azzal, hogy több, tavalyi 11. évfolyamos már érettségire, esetleg nem matematika felvételire készült.)
Könnyűnek találtatott a 4. feladat: Egy pénzérmét feldobunk egymás után 10-szer. Mennyi a valószínűsége annak, hogy nem lesz két egymást követő fej ebben a sorozatban? (Pontátlag: 7,02.)
Megoldás.
Igazolható az ![]() hosszúságú, két egymást követő fejet nem tartalmazó dobássorozatok
hosszúságú, két egymást követő fejet nem tartalmazó dobássorozatok ![]() számára az
számára az ![]() rekurzív összefüggés, ahol
rekurzív összefüggés, ahol ![]() (írás, fej),
(írás, fej), ![]() (írás—írás,írás—fej,fej—írás). A valószínűségszámítás szempontjából „kedvező eset”
(írás—írás,írás—fej,fej—írás). A valószínűségszámítás szempontjából „kedvező eset” ![]() számát megkapjuk ezzel a rekurzív képzési szabállyal. Mivel az „összes eset” száma
számát megkapjuk ezzel a rekurzív képzési szabállyal. Mivel az „összes eset” száma ![]() , a keresett valószínűség
, a keresett valószínűség 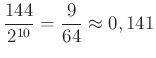 .
. ![]()
Ebből a feladatból általánosítással egyetemi szintű feladat kerekedik:
Egy pénzérmét feldobunk egymás után ![]() -szer. Mennyi a valószínűsége annak, hogy nem lesz két egymást követő fej ebben a sorozatban? Van-e határértéke ennek a valószínűségnek, ha a dobások száma minden határon túl nő?
-szer. Mennyi a valószínűsége annak, hogy nem lesz két egymást követő fej ebben a sorozatban? Van-e határértéke ennek a valószínűségnek, ha a dobások száma minden határon túl nő?
Megoldás.
A megoldás során kénytelenek vagyunk a rekurzív (Fibonacci-típusú) ![]() sorozatot
sorozatot ![]() indulással
indulással

alakban felírni, ami után a keresett valószínűség
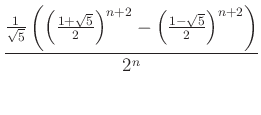
(Ellenőrizhető, ![]() esetén kapjuk a korábbi eredményt.)
esetén kapjuk a korábbi eredményt.)
Az
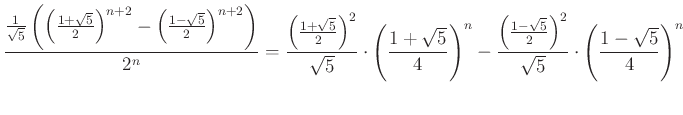
felbontás után a  és
és 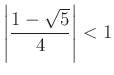 miatt a második kérdésre is választ kapunk:
miatt a második kérdésre is választ kapunk:
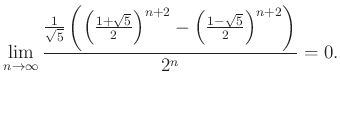
Igazi kihívást jelentett az 5. feladat:
Adott a ![]() nem-negatív egész szám és
nem-negatív egész szám és ![]() sorozat, ahol
sorozat, ahol ![]() , és minden
, és minden ![]() -re
-re
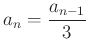 , ha
, ha ![]() osztható 3-mal;
osztható 3-mal;
![]() , ha
, ha ![]() nem osztható 3-mal.
nem osztható 3-mal.
Keressük meg az összes olyan ![]() számot, amelyre érvényes, hogy létezik olyan
számot, amelyre érvényes, hogy létezik olyan ![]() természetes szám, amelyre
természetes szám, amelyre ![]() .
.
Arra még könnyű volt rájönni, hogy ![]() esetén a sorozat minden tagja 1, ezért már
esetén a sorozat minden tagja 1, ezért már ![]() . A
. A ![]() ,
, ![]() esetén
esetén ![]() ,
, ![]() , ... mutatja, hogy az
, ... mutatja, hogy az ![]() sorozat szigorúan növekedő, tehát ilyen esetekben a keresett
sorozat szigorúan növekedő, tehát ilyen esetekben a keresett ![]() nem létezik. De mi van a többi esetben? Próbálgassunk!
nem létezik. De mi van a többi esetben? Próbálgassunk!
![]() esetben az
esetben az ![]() sorozat kezdete: 1, 2, 3, 1..., tehát
sorozat kezdete: 1, 2, 3, 1..., tehát ![]() .
.
![]() esetben az
esetben az ![]() sorozat kezdete: 1, 3, 1..., tehát
sorozat kezdete: 1, 3, 1..., tehát ![]() .
.
![]() esetben az
esetben az ![]() sorozat kezdete: 1, 5, 9, 3, 1..., tehát
sorozat kezdete: 1, 5, 9, 3, 1..., tehát ![]() .
.
![]() esetben az
esetben az ![]() sorozat kezdete: 1, 6, 2, 7, 12, 4, 9, 3 ,1..., tehát
sorozat kezdete: 1, 6, 2, 7, 12, 4, 9, 3 ,1..., tehát ![]() .
.
![]() esetben az
esetben az ![]() sorozat kezdete: 1, 8, 15, 5, 12, 4, 11, 18, 6, 2, 9, 3, 1;
sorozat kezdete: 1, 8, 15, 5, 12, 4, 11, 18, 6, 2, 9, 3, 1; ![]() .
.
![]() esetben az
esetben az ![]() sorozat kezdete: 1, 9, 3, 1..., tehát
sorozat kezdete: 1, 9, 3, 1..., tehát ![]() .
.
Látjuk, hogy ezekben az esetekben az ![]() sorozat periodikus. Sejtésünk az, hogy a
sorozat periodikus. Sejtésünk az, hogy a ![]() és a 3-mal nem osztható pozitív egészek a feladat megoldásai. E sejtés bizonyításáig még hosszú út vezet. Az elszánt Olvasó két utat is talál a javítási útmutatóban, a 12. évfolyam 5. feladatára adott megoldásban. A döntő többségnek a bizonyítás meghaladta erejét. (Átlagpontszám 3,38.)
és a 3-mal nem osztható pozitív egészek a feladat megoldásai. E sejtés bizonyításáig még hosszú út vezet. Az elszánt Olvasó két utat is talál a javítási útmutatóban, a 12. évfolyam 5. feladatára adott megoldásban. A döntő többségnek a bizonyítás meghaladta erejét. (Átlagpontszám 3,38.)
Nem véletlen, hogy csak három versenyző ért el 10 pontot: Simon Dániel Gábor (Kecskeméti Bányai Julia Gimnázium. Tanárai: Varga József, Pósa Lajos, Szűcs Gábor és Dobos Sándor), Záhorszky Ákos (Ipolyság, Szondy György Gimnázium. Tanárai: Gajdács Mónika, Hujter Bálint és Gyenes Zoltán) mindketten idei Urbán János Díjasok, és Gáspár Attila (Miskolc, Földes Ferenc Gimnázium. Tanárai: Gulyás Tibor és Győry Ákos), aki a korábbi Urbán János Díjasok egyike. (A tavalyi Urbán János Díjas Vistanova, Laura nevét már a versenyfeladatokat javasló kollégák felsorolásában láthattuk.)
A 6. Feladat:
Oldjuk meg a valós számok halmazán a
egyenletet!
A versenyzők a várt 5,4 átlagpontszámot hozták, de Csuha Boglárka (Keszthely, Vajda János Gimnázium. Tanára: Fonyóné Németh Ildikó), Németh Ciprián (Zalaegerszeg, Zrínyi Miklós Gimnázium. Tanára: Kiss Zsolt) és Szemerédi Levente (Szegedi Radnóti Gimnázium. Tanárai: Schultz János és Tigyi István) megtalálták a javítási útmutatóban közölt öt (!) megoldás közül a legszebbet (ez, persze, szubjektív megítélés) és ezért a zsűri különdíját kapták.
Megoldás. (A három versenyző hasonló logikájú munkájának összevonása.)
Rendezzük át az egyenletet és utána mindkét oldalt emeljük köbre!
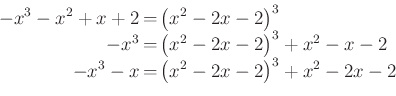
ekvivalens átalakítások után legyen ![]() és
és ![]() . Ekkor
. Ekkor
Tekintve az ![]() ;
; ![]() függvény szigorú monotonitását (a versenyzők ezt nem indokolták, de ezen a szinten triviálisnak vehető), az előbbi egyenlőség akkor és csak akkor teljesülhet, ha
függvény szigorú monotonitását (a versenyzők ezt nem indokolták, de ezen a szinten triviálisnak vehető), az előbbi egyenlőség akkor és csak akkor teljesülhet, ha
Emiatt, az eredeti egyenlet megoldásai pontosan a
másodfokú egyenlet gyökei, ![]() és
és ![]() . (Volt, aki a „biztonság kedvéért” az eredeti egyenletbe való behelyettesítéssel a próbát is elvégezte.)
. (Volt, aki a „biztonság kedvéért” az eredeti egyenletbe való behelyettesítéssel a próbát is elvégezte.) ![]()
A kiváló eredményt elérő versenyzőket többé-kevésbé már említettük, de a teljesség kedvéért felsoroljuk a szép eredményeket felmutató többi díjazottat is: 52—54 pont között teljesített Busa Máté (Nagykanizsa, Batthyány Lajos Gimnázium. Tanárai: Erdős Gábor és Erdősné Németh Ágnes), Daróczi Sándor (Nyíregyháza, Krúdy Gyula Gimnázium. Tanárai: Dr. Kiss Sándor és Konczné Végh Leona) és Kassai Levente (Szegedi Radnóti Gimnázium. Tanárai: Tigyi István, Szaszkó-Bogárné Eckert Bernadett és Schultz János). 47—50 pont között teljesített Schifferer András (Kaposvári Táncsics Mihály Gimnázium. Tanárai: Biczóné Lengyel Beáta és Szigeti Tamás) és Szinyéri Bence (Nagykanizsa, Batthyány Lajos Gimnázium. Tanárai: Erdős Gábor és Erdősné Németh Ágnes).
Biztatásul, az idei 11. évfolyam számára kiemelhető, hogy az idei (12. évfolyamos) Urbán János Díjasok — pontszámaikat tekintve — túlszárnyalták a tavalyi, XXVI. Nemzetközi Magyar Matematikaversenyen (amiről nagyon szép kiadványt jelentetett meg a somorjai Madách Imre Gimnázium Pro Ratio Alapítványa) elért eredményeiket: Az idén Simon Dániel Gábor 60 pontos lett és Záhorszky Ákos 10%-ot javított a tavalyi pontszámán. A tavalyi 11. évfolyamosok élmezőnyéből többen (Busa Máté, Daróczi Sándor, Kassai Levente) az idén is, immár a 12. évfolyamon, az élbolyban maradtak.
Még egy-két sor a zsűri „közérzetéről”: Kiválóan szervezett, jó hangulatú, zavarmentes és kellemes, külön programokkal ellátott versenyen vettünk részt, hála a Kaposvári Táncsics Mihály Gimnáziumnak és Kollégiumának, Kaposvár Megyei Jogú Városnak, különösen a főszervező Tóthné Berzsán Gabriella igazgatóhelyettes asszonynak és fő segítőjének, Kubatov Antal tanár úrnak.