A számok titkos élete

Kate Kitagawa és Timothy Revell: A számok titkos élete: A matematika ismeretlen úttörőinek története, 2024, Corvina 328. o. fordította Szegedi Péter.

A matematika sokak által rettegett tantárgy. A matematika népszerűsítésének egyik lehetősége a matematikatörténeten keresztül vezet. A jelen könyv minél szélesebb olvasókört akar meghódítani a matematikatörténetnek, ezért is üdvözlendő magyar kiadása. Kevés képlet, sok ábra, érdekes történetek. A borító hátán levő szöveg világosan elárulja: a könyv nemcsak a matematika ismeretlen úttörőiről, hanem elsősorban olyan jelentős matematikusokról szól, akiket a fehér férfiak sokáig elnyomtak: tehát nőkről, ázsiaiakról és feketékről. A recenzió írója matematikus végzettségű műkedvelő matematikatörténész, aki maga is írt matematikatörténetet (Simonovits, 2009), de azt felsőfokú matematikai képzettségű olvasóknak szánta. Ez a könyv sokkal szélesebb körnek szól, és reménykedem, hogy olyan emberek érdeklődését is felkelti a matematika története és maga a matematika iránt, akik eddig nem érdeklődtek irántuk.

Két részre osztom a recenziót: ami tetszett és ami nem.

Ami tetszett

A szerzők megpróbálnak az őskorból a legújabb korig eljutni.

A legrégebbi felfedezések sok ezer évesek, a legújabbak pedig 2000 körüliek. A szerzők világosan érzékeltetik, hogy már az ősember is foglalkozott matematikával, és még ma sem zárult le a matematika fejlődése. A milleniumi díjak listáján szereplő problémák közül például ábrapárral mutatja be a Poincaré-sejtést, és ennek kapcsán vázolja a különc megoldó, Perelman életét (aki nemcsak az 1 millió dolláros díjat, de a Fields-érmet sem vette át). Még a mindennapjainkba ma behatoló mesterséges intelligencia matematikai problémáit is érintik.

Nem szorítkoznak a nagy európai civilizációban élő férfi matematikusokra. Természetesen sok neves fehér férfi matematikussal találkozunk ebben a könyvben is. Részletesen megismerkedünk Eukleidész (i.e. 3. század Alexandria) axiomatikus geometriájával, Cardano (Milano, 1550 körül) szerencsejátékaival, Descartes (francia, 17. század első fele) analitikus geometriájával, az angol Newton és a német Leibniz kalkulusával (1700 körül). Találkozunk a matematikusok fejedelmével, Gauss-szal (Göttingen, 19. század első fele). Megemlíthetjük még Hilbertet, aki 1900-ban megfogalmazta az akkori matematika 23 megoldatlan feladatkörét. De a szerzőket elsősorban a nevezettek mögött rejlő ismeretlen matematikusok érdeklik. Kezdjük először a nőkkel.

Alexandriában élt az egyik első női matematikus, Hüpatia (4. század második fele), aki kommentárokat fűzött Diophantosz és Ptolemaiosz ókori csillagász műveihez. Jó gyakorlati érzéke lehetett, mert hathatósan segített egy tanítványának csillagászati segédeszközöket készíteni. Egy politikai válságban meggyilkolták (3. fejezet: Egy Alex nevű város).

Színre lép Descartes is, akit legtöbben az analitikus geometria atyjaként ismernek. Neves szellemi vitapartnere Erzsébet hercegnő volt, akinek apja Csehország „téli” királya volt 1620-ban. A hercegnő száműzetésben Hágában élt és ott találkozott Descartes-tal, egyebek között Apollóniosz körszerkesztési feladatait vitatták meg (7. fejezet. A lehetetlen álom).

Már az előszóban megjelenik Weierstrass kedvenc női tanítványa, Kovalevszkája magánéletét és matematikai tevékenységét egyaránt bőségesen tárgyalja a könyv (11. fejezet. A matematikai hableány). Matematikai munkássága elég nehezen népszerűsíthető, érthető, hogy több teret kapott viharos magánélete. De a 210. oldalon szereplő pörgettyűk közérthetően ábrázolják a hősnő vizsgálati területét.

Meglepő a 9. fejezet (Newtonizmus hölgyeknek). A fejezet először nagyon érthetően összefoglalja a Keplertől Newtonig terjedő fejlődést, amely megmagyarázta a Naprendszer működését. Kicsit fellengzősen Laposföld-imádóknak nevezi Newton követőit, akik mesterüket követve azt hirdették, hogy a Föld a sarkain laposabb, mint az egyenlítőn. (A köznyelvben a lapos Föld egészen mást jelent!) A korábban alkotó spekulatív Descartes szerint fordítva van: a Föld az egyenlítőn laposabb. Igazságot csak két nagy expedíció szolgáltatott Newtonnak. Hosszas kitérővel a szerzők eljutnak a jelentős francia fizikusnőhöz, Émilie de Chatelethez, aki a felvilágosodás egy főszereplőjével, mellesleges szeretőjével, Voltaire-rel együtt sikerrel népszerűsítette a newtoni tanokat. Találkozunk olasz nőkkel is, akik amatőrként a 18. századi tudomány élvonalába küzdik föl magukat. Például Laura Bassi Verattival, aki a bolognai egyetemen doktorált és lett a világ első női professzora.

Később megismerkedünk a 20. század legnagyobb matematikusnőjével, Emmi Noetherrel is, akit még 1920 körül is csak csellel tudott a göttingeni egyetemen alkalmazni Hilbert (12. fejezet. Forradalmak). Algebrai munkássága révén a matematikai fizikában is alapvető eredményeket ért el: szimmetriák alapján igazolta a fizika megmaradási tételeit.

A matematikus nők után folytassuk a nem európaiak matematikájával. Néhány témát sorolok föl távirati stílusban: ókori matematika (1. fejezet. A kezdet kezdetén.), kínai matematika (2. fejezet. Teknős és a császár), indiai matematika (5. fejezet. A nulla eredete(i)), arab matematika (6. fejezet: A Bölcsesség háza).

Nagyon szép ábrák mutatják be a különféle civilizációk számait. Érdekes, amit a negatív számok, mint adósság értelmezéséről írt. (Eddig azt hittem, hogy a negatív számokat Itáliában fedezték föl a 16. században.)

Nem maradhat el a 20. század elejének rejtélyes indiai zsenije sem: Rámánudzsan. Nem járt egyetemre, magasabb matematikai tudását egy képletgyűjteményből szerezte. Közönséges halandók számára érthetetlen módon megsejtett nagyon bonyolult matematikai összefüggéseket. Ezekből néhányat mutatóba elküldött Hardynak, aki nem értette, hogy juthat el valaki ezekhez. Littlewooddal összefogva meghívták Rámánudzsant Cambridge-be, és tapintatosan együttműködve számos sejtését szabatosan igazolták hármasban.

Ami nem tetszett

Túl laza. Híve vagyok a könnyedségnek, de számomra gyakran zavaró a nyelvi lazaság. (Feltételezem, hogy a gördülékenyen fordító Szegedi Péter stilárisan is híven adta vissza az angol szöveget.) Vegyük a tartalomjegyzéket! Alex nevű város? (Alexandria beceneve.) Kilenc fejezet, amely megváltoztatta a világot? (Félek, hogy az olvasók zöme nem találkozott a Tíz nap, amely megrengette a világot című könyvvel, amelyben John Reed amerikai újságíró leírta Leninék forradalmát.) Számháború? (Gyerekkoromban játszottam, ma már valószínűleg kiment a divatból.)

Kisebbségi matematika. Bevallom, hogy nem lelkesedem a „kisebbségi matematika történetének” ötletért, mert a domináns európai központú matematikatörténet előzetes ismerete nélkül nehéz elmondani a háttérbe szorítottak történetét.

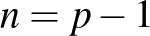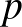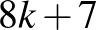A könyvben gyakran erőltetett az ugrás a közismert matematikából az ismeretlenbe. Például Sophie Germain francia matematikusnő eredményeit ismertetve (205. o.), a szerzők azt írják, hogy Gauss szerint a hősnő „Fermat-sejtés bizonyítása csak akkor működik, ha $n=p-1$ , ahol $p$ egy $8k+7$ alakú prímszám.” A Wikipédia szerint viszont Germain eleve ebben az alakban mondta ki a sejtést, és Gauss szerint a bizonyításban még további feltevés is rejlett. Közben még az is rejtve marad, hogy a szupersztár Euler 1740 körül bizonyította az első lépést: az 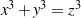$x^+y^3=z^3$ egyenletnek nincs pozitív egész megoldása.

Ugyancsak túlzónak találom a keralai matematikáról szóló részt (Egy iskola az indiai Keralában). Minden kalkulustankönyv látványosan tálalja (az 1670 körüli) Newtontól, Gregorytól és Leibniztől származó

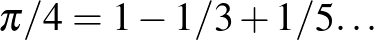
$\displaystyle \pi/4=1-1/3+1/5{\dots}$

végtelen sort, amely egyszerűen adódik, ha vesszük az 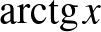$\operatorname{arctg} x$ hatványsor helyettesítési értékét az 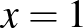$x=1$ helyen. Matematikus történészek rendre előhozzák, hogy Indiában már 200–300 évvel korábban tudták ezt az eredményt. Bevallom, nehezen hiszem el a történetet, és kétségeimet tovább erősíti, hogy korábban a még 1501-ben alkotó Nílakanthának tulajdonították az eredményt (Simonovits, 2009, 190. o.), de a recenzeált könyv 8. fejezetében már az 1340 körül alkotó Mádhavának. És engem külön zavar, hogy ez a bizonytalannak tűnő gondolatsor vezeti be a kalkulus történetét.

Meglepő, hogy a 15. fejezetben (A számháború) az úgynevezett nagy prímszámtétel is előkerül, amely az 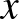$x$ -nél kisebb prímek számát, 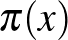$\pi(x)$ -et becsüli meg. Olyan bonyolult területről van szó, hogy 1965-ben én még azt sem tanultam a matematikusoknak tartott számelméleti kurzusban, hogy a legegyszerűbb aszimptotikus közelítés 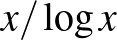$x/\log x$ (de la Vallée Poussin–Hadamard, 1895). Könyvünk ezen messze túllép: a Gauss sejtette, sokkal jobban közelítő 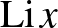$\operatorname{Li}x$ függvényt ismerteti. Sőt, a 276. oldalon például megadja, hogy az úgynevezett 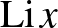$\operatorname{Li}x$ függvény 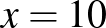$x=10$ millióig következetesen felülbecsli 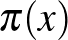$\pi(x)$ -et. Találkozunk két híres brit matematikussal, Hardyval és Littlewooddal, akik belátják, hogy nagyobb számokra az alulbecslés végtelen sokszor előfordul. E kitérőnek vélhetőleg egyetlen oka volt, hogy a fordulópont felfedezője, Skewes dél-afrikai (fehér férfi) volt! Ez tipikusan a gombhoz vart kabát esete.

Más didaktikai problémákat is megemlítek. A könyv kiemeli a sumérok 60-as számrendszerének azt az előnyét a 10-es számrendszerrel szemben, hogy a sok osztó miatt nem szembesül a végtelen tizedestörtek problémájával. Valóban, az 1/3 óra kerek 20 perc, ellentétben egy 100 percre osztott órával, ahol 33,333... perc lenne. De hallgat a 60-as számrendszer nagy hátrányáról: 60 darab számjegyet kell definiálniuk, szemben az indiai 10-zel.

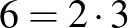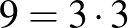A valóban fontos algoritmusoknál ismerteti két szám legnagyobb közös osztójának hatékony megkeresését (115–116. o.). A választott példa túl egyszerű: $6=2\cdot 3$ és $9=3\cdot 3$ legnagyobb közös osztója valóban 3, de ennél nagyobb számpárokon kellett volna érzékeltetni a problémát.

Dicsértem a könyvet hasznos ábráiért, de számos ábra használhatatlan. Például gyönyörű keleti miniatúrák fekete-fehér alapon. A fényképek jelentős része is elfogadhatatlan minőségű.

Végül egy apróság. Egy matematikatörténeti könyvben nem lenne szabad olyan durva becslést leírni, hogy „ez idő tájt mutatta ki Kopernikusz, hogy a bolygók a Nap, és nem a Föld körül keringenek, megdöntve ezzel Ptolemaiosz ezer évvel korábbi nézetét ...” (122. o.). 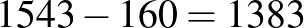$1543-160=1383$ !

Simonovits András
professor emeritus, BME Analízis és Operációkutatás Tanszék

Hivatkozás

: (Simonovits, 2009) Simonovits A. Válogatott fejezetek a matematika történetéből, TypoTeX Kiadó, 2009.
https://www.typotex.hu/book/1663/simonovits_andras_valogatott_fejezetek_a_matematika_tortenetebol

Információk