Molnár Zoltán Gábor (szerk.): Russelltől Gödelig. Esszék a matematika filozófiai problémáiról. Typotex, 2020.
„Könyvem kilátásai tehát kedvezőtlenek. Minden bizonnyal félretolják azok a matematikusok, akik olyan logikai kifejezések felbukkanásakor, mint »fogalom«, »reláció«, »ítélet«, ezt gondolják: metaphysica sunt, non leguntur! [metafizika következik, nem olvasandó], hasonlóképpen azok a filozófusok, akik ha megpillantanak egy formulát, így kiáltanak fel: mathematica sunt, non leguntur!; és nagyon kevesen lehetnek, akik nem ilyenek. ” (Frege, G. (2000)., p. 154.)
Bár e gyakran idézett sorok 128 évvel ezelőtt jelentek meg a modern matematikafilozófia egyik megalapítójának tekinthető Gottlob Frege Az aritmetika alaptörvényei című művének bevezetésében, a klasszikus matematikafilozófiai szövegek szélesebb közönséghez való eljuttatása napjainkban is komoly kihívást jelentő feladat, jelentős részben a Frege által említettekhez hasonló okokból. A matematikában járatosabbak számára gyakran idegenek a matematikafilozófia kérdésfeltevései, fogalomhasználata és érvelési stílusa, míg a filozófiában otthonosabban mozgók közül sokakat elriasztanak a rendszeresen előforduló technikai jellegű, komolyabb matematikai felkészültséget igénylő részletek.
A Russelltől Gödelig írásainak célközönsége főként az első csoport: a kötet kilenc esszéje a Műegyetem „A matematika filozófiai alapjai és alkalmazásai” című olvasószemináriumán feldolgozott, nagyrészt magyarul is elérhető szövegeket próbálja közelebb hozni a matematikai érdeklődésű olvasókhoz a tárgyalt problémák, fogalmak elemzésével, tágabb kontextusba helyezésével és néhány kiemelkedő fontosságú gondolatmenet részletes rekonstrukciójával.
Az első két írás, amelyeket a kötetet szerkesztő Molnár Zoltán Gábor jegyez, Frege „Jelentés és jelölet” és Bertrand Russell „A denotálásról” című cikkét elemzi. Mindkét szöveg a korai analitikus filozófia klasszikusa, de egyikük tárgya sem kifejezetten matematikai: a „Jelentés és jelölet” Frege legnagyobb hatású nyelvfilozófiai írása, amely az általa javasolt kétaspektusú jelentéselmélet alapjait fejti ki, Russell cikke pedig Frege szemantikáját kritizálva egy ontológiailag és ismeretelméletileg jóval takarékosabb alternatíva mellett érvel. A kötetben való tárgyalásuk mégsem mondható indokolatlannak. Egyrészt jó bevezetést nyújtanak az analitikus filozófiai tradícióba, amelynek szemlélete meghatározó a kortárs matematikafilozófiában, és amelyhez a kötetben tárgyalt összes írás közel áll. Másrészt – és ez talán a fontosabb ok – számos ponton kapcsolódnak későbbi, a kötet további írásaiban is fontos szerepet játszó matematikafilozófiai és modellelméleti fejleményekhez. Molnár Frege-esszéje hasznos áttekintést nyújt néhány a „Jelentés és jelölet”-tel nagyjából egyidős, utóbb szintén komoly karriert befutott szemantikai elméletről, és mesterien mutatja meg, hogy bizonyos Frege által tárgyalt jelentéselméleti problémák hogyan jelennek meg, és miképpen kezelhetők a modern – Tarski utáni – modellelmélet keretei között. A második esszé szintén a Tarski által megalapozott szemantikai perspektívából veszi szemügyre Russellnek az általa denotálónak nevezett kifejezések, többek között a határozott leírások jelentésére vonatkozó elméletét, és részletesen rekonstruálja Russell híres-hírhedt, Frege szemantikájának inkoherenciáját igazolni hivatott „Gray elégiája” érvét.
A következő hat írás már egyértelműen matematikafilozófiai tárgyú, szintén klasszikusnak tekinthető szövegeket, illetve problémákat tárgyal, amelyek tartalmilag szorosan összetartoznak. A kötet magját alkotó esszécsoport tematikus középpontjában Kurt Gödel nevezetes, 1951-es Gibbs-előadása áll. Molnár Zoltán Gábor és Lévai Emese Sarolta esszéi kifejezetten Gödel előadását elemzik, és a másik négy írás is az előadás alaptémájához kapcsolódik, nevezetesen ahhoz, hogy Gödel nemteljességi tételeivel kezdődően számos olyan matematikai eredmény született, melyek filozófiailag is kiemelkedő jelentőségűek, többek között mivel a „matematika befejezhetetlenségét vagy kimeríthetetlenségét” látszanak igazolni.
Molnár az első esszében rendkívül hasznosan bontja ki Gödel olykor meglehetősen technikai halmaz- és a számelméleti bevezető megjegyzeséinek matematikai hátterét, és jó szemmel mutat rá, hogy a gondolatmenet bizonyos pontjain összecsúszik az axiomatizálás és az algoritmikus generálás egymást nem teljesen fedő fogalma. Az írás második fele Gödelnek az ismertetett matematikai eredményekre épített matematikafilozófiai alaptézisét, a »diszjunktív tézist«, és ebből kiinduló, matematikai platonizmus mellett szóló érveit tárgyalja. Gödel tézise szerint
„[a] matematika vagy lényege szerint befejezhetetlen, abban az értelemben, hogy evidens axiómái soha nem foglalhatók össze egy véges szabályban, vagyis az emberi elme (még a tiszta matematika területén is) végtelenül meghaladja bármely véges gép teljesítőképességét – vagy pedig léteznek (a fent leírt típusba tartozó) abszolút megoldhatatlan diofantikus problémák. ” (Gödel, K. (2003)., p. 69.)
Molnár részletesen elemzi a tézis mögött álló, a második nemteljességi tételre építő érvrendszert és buktatóit; különösen figyelemreméltóak a konzisztencia véges jellegű, de a tételnek mégsem ellentmondó igazolási lehetőségeire vonatkozó megjegyzései. Az írást az előadás platonista konklúziójának értékelése zárja: a szerző meggyőzően érvel amellett, hogy Gödel gondolatmenete valójában csak azt igazolja, hogy a matematikai realizmus kompatibilis a diszjunktív tézissel.
A kötet másik, szintén a Gibbs-előadást tárgyaló esszéjében Lévai Emese Sarolta rendhagyó, narratológiai-dramaturgiai nézőpontból vizsgálja a szöveget, és azt mutatja meg, hogy Gödel narratívája nem teljesen egységes: több, különböző világlátással és filozófiai nézőponttal rendelkező elbeszélő különböztethető meg benne, akiknek a párbeszéde minden bizonnyal Gödel saját belső dialógusát, önmagával folytatott vitáit képezi le.
Mint már említettük, a többi négy matematikafilozófiai tárgyú írás mindegyike köthető Gödel előadásának bizonyos témáihoz. Sorrendben az első Márton Gábor az „»Aritmechanikus« gépek tündöklése és alkonya” című nagylélegzetű esszéje, amely a Gödel-számozás fogalmától kezdve Kleene általános rekurzív függvényekre vonatkozó tételein keresztül a Turing-gépek megállási problémájának algoritmikus eldönthetetetlenségéig kivételes részletességgel és precizitással ismerteti azokat az 1930-as években született matematikai eszközöket és eredményeket, amelyek együttesen legalábbis felvethetővé teszik abszolút megoldhatatlan matematikai problémák létezésének a lehetőségét. Nagy erénye a szövegnek, hogy nem elégszik meg a hasonló alapgondolatokra épülő bizonyítások puszta egymás mellé helyezésével, hanem külön szakaszt szentel a közös elemek (ilyen pl. Cantor átlós módszerének alkalmazása) elemzésének.
Az effektív, mechanikus eszközökkel való kiszámíthatóság informális fogalma és a Turing-kiszámíthatóság precízen definiált matematikai fogalma közötti kapcsolatot természetesen a széles körben elfogadott Church–Turing-tézis teremti meg, amely szerint minden effektíven kiszámítható függvény Turing-kiszámítható. Ha a tézis igaz, akkor – mint erre már Márton esszéjének bevezetése is kitér – a Kleene és Turing által konstruált nem Turing-kiszámítható függvények semmilyen effektív eszközzel sem számíthatók ki, holott matematikailag jól definiált, totális, természetes számokat vagy természetes számok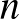 
-eseit természetes számokra képező függvényekről van szó. Ráadásul a helyzet furcsaságát fokozzák a konstrukciók bizonyos részletei. Vegyük például a Turing-gépek megállási problémájának megfelelő, számpárokon értelmezett függvényt, amelynek értéke egy 
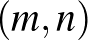számpárra 1, ha az 
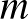indexű Turing-gép megáll az 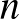inputra, és 0 egyébként. Erről a függvényről bebizonyították, hogy nem Turing-kiszámítható, tehát a Church–Turing-tézis szerint effektíven sem kiszámítható. De mit jelent ez a konkrét függvényértékek kiszámítására nézve? Úgy tűnhet, hogy azokra a párokra, amelyekre 1 a függvény értéke, rendelkezünk effektív kiszámítási eljárással, hiszen elegendő „futtatni” a kérdéses Turing-gépet az adott inputon, és kivárni, hogy megálljon. Azokra a párokra, amelyekre 0 a függvény értéke, viszont kereshetünk olyan bizonyítást, amely igazolja, hogy az adott gép nem áll meg az adott inputra. Könnyen támadhat az a benyomásunk, hogy ha e két stratégia kombinációja a Church–Turing-tézissel összhangban nem effektív kiszámítási eljárás a teljes függvényre nézve, akkor léteznie kell legalább egy olyan számpárnak, amelyre a függvény értéke 0, tehát a megfelelő gép az adott inputra nem áll meg, de ez a tény semmiféle effektív módon megtalálható bizonyítással sem igazolható (nevezhetjük akár „abszolút bizonyíthatatlan problémának” is) annak ellenére, hogy a most előadott gondolatmenetünkből következni látszik.
A Church–Turing-tézissel kapcsolatos imént vázolt furcsaság annyiban nem puszta kuriózum, hogy hasonló megfontolásokra épül Kalmár László két nevezetes, a tézis plauzibilitása ellen érvelő cikke is, amelyeket a kötetben Molnár Zoltán Gábor egy esszéje elemez. Molnár rekonstruálja Kalmár reductio ad absurdumot alkalmazó érvének lépéseit, és tüzetesen megvizsgálja azt az érvben központi szerepet játszó eljárást is, amelyről Kalmár azt állítja, hogy annak ellenére effektív, véges eljárás, hogy az általa kiszámított függvény nem Turing-kiszámítható. Az írás gondosan rámutat Kalmár érvelésének gyenge pontjaira, és rendkívül fontos észrevétele, hogy a kizárt harmadik elve a Church–Turing-tézissel egyenrangú premisszája a reductiónak, ezért az ellentmondás úgy is feloldható, hogy az előbbit vetjük el, elfogadva, hogy a metamatematika – a klasszikus logikájú matematika metatudománya – nem klasszikus, hanem valamilyen konstruktív, például intucionista logikát követ.
A konstrukív metamatematika és az intuicionista logika témája egyúttal átvezet minket a kötet két hátralevő, szintén a szerkesztőtől származó matematikafilozófiai írásához, amelyek a két klasszikus konstruktivista irányzathoz, a finitizmushoz és az intuicionizmushoz kapcsolódnak. A konstruktivista perspektíva folyamatosan jelen van a Gibbs-előadás szövegében is: Gödel részletekbe menően érvel amellett, hogy a diszjunktív tézis egy alakja érvényes az intuicionisták és finitisták felfogása szerint is, és szövegében felbukkan egy olyan, általa „szubjektívnek” nevezett alternatív matematikafelfogás is, amely a matematikai igazságot a bizonyíthatósággal azonosítja, ami természetesen az intuicionizmus egy befolyásos interpretációjához köthető nézet.
A finitizmussal foglalkozó esszé William W. Taitnek a finit matematikáról szóló alapvető tanulmányát tárgyalja, amelynek vitatott, de nagyhatású tézise szerint a finit matematika azonos a primitív rekurzív aritmetikával. Molnár szövege ügyesen ötvözi a történeti, Hilbert programjához köthető finitizmus bizonyos elemeinek bemutatását Tait gondolatmenetének ismertetésével, szembesítve a Tait által javasolt finitista szám- függvény- és bizonyításfogalmat Hilbert nézeteivel.
A másik írásban elemzett tanulmány témája kevésbé közvetlenül kapcsolódik a konstruktivizmushoz, de a kapcsolat kétségkívül fennáll: a szerző Michael Dummett, aki a jelentés használatelméletéből kiindulva számos művében érvelt amellett, hogy a matematika logikájának az intuicionista logikát kell tekinteni, és „A Gödel-tétel filozófiai jelentősége” című cikkében azt vizsgálja, hogy az első nemteljességi tétel ellentmond-e ennek a szemantikai megközelítésnek. Molnár ismerteti a modellelméleti megfontolásokra támaszkodó ellenérvet, amelyet Dummett tárgyal, és jól választott példákon keresztül világítja meg a benne kulcsszerepet játszó megkülönböztetést egy axiómarendszer szenderd, illetve nem-sztenderd modelljei között. Az esszé Dummett következtetéseivel összhangban álló konklúziója szerint a nemteljességi tétel éppen hogy nem a használatelméletnek, hanem a modellelméleti ellenérv alapjául szolgáló, a természetes számokra, illetve a halmazelméletre vonatkozó realizmusnak mond ellent.
A utolsó tanulmány, a kötetnek mintegy keretes szerkezetet kölcsönözve, az első két esszéhez hasonlóan nem matematikafilozófiai, hanem referenciaelméleti és ismeretelméleti tárgyú szöveget tárgyal: Hilary Putnam „Agyak a tartályban” című írását dolgozza fel, amely szemantikai premisszákra építve érvel a címben szereplő „agyak vagyunk a tartályban” szkeptikus hipotézis inkoherenciája mellett. Varga Bálint esszéje vázolja a Putnam kiindulópontjául szolgáló externalista, kauzális referenciaelméletet, bemutatja elmefilozófiai vonatkozásait, és kitér Putnam érvének utóéletére is, ismertetve néhány befolyásos rekonstrukciót, illetve kritikát.
Az egyes esszék rövid tartalmi áttekintése után mit mondhatunk a kötet egészéről? A recenzió elején említett cél, vagyis alapvető matematikafilozófiai szövegek szélesebb közönséghez való eljuttatása szempontjából a Russelltől Gödelig kifejezetten ígéretes. A feldolgozott írások nagy többsége olyan klasszikus, amely alkalmas arra, hogy a kötetben található esszékkel együtt bevezetőként szolgáljon egy-egy fontos matematikafilozófiai témába, a Gibbs-előadás középpontba állítása pedig egyenesen telitalálat, mivel Gödel önmagukban is sokak fantáziáját megmozgató matematikai tételekre épít izgalmas filozófiai következtetéseket, és a szöveg – jelentős részben a Lévai Emese Sarolta esszéjében kimutatott sokszólamúsága okán – nagyszámú kapcsolódási pontot kínál a többi tanulmányhoz. Az elemzett írások szerencsés kiválasztásán felül a szerkesztő és a szerzők nagy hangsúlyt fektettek arra is, hogy esszéik filozófiai iskolázottság nélkül is érthetőek legyenek, és matematikai, illetve logikai téren sem várnak el több előképzettséget az olvasótól, mint amivel egy egyetemi hallgató egy-két bevezető kurzus elvégzése után már biztosan rendelkezik.
Ha a kötet kapcsán hiányosságról beszélhetünk, akkor az leginkább néhány olyan téma, illetve konkrét cikk tárgyalásának hiánya, amelyek egyértelműen beleillettek volna a kötet koncepciójába. Különösen Paul Benacerraf két klasszikus írása, a strukturalizmus programadó művének számító „Amik a számok nem lehetnek” (2003), valamint a platonizmus és a tudás kauzális elmélete közt fennálló ellentmondásra rámutató „Matematikai igazság” (1973) említhető ezek között. Ha nem is szükségképpen önálló elemző esszé formájában, de szintén érdemes lett volna kitérni Daniel Isaacson (1987) figyelemreméltó tézisére is, amely szerint a Peano-aritmetika abban az értelemben teljes, hogy a benne eldönthetetlen állítások igazsága csak nem tisztán aritmetikai, „magasabb rendű” fogalmakra is hivatkozó megfontolások alapján látható be. Reméljük, hogy a folytatásban – mert a Russelltől Gödelig mindenképpen folytatásra érdemes, akár egy újabb hasonló kötet, akár egy második kiadás formájában – már ezek az írások is szerephez jutnak majd.
Irodalomjegyzék
Benacerraf, P. (1973). Mathematical truth. Journal of Philosophy, 70(19), 661–679.
Benacerraf, P. (2003). Amik a számok nem lehetnek. In Csaba, F. (Ed.), A matematika filozófiája a 21. század küszöbén (pp. 165–196). Budapest: Osiris Kiadó.
Frege, G. (2000). Az aritmetika alaptörvényei. I. kötet (részletek). In Máté, A. (Ed.), Logikai vizsgálódások (pp. 148–178). Budapest: Osiris Kiadó.
Gödel, K. (2003). Néhány tétel a matematika megalapozásáról és ezek következményei. In Csaba, F. (Ed.), A matematika filozófiája a 21. század küszöbén (pp. 61–88). Budapest: Osiris Kiadó.
Isaacson, D. (1987). Arithmetical truth and hidden higher-order concepts. In Logic Colloquium ’85 (Vol. 122, pp. 147–169). Elsevier.
Simonyi András, ELTE Informatikai Kar, Neurális Információfeldolgozási Csoport