Egyszerű kérdések, bonyolult válaszok – III. A Lebesgue-felbontás

1. Bevezető

Mielőtt rátérünk a cikk tartalmi részére – nevezetesen a mértékelmélet egyik alaptételének egy olyan bizonyítására, amely a lineáris altérre vett zárlat tulajdonságaival operál – röviden felidézünk néhány alapfogalmat.

Egy $X$ halmaz részhalmazaiból álló $\mathcal{A}\neq\emptyset$ halmazrendszer $\sigma$ -algebra, ha zárt a komplementer és a megszámlálható unió képzésére. Egy $A\in\mathcal{A}$ halmaz karakterisztikus függvényét $\mathds{1}_A$ -val jelöljük, azaz

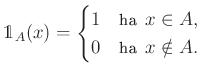
$\displaystyle \mathds{1}_A(x)=\begin{cases}1 & \text{ha } x \in A,\\ 0 & \text{ha } x \notin A. \end{cases}$

Egy $\mu\colon \mathcal{A}\to[0,\infty)$ halmazfüggvényt nemnegatív véges mértéknek nevezünk, ha az alábbi két feltételt teljesíti:

(i) $0\leq\mu(X)<+\infty$ ,

(ii) ha $(A_n)_{n\in\mathbb{N}}$ egy olyan $\mathcal{A}$ -ban haladó halmazsorozat, hogy tetszőleges $j\neq k$ esetén $A_j\cap A_k=\emptyset$ , akkor

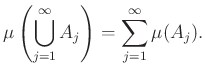
$\displaystyle \mu\left(\bigcup_{j=1}^{\infty}A_j\right)=\sum_{j=1}^{\infty}\mu(A_j).$

Az $\mathcal{A}$ $\sigma$ -algebrához természetes módon asszociálódik a valós $\mathcal{A}$ -lépcsős függvények $\mathcal{E}$ -vel jelölt vektortere. Emlékeztetünk, hogy egy $f\colon X\to\mathbb{R}$ függvényt $\mathcal{A}$ -lépcsős függvénynek nevezünk, ha $\mathcal{A}$ -beli halmazok karaktersztikus függvényeinek véges lineáris kombinációja. Azaz ha van olyan $A_1,\dots,A_n$ véges $\mathcal{A}$ -beli halmazrendszer és $c_1,\dots,c_n$ valós szám $n$ -es, amelyre

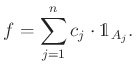
$\displaystyle f=\sum_{j=1}^n c_j\cdot\mathds{1}_{A_j}.$

Hasonlóan természetes módon adódik egy egyszerű integrálfogalom az $\mathcal{A}$ -lépcsős függvények vektorterén. A fenti felírású $f$ függvény $\mu$ szerinti integrálján az

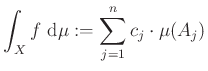
$\displaystyle \int_X f~\mathrm{d}\mu:=\sum_{j=1}^n c_j\cdot\mu(A_j)$

számot értjük. Az így kapott integrál jóldefiniált, azaz az integrál értéke nem függ $f$ előállításától. Megjegyezzük, hogy két $\mathcal{A}$ -lépcsős függvény szorzata is $\mathcal{A}$ -lépcsős függvény, így ha $f,g\in\mathcal{E}$ , akkor $\int_X fg~\mathrm{d}\mu$ továbbra is egy véges összeget jelöl, tehát a fentinél bonyolultabb integrálfogalomra nem lesz szükségünk. Végül bevezetünk egy jelölést: az $f$ $\mathcal{A}$ -lépcsős függvény tartóját, azaz az $\{x\in X\mid f(x)\neq0\}$ halmazt röviden $[f\neq0]$ -val jelöljük.

2. Abszolút folytonosság és altérre vonatkozó zárlat

Mostantól $\mu$ és $\nu$ mindig két nemnegatív véges mértéket jelöl. Azt mondjuk, hogy $\mu$ abszolút folytonos a $\nu$ -re nézve (jelekkel: $\mu\ll\nu)$ , ha

$\displaystyle \forall A\in\mathcal{A}\colon \nu(A)=0\Longrightarrow\mu(A)=0.$

Megjegyezzük, hogy ez a folytonosság fogalom azért képes ilyen egyszerű, ránézésre meglehetősen algebrai alakot ölteni, mert a $\sigma$ -additivitás rásegít a

$\displaystyle \forall\varepsilon>0\quad\exists\delta>0\quad\forall A\in\mathcal{A}\colon\nu(A)<\delta \Longrightarrow \mu(A)<\varepsilon$

definícióra. Az abszolút folytonosság fogalmának jelentőségére a Radon-Nikodym tétel világít rá: a $\mu$ mértéknek pontosan akkor létezik sűrűségfüggvénye a $\nu$ -re vonatkozóan, ha $\mu\ll\nu$ .

De mi köze van a mértékek abszolút folytonosságának a mátrixok alterekre vonatkozó zárlatához? Pozitív szemidefinit (és így önadjungált) mátrixok esetén a képtér és a magtér, azaz a

$\displaystyle \operatorname{ran}A=\{Ax\mid x\in H\}$ és $\displaystyle \quad\ker A=\{x\in H\mid Ax=0\}$

alterek egymásra merőlegesek, és így a $\operatorname{ran}A\subseteq\operatorname{ran}B$ tartalmazás ekvivalens azzal, hogy $\ker B\subseteq\ker A$ . Ez utóbbit másképp felírva azt kapjuk, hogy

$\displaystyle \forall x\in H\colon Bx=0 \Longrightarrow Ax=0,$

ami pedig az abszolút folytonosság fogalmára legalábbis formailag nagyon hasonlít. Két tetszőlegesen választott $A$ és $B$ pozitív szemidefinit mátrixra a $\operatorname{ran}A\subseteq\operatorname{ran}B$ tartalmazás természetesen nem teljesül. De az altérre vonatkozó zárlat fogalma (az $\mathcal{S}=\operatorname{ran}B$ választással) épp azt garantálja, hogy az

$\displaystyle M(A,\operatorname{ran}B):=\big\{C\in\mathbf{B}_+(H)\mid C\leq A$ és $\displaystyle \operatorname{ran}C\subseteq\operatorname{ran}B\big\}$

halmaznak van legnagyobb eleme, nevezetesen $A_{/\operatorname{ran}B}$ . Más szóval, $A$ -nak van egy olyan extremális tulajdonságokkal bíró része, amelynek képtere része $B$ képterének. Könnyű megmutatni, hogy a maradék, azaz az $A-A_{/\operatorname{ran}B}$ mátrix képtere a $B$ mátrix képterétől már amennyire csak lehet, diszjunkt:

$\displaystyle \operatorname{ran}(A-A_{/\operatorname{ran}B})\cap\operatorname{ran}B=\{0\}.$

Ez a képterekre vonatkozó állítás (a Douglas majorizációs és faktorizációs tétel értelmében) ekvivalens azzal, hogy ha egy $C\in\mathbf{B}_+(H)$ mátrixra $C\leq A$ és $C\leq B$ egyidejűleg teljesül, akkor $C$ a nulla mátrix.

Ezt a sémát akarjuk tehát követni nemnegatív véges mértékek esetén is. Igaz-e, hogy ha $\mu$ maga nem is abszolút folytonos $\nu$ -re nézve, akkor is le lehet választani belőle egy lehető legnagyobb $\nu$ -abszolút folytonos részt? Milyen értelemben lesz a maradék a $\nu$ -től diszjunkt?

Először is, ahhoz hogy beszélhessünk legnagyobb elemről, be kell vezetnünk egy részbenrendezést a nemnegatív mértékek halmazán:

$\displaystyle \mu_1\leq\mu_2\Leftrightarrow\forall A\in\mathcal{A}\colon \mu_1(A)\leq\mu_2(A).$

Azt mondjuk, hogy $\mu$ és $\nu$ szingulárisak (jelekkel: $\mu\perp\nu$ ), ha van olyan $P\in\mathcal{A}$ halmaz, amelyre $\mu(P)=\nu(X\setminus P)=0$ . Ez a tulajdonság ekvivalens azzal, hogy ha $\eta$ egy olyan nemnegatív véges mérték, amelyre $\eta\leq\mu$ és $\eta\leq\nu$ egyszerre teljesül, akkor $\eta$ szükségképpen a nulla mérték. Világos tehát az analógia, az a kérdés, hogy hogyan profitáljunk belőle. Természetes ötlet, hogy valahogy fogalmazzuk át a mértékek nyelvére a

$\displaystyle \forall x\in H\colon(A_{/\operatorname{ran}B}x,x)=\inf\limits_{y\in\ker B}(A(x-y),x-y)$

formulát. Az első kérdés, hogy mivel helyettesítsük a skalárszorzatot? Ha az $A$ mátrixot $\mu$ -re, az $x\in H$ vektort $f\in\mathcal{E}$ -re akarjuk fordítani, akkor az $(Ax,x)$ kifejezés átírására az $\int_X \vert f\vert^2~\mathrm{d}\mu$ a kézenfekvő választás. Ha a $B$ mátrixot a $\nu$ -re akarjuk lefordítani, akkor a $\ker B=\{x\in H\mid Bx=0\}$ lineárisaltér megfelelője $\mathcal{E}$ -ben

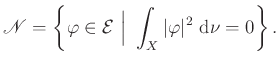
$\displaystyle \mathscr{N}=\left\{\varphi\in\mathcal{E}\ \Big\vert\ \int_X\vert\varphi\vert^2~\mathrm{d}\nu=0\right\}.$

Ezek után már könnyű kiokoskodni, hogy az $A_{/\operatorname{ran}B}$ mátrix megfelelője a

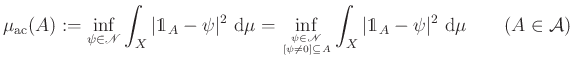
$\displaystyle \mu_{\mathrm{ac}}(A):=\inf\limits_{\psi\in\mathscr{N}}\int_X\vert... ... A}} \int_X\vert\mathds{1}_A-\psi\vert^2~\mathrm{d}\mu\qquad(A\in\mathcal{A})$

halmazfüggvény. Mint azt a következő fejezetben látni fogjuk, azzal hogy a fordítás kész, lényegében minden munkát elvégeztünk. Mielőtt rátérnénk a bizonyításra, teszünk még egy megjegyzést. Ahogy arra az abszolút folytonosság definíciójánál utaltunk, az egyszerűség hátterében ott munkálkodik a $\sigma$ -additivitás. Az olvasóban felébredhet a gyanú, hogy valami a mátrixokra vonatkozó fogalom hátterében is munkálkodik, hiszen ott tényleg csak egy lineáris algebrai definícióról van szó, topológiának semmi nyoma. Való igaz, az hogy ez a fogalom ilyen egyszerű alakot öltött, az annak köszönhető, hogy $H$ véges dimenziós volt, és így a $\operatorname{ran}B$ képtér automatikusan zárt. Ha $H$ nem véges dimenziós, akkor a $B$ -ről külön fel kell tenni, hogy zárt képterű.

3. A Lebesgue-felbontás

Tétel: Legyen $\mu$ és $\nu$ két tetszőleges nemnegatív véges mérték az $\mathcal{A}$ $\sigma$ -algebrán. Ekkor $\mu$ -nek létezik egy és csak egy olyan $\mu=\mu_1+\mu_2$ felbontása, ahol $\mu_1\ll\nu$ és $\mu_2\perp\nu$ .

Bizonyítás: Mivel egy nemnegatív függvény integrálja nemnegatív, $\mathds{1}_{\emptyset}\in\mathcal{N}$ , és $\nu(A)=0$ esetén $\mathds{1}_A\in\mathcal{N}$ , ezért a $\mu_{\mathrm{ac}}$ definícióra ránézve világos, hogy $\mu_{\mathrm{ac}}$ nemnegatív, $\mu_{\mathrm{ac}}\leq\mu$ , és hogy $\mu_{\mathrm{ac}}(A)=0$ . Azt is könnyű ellenőrizni, hogy $\mu_{\mathrm{ac}}$ végesen additív, mert ha $A_1$ és $A_2$ diszjunkt $\mathcal{A}$ -beli halmazok, akkor

$\displaystyle \Big\{\psi\in\mathscr{N}~\Big\vert~[\psi\neq0]\subseteq A_1\cup A... ...psi_1+\psi_2\in\mathscr{N}~\Big\vert~[\psi_i\neq0]\subseteq A_i,~i=1,2\Big\}.$

Ebből viszont már következik $\mu_{\mathrm{ac}}$ $\sigma$ -additivitása, ugyanis

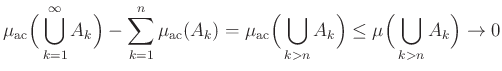
$\displaystyle \mu_{\mathrm{ac}}\Big(\bigcup\limits_{k=1}^{\infty}A_k\Big)-\sum\... ...\Big(\bigcup\limits_{k>n}A_k\Big)\leq\mu\Big(\bigcup\limits_{k>n}A_k\Big)\to0$

teljesül minden olyan halmazsorozatra, amelynek tagjai páronként diszjuntak. Már csak azt kell megmutatnunk, hogy a $\mu_{\mathrm{s}}:=\mu-\mu_{\mathrm{ac}}$ és $\nu$ mértékek szingulárisak, és hogy a felbontás egyértelmű. Mindkét állítás könnyen következik majd abból, hogy $\mu_{\mathrm{ac}}$ a legnagyobb elem azon $\vartheta$ nemnegatív véges mértékek között, amelyekre $\vartheta\leq\mu$ és $\vartheta\ll\nu$ egyszerre teljesül. Ahhoz hogy ezt belássuk, válasszunk egy $\psi\in\mathscr{N}$ függvényt, és vegyük észre, hogy

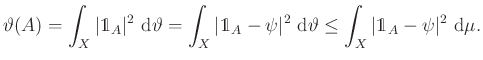
$\displaystyle \vartheta(A)=\int_X\vert\mathds{1}_A\vert^2~\mathrm{d}\vartheta=\... ...t^2~\mathrm{d}\vartheta\leq\int_X\vert\mathds{1}_A-\psi\vert^2~\mathrm{d}\mu.$

Az $\mathscr{N}$ elemeire infimumot véve azt kapjuk, hogy $\vartheta\leq\mu_{\mathrm{ac}}$ .

Ezek után legyen $\eta$ egy olyan nemnegatív véges mérték, amelyre $\eta\leq\nu$ és $\eta\leq\mu_{\mathrm{s}}$ . Ekkor $\mu_{\mathrm{ac}}+\eta\leq\mu$ és $\mu_{\mathrm{ac}}+\eta\ll\nu$ , következésképp $\eta=0$ , ami épp azt jelenti, hogy $\nu\perp\mu_{\mathrm{s}}$ .

Ha $\mu=\mu_1+\mu_2$ , a $\mu$ -nek egy olyan felbontása, amelyre $\mu_1\ll\nu$ és $\mu_2\perp\nu$ teljesül, akkor $\mu_{\mathrm{ac}}-\mu_1$ egy olyan nemnegatív véges mérték, amely egyszerre abszolút folytonos és szinguláris $\nu$ -re nézve. Ebből pedig az következik, hogy $\mu_1=\mu_{\mathrm{ac}}$ , és így $\mu_2=\mu_{\mathrm{s}}$ . Ezzel a tételt bebizonyítottuk.