A Héttusa 6. fordulójának feladatmegoldásai szokás szerint megjelentek az Érintő Facebook-oldalán. Kiegészítettük a megoldásokat a beküldők gondolataival, ötleteivel, hiszen egy-egy problémához mindenki másképp áll hozzá.
36. Feltehetünk-e 12 bábut egy 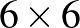 -os sakktáblára úgy, hogy mindegyik sorban, mindegyik oszlopban és a két átlóban is 2-2 bábu legyen? (Egy mezőre legfeljebb egy bábut tehetünk.)
-os sakktáblára úgy, hogy mindegyik sorban, mindegyik oszlopban és a két átlóban is 2-2 bábu legyen? (Egy mezőre legfeljebb egy bábut tehetünk.)
A válasz: Igen, lehet.
Megoldás. A beérkezett megoldásokból néhány jó kitöltés:
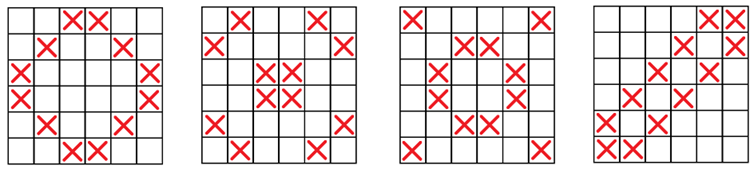
S. Ákos teljes indukcióval igazolja, hogy egy 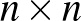 -es sakktáblán elhelyezhetünk
-es sakktáblán elhelyezhetünk 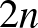 bábut úgy, hogy mindegyik sorban, mindegyik oszlopban és a két átlóban is 2-2 bábu legyen, ha
bábut úgy, hogy mindegyik sorban, mindegyik oszlopban és a két átlóban is 2-2 bábu legyen, ha 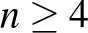 . Itt az indukciós lépésben
. Itt az indukciós lépésben 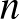 -ről
-ről  -re lépünk.
-re lépünk.
Ugyanezt Makay Géza is igazolja, eljárást ad a konstrukcióra páros, illetve páratlan 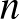 -ek esetén.
-ek esetén.
Az általános kérdést átfogóan elemzi Dombi Péter.
Udvari Tibor bizonyítja, hogy a 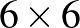 -os táblán elhelyezhetünk
-os táblán elhelyezhetünk 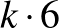 darab bábut úgy, hogy mindegyik sorban, mindegyik oszlopban és a két átlójában a bábuk száma
darab bábut úgy, hogy mindegyik sorban, mindegyik oszlopban és a két átlójában a bábuk száma 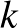 darab legyen, ahol
darab legyen, ahol 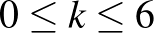 .
.
37. Egy 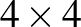 -es táblázatba 16 különböző természetes számot írtunk úgy, hogy a táblázat mindegyik sorában és mindegyik oszlopában ugyanannyi a számok szorzata. Lehetséges-e, hogy mindegyik beírt szám kisebb 100-nál?
-es táblázatba 16 különböző természetes számot írtunk úgy, hogy a táblázat mindegyik sorában és mindegyik oszlopában ugyanannyi a számok szorzata. Lehetséges-e, hogy mindegyik beírt szám kisebb 100-nál?
A válasz: Igen, lehetséges.
Megoldás. Készítünk négyféle színből 4-4 egybevágó négyzetlapot, és ezekre írjuk rá az 1, 2, 3, 4 számokat. Így mindegyik szám 4-szer szerepel, és mindegyik szám 4-féle színben látható. A számkártyák elrendezhetők úgy egy 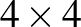 -es táblázatban, hogy mindegyik sorban és mindegyik oszlopban szerepel mind a négy szín, és mind a négy szám.
-es táblázatban, hogy mindegyik sorban és mindegyik oszlopban szerepel mind a négy szín, és mind a négy szám.
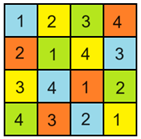
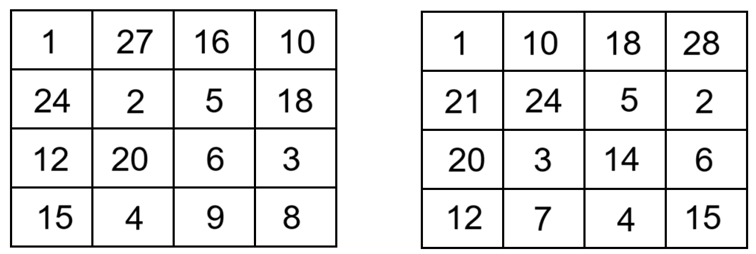
Használjuk ezt a táblázatot. A számok mintázata szerint töltöttük ki az első táblázatot az 1, 2, 3, 5 számokkal, és a színek mintázata szerint rendeztük el az 1, 7, 11, 13 számokat a második táblázatban.
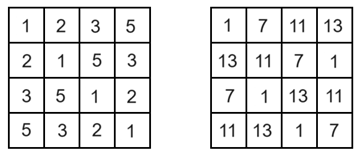
Ebből a két táblázatból adódik egy új táblázat úgy, hogy az azonos pozíciót elfoglaló számokat összeszorozzuk:
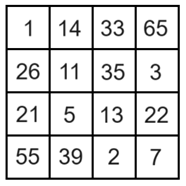
Itt bármelyik sorban, ill. bármelyik oszlopban a négy szám szorzata megegyezik az előző két táblázat elkészítéséhez használt nyolc szám (1, 2, 3, 5 és 1, 7, 11, 13) szorzatával. A táblázatban lévő számok szükségszerűen különbözőek, mivel ez a nyolc szám páronként relatív prím. Teljesül az az elvárás is, hogy a számok 100-nál kisebbek.
Izsák Beatrix próbálgatással talált jobb táblázatot, ahol a táblázatban a legnagyobb szám 27, és a szorzat 4320. Érkeztek olyan táblázatok is, ahol a legnagyobb szám 28, és a szorzat 5040.
Lássuk be, hogy a táblázatban lévő legnagyobb szám nem lehet kisebb 27-nél.
Tegyük fel, hogy a legnagyobb szám legfeljebb 26. Ekkor a táblázatba beírt 16 különböző szám között nem lehet ott például a 7, 14 és a 21. Hiszen ha valamelyiket beírjuk, akkor annak a sorában a számok szorzata osztható 7-tel. Minden sorban ugyanaz a szorzat, ezért mind a négy sorban lennie kell 7-tel osztható számnak.
Így gondolkodva a 16 kiválaszott szám között nem lehet ott ez a 10 szám: 7, 14, 21, 11, 22, 13, 26, 17, 19, 23.
Ezért a megmaradó 16 szám mindegyikét be kell írni a táblázatba. Nézzük az 5-tel osztható számokat: 5, 10, 15, 20 és 25. Mindegyik sorban 5-tel osztható a számok szorzata. Lesz olyan szorzat is, amely osztható 25-tel, ezért mind a négy szorzat osztható 25-tel, ami nem teljesülhet.
Emiatt a legnagyobb szám legalább 27. Legyen 27 a legnagyobb. Ezzel megnyílik egy kisebb mozgástér, elhagyhatjuk az előbbi 16 számból az egyiket, és az 5-tel oszthatók miatt a 25-öt ki kell venni. Az így adódó 16 szám elrendezhető a kívánt módon, ezt látjuk is az egyik táblázatban.
Több megoldó ismerte a feladat hátterét, megküldték ehhez ezeket az oldalakat is:
http://www.multimagie.com/indexengl.htm
https://oeis.org/A194941
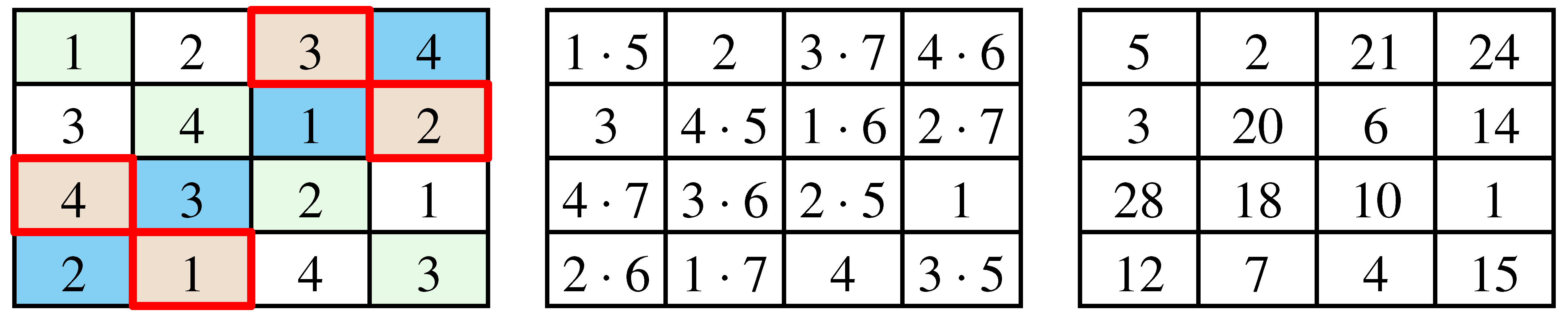
Szemerédi Ferenc az első táblázat egy-egy átlójában levő, illetve a pirossal keretezett mezőkben levő számokat szorozta meg rendre, 5-tel, 6-tal és 7-tel.
38. Egy négyzet alakú állami földterületet a privatizáció előtt felosztottak 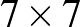 egybevágó parcellára az oldalakkal párhuzamos egyenesekkel. Az első szezonban 7 gazdálkodó vásárolt egy-egy parcellát úgy, hogy minden sor és minden oszlop csak egy privatizált parcellát tartalmazott. Minden következő szezonban mindegyik gazda vásárolhat egy újabb parcellát, ha az még nem volt privatizálva, és ha van közös oldala azzal a parcellával, amelyet az adott gazda az előző szezonban vásárolt.
egybevágó parcellára az oldalakkal párhuzamos egyenesekkel. Az első szezonban 7 gazdálkodó vásárolt egy-egy parcellát úgy, hogy minden sor és minden oszlop csak egy privatizált parcellát tartalmazott. Minden következő szezonban mindegyik gazda vásárolhat egy újabb parcellát, ha az még nem volt privatizálva, és ha van közös oldala azzal a parcellával, amelyet az adott gazda az előző szezonban vásárolt.
Megvásárolhatja-e 7 szezon alatt a 7 gazda mind a 49 parcellát?
A válasz: Nem lehetséges.
Megoldás. Ha 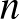 értéke páros, vagy ha
értéke páros, vagy ha 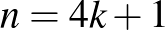 alakú, akkor az
alakú, akkor az 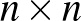 -es földterület minden parcellája megvásárolható
-es földterület minden parcellája megvásárolható 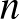 gazda által. Ezt látjuk
gazda által. Ezt látjuk 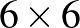 -os és
-os és 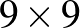 -es tábla esetén.
-es tábla esetén.
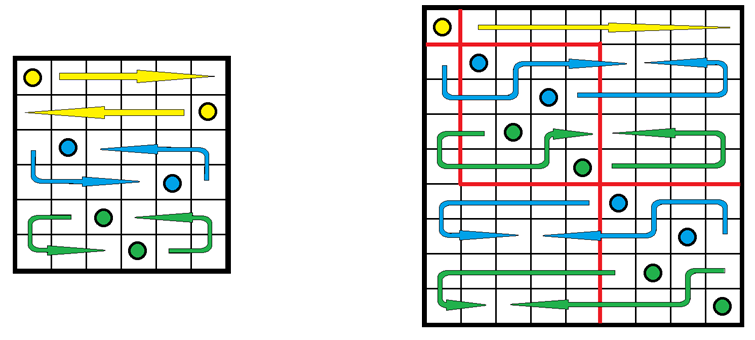
A 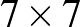 -es földterület minden parcellája – az adott feltételek mellett – nem privatizálható.
-es földterület minden parcellája – az adott feltételek mellett – nem privatizálható.
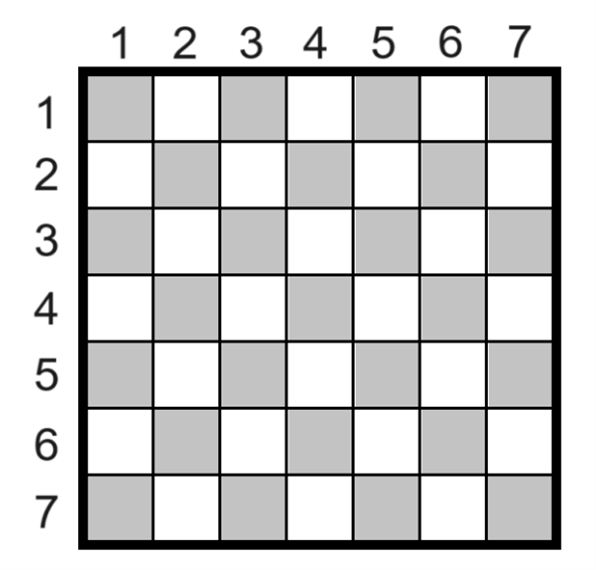
Színezzük a táblát az ábra szerint. A gazdák a következő szezonban mindig más színű parcellát vesznek, mint legutóbb.
Tegyük fel, hogy sikeres volt a privatizáció. Az első szezonban 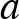 db fekete és
db fekete és 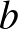 db fehér parcellát vettek. Akkor a 7 szezon alatt
db fehér parcellát vettek. Akkor a 7 szezon alatt 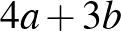 db fekete parcellát, és
db fekete parcellát, és 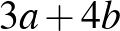 db fehér parcellát vesznek. A táblán 25 fekete és 24 fehér mező van, ezért
db fehér parcellát vesznek. A táblán 25 fekete és 24 fehér mező van, ezért  és
és 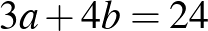 . Ezek különbsége:
. Ezek különbsége: 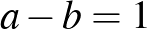 . Mivel
. Mivel 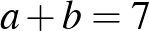 , így
, így 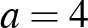 és
és 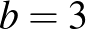 .
.
Lássuk be, hogy a táblán nem lehet 4 fekete és 3 fehér mezőt kiválasztani úgy, hogy minden sorból és minden oszlopból egy mezőt választunk.
A fekete mezők pozícióját megadó sor és oszlop sorszámának összege páros, a fehér mezőké páratlan. Adjuk össze az első szezonban vásárolt cellák pozícióját jelző számokat.
Mivel minden sorból és minden oszlopból egy cellát vásároltunk, így a pozíciószámok összege 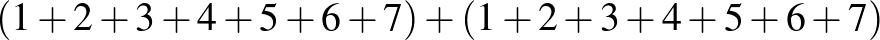 , és ez páros.
, és ez páros.
Ha 4 fekete és 3 fehér mező pozíciószámait adjuk össze, akkor 4 páros és 3 páratlan szám összegét kapjuk, ami páratlan.
A két eredmény nem egyezhet, hiszen egyik számolás szerint páros, a másik számítás szerint páratlan ez a szám. Tehát a sikeres privatizációhoz az első szezonban nem tudunk 7 alkalmas parcellát venni, így a feladat kérdésére „nem” a válasz.
Egy 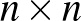 -es földterület minden parcellája pontosan akkor privatizálható
-es földterület minden parcellája pontosan akkor privatizálható 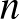 gazda által, ha
gazda által, ha 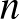 értéke nem
értéke nem 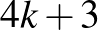 alakú.
alakú.
D&2d megoldása (részlet):
„Nem vásárolhatják meg mind a 49 parcellát a feltételeknek megfelelően.
Beszíneztem sakktábla-szerűen a parcellákat, lett 25 sötét, 24 világos. A második vásárlástól a hetedikkel bezárólag mindegyikük attól függetlenül, hogy az első vásárlás során milyen színű parcellát vásárolt meg, 3 sötét és 3 világos parcellát vásárolna, azaz összesen 21 sötét és 21 világos parcellát. Ez csak akkor lehetséges, ha kezdetben 4 sötét és 3 világos parcellát vásároltak, de ez nem lehetséges.”
Miért nem lehetséges? S. Ákos indoklása: A sorokat és oszlopokat koordinátázzuk a 0, 1, 2, ..., 6 számokkal. A sötét cellák koordináta-összege páros, a világos celláknál páratlan. Az első alkalommal mindegyik sorból és mindegyik oszlopból egy cellát választunk, ezek koordinátáinak összege 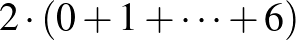 , ami páros. Azonban a 4 sötét és a 3 világos parcella koordináta-összegeinek összege páratlan, mert 4 páros és 3 páratlan számot adunk össze.
, ami páros. Azonban a 4 sötét és a 3 világos parcella koordináta-összegeinek összege páratlan, mert 4 páros és 3 páratlan számot adunk össze.
Dombi Péter megoldásából a megjegyzések:
1. Csak azt a tulajdonságot használtuk, hogy 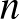 és
és 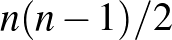 páratlan, így a fenti megoldás 7 helyett tetszőleges
páratlan, így a fenti megoldás 7 helyett tetszőleges 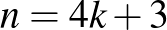 alakú számra is érvényes.
alakú számra is érvényes.
2. Minden más 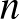 -re van olyan kiinduló helyzet, amelyre a feladat követelménye teljesíthető, ilyen példákat mutat a következő ábra, ha
-re van olyan kiinduló helyzet, amelyre a feladat követelménye teljesíthető, ilyen példákat mutat a következő ábra, ha 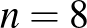 , 9, 10. A
, 9, 10. A 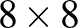 -as tábla bal és jobb felén jól látszik az az elrendezés, amivel
-as tábla bal és jobb felén jól látszik az az elrendezés, amivel 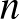 -ről
-ről 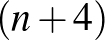 -re folytatható a minta mindhárom esetben.
-re folytatható a minta mindhárom esetben.
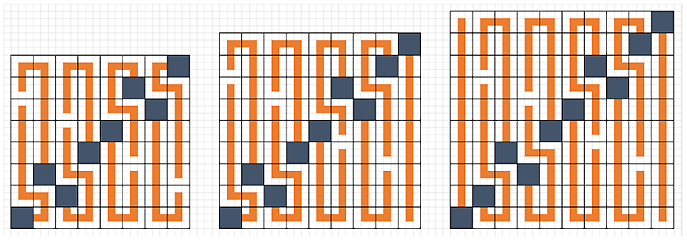
Folytatható földosztás 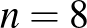 , 9, 10 esetén
, 9, 10 esetén
39. A Pinkerton Iroda nyomozója egy 20 embert érintő ügyet vizsgál. Azt tudja, hogy közöttük van a bűnös, és van közöttük egy szemtanú, de mindkettő személye kezdetben ismeretlen számára. A nyomozó minden nap meghívhat egy vagy több embert közülük, és ha a meghívottak között van a szemtanú, de nincs ott a bűnös, akkor hajlandó megszólalni a tanú, és elárulja neki, hogy ki a bűnös. A nyomozó legkevesebb hány nap alatt tudja biztosan megtalálni a bűnöst?
A válasz: 6.
Megoldás. Elegendő 6 nap ahhoz, hogy a 20 ember közül bármely kettőhöz, 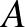 -hoz és
-hoz és 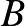 -hez legyen olyan nap, amikor
-hez legyen olyan nap, amikor 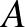 ott van a meghívottak között, és
ott van a meghívottak között, és 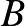 nincs ott; valamint van olyan nap is, amikor
nincs ott; valamint van olyan nap is, amikor 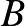 -t hívják, míg
-t hívják, míg 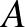 -t nem hívják, így lesz rá lehetőség, hogy a szemtanú elárulja a bűnöst.
-t nem hívják, így lesz rá lehetőség, hogy a szemtanú elárulja a bűnöst.
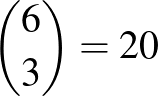 , ezért a 20 ember mindegyikéhez rendelhetünk egy egyedi azonosítót, egy 0-1 sorozatot, amely 3 db 0-ból és 3 db 1-esből áll. Az azonosítóban az 1-esek kijelölik azokat a napokat, amelyekre a meghívás szól. Ha
, ezért a 20 ember mindegyikéhez rendelhetünk egy egyedi azonosítót, egy 0-1 sorozatot, amely 3 db 0-ból és 3 db 1-esből áll. Az azonosítóban az 1-esek kijelölik azokat a napokat, amelyekre a meghívás szól. Ha 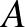 azonosítója
azonosítója 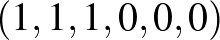 , akkor ő az első három napra kap meghívást.
, akkor ő az első három napra kap meghívást.
A 0-1 sorozatok megfeleltethetők egy 6 elemű halmaz 3-elemű részhalmazainak. Bármely két részhalmazhoz, 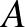 -hoz és
-hoz és 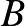 -hez van olyan
-hez van olyan 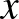 és
és 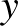 elem, hogy
elem, hogy 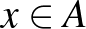 és
és 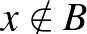 , valamint
, valamint 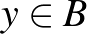 és
és 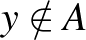 . Tehát bármely két emberhez van olyan nap, amikor az egyiket meghívják és a másikat nem, valamint ez felcserélve is teljesül.
. Tehát bármely két emberhez van olyan nap, amikor az egyiket meghívják és a másikat nem, valamint ez felcserélve is teljesül.
Látjuk, hogy 6 nap alatt kideríthető, ki a bűnös.
A meghallgatások alapján minden személyhez tartozik néhány nap, amelyekre ő meghívást kap. Így mindenkihez tartozik a napoknak egy részhalmaza. A részhalmazoktól elvárjuk, hogy ne legyen közöttük két olyan, hogy egyiknek a másik részhalmaza. Ezért a részhalmazok Sperner-rendszert alkotnak. Egy 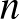 -elemű halmaz részhalmazaiból álló Sperner-rendszer legfeljebb
-elemű halmaz részhalmazaiból álló Sperner-rendszer legfeljebb 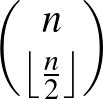 db halmazból állhat. Esetünkben
db halmazból állhat. Esetünkben 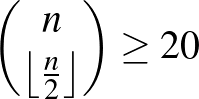 , ezért
, ezért 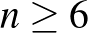 , azaz legalább 6 nap szükséges a meghallgatásokhoz.
, azaz legalább 6 nap szükséges a meghallgatásokhoz.
Makay Géza megoldása:
A 20 embert a kihallgatásoknak megfelelően bontsuk csoportokra. Minden emberhez jegyezzük fel, hogy melyik napon hívja be a nyomozó, jelöljük ezeket a halmazokat 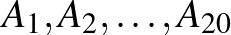 -szal. Ha
-szal. Ha 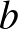 a bűnös és
a bűnös és 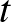 a tanú (
a tanú (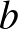 ,
, 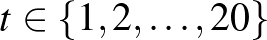 ), akkor annak kell teljesülnie, hogy
), akkor annak kell teljesülnie, hogy 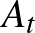 nem része
nem része 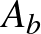 -nek, vagyis van olyan nap, amikor a tanú megjelenik, de a bűnös nem. Mivel nem ismerjük
-nek, vagyis van olyan nap, amikor a tanú megjelenik, de a bűnös nem. Mivel nem ismerjük 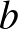 és
és 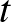 értékét, ezek a halmazok tehát nem tartalmazhatják egymást. Ha a napok száma
értékét, ezek a halmazok tehát nem tartalmazhatják egymást. Ha a napok száma 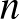 , akkor az
, akkor az 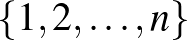 halmaz részhalmazairól beszélünk. Ezeknek a részhalmazoknak nem szabad, hogy túl kevés elemük legyen, mert az sok annál bővebb részhalmazban benne lesz és akkor azokat már nem tudjuk használni. De túl sok elemük sem lehet, mert azok sok kevesebb elemű részhalmazt zárnak ki. Ez alapján úgy tűnik, hogy optimális esetben
halmaz részhalmazairól beszélünk. Ezeknek a részhalmazoknak nem szabad, hogy túl kevés elemük legyen, mert az sok annál bővebb részhalmazban benne lesz és akkor azokat már nem tudjuk használni. De túl sok elemük sem lehet, mert azok sok kevesebb elemű részhalmazt zárnak ki. Ez alapján úgy tűnik, hogy optimális esetben ![$\left[\frac{n}{2}\right]$](/images/stories/latexuj/2024-12/2024-12-7tusa6megoldas/img51.png) elemű részhalmazokat kell tekinteni, azokból
elemű részhalmazokat kell tekinteni, azokból
![$\displaystyle \binom{n}{\left[\frac{n}{2}\right]}
$](/images/stories/latexuj/2024-12/2024-12-7tusa6megoldas/img52.png)
különböző van, és természetes módon egyik sem tartalmazza a másikat. Kis számolgatással kapjuk, hogy 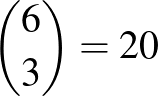 , tehát a nyomozó 6 nap alatt meg tudja találni a bűnöst úgy, hogy a 20 embert az
, tehát a nyomozó 6 nap alatt meg tudja találni a bűnöst úgy, hogy a 20 embert az 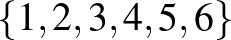 halmaz 20 darab háromelemű részhalmaza szerint osztja be napokra.
halmaz 20 darab háromelemű részhalmaza szerint osztja be napokra.
Belátjuk, hogy egy 5 napos kihallgatás-sorozattal a nyomozó nem feltétlenül kap a tanútól vallomást. Tekintsük a 20 ember egy 5 napos beosztását, és minden emberhez rendeljünk hozzá egy kettes számrendszerben felírt számot úgy, hogy a 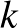 -adik helyiértéken pontosan akkor van 1-es, ha a
-adik helyiértéken pontosan akkor van 1-es, ha a 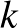 -adik napra az illetőt a nyomozó behívta. Két különböző emberhez nem rendelhetjük hozzá ugyanazt a számot, mert az azt jelentené, hogy a nyomozó őket pontosan ugyanazokra a napokra hívta be, és ha ők lennének a bűnös és a tanú, akkor a tanú nem fog beszélni. De az sem lehet, hogy ezen számok közül kettő csak egyetlen kettes számrendszerbeli számjegyben különbözzön, mert akkor egyetlen nap kivételével a két embert ugyanazokra a napokra hívta be a nyomozó, és ha azon a napon a bűnöst hívta be, akkor a tanú megint csak nem vall. Vagyis annak kell teljesülnie, hogy ezek a számok legalább két számjegyben különböznek. De ez sem lehetséges: ha elhagyom a számokból az egyik helyiértéken levő számjegyet, akkor négyjegyű kettes számrendszerbeli számokat kapok, amelyeknek különbözőeknek kellene lenniük, de azokból 16 darab van a 20 emberre. Ezzel beláttuk, hogy 5 nap alatt nem oldható meg az ügy.
-adik napra az illetőt a nyomozó behívta. Két különböző emberhez nem rendelhetjük hozzá ugyanazt a számot, mert az azt jelentené, hogy a nyomozó őket pontosan ugyanazokra a napokra hívta be, és ha ők lennének a bűnös és a tanú, akkor a tanú nem fog beszélni. De az sem lehet, hogy ezen számok közül kettő csak egyetlen kettes számrendszerbeli számjegyben különbözzön, mert akkor egyetlen nap kivételével a két embert ugyanazokra a napokra hívta be a nyomozó, és ha azon a napon a bűnöst hívta be, akkor a tanú megint csak nem vall. Vagyis annak kell teljesülnie, hogy ezek a számok legalább két számjegyben különböznek. De ez sem lehetséges: ha elhagyom a számokból az egyik helyiértéken levő számjegyet, akkor négyjegyű kettes számrendszerbeli számokat kapok, amelyeknek különbözőeknek kellene lenniük, de azokból 16 darab van a 20 emberre. Ezzel beláttuk, hogy 5 nap alatt nem oldható meg az ügy.
Hasonló okoskodással belátható, hogy 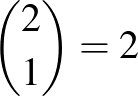 ember esetén 2 nap alatt mindkettőjüket egyszer-egyszer behívva tudja megoldani az ügyet. Persze az első nap után a nyomozó akkor is tudja, hogy ki a bűnös, ha nem a tanút hívta be, hiszen a bűnös nem beszél, és éppen ezért ő a bűnös. De a feladatot úgy értelmezve, hogy a bíró csak tanúvallomás alapján ítéli el a bűnöst, mindenképpen be kell hívnia a tanút is, tehát nem oldható meg egy nap alatt az ügy. És általában is igaz, hogy
ember esetén 2 nap alatt mindkettőjüket egyszer-egyszer behívva tudja megoldani az ügyet. Persze az első nap után a nyomozó akkor is tudja, hogy ki a bűnös, ha nem a tanút hívta be, hiszen a bűnös nem beszél, és éppen ezért ő a bűnös. De a feladatot úgy értelmezve, hogy a bíró csak tanúvallomás alapján ítéli el a bűnöst, mindenképpen be kell hívnia a tanút is, tehát nem oldható meg egy nap alatt az ügy. És általában is igaz, hogy ![$\binom{n}{\left[\frac{n}{2}\right]}$](/images/stories/latexuj/2024-12/2024-12-7tusa6megoldas/img55.png) ember esetén
ember esetén 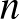 nap elegendő az ügy megoldásához,
nap elegendő az ügy megoldásához, 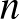 nap alatt minden embert
nap alatt minden embert ![$\left[\frac{n}{2}\right]$](/images/stories/latexuj/2024-12/2024-12-7tusa6megoldas/img51.png) különböző napra behívva. A fenti sorszámozás szerint
különböző napra behívva. A fenti sorszámozás szerint 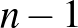 nap pedig akkor nem elég, ha
nap pedig akkor nem elég, ha
![$\displaystyle 2^{n-2}<\binom{n}{\left[\frac{n}{2}\right]}
$](/images/stories/latexuj/2024-12/2024-12-7tusa6megoldas/img57.png) ,
,ez pedig csak 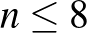 -ra teljesül. Ha pontosabb, és a „kimaradó” számokra is működő eredményt szeretnénk, akkor „nagyobb ágyúval” kell lőni erre a verébre.
-ra teljesül. Ha pontosabb, és a „kimaradó” számokra is működő eredményt szeretnénk, akkor „nagyobb ágyúval” kell lőni erre a verébre.
Sperner tétele kimondja, hogy egy 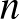 elemű halmazból legfeljebb
elemű halmazból legfeljebb ![$\binom{n}{\left[\frac{n}{2}\right]}$](/images/stories/latexuj/2024-12/2024-12-7tusa6megoldas/img55.png) olyan részhalmaz választható ki, amelyek páronként nem tartalmazzák egymást. Ennek következménye a konkrét feladatra, hogy legfeljebb ennyi ember esetén
olyan részhalmaz választható ki, amelyek páronként nem tartalmazzák egymást. Ennek következménye a konkrét feladatra, hogy legfeljebb ennyi ember esetén 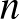 nap elegendő az ügy megoldásához. Például
nap elegendő az ügy megoldásához. Például 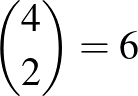 ember esetén 4 nap,
ember esetén 4 nap, 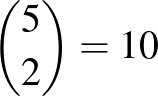 ember esetén 5 nap elegendő és kell is az ügy megoldásához.
ember esetén 5 nap elegendő és kell is az ügy megoldásához.
Egy érdekesség. Ha feltételezzük a feladat feltételei szerint, hogy a bűnöket minden bűnöző egyedül követi el, és miden bűntettnek van tanúja, akkor az összes, most élő ember által elkövetett bűntettet alig több, mint egy hónap alatt ki lehetne nyomozni. Valóban: 36 nap alatt 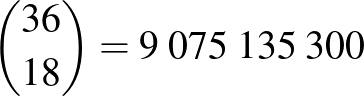 ember közül ki lehet választani bármelyik bűntett tettesét. Ez „párhuzamosan” is működik, hiszen bár egy tanú több bűnözőre is vallhat, de mivel mindig csak azokra vall, akik éppen aznap nincsenek jelen, ezért egy bűntett felderítése nem befolyásolja a többiét. Kicsit nehézkes ugyan minden nap a ma élő kb. 8,2 milliárd ember felét összehívni egy helyre és meghallgatni a potenciálisan több millió tanút, akik aznap éppen beszélhetnek, de ezek csak technikai részletkérdések: képzeljük el, hogy egyetlen nyomozó (kis matematikai segítséggel) napi akár több millió ügyet göngyölít fel és 100%-os felderítési aránnyal dolgozik ...
ember közül ki lehet választani bármelyik bűntett tettesét. Ez „párhuzamosan” is működik, hiszen bár egy tanú több bűnözőre is vallhat, de mivel mindig csak azokra vall, akik éppen aznap nincsenek jelen, ezért egy bűntett felderítése nem befolyásolja a többiét. Kicsit nehézkes ugyan minden nap a ma élő kb. 8,2 milliárd ember felét összehívni egy helyre és meghallgatni a potenciálisan több millió tanút, akik aznap éppen beszélhetnek, de ezek csak technikai részletkérdések: képzeljük el, hogy egyetlen nyomozó (kis matematikai segítséggel) napi akár több millió ügyet göngyölít fel és 100%-os felderítési aránnyal dolgozik ...
Dombi Péter megjegyzése: Ha 2 szemtanú volt ugyanilyen feltételekkel a 20 ember között, akkor elég 5 nap is. Kapjon mindenki két különböző napra meghívót a 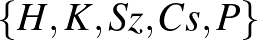 halmazból úgy, hogy minden párosítást pontosan 2 ember kapjon. Ez megtehető, mert
halmazból úgy, hogy minden párosítást pontosan 2 ember kapjon. Ez megtehető, mert 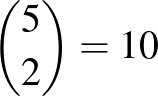 pár van, és jó is, mert ha a 2 szemtanú ugyanazt a párt kapja, akkor abban a párban valamelyik nap nem szerepel a bűnösnek osztott 2 nap között, ha pedig a szemtanúk különböző párt kapnak, akkor ők legalább három nap sorra kerülnek, tehát mindkét esetben legalább egyszer elkerülik a bűnöst.
pár van, és jó is, mert ha a 2 szemtanú ugyanazt a párt kapja, akkor abban a párban valamelyik nap nem szerepel a bűnösnek osztott 2 nap között, ha pedig a szemtanúk különböző párt kapnak, akkor ők legalább három nap sorra kerülnek, tehát mindkét esetben legalább egyszer elkerülik a bűnöst.
Udvari Tibor megoldása:
Nyilvánvaló, hogy egyesével meghallgatva őket, 20 nap alatt biztosan megtalálja a bűnöst. Ez azonban elég hosszú idő, érdemes rövidebb megoldást keresni.
Tegyük fel, hogy 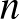 nap alatt lehet biztosan megtalálni a bűnöst. Ez úgy történik, hogy minden nap behív
nap alatt lehet biztosan megtalálni a bűnöst. Ez úgy történik, hogy minden nap behív 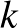 különböző embert. Arra kell figyelni, hogy ne legyen a 20 személy között két olyan, akik ugyanazokra a napokra kapnak meghívást. Ez elérhető, ha az
különböző embert. Arra kell figyelni, hogy ne legyen a 20 személy között két olyan, akik ugyanazokra a napokra kapnak meghívást. Ez elérhető, ha az 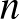 nap
nap 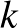 -elemű részhalmazaiból oszt ki 20-at a személyek között. Ehhez pedig arra van szükség, hogy a részhalmazok száma, ami
-elemű részhalmazaiból oszt ki 20-at a személyek között. Ehhez pedig arra van szükség, hogy a részhalmazok száma, ami  , legalább 20 legyen.
, legalább 20 legyen.
A binomiális együtthatók táblázatában 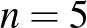 -ig csak 20-nál kisebb számok találhatók. Az
-ig csak 20-nál kisebb számok találhatók. Az 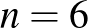 és
és 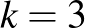 esetén viszont éppen 20 háromelemű részhalmaz van. Kapják tehát a személyek a meghívót a táblázatban megjelölt napokra.
esetén viszont éppen 20 háromelemű részhalmaz van. Kapják tehát a személyek a meghívót a táblázatban megjelölt napokra.
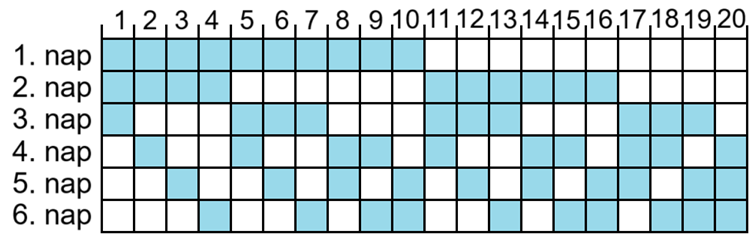
Így bármelyikük is a tanú, az ő három napja között biztosan találunk olyan napot, amikor nincs a bűnös is jelen a meghallgatáson.
Felvetődik a kérdés, hogy 5 nap alatt megtalálható-e a bűnös más módszerrel? Az előzőhöz hasonlóan soroljuk fel a napokat, amikor az egyes embereket behívja a nyomozó. Nem feltétlenül kell ugyanannyi napnak szerepelnie mindenkinél. Ha van két olyan halmaz a felsorolásban, amelyek közül az egyik részhalmaza a másiknak, akkor lehetséges, hogy a részhalmaz a tanú napjait, a másik a bűnös napjait adja meg. Ekkor a tanú hallgatni fog, mert minden alkalommal ott lesz a bűnös is. Tehát nem szerepelhet két olyan listája a napoknak, amelyek közül az egyik részhalmaza a másiknak. Összesen 31 nem üres részhalmaza lehet a napoknak. Nem lehet olyan, akit minden napra meghívtak, mert minden más kiosztás részhalmaza az övének. Nem lehet olyan, akit négy napon is meghívtak, mert 14 valódi, nem üres részhalmazt zárnánk így ki a továbbiakból, a maradék 16 nem elég a többi 19 személynek. Nem lehet olyan sem, akit csak egyetlen napon hívnak, mert így az ő napját tartalmazókat is ki kell zárni. Ezek száma 15, a többieknek megint nem jutna elegendő. Tehát csak két vagy három napon lehet egy-egy személyt meghívni. Ezekből pedig pont 20 van, minden személyre egy. De ha valakit csak két napon hívnak meg, akkor ki kell zárni az ő két napját tartalmazó háromnapos listákat, ezek száma pedig 3, így megint nem marad elég a többieknek. Három napos kiosztás pedig csak tíz van. Ezért 5 (vagy kevesebb) nap alatt nem lehet biztosan megtalálni a bűnöst.
Megjegyzés. Többen is megadták ezt az eljárást, amellyel 9 nap alatt megtaláljuk a bűnöst: Előbb 4 ötfős csoportra osztja az embereket. Az első 4 napon ezeket a csoportokat hallgatja ki. Ha a tanú nem nyilatkozott, akkor az egyik csoportban együtt van a bűnössel. Következő lépésben minden csoportból kiválaszt egy embert, így 5 négyfős csoportot kap, ahol biztosan nincs együtt a tanú a bűnössel. A legrosszabb esetben az utolsó, a 9. napon megtudja, hogy ki a bűnös.
Egy másik eljárás. Első nap hallgasson meg 10 embert, második nap a másik 10-et. Ha a szemtanú és a bűnös két különböző nap jött meghallgatásra, akkor megtalálja a nyomozó a bűnöst, tehát csak akkor nem találja meg, ha ugyanabban a 10-es csoportban voltak. Ezután mindkét 10-es csoportot bontsa két részre, és harmadik nap hallgassa meg mindkét csoport első felét, negyedik nap a második felét. Hasonlóképpen csak akkor nem találja meg a bűnöst, ha ugyanazon 5-ös csoportban voltak a szemtanúval. Ötödik nap hallgasson meg minden 5-ös csoportból 2-2 embert, hatodik nap a másik 3-3 embert. Csak akkor nem találja meg a bűnöst, ha ugyanazon 2-es vagy 3-as csoportban voltak a szemtanúval. Hetedik nap hallgasson meg a nyolc (2-es, illetve 3-as) csoportból 1-1 embert, nyolcadik nap még 1-1 embert. Csak akkor nem találja meg a bűnöst, ha a szemtanú a négy 3-as csoport valamelyikében van, kilencedik nap hallgassa meg ezeket, legkésőbb ekkor kiderül a bűnös.
40. Zsófi egy 12-oldalú szabályos sokszögbe egymás után átlókat húz be úgy, hogy minden újabb átló legfeljebb egy másik, korábban berajzolt átlót metszhet a sokszög belsejében. Legfeljebb hány átlót rajzolhat Zsófi?
A válasz: 18.
Megoldás. Belátjuk, hogy az 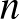 -oldalú szabályos sokszögbe a feltételek szerint legfeljebb
-oldalú szabályos sokszögbe a feltételek szerint legfeljebb 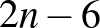 átló húzható be, azaz
átló húzható be, azaz 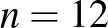 esetén legfeljebb 18 átló rajzolható.
esetén legfeljebb 18 átló rajzolható.
Ez az állítás 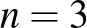 esetén nyilvánvaló.
esetén nyilvánvaló.
Indukciós lépés 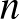 -re.
-re.
Az utolsónak berajzolt átló szétvágja a sokszöget egy 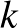 -oldalú és egy
-oldalú és egy 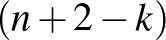 -oldalú sokszögre. Az utolsónak behúzott átló esetleg kettévág még egy átlót.
-oldalú sokszögre. Az utolsónak behúzott átló esetleg kettévág még egy átlót.
Az indukciós feltevés szerint a két részsokszögben a berajzolt átlók száma legfeljebb 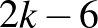 , illetve
, illetve 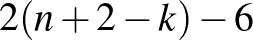 , ez összesen
, ez összesen 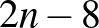 átló. Rajtuk kívül még berajzoltuk az utolsó átlót, és megrajzolhattuk a kettévágott átlót. Az átlók száma nem több
átló. Rajtuk kívül még berajzoltuk az utolsó átlót, és megrajzolhattuk a kettévágott átlót. Az átlók száma nem több 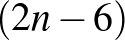 -nál.
-nál.
Az ábra mutatja, hogyan rajzolhat Zsófi 18 átlót a szabályos 12-szögbe.
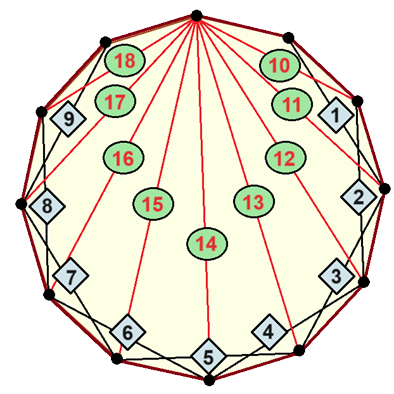
Másképp is be lehet látni, hogy a szabályos 12-szögbe legfeljebb 18 átlót rajzolhatunk. Színezzük az átlókat két színnel, kékkel és pirossal. Az elsőnek rajzolt átló kék. Ha az újonnan behúzott átló metsz egy korábban behúzottat, akkor azzal ellentétes színű lesz, ha nem metsz átlót, akkor ugyanolyan színű lesz, mint a legutóbb behúzott átló. A rajzolás befejeztével kapott kék átlók nem metszik egymást, és a piros átlók sem metszik egymást.
Hány átlót lehet berajzolni úgy, hogy azok páronként ne metsszék egymást?
A 12-oldalú sokszögbe berajzolt egymást nem metsző 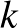 darab átló a sokszöget
darab átló a sokszöget 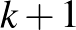 darab sokszögre vágja. Számoljuk össze a sokszögek oldalait! Az oldalak száma legalább
darab sokszögre vágja. Számoljuk össze a sokszögek oldalait! Az oldalak száma legalább 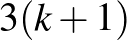 , másrészt ez a szám
, másrészt ez a szám 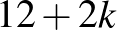 .
.
Mivel 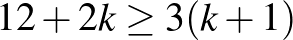 , így
, így 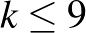 . Így a piros és kék átlók száma nem több
. Így a piros és kék átlók száma nem több 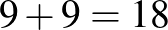 -nál.
-nál.
41. Pongrác, a kockafestő művész, egy kocka mindegyik lapját 64 darab egybevágó kis négyzetre osztotta, majd ezekből néhányat befestett, és közben arra is ügyelt, hogy ne legyen semelyik két befestett négyzet szomszédos. (Két négyzet szomszédos, ha van közös oldala; és ez a két négyzet lehet a kocka két különböző oldallapján is.) Legfeljebb hány négyzetet festhetett be Pongrác?
A válasz: 176.
Megoldás. A kocka mindegyik csúcsa körül kijelölünk négy darab, négyzetekből álló „körutat” úgy, ahogyan az ábra mutatja. Az azonos színnel jelölt körökön 3, 9, 15, illetve 21 négyzet van. Ezekből Pongrác legfeljebb 1, 4, 7, illetve 10 négyzetet festhet be.
Tehát az egy-egy csúcs körül kijelölt területen legfeljebb 22 négyzet festhető be, így a kocka felszínén legfeljebb 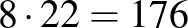 négyzetet festhet be Pongrác.
négyzetet festhet be Pongrác.
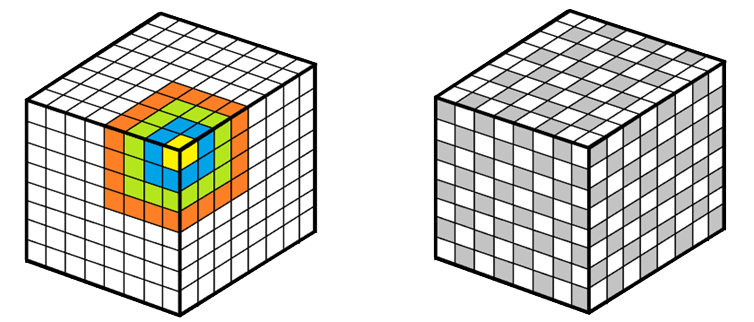
Ennyit valóban be is lehet festeni a következőképpen. A kocka két szemközti, alsó és felső lapján a második ábra szerint 24-24 négyzetet festünk be, a négy oldalsó lapon a sakktábla színezést követve 32-32 négyzetet. Ez összesen 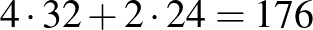 befestett négyzet. A befestett négyzetek között nincsenek szomszédosak.
befestett négyzet. A befestett négyzetek között nincsenek szomszédosak.

42. Egy távoli szigeten a lakosok egy része igazmondó, a többiek hazugok. Az igazmondók mindig igazat mondanak, a hazugok minden állítása hamis. Egy lakomán az egyik asztal körül 19-en ültek, akik a pohárköszöntő után mindnyájan azt állították, hogy mindkét szomszédjuk hazug. Sokan megsértődtek, a társaság egy része otthagyta az asztalt.
Akik maradtak, ezután már elégedetten nyugtázták, hogy mindkét szomszédjuk igazmondó.
– Valóban, most már nincs hazug köztetek – mondta vigasztalva őket a távozó társaság utolsó tagja.
Akik távoztak az asztaltól, leültek egy másik asztal köré, és itt mindenki azzal nyugtázta az új helyzetet, hogy a szomszédai között pontosan egy igazmondó van.
Hányan maradtak a helyükön ülve a társaság szétválása után?
A válasz: 7.
Megoldás. Az első állításokból következik, hogy sem két igazmondó, sem három hazug nem ülhet egymás mellett. Az igazmondók tehát a lakomán résztvevőknek legfeljebb a felét és legalább egyharmadát tették ki. Tehát 7, 8 vagy 9 igazmondó van közöttük.
A sértődöttek távozása után az állításokból két eset adódik az asztalnál maradókra:
(1) ha van köztük igazmondó, akkor mindannyian igazmondók (hiszen egy igazmondó mindkét szomszédja igazmondó), és az utolsóként távozó is igazmondó;
(2) mindannyian hazugok, és az utolsóként távozó is hazug.
Az új asztaltársaság állításai két esetben lehetnek érvényesek:
(A) mindannyian hazugok;
(B) felváltva egy hazug és két igazmondó ül.
Ha az (1) eset valósul meg, akkor a renegátok között van igazmondó, tehát az új asztalra a (B) leírás teljesül. Azaz a 19 fős társaságnak legalább a kétharmada igazmondó, és ez az igazmondók számára tett megállapításunk szerint nem lehetséges.
Ezért a (2) eset valósul meg, csak a hazugok maradtak a helyükön, a társaságban vannak igazmondók, így (B) szerint a távozók között pontosan kétszer annyi igazmondó volt, mint hazug. Ez csak akkor lehetséges, ha eredetileg 8 igazmondó van. Ők és 4 hazug távozott az első asztaltól, és 7 hazug maradt a helyén.
Izsák Beatrix megoldása:
7-en maradtak a helyükön. (Mind hazugok. A másik asztalnál 8 igazmondó van és 4 hazug.)
Eredetileg voltak hazugok és igazmondók is az asztalnál. Ez 19 lakosra, háromféleképpen lehet 12-7, vagy 11-8, vagy 10-9 a hazugok-igazmondók létszáma. Nem maradhattak csak igazmondók a régi asztalnál, mert akkor a távozó hazug igazat mondott volna. Így viszont igazmondó sem maradhatott a régi asztalnál. Tehát minden igazmondó átült. Ahhoz, hogy minden igazmondónak egy igazmondó szomszédja legyen 2 igazmondó mellé egy hazugnak kell eljönnie. Ez csak akkor teljesülhet, ha páros számú igazmondó volt. Azaz, ha eredetileg 8 igazmondó és 11 hazug volt. Így átült a 8 igazmondó és páronként közöttük egy hazug, összesen 4 hazug jött el. Azaz 7 hazug maradt a régi asztalnál.
Udvari Tibor megoldása:
Nézzük először az eredeti ülésrendet. Az összes igazmondó mindkét szomszédja csak hazug lehet. Három hazug pedig nem ülhet egymás mellett, legfeljebb kettő, akiknek a további szomszédai már igazmondók. Ez azt jelenti, hogy legalább 7 és legfeljebb 9 igazmondó lehetett a lakomán.
A kettévált társaság maradó részében ha volt igazmondó, akkor annak mindkét szomszédja igazmondó, de azok másik szomszédja is, és így tovább, tehát nem lehet hazug köztük. A maradók így vagy mind hazugok, vagy mind igazmondók. Az utoljára távozó a kijelentése alapján ekkor az első esetben szintén hazug, a másodikban pedig igazmondó. Így tehát a távozók között kell lennie az összes hazugnak és legalább egy igazmondónak, vagy az összes igazmondónak és legalább egy hazugnak.
Az eltávozott társaság minden igazmondó tagja mellett egy igazmondó és egy hazug ül. Ha több hazug ülne egymás mellett, akkor a két szélső hazug (mert másik szomszédjuk igazmondó) már igazat mondana, ami lehetetlen. A távozottak száma ezért 3-mal osztható, az igazmondók száma kétszerese a hazugokénak. Az eredeti társaságban a hazugok vannak többen, ezért nem lehet az, hogy ők mentek el mind. Az összes igazmondó elmenetele esetén csak akkor van feleannyi hazug, ha az igazmondók száma 8. Ekkor 4 hazug van közük, tehát a távozók száma 12. A helyükön maradtak száma így 7.
Róka Sándor,
a Héttusa rovat vezetője











