Információk

Főmenü

 Aktuális szám: 34. szám 2024. december 

Királynők a táblán

Királynők a táblán

A sakk a mai formájában a 15. században alakult ki Európában. Azóta sok alapvetően matematikai, a sakktáblát és -bábukat használó problémát találtak ki és oldottak meg. Az ilyen problémák többségében általában csak egy típusú bábu szerepel, és olyan kérdéseket feszegetnek, mint hogy egy ilyen bábuval körbe lehet-e menni szabályos sakklépésekkel a tábla összes mezőjén (Hamilton-út, vagy Hamilton-kör), hány ilyen bábu kell, hogy azok a tábla összes mezőjét üssék, vagy hogy hány helyezhető el belőlük úgy a táblán, hogy ne üssék egymást. Az Érintőben indított Héttusa rovatban (amelynek ebben a számban már a hetedik fordulójánál tartunk) is több ilyen jellegű feladat szerepelt.

Nemrégiben indult a Középiskolai Matematikai és Fizikai lapok oldalán egy fórum [1], ahol a Héttusa rovatban megjelent feladatokról lehet eszmét cserélni, vagy akár hasonló jellegű feladatokat kitűzni. Itt merült fel a következő kérdés: Legfeljebb hány királynő helyezhető el egy 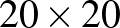$20\times 20$ mezős táblán úgy, hogy mindegyik legfeljebb egy másikat tartson ütés alatt? A kérdésre az interneten rákeresve gyorsan meg is találták a választ, 26 királynő helyezhető el [2], bár az ott található sorozatban minden királynőnek pontosan egy másikat kell ütnie. De az OEIS-en szinte minden sorozat megtalálható, az eredeti kérdésre is megvan a megfelelő sorozat [3], aszerint is 26 a válasz. Nézzük meg egy kis matematika segítségével, hogy honnan jön/jöhet ki ez a szám.

Először is belátjuk, hogy egy 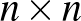$n\times n$-es táblán legfeljebb $[4n/3]$ királynő helyezhető el úgy, hogy mindegyik legfeljebb egy másikat tartson ütés alatt. Nézzük végig a lehetséges királynő-elhelyezési eseteket. Ha két királynő egy sorban vagy egy oszlopban üti egymást, akkor ezek miatt ki kell zárnunk a további királynő-elhelyezésből összesen 3 db sort vagy oszlopot: az első esetben 1 sort és 2 oszlopot, a második esetben 1 oszlopot és 2 sort. Ha egy királynőpár átlósan üti egymást, akkor azok miatt 2 sort és 2 oszlopot kell kizárnunk. Ha pedig egy királynő nem üt másik királynőt (így akkor persze azt sem üti királynő), vagyis „magányos”, akkor miatta 1 sort és 1 oszlopot kell kizárni. Ez alapján elég világos, hogy lehetőleg sorban és oszlopoban ütő királynőpárokat kellene leraknunk, hiszen azok királynőnként átlagban másfél sort vagy oszlopot zárnak ki, míg a másik két esetben kettőt. Ráadásul a sorban és oszlopban ütő királynőkből is kb. ugyanannyi párnak kell lennie, hiszen a sorok és oszlopok száma azonos, a párok pedig nem ugyanannyi sort, illetve oszlopot zárnak ki.

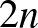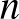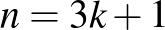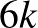Hány sorban, illetve oszlopban ütő királynőpárt rakhatunk le? Mivel a sorok és oszlopok számának összege $2n$, és egy pár ebből hármat foglal el, így legfeljebb $[2n/3]$ pár helyezhető így le. Ha $n$ 3-mal osztható, akkor ezzel minden sort és oszlopot „kihasználtunk”, nem lehet több királynőt elhelyezni, és $2[2n/3]=[4n/3]=4n/3$. Ha $n=3k+1$ alakú, akkor $[2n/3]=2k$ ilyen pár lesz, ami $6k$ sort-oszlopot foglal el az összesen 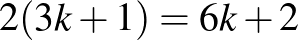$2(3k+1)=6k+2$-ből, tehát egy sor-oszlop pár még megmaradt egy magányos királynőnek, összesen tehát maximum $2k+1=[4n/3]$ királynőt helyezhetnénk el. 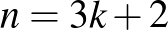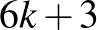Ha $n=3k+2$ alakú, akkor $[2n/3]=2k+1$ ilyen pár lesz, ami $6k+3$ sort-oszlopot foglal el az összesen 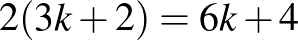$2(3k+2)=6k+4$-ből, a megmaradt egyetlen sorba vagy oszlopba több királynőt már nem tudunk lerakni, összesen tehát maximum $2k+1=[4n/3]$ királynőt helyezhetnénk el. 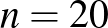Ezzel beláttuk, hogy $[4n/3]$ királynőnél többet nem tudunk lerakni (és ez az $n=20$ esetén pont 26-ot ad).

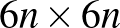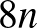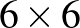Ezt a felső becslést meg is említik az OEIS oldalán [3], és hivatkoznak az IBM „Ponder this challenge” [4] megoldás oldalára [5], miszerint egy konstrukció bármilyen $6n\times 6n$-es tábla esetén $8n$ királynőt elhelyez. Ezen az oldalon konkrétan a $30\times 30$-as táblára mutatják meg a konstrukciót. Eszerint vegyük a feladatunk egy megoldását a $6\times 6$-os táblára, minden mezőt helyettesítsünk egy 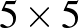$5\times 5$-ös táblával, és ahol eredetileg volt királynő, oda helyettesítsük be az 5-királynő probléma egyik rögzített megoldását. Az 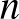$n$-királynő probléma [6] egyszerűbb (? ☺) a fentinél: egy 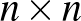$n\times n$-es táblán kell elhelyeznünk 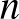$n$ királynőt úgy, hogy azok ne üssék egymást, és az ismert, hogy el lehet helyezni így a királynőket. Így a $30\times 30$-as tábla esetén a konstrukció így működik:

Lássuk, hogy miért is jó ez a konstrukció. Ezekből az elhelyezésekből indultunk ki:

Amikor a 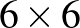$6\times 6$-os megoldásban két királynő egy sorban van, akkor a helyettük berakott 5-királynő megoldás megfelelő királynői azonos sorokba fognak kerülni, tehát ütik egymást. Ugyanez igaz oszlopokra is, vagyis mivel a 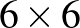$6\times 6$-os megoldásban minden királynő sorban vagy oszlopban üt egy másikat, ugyanez igaz lesz itt is. Ez viszont azt jelenti, hogy átlósan nem üthetnek a királynők, és ez egy nem triviális kérdés, hiszen 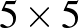$5\times 5$-ös táblázatokat helyettesítettünk be a 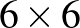$6\times 6$-os tábla mezői helyére. Nézzük meg a $30\times 30$-as táblán a felső 5 sorban levő királynőket. 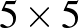Nyilván egy behelyettesített $5\times 5$-ös táblán a királynők nem üthetik egymást, hiszen az egy 5-királynő probléma megoldása. De a ferde ütésvonal most átnyúlik a szomszédba is (és persze még tovább is). Mit is jelent ez? Mivel ugyanazt a blokkot ismételtük meg a másik mellett, ezért úgy is mondhatnánk, hogy a királynők nem üthetnek úgy sem, hogy ha az ütésvonalak a függőleges oldalnál kimennének, akkor a másik oldalon jöjjenek be. Szemléletesen ez azt jelenti, hogy ha egy függőlegesen álló, 5 mezőszélesség alapkör kerületű hengerre feltekernénk a megoldást, akkor azon sem ütnének a királynők. Hasonlóan az első 5 oszlop alapján egy vízszintes tengelyű hengerre feltekerve a megoldást sem üthetnek a királynők. Vagyis a királynők egy tóruszon levő 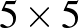$5\times 5$-ös táblán sem üthetik egymást. És ez most valóban teljesül is, könnyen ellenőrizhető.

Nézzünk tehát utána, hogy milyen 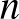$n$-ekre van megoldása az 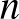$n$-királynő problémának tóruszon. Leggyakrabban Kløve [7] cikkére hivatkoznak, amelyben a szerző bebizonyítja, hogy csak 2-vel és 3-mal nem osztható 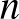$n$-ek esetén van megoldása a problémának. Már a cikk bevezetőjéből kiderül, hogy a szerző újnak gondolja eredményének a 3-mal nem osztható részét, de komolyabb utánajárással kiderül, hogy a problémát Pólya György már 1918-ban felvetette, és meg is oldotta [8]. Ez az eredmény viszont rossz hír nekünk: a fenti 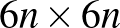$6n\times 6n$-es táblára vonatkozó konstrukció ezek szerint csak akkor működik, ha 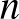$n$ nem osztható 2-vel vagy 3-mal. Valóban, próbáljuk ki 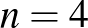$n=4$-gyel a konstrukciót, arra ugyanis csak egyetlen 4-kiránynő probléma megoldás létezik (tükrözéstől eltekintve), ez:

Ebből viszont ezt a táblát kapjuk:

És ez (természetesen) nem jó, vannak ferdén ütő királynők. Eszünkbe juthat, hogy megpróbáljuk a fordított behelyettesítést: a 4-kiránynő probléma megoldásába helyettesítsük be a 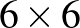$6\times 6$-os megoldásunkat. De az sem lesz jó, hiszen a 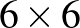$6\times 6$-os megoldás sem jó a tóruszon.

Ennyi negatívum után lássuk, hogy mi működik. Ilyen típusú feladatoknál, ahol minden természetes számra állítunk valamit, az embernek óhatatlanul eszébe kell jusson a teljes indukció. De ha eszébe is jut, ebben az esetben elég gyorsan el is veti, annyira nehéznek tűnik az indukció második lépése, amikor az előző természetes számokra feltett állításból kellene belátni az állítást a következő természetes számra. De azért valami ötletet lehet meríteni a teljes indukcióból: egy adott megoldásból kiindulva néhány lépést azért meg tudunk tenni.

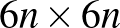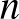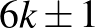$6n\times 6n$-es táblán a fenti konstrukció megfelelő királynő-elhelyezést ad, ha az $n$ szám $6k\pm 1$ alakú, vagyis 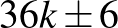$36k\pm 6$ oldalhosszú táblákra van megoldásunk. Mivel a 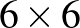$6\times 6$-os megoldásból indulunk ki, amelyikben sem a főátlóban, sem a mellékátlóban nincs királynő, ezért az így megkonstruált megoldásokban sem lesz. Márpedig akkor legalább két lépést tovább tudunk menni.

Ha van egy megoldásunk egy 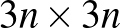$3n\times 3n$-es táblára, amelyikben a főátlóban nincs királynő, akkor azt kiegészítve a jobb oldalon és lent egy oszloppal, illetve sorral, és azok metszéspontjába lerakva egy királynőt, kapunk egy megoldást a  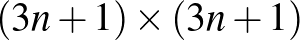$(3n+1)\times(3n+1)$-es táblára. Ha van egy megoldásunk egy 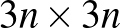$3n\times 3n$-es táblára, amelyikben a főátlóban és a mellékátlóban sincs királynő, akkor azt kiegészítve a jobb és bal oldalon egy-egy oszloppal és lent két sorral, akkor azokban a főátlóba és a mellékátlóba egy sorba lerakva egy-egy királynőt, kapunk egy megoldást a  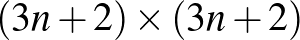$(3n+2)\times(3n+2)$-es táblára. Az alábbi ábrák szemléltetik ezeket a megoldásokat:

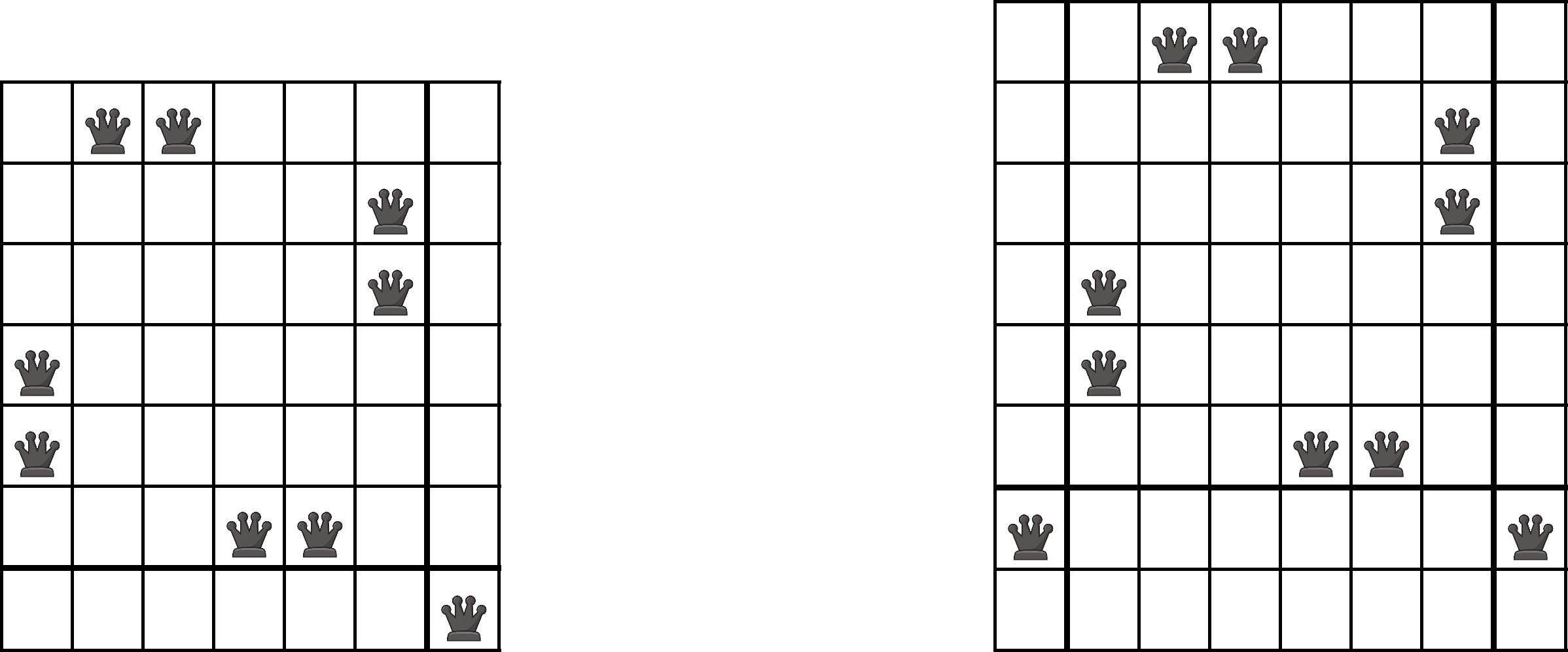
De tovább is mehetünk a 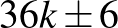$36k\pm 6$-os táblára konstruált megoldásainkból. A tóruszon tekintett 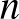$n$-királynő problémára egy egyszerű megoldás ([7], [8]), hogy az 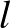$l$-edik sorban a 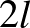$2l$-edik oszlopba helyezzük el a királynőt (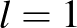$l=1$, 2, …, 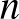$n$). Természetesen, mivel tóruszon vagyunk, ha 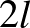$2l$ nagyobb, mint 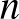$n$, akkor a 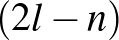$(2l-n)$-edik oszlopról beszélünk. A fenti 5-királynő problémára pontosan ezt a megoldást használtuk fel a $30\times 30$-as táblán, és itt a példa a 7-, a 11- és a 13-királynő problémára:

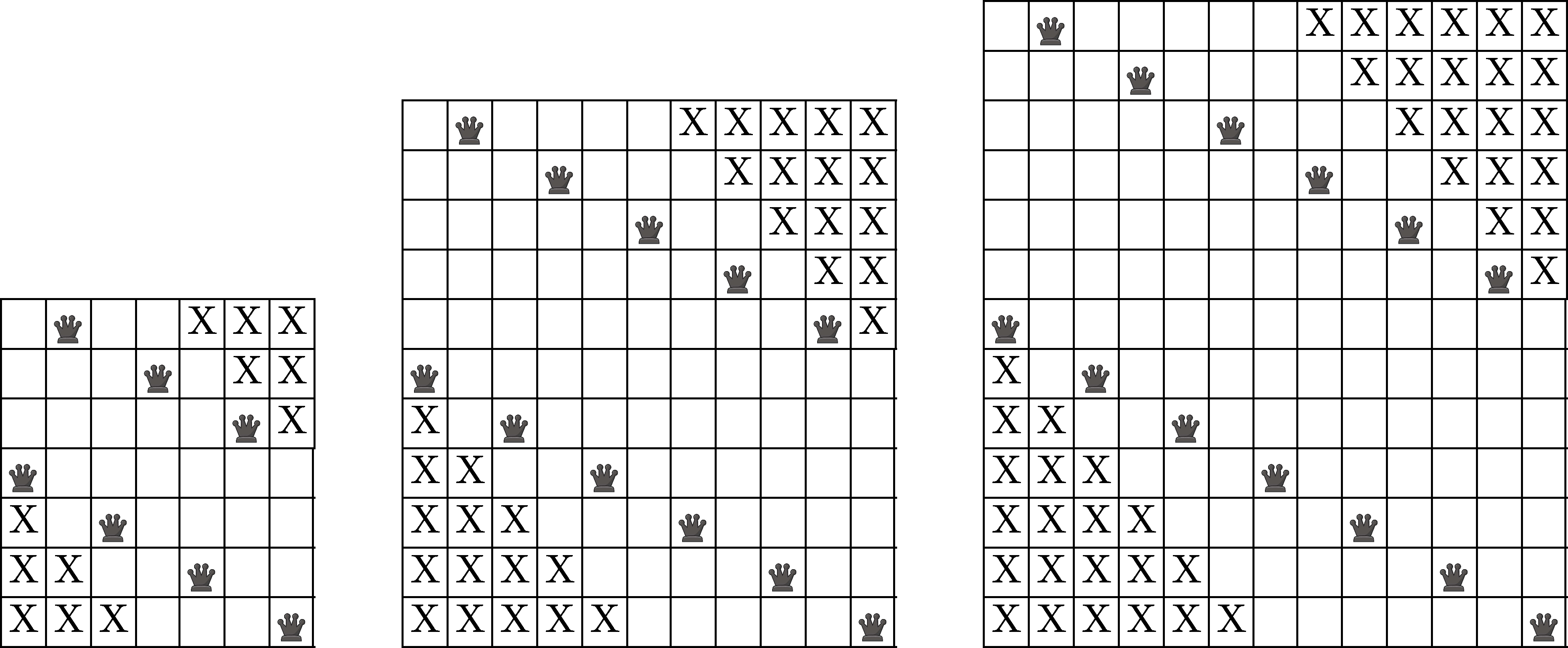
Könnyen ellenőrizhető, hogy 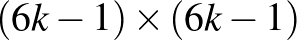$(6k-1)\times(6k-1)$-es tábla esetén a bal alsó és jobb felső sarkoktól legfeljebb 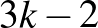$3k-2$ Manhattan-távolságra (oszlop sorszámok különbsége plusz sor sorszámok különbsége) levő mezőkön nincs királynő. 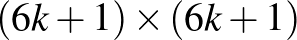$(6k+1)\times(6k+1)$-es tábla esetén ezek a bal alsó és jobb felső sarkoktól legfeljebb 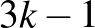$3k-1$ Manhattan-távolságra levő mezők. Másképpen mondva a főátlóval párhuzamos bal alsó és jobb felső sarkokon átmenő és azokhoz elegendően közeli ferde vonalakon nincsenek királynők (ezeket a fenti ábrákon X-szel jelöltük). Ez azt jelenti, hogy az ezek alapján a 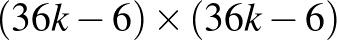$(36k-6)\times(36k-6)$-os és 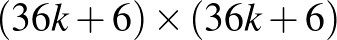$(36k+6)\times(36k+6)$-os táblára konstruálható megoldásokban a főátlóban és az alatta és felette párhuzamos 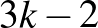$3k-2$, illetve 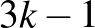$3k-1$ darab vonalon nem lesz királynő. Az is látható, hogy mivel a 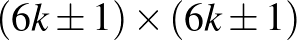$(6k\pm 1)\times(6k\pm 1)$-es táblákon a bal felső sarokban nincs királynő, ezért a 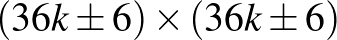$(36k\pm 6)\times(36k\pm 6)$-os táblákra kapott megoldásban a mellékátlóban és a vele alatta párhuzamos vonalon sem lesz királynő.

Próbáljuk meg az így kapott megoldásainkat kiegészíteni sorokkal és oszlopokkal, és azokba úgy elhelyezni a királynőket, hogy azok a korábban elhelyezett királynőket ne üssék, és egymás között is legfeljebb egy másikat üssenek. Mivel csak azt akarjuk kihasználni, amit az előző bekezdésben beláttunk, szimmetriától eltekintve alapvetően háromféle módon egészíthetjük ki a táblázatunkat:

1.  minden sort, illetve oszlopot a táblázat alá és tőle jobbra helyezzük el,

2.  minden sort a táblázat alá helyezzük el, oszlopokkal bal és jobb oldalon is kiegészítjük a táblázatot,

3.  nincs megkötés: új sorok vannak a táblázat alatt és felett is, új oszlopok a táblázattól jobbra és balra is.

Vegyük észre, hogy az első esetben a kiegészítő részben csak az eredeti táblázatban nem szereplő sorokba és oszlopokba rakhatunk királynőket, így annak a kiegészítő résznek önmagában is megoldásnak kell lennie a problémánkra. A harmadik eset azért nem optimális, mert mint tudjuk, a mellékátló mentén összesen csak két vonal szabad, nem érdemes a bal alsó és a jobb felső saroknál is kiegészítő mezőket pazarolni, hiszen ezekre a vonalakra legfeljebb 2 királynőt helyezhetünk el, az pedig egyetlen oszloppal is megoldható. Az egyetlen – esetleg előnnyel kecsegtető – megoldás tehát a második lehet, ahol (a nagy táblázat miatt) a „szétválasztott” oszlopok között a ferde ütésvonalak „szétesnek”, nem fognak átütni a másik oldalra. És az előző megjegyzés alapján a bal alsó saroknál levő kiegészítő rész csak 1 oszlopot fog tartalmazni, amelyiknek királynő fog állni a felső két mezőjében, így (csak a táblázat alja van az ábrán):

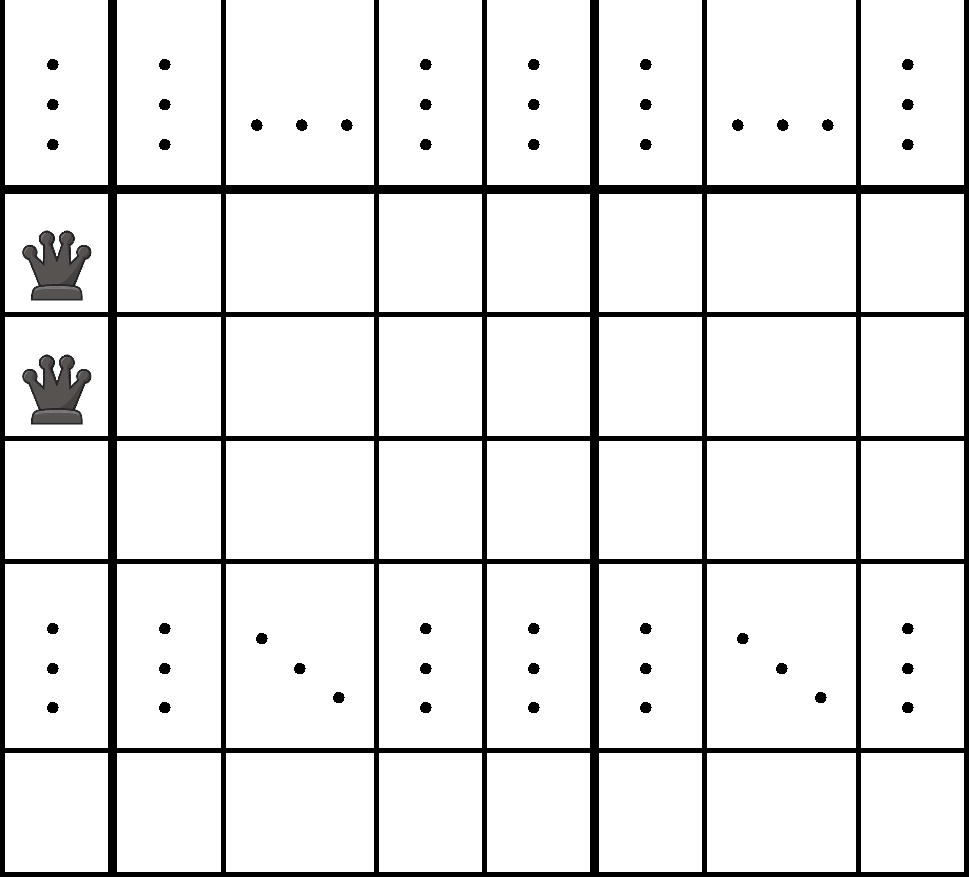
Mivel 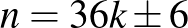$n=36k\pm 6$ oldalhosszú táblákra van megoldásunk, a kiegészítéssel csak az egyik ilyen megoldástól kell elérnünk a következőig. Vagyis, ha van ilyen „kiegészítő táblás” megoldás 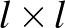$l\times l$-es táblákra, ahol 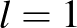$l=1$, 2, …, 23, akkor nagy 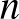$n$-ekre megoldottuk a problémát. Azért csak nagy 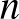$n$-ekre, mert a főátló mentén csak elegendően nagy 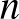$n$-ekre van „hely” a kiegészítő táblának, hogy ferde ütések se legyenek.

Keressünk tehát kiegészítő táblákat 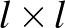$l\times l$-es méretben, ahol 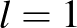$l=1$, 2, …, 23. Az 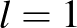$l=1$, 2 esetet már megoldottuk fent, a többi kifejezetten a számítógépnek való, de persze sok számolással járó feladat, tehát használjuk ki, amit eddig megtudtunk. Tudjuk, hogy két királynőt a bal oldali oszlopban a felső sarokba kell helyezni, és hogy ezek ferde ütései nem érnek át a jobb oldalra. Igen lényeges szempont, hogy kiegészítő táblás megoldást keresünk, hiszen 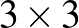$3\times 3$-as táblán nem lehet 4 királynőt elhelyezni, de kiegészítő táblás megoldás mégis van: a bal felső sarokban 2 királynő függőlegesen és a jobb alsó sarokban két királynő vízszintesen. Tudjuk, hogy érdemes a sorban és oszlopban levő királynőpárokat felváltva elhelyezni, hiszen azokból kb. ugyanannyinak kell lenni még a kiegészítőtáblás megoldásban is. Érdemes magán a (félig) kitöltött táblázaton kívül soronként és oszloponként tárolni a még szabad mezőket, hogy ne kelljen keresgélni, hová lehet még királynőket elhelyezni. Fejeljük meg még ezt azzal, hogy igyekezzünk úgy elhelyezni a királynőket, hogy az újabb pár minél kevesebb eddig még nem ütött mezőt üssön. És persze a backtracking algoritmus működik itt is. Ha mindezt belevesszük a programba, akkor kb. 70 másodperc alatt megvan az eredmény: 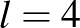$l=4$, 6, 7 esetén nincs kiegészítő táblás megoldás, minden más esetre van. Valahol ez nem meglepő eredmény: kis táblák esetén a tábla méretéhez viszonyítottan túl sok mezőt foglalnak el a ferde ütések.

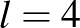Akkor hogy is állunk? Hiányzik az $n=36k+6+l$ eseteknél az $l=4$, 6, 7, de ez megoldható úgy, hogy a 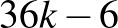$36k-6$ esetből indulunk ki és 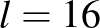$l=16$, 18, 19-es kiegészítő táblát használunk. Hiányzik viszont a 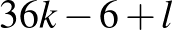$36k-6+l$ szintén az 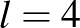$l=4$, 6, 7 esetekre. Mivel van megoldásunk az eredeti problémára az 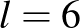$l=6$, 7 esetre, azokat a megoldásokat a fenti 1. pont szerint a táblázat jobb alsó sarkához illesztve kapunk megoldást. A megmaradt 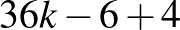$36k-6+4$-es eset 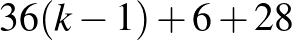$36(k-1)+6+28$ alakú is, vagyis találnunk kellene 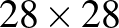$28\times 28$-as kiegészítő táblát is. Sajnos az eddigi optimalizálások/gyorsítások nem elegendőek: a program órákig futott anélkül, hogy eredményre jutott volna. Próbáljuk ki a mohó algoritmust: ne is próbáljunk ki olyan királynőpárokat, amelyek a minimálisnál több mezőt ütnek. Kiderül, hogy ezzel túl mohók voltunk, nem találjuk meg az összes létező kiegészítő táblás megoldásokat. De megtehetjük, hogy olyan királynőpárokat próbálunk csak ki, amelyek a minimálisnál csak 1-2 mezővel többet ütnek, és ez utóbbi esetben már megtaláljuk az összes megoldást az 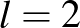$l=2$, …, 23 esetre is. Futtassuk a programnak ezt a változatát az 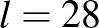$l=28$ esetre, és pár perc alatt kapunk megoldást [9].

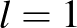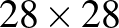Mivel csak $l=1$, 2, …, 28-as kiegészítő táblákkal sikerült megoldanunk az összes esetet, ezért csak $k\geq 10$-re lesz elég hely egy $28\times 28$-as kiegészítő táblának is, és így 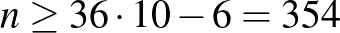$n\geq 36\cdot 10-6=354$-től van meg a konstrukció a megoldásokra. 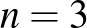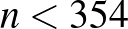Persze jónéhány kisebb számra is működik a konstrukció, de nem mindenre, és mivel $n=3$, 4, 5 esetén sem tudunk elhelyezni $[4n/3]$ darab királynőt a táblára megfelelően, ezért valóban kérdés, hogy mit tudunk $n<354$-re. De mivel (az eddigiek alapján) a kis táblákkal van csak probléma, az a sejtés, hogy 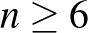$n\geq 6$-ra van megoldás.

Makay Géza,
Szegedi Tudományegyetem, Matematikai Intézet

 

Hivatkozások

[1] https://www.komal.hu/forum?a=to&tid=365
[2] https://oeis.org/A051754/a051754%5F1.pdf
[3] https://oeis.org/A260113
[4] https://research.ibm.com/haifa/ponderthis/challenges/August2008.html
[5] https://research.ibm.com/haifa/ponderthis/solutions/August2008.html
[6] https://hu.wikipedia.org/wiki/Nyolckir%C3%A1lyn%C5%91-probl%C3%A9ma
[7] Kløve, T.: The modular 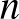$n$-queen problem, Discrete Mathematics, Vol. 19, No. 3 (1977), pp. 289–291 https://www.sciencedirect.com/science/article/pii/0012365X77901108
[8] Pólya, Gy.: Über die „doppelt-periodischen” Lösungen des 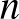$n$-Damen-Problems. In Mathematische Unterhaltungen und Spiele, W. Ahrens, Ed., Teubner, Leipzig, 1918, pp. 364–374. https://archive.org/details/in.ernet.dli.2015.211707/page/n373/mode/2up
[9] https://www.math.u-szeged.hu/%7Emakay/kiegtab.txt

 

Ezt a kutatást a TKP2021-NVA-09 projekt támogatta. A TKP2021-NVA-09 számú projekt a Kulturális és Innovációs Minisztérium Nemzeti Kutatási Fejlesztési és Innovációs Alapból nyújtott támogatásával, a TKP2021-NVA pályázati program finanszírozásában valósult meg.