Bevezető gondolatok
A magyarországi matematikának egyik kiemelkedő területe a gráfelmélet. A nemzetközi szakkönyvekben, példatárakban nagyon gyakran találkozhatunk hivatkozásokkal magyar matematikusok tételeire, hazánkban kitűzött versenyfeladatok bemutatásával. Ezek a példák megmozgatják a fiatalok fantáziáját, hiszen a problémák megoldása szinte minden esetben valamilyen speciális felismerésen, különleges fogalomtársításon alapul, így komoly szellemi kihívást jelent még a matematikailag képzettek számára is.
Az iskolai tanórákon a diákok többsége általában csak a legalapvetőbb megoldási lehetőségekkel ismerkedik meg, és egyszerű feladatok megoldására válik alkalmassá. A tanulók rutinszerű példákat oldanak meg, adott tulajdonságú egyszerű gráfokat hoznak létre, és vizsgálják a létezés feltételeit. Ebben a cikkben más szempontok szerint vizsgáljuk meg a gráfokat. Áttekintjük, hogy a gráfok milyen széles körben lehetnek segítségünkre a problémák megoldásában. Tesszük ezt a színek segítségével úgy, hogy kiderüljön, hogy egy ilyen szemléltetéssel még a nehezebb feladatok is könnyebben megoldhatóvá válnak. Elkalandozunk a játékok, a sík- és a kombinatorikus geometria, a poliéderek, a versenyek világába, foglalkozunk optimális útvonalak, elhelyezkedések, kapcsolatrendszerek kialakításával. Eközben találkozunk a gráfelmélet legfontosabb összefüggéseivel, a fokszámokra vonatkozó ismeretekkel, a Turán-tétellel, a fákkal, a síkgráfokkal, az Euler-féle poliédertétellel, a Ramsey-problémákkal és a versenygráfokkal.
Az egyes módszerek segítségével nagyon változatos nehézségű és érdekes feladatok megoldását mutatjuk meg. A cikk végén azt is bemutatjuk, hogy hogyan készíthetünk mi magunk is nevezetes tételek segítségével feladatokat mások számára. Összességében egy jól hasznosítható anyagot szeretnénk adni a kollégáknak az iskolai szakköri munkához.
A cikkben a következő fogalmakat ismertnek tekintjük: gráf, teljes gráf, körmentes gráf, reguláris gráf, izolált pont, csúcs fokszáma.
A cikkben említett tételek bizonyítása megtalálható ezekben a művekben: Katona Gyula–Recski András–Szabó Csaba: A számítástudomány alapjai, Xiong Bin–Zheng Zhongyi: Graph Theory.
1. Gráfok alkalmazása nem várt helyzetekben
A következő két feladat arra mutat be egy-egy példát, hogy mennyire eredményesen használhatók a gráfok a játékelméletben. Segítségükkel tudatosan, gyorsan alakíthatunk ki egy játékhelyzetet, és könnyen indokolhatóvá válik az is, ha egy állás nem hozható létre.
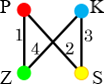
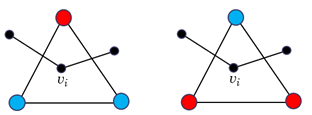
Egy \(3\times 3\)-as négyzetrács négy sarokmezőjében a bal oldali ábra szerint két világos és két sötét huszár áll. A huszároknak a sakk szabályai szerinti mozgatásával elérhető-e, hogy a bábuk a jobb oldali ábra szerinti helyzetbe kerüljenek, ha a lépések során a bábuk csak üres mezőkre ugorhatnak?

Megoldás:
Számozzuk meg a négyzetrács mezőit az alábbi ábra szerint:
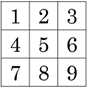
Rendeljük hozzá a rács négyzeteihez egy gráf \(v_1\), \(v_2\), …, \(v_9\) csúcsait, és kössük össze éllel azokat a csúcsokat, amelyekhez tartozó mezők elérhetők egymásból egy lóugrással. Ekkor a huszárok kezdeti és végső helyzetét is bejelölve az alábbi \(G_1\) és \(G_2\) gráfokat kapjuk:
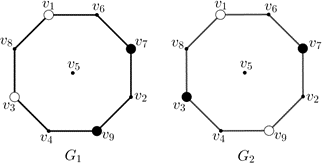
Mivel a huszároknak megfelelő csúcsokat a mozgatás mindig csak szomszédos üres csúcsba viheti, ezért a forgásirány szerinti sorrendjük a lépegetések során nem változhat meg.
Így a fehér–fehér–fekete–fekete huszár helyzete nem változhat át fehér–fekete–fehér–fekete sorrendre. Tehát a kívánt állapot nem érhető el.
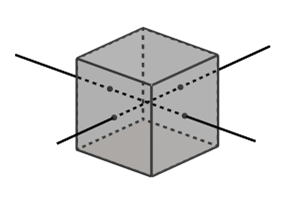
Egy 4 kockából álló logikai építőjáték elemeinek lapjai az alábbiak szerint vannak színezve:
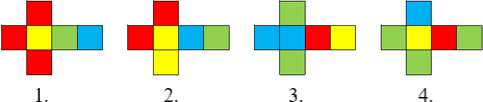
A játék célja az, hogy a kockákból úgy építsünk 4-szintes tornyot, hogy annak minden oldallapján az összes szín előforduljon.
Megoldás:
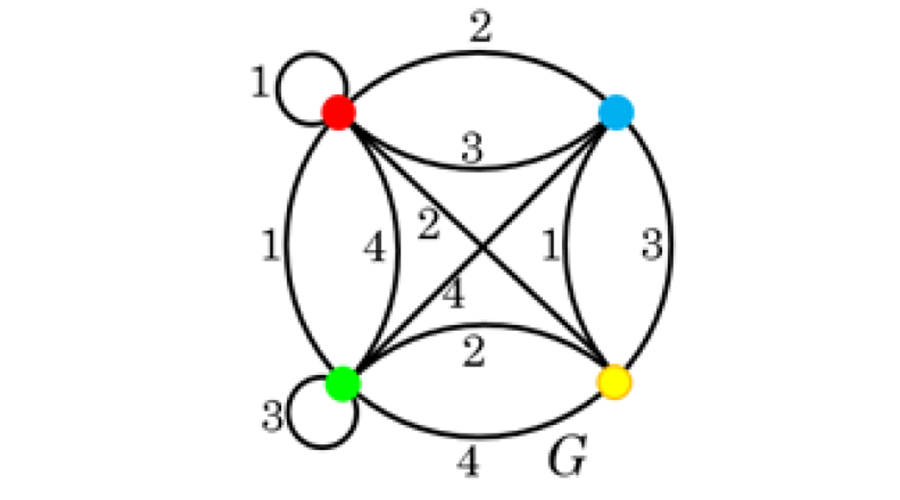
Rendeljünk az egyes kockákhoz egy-egy gráfot úgy, hogy ezen a kockák lapjainak a színezését át tudjuk tekinteni. Az egyes gráfoknak legyen négy csúcsa a négy színnek megfelelően. Két csúcs között akkor haladjon él, ha a kocka két szemben lévő lapja ilyen színű. Ha két ilyen lap azonos színű, akkor ezt az ábrán hurokél jelöli. Négy csúcsból és 3 élből álló gráfokat kapunk:
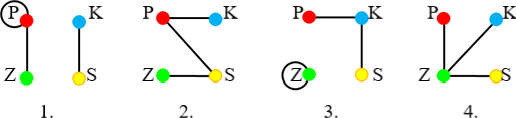
A négy gráfot egyesítve az alábbi \(G\) gráf adódik. Minden élre ráírjuk, hogy melyik kockából került az egyesített gráfba.
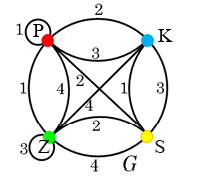
A feladat megoldásához olyan \(G_1\), \(G_2\) részgráfokat keresünk, amelyek megadják azokat a színeket, amelyek a torony elején-hátulján, illetve bal és jobb oldalán szerepelnek. \(G_1\), \(G_2\) kiválasztásának szempontjai:
– A torony felépítésében mind a 4 kocka részt vesz, ezért \(G_1\) és \(G_2\) minden számozott gráfnak egy élét tartalmazza.
– A hasáb oldallapjain minden szín előfordul, ezért \(G_1\) és \(G_2\) pontjai a \(P\), \(K\), \(Z\) és \(S\) csúcsok.
– A hasáb szemközti oldallapjain minden szín egyszer-egyszer, összesen kétszer szerepel, ezért a csúcsok másodfokúak, \(G_1\) és \(G_2\) 2-regulárisak.
Egy lehetséges megoldás:
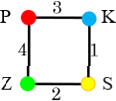 |
 |
| \(G_1\) | \(G_2\) |
| Elöl – hátul | Balra – jobbra |
A két gráf mindegyikén szerepel az 1, 2, 3, 4 szám. Ez azt jelenti például, hogy az 1-es kockát úgy tegyük magunk elé, hogy elöl legyen a kék, hátul a sárga (vagy fordítva), balra legyen a piros, jobbra a zöld (vagy fordítva). A 2-es, 3-as, 4-es kocka elhelyezését hasonlóan olvashatjuk le a \(G_1\), \(G_2\) gráfokról. A második kocka elhelyezésétől kezdve figyelnünk kell arra, hogy azonos oldalra ne kerüljön kétszer egy szín. A kockát megfelelő tengelye/tengelyei körül elforgatva ez a probléma megoldható.
Ha ilyen módon felépítettünk egy tornyot, akkor a kockák sorrendje függőlegesen tetszőlegesen permutálható.
Az alábbi torony ilyen elvek szerint épült:
 |
hátsó lap | bal oldali lap | |
| 4. kocka | P | Z | |
| 3. kocka | K | K | |
| 2. kocka | Z | S | |
| 1. kocka | S | P |
2. Csúcsok fokszámának vizsgálata
Felhasznált tételek:
T1: Ha egy \(G\) gráfban a \(v_1\), \(v_2\), …, \(v_n\) ( \(n\in \mathbb{N}^+\)) csúcsok fokszámai rendre \(d(v_1)\), \(d(v_2)\), …, \(d(v_n)\) és az élek száma \(e\) ( \(e\in \mathbb{N}\)), akkor \[\displaystyle d(v_1)+d(v_2)+\ldots+d(v_n)=2e.\] T2: Bármely \(G\) gráfban a páratlan fokú csúcsok száma páros.
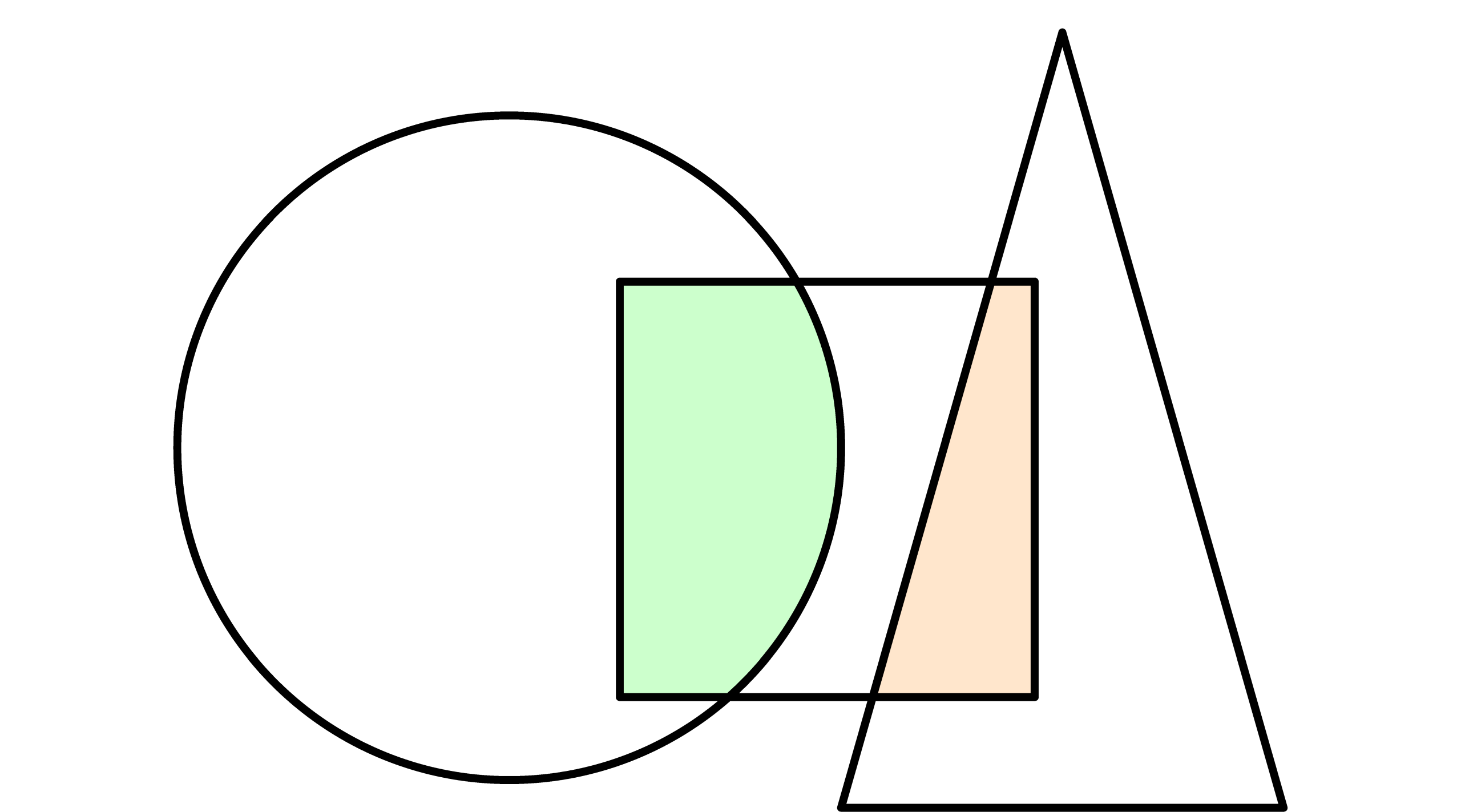
Egy háromszög csúcsai piros, kék és zöld színekkel vannak kiszínezve. A nagy háromszög belsejében elhelyezünk néhány pontot, és így azt több kisebb háromszögre bontjuk. Két kis háromszögnek lehet közös csúcsa, közös oldala, vagy lehetnek közös pont nélküliek is. A kis háromszögek csúcsait is kiszínezzük a piros, kék vagy zöld színek valamelyikével. Bizonyítsuk be, hogy bármilyen színezés esetén kapunk olyan háromszöget, amelynek csúcsai különböző színűek.
Megoldás:
Válasszunk ki egy pontot (\(v_1\)) a nagy háromszögön kívül, és kössük össze azt a nagy háromszög piros-kék oldalára illeszkedő részháromszögének egy belső pontjával (\(v_2\)). Továbbá keressük meg belül az összes piros-kék végpontú oldalt, és kössük össze az azokra illeszkedő két háromszögnek egy-egy belső pontját egy-egy szakasszal [az ábra szerint \((v_3;v_4)\), \((v_4;v_5)\), \((v_5;v_6)\)].
Tekintsük a kiválasztott \(v_i\) pontokat egy \(G\) gráf csúcsainak, a berajzolt szakaszokat \(G\) éleinek.
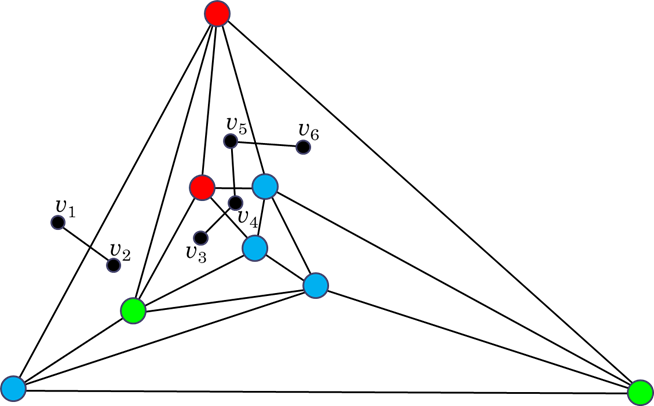

\[G\] Ekkor a \(G\) gráf azon belső csúcsai, amelyek foka 1 és a nagy háromszög belsejében találhatók, egy háromszínű háromszög belsejében vannak.
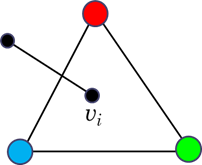
Másrészt \(G\) azon belső csúcsai, amelyek foka 2, egy piros-kék háromszög belsejében helyezkednek el.
\(G\) csúcsainak fokszámát vizsgálva, mivel a nagy háromszögön kívüli csúcs foka 1, és a gráfban a páratlan fokú csúcsok száma páros, ezért \(G\) tartalmaz még legalább egy 1-fokú csúcsot. A korábbi megállapításunk szerint ez a pont egy háromszínű háromszög belsejében helyezkedik el.
3. Turán-tétel
Egyszerűbb formában:
Ha egy \(n\) csúcspontú \(G\) gráfban nincs \(K_{k+1}\) (teljes \((k+1)\)-es), akkor éleinek száma legfeljebb \[\displaystyle \frac{k-1}{2k}n^{2}.\]
Teljes formában:
Ha \(n=kq+r\), ahol \(0\leqslant r<k\) (\(r\), \(q\in \mathbb{N})\), és az \(n\) csúcspontú \(G\) gráfban nincs \(K_{k+1}\), akkor az élek \(e\) számára teljesül, hogy \[\displaystyle e\leqslant \frac{k-1}{2k}n^{2}-\frac{r(k-r)}{2k}.\]
Az egyenlőség olyan \(T(n, k)\) Turán-gráfra teljesül, amely \(k\) közös elem nélküli \(A_1\), \(A_2\), …, \(A_k\) ponthalmazból áll, ahol \(\vert A_1\vert=\ldots=\vert A_r\vert=q+1\), \(\vert A_{r+1}\vert=\ldots=\vert A_k\vert=q\), és két pontot pontosan akkor kötünk össze, ha azok különböző ponthalmazokhoz tartoznak.
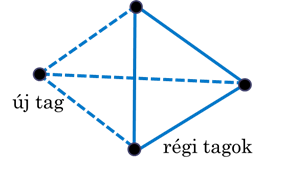
Egy bridzsklubnak van egy speciális szabálya, amely szerint 4 tag csak abban az esetben játszhat együtt, ha a párokon belül egyik játékos sem volt korábban a párjának partnere.
Egy találkozón 14 tag jelent meg, akik közül mindenki korábban 5 társának volt partnere. Az est folyamán 3 mérkőzés lejátszása után a tagok szomorúan tapasztalták, hogy a klubszabály miatt be kell fejezniük a játékot. Már készülnek a befejezésre, amikor beállít egy új tag, akit egyikük sem ismer. Mutassuk meg, hogy az ő érkezésével még legalább egy játék lejátszható.
Megoldás:
Rendeljük hozzá az eredetileg jelen levő 14 taghoz egy \(G\) gráf egy-egy csúcsát. Kössük össze éllel azokat a csúcsokat, amelyekhez tartozó emberek még nem volt partnerei egymásnak, majd vizsgáljuk a gráf \(\bar{G}\) komplementerét.
Figyelembe véve, hogy a 14 személy mindegyikének korábban 5 partnere volt, és az est folyamán az új tag érkezéséig már 3 mérkőzést lejátszottak, ezért \(\bar{G}\) éleinek száma: \[\displaystyle e\left(\bar{G}\right)=\frac{14\cdot 5}{2}+3\cdot 2=41\text{, és}\] \[\displaystyle e(G)=e\left(K_{14}\right)-e\left(\bar{G}\right)=\frac{14\cdot 13}{2}-41=50.\]
Az új tag érkezésével akkor nyílik lehetőség új partira, ha \(G\) tartalmaz háromszöget. A Turán-tétel alapján, ha \(G\)-ben nincs \(K_3\), akkor \[\displaystyle e(G)\leqslant \frac{k-1}{2k}\cdot n^{2}=\frac{{14}^{2}}{4}=49.\]
Mivel \(G\)-ben az élek száma meghaladja a 49-et, így \(G\) tartalmaz háromszöget. Ehhez a háromszöghöz tartozó személyek és az új tag között tehát lebonyolítható a szabályoknak megfelelő mérkőzés.
4. Fagráfok
Fontosabb definíciók, tételek:
D1: Az összefüggő, körmentes gráfokat fáknak nevezzük.
T1: Minden legalább 2 pontú \(T\) fagráfban van legalább 2 elsőfokú pont.
T2: Ha a \(T\) fagráf csúcsainak száma \(n\) ( \(n\in \mathbb{N}^+\)), akkor éleinek száma \(e=n-1\).
T3: Legyen a \(T\) fagráf csúcsainak száma \(n\), éleinek száma \(e\). Ekkor az alábbi tulajdonságok ekvivalensek egymással:
a) \(T\) fagráf,
b) \(T\) körmentes és \(e=n-1\),
c) \(T\) összefüggő és \(e=n-1\).
Egy \(n\) csúcsú teljes gráf éleit Dia és Viki a megadott sorrend szerint felváltva színezi ki pirosra. Az veszít, aki először hoz létre piros kört. Melyik lánynak van nyerő stratégiája?
Megoldás:
A feladatban szereplő játéknak csak \(n\geqslant 3\) esetén van értelme, hiszen \(n=1\), \(n=2\) esetén senki sem veszít, tehát a játék döntetlen eredménnyel ér véget.
Használjuk fel a feladat megoldásához az alábbi két gráfelméleti tételt:
– Egy \(n\) csúcsú összefüggő gráfnak legalább \(n-1\) éle van.
– Egy \(n\) csúcsú körmentes gráfnak legfeljebb \(n-1\) éle van.
Azt fogjuk belátni, hogy \(n\geqslant 3\) esetben helyes játék esetén az veszít, akinek az \(n\). élt kell pirosra színeznie. Állításunk igazolásához elég belátni, hogy ha \(k<n\), akkor az a játékos, aki a \(k\) élt színezi, még meg tudja tenni, hogy ne ő hozzon létre piros élekből álló kört.
Tekintsük azt a \(G_{k-1}\) gráfot, amit az addig kiszínezett \(k-1\) él alkot az \(n\) csúccsal.
Ha \(k<n\), akkor \(k-1<n-1\), így \(G_{k-1}\) nem összefüggő. Ez azt jelenti, hogy szétbomlik két vagy több \(T_1\), \(T_2\), …, \(T_j\) fára, amelyek között nem fut él.
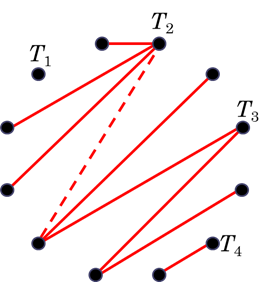
\(k=9\)
Az éppen következő játékosnak nem kell mást tennie, mint két fa egy-egy pontját kell összekötnie egy piros éllel. Ha \(G_{k-1}\)-ben nem volt piros kör, akkor \(G_k\)-ban sem lesz, mivel a kör kialakításához fel kellene használni az újonnan behúzott élt, illetve a két fa között kellene lennie még egy összekötő élnek. Ilyen pedig nincs.
Így beláttuk, hogy ha az egyik leánynak a \(k<n\) sorszámú élt kell kiszíneznie, akkor el tudja kerülni a piros kör kialakulását. Az a játékos viszont, akinek az \(n\). él jut, ezt már nem tudja megtenni. Ezért helyes stratégia esetén páros \(n\)-re Dia, páratlanra pedig Viki nyer.
5. Euler-vonal
Felhasználható definíciók, tételek:
D1: Vonalnak nevezzük egy gráf éleinek egymáshoz csatlakozó sorozatát, amelyben minden él legfeljebb egyszer szerepelhet, de lehetnek olyan pontok, amelyek többször is előfordulnak.
D2: Euler-vonalnak nevezünk egy gráfban egy vonalat, ha az a gráf minden élén áthalad. Az Euler-vonal lehet nyitott, ha a kezdő- és végpontja nem azonos, és lehet zárt, ha kezdő- és végpontja megegyezik.
T1: Izolált pontot nem tartalmazó gráfban akkor és csak akkor van zárt Euler-vonal, ha a gráf összefüggő és minden pont fokszáma páros.
T2: Izolált pontot nem tartalmazó gráfban akkor és csak akkor van nyitott Euler-vonal, ha a gráf összefüggő és két pont fokszáma páratlan, a többi pont fokszáma páros.
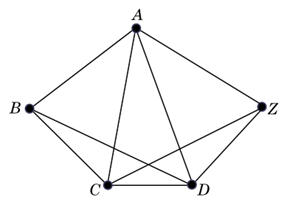
Az ábra szerint Atom Anti és Zé, a két hangya az \(A\) és \(Z\) pontokban állnak. Azt mondja Anti Zé-nek: „Versenyezzünk, nézzük meg, hogy melyikünk halad át először a 9 élen és ki ér előbb a \(B\) csúcsba.” A két hangya egyszerre indul, és azonos sebességgel halad. Ki nyeri meg a versenyt?
Megoldás:
Tekintsük a pontokat egy \(G\) gráf csúcsainak, a köztük húzott szakaszokat pedig az éleinek. \(G\) összefüggő, és az egyes csúcsok fokszámai: \(d_Z=d_B=3\), \(d_A=d_C=d_D=4\).
Tehát \(G\)-ben pontosan két páratlan fokú csúcs van (\(B\) és \(Z)\). Így T2 alapján a gráfban van nyílt Euler-vonal, amelynek két végpontja \(B\) és \(Z\).
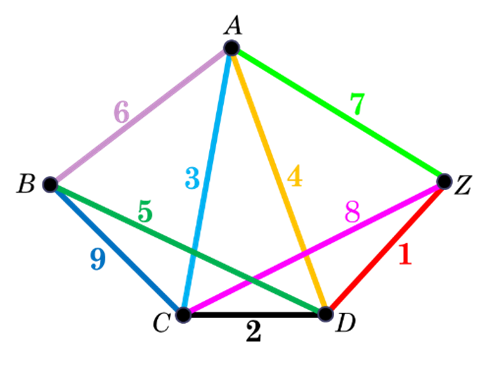
Ezért, ha Zé például \(Z\)-ből indulva a \(ZDCADBAZCB\) nyílt Euler-vonalon halad, akkor 9 él érintésével eljuthat \(B\)-be (lásd a fenti ábrát). Anti a páros fokszámú \(A\) pontból indul, így ő nem juthat el élismétlés nélkül \(B\)-be. Tehát a megfelelő útvonalválasztás esetén Zé nyeri meg a versenyt.
6. Hamilton-kör
Fontosabb definíciók, tételek:
D: Egy \(G\) gráfban egy kört Hamilton-körnek nevezünk, ha \(G\) minden pontját pontosan egyszer tartalmazza.
T1 (Ore-tétel): Legyen \(G\) egyszerű gráf csúcsainak száma \(n\) ( \(n\geqslant 3\), \(n\in \mathbb{N}^+\)). Ha bármely \(v\), \(v’\) nem szomszédos csúcspár esetén \(d(v)+d(v’)\geqslant n\), akkor \(G\) tartalmaz Hamilton-kört.
T2 (Dirac-tétel): Legyen \(G\) egyszerű gráf csúcsainak száma \(n\) ( \(n\geqslant 3\), \(n\in \mathbb{N}^+\)). Ha a gráfban minden pont foka legalább \(n/2\), akkor a gráfban létezik Hamilton-kör.
Egy kör alakú asztal körül legalább 5 ember ül. Lehetséges-e, hogy úgy módosítsuk az ülésrendet, hogy mindenkinek két új szomszédja legyen?
Megoldás:
5 fő esetén egy lehetséges megoldás:
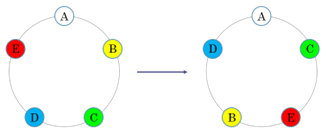
5-nél több személy esetén rendeljük a társaság tagjaihoz egy gráf csúcsait, és kössük össze éllel azokat a csúcsokat, amelyekhez tartozó emberek az eredeti helyzet szerint nem voltak szomszédok. Így olyan \(G\) gráfot kapunk, amelyben minden csúcs foka \(\left\vert V(G)\right\vert-3=n-3\) ( \(n\geqslant 6\), \(n\in \mathbb{N}^+\)). Ekkor a gráfban bármely két csúcs fokszámának összege \(2n-6\).
\(n\geqslant 6\) esetén \(2n-6\geqslant n\), és az Ore-tétel miatt \(G\) tartalmaz Hamilton-kört. Ez alapján alakítható ki a helyes ülésrend. Az ábra \(n=6\) esetén mutatja be a megoldást:
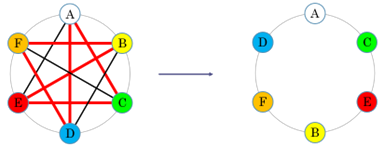
7. Síkba rajzolható gráfok
D: Egy gráf síkba rajzolható, ha lerajzolható a síkban úgy, hogy élei kizárólag a csúcspontokban találkoznak.
Euler-formula: Ha adott egy véges összefüggő síkgráf, ahol \(c\) a csúcsok, \(e\) az élek, \(l\) pedig a tartományok számát jelöli, beleértve a külső nagy területet is, akkor \[\displaystyle c+\ell=e+2\]
Adott egy körön \(n\) pont (\(n>3\), \(n\in \mathbb{N}^+\)). Bármelyik két pontot összekötjük egy-egy szakasszal. Ezen szakaszok között nincs 3 olyan, amelyek a körön belül egy pontban metszik egymást. Határozzuk meg a körön belül kialakult tartományok számát.
Megoldás:
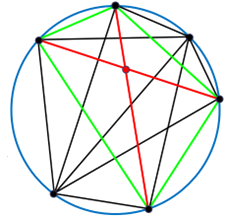
A kör \(n\) ívének eltávolítása után egy egyszerű síkgráfot kapunk, amelynek csúcsai a körön levő pontok és a szakaszok körön belüli metszéspontjai.
A körön levő pontok közül bármelyik 4 pontosan egy belső metszéspontot határoz meg, így \[\displaystyle c=n+\binom{n}{4}.\]
A körön levő pontok mindegyikéhez \(n-1\), a belső pontokhoz 4-4 él tartozik, és minden élnek két végpontja van, ezért \[\displaystyle e=\frac{1}{2}\cdot \left[n(n-1)+4\binom{n}{4}\right].\]
A síkgráfokra vonatkozó Euler-formula alapján a tartományok száma: \[\displaystyle \ell’=e+2-c=\left[\frac{n\left(n-1\right)}{2}+2\binom{n}{4}\right]+2-\left[n+\binom{n}{4}\right].\]
Az így kimaradt tartományokhoz hozzáadva a körívek által határolt \(n\) tartományt és levonva a körön kívüli részt: \[\displaystyle \ell=\ell’+n-1=\frac{n\left(n-1\right)}{2}+\binom{n}{4}+1=\binom{n}{2}+\binom{n}{4}+1.\]
8. Ramsey-számok
Fontosabb ismeretek:
T (Ramsey-tétel): Adott \(k\) és \(p\) pozitív egészekhez létezik egy olyan legkisebb \(r(k;p)\) szám, hogy bármely \(n\geqslant r(k;p)\) \((n\in \mathbb{N}^+)\) esetén az \(n\) pontú \(K_n\) teljes gráf éleit két színnel – kékkel és pirossal – kiszínezve van a gráfban egy kék \(K_k\) vagy egy piros \(K_p\).
T1: \(r(k;1)=r(1;p)=1\)
T2: \(r(k;2)=k\), \(r(2;p)=p\)
T3: \(r(k;p)\leqslant r(k-1;p)+r(k;p-1)\)
T4: (Erdős–Szekeres): \(r(k;p)\leqslant \dbinom{k+p-2}{k-1}\)
Néhány Ramsey-szám: \[\displaystyle r(3;3)=6, \quad r(3;4)=9, \quad r(3;5)=14, \quad r(4;4)=18, \quad r(4;5)=25.\]
Az 1, 2, 3, 4, 5 számokat véletlenszerűen két csoportba (\(A\) és \(B\)) osztjuk. Bizonyítsuk be, hogy az egyik csoportba kerül két olyan szám, amelyek különbsége megegyezik a csoport egyik számával.
Megoldás:
Az \(i=1, 2, 3, 4, 5, 6\) számokhoz rendeljük hozzá egy \(G\) gráf \(v_i\) csúcsait. Bármely \(1\leqslant i<j\leqslant 6\) esetén kössük össze a \(v_i\), \(v_j\) csúcsokat kék éllel, ha \(j-i\in A\), és pirossal, ha \(j-i\in B\). Így egy kétszínű \(K_6\) teljes gráfot kapunk, amely \(r(3;3)=6\) miatt tartalmaz monokromatikus háromszöget. Legyenek ennek csúcsai \(v_i\), \(v_j, v_k\) ( \(1\leqslant i<j<k\leqslant 6\)). Ekkor az \(a=j-i\), \(b=k-j\), \(c=k-i\) számok egy csoportban vannak, és \[\displaystyle c-b=(k-i)-(k-j)=j-i=a.\]
Például \(A=\{1; 3\}\), \(B=\{2; 4; 5\}\) esetén:
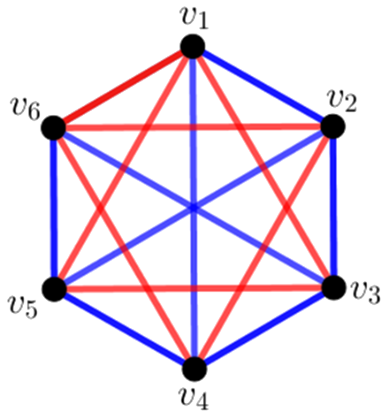
Piros háromszög \(v_1v_3v_5\), (\(3-1=5-3=2\), \(5-1=4\)) és \(4\in B\), \(2\in B\) és \(4-2=2\in B\).
9. Versenygráfok
Fontosabb ismeretek:
D: Egy gráfot irányított versenygráfnak nevezünk, ha \(n\) ( \(n\geqslant 2\), \(n\in \mathbb{N}^+\)) csúcsot tartalmaz, és bármely két csúcsot pontosan egy irányított él köt össze.
Jelölése: \(\overrightarrow{K}_n\).
Az él a győztestől mutat a vesztes felé.
A \(v\) csúcs kifoka az adott csúcsból kiinduló, befoka pedig az oda befutó élek száma. Jelölésük: \(d^+(v)\), illetve \(d^{-}(v)\).
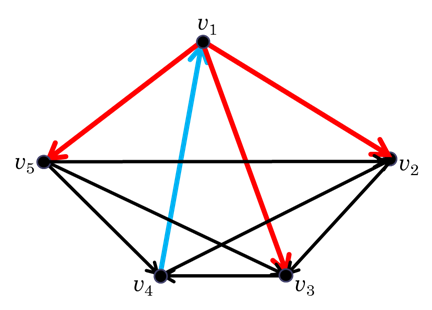
T1: Legyenek \(v_1\), \(v_2\), …, \(v_n\) egy \(\overrightarrow{K}_n\) versenygráf csúcsai. Ekkor \[\displaystyle d^+\left(v_1\right)+d^+\left(v_2\right)+\ldots+d^+\left(v_n\right)=d^{-}\left(v_1\right)+d^{-}\left(v_2 \right)+\ldots+d^{-}\left(v_n\right)=\frac{n(n-1)}{2}.\]
T2: Egy versenygráfban mindig létezik olyan csúcs, ahonnan vezet irányított út bármely más csúcsba. Az ilyen utak maximális hossza 2.
T3: A \(\overrightarrow{K}_n\) versenygráf mindig tartalmaz \(n-1\) hosszú Hamilton-utat.
T4: Egy \(\overrightarrow{K}_n\) versenygráf ( \(n\geqslant 3\), \(n\in \mathbb{N}^+\)) akkor és csak akkor tartalmaz kört, ami háromszög, ha létezik két olyan \(v\) és \(v’\) csúcs, melyekre teljesül, hogy \[\displaystyle d^+(v)=d^+\left(v’\right).\]
A tételek alapján nagyon könnyen készíthetünk magunk is versenyfeladatokat. A feladatok megoldása a tételek bizonyítása szerint történik, amelyekre a cikk terjedelme miatt nem térünk ki. Lássuk tehát a versenyeken kitűzhető, nem túl könnyű példákat!
Egy egyfordulós körmérkőzéses tornán \(n\) ( \(n\geqslant 2\), \(n\in \mathbb{N}^+\)) játékos vesz részt, és mindenki a többiekkel egy-egy mérkőzést játszik. A mérkőzéseken nincs döntetlen eredmény. Bizonyítsuk be, hogy a versenyzők között van olyan személy, hogy ő, az általa legyőzött személyek és az általa legyőzött személyek által legyőzött ellenfelek az összes sportolót tartalmazzák.
Megoldás: T2-ből következik az állítás.
Egy asztalitenisz tornán bármely két játékos pontosan egyszer játszik a többi versenyzővel. Bizonyítsuk be, hogy a játékosokat lehet úgy sorszámozni, hogy minden játékos legyőzte a közvetlenül utána következőt.
Megoldás: T3-ból következik az állítás.
Egy körmérkőzéses egyfordulós röplabda tornán \(n\) ( \(n\geqslant 3\), \(n\in \mathbb{N}^+\)) csapat vesz részt. A tornán egyetlen csapat sem győzte le az összes ellenfelét. Bizonyítsuk be, hogy a résztvevők között található három olyan \(A\), \(B\), \(C\) csapat, hogy \(A\) legyőzte \(B\)-t, \(B\) legyőzte \(C\)-t és \(C\) legyőzte \(A\)-t.
Megoldás: A skatulyaelvből és T4-ből következik az állítás.
Ez az írás a 2022-ben az egri Rátz László Vándorgyűlésen elhangzott szemináriumi foglalkozás alapján készült. A bemutatott feladatokkal felkelthetjük a középiskolás tanulók érdeklődését a gráfelméleti feladatok iránt. A cikkben közölt példák között amerikai, kínai, magyar versenyfeladatok mellett saját feladatok is szerepelnek. Ezekkel próbáltunk jól hasznosítható anyagot biztosítani a középiskolában tanító és a tehetséggondozásban résztvevő kollégáknak.
Fonyó Lajos – Fonyóné Németh Ildikó