Bevezető gondolatok
A magyarországi matematikának egyre dinamikusabban fejlődő területe a valószínűségszámítás. Ma már szebbnél szebb feladatok szerepelnek a példatárakban, felvételi vizsgákon és tanulmányi versenyeken. Ez a folyamat nemcsak hazánkra jellemző, hanem a matematikában jelenleg élenjáró ázsiai országokra és az Amerikai Egyesült Államokra is. Mivel a valószínűségszámítás a felsőoktatásban is fontos szerepet kap, ezért a világ legrangosabb egyetemei (Harvard, Stanford, Oxford, Cambridge) is nagy hangsúlyt helyeznek arra, hogy olyan jól képzett középiskolások kerüljenek be hozzájuk, akik a feltételek alapos figyelembevételével, a lehetőségek megfelelő csoportosításával, elemzésével, és megfelelő matematikai ismerettel következtetéseket tudnak levonni bizonyos események bekövetkezésének esélyére. Ezért az egyetemek legkiválóbb hallgatói, tanárai olyan matematikaversenyeket szerveznek középiskolásoknak, amelyeken a valószínűségszámítás domináns terület, és a feladatok igazi kihívást jelentenek a világ minden részéről érkező versenyzőknek.
Ebben a cikkben azt szeretnénk megmutatni, hogy az egyetemek által szervezett versenyeken, nemzetközi olimpiákon milyen típusú, illetve milyen nehézségi szintű feladatokat kell megoldani a középiskolás diákoknak. A feladatokat igyekeztük úgy kiválogatni, hogy azok kisebb csoportokban kapcsolódjanak egymáshoz, és mutassanak példát az adott területen belül egyszerűbb és bonyolultabb problémákra is. A cikk első részében elkalandozunk egy kicsit a koordináta-rendszerben, majd a kockán, illetve a poliédereken bolyongás világában.
A tárgyalt feladatok változatos módszerekkel oldhatók meg, a matematika számos területét érintik, és nehézségi szintjük is széles határok között mozog. Megoldásukhoz csak középiskolai ismeretek és jó ötletek szükségesek. A cikk megírásával egy jól hasznosítható anyagot szeretnénk adni a kollégáknak az iskolai szakköri munkához.
I. Bolyongás a koordináta-rendszerben
Az ebben a részben szereplő feladatokban koordináta-rendszeren a síkbeli koordináta-rendszert értjük.
1. feladat. A koordináta-rendszer \(K(1;2)\) pontjában tartózkodik Unka, a béka. Elkezd egy olyan mozgássorozatot, amely során véletlenszerűen ugrál valamelyik tengellyel párhuzamosan, egységnyi távolságokat haladva, a négy irányt egyenlő eséllyel választva. Mozgását akkor fejezi be, ha eléri az \(A(0;0)\), \(B(4;0)\), \(C(4;4)\) és \(D(0;4)\) csúcspontokkal rendelkező négyzet valamelyik oldalát.
Mennyi a valószínűsége annak, hogy a négyzet valamelyik függőleges oldalán fejezi be ugrássorozatát?
Megoldás. Elsőként szögezzük le, hogy annak a valószínűsége, hogy a béka nem éri el a négyzet egyik oldalát sem (vagyis hogy végtelen hosszú ugrássorozatba keveredik) 0, hiszen a \(k\)-adik lépés valószínűsége (bármelyik irányt is választja) \(\left(\frac{1}{4}\right)^k\), ami 0-hoz tart, ha \(k\) tart a végtelenhez.
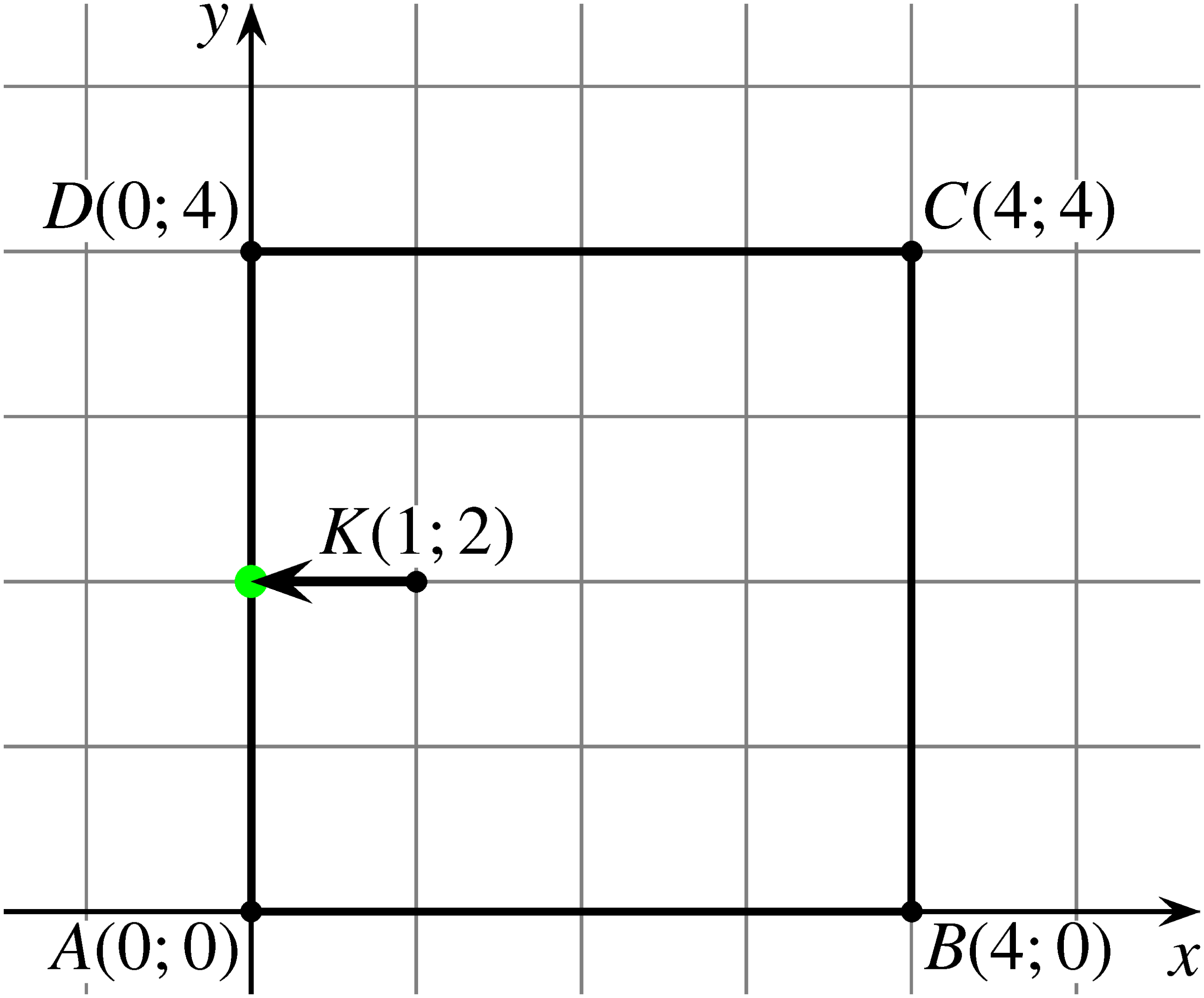
Ha a béka először balra ugrik, akkor azonnal eléri a négyzet függőleges \(DA\) oldalát, és mozgását befejezi. Ennek esélye: \[\displaystyle P_a=\frac{1}{4}.\]
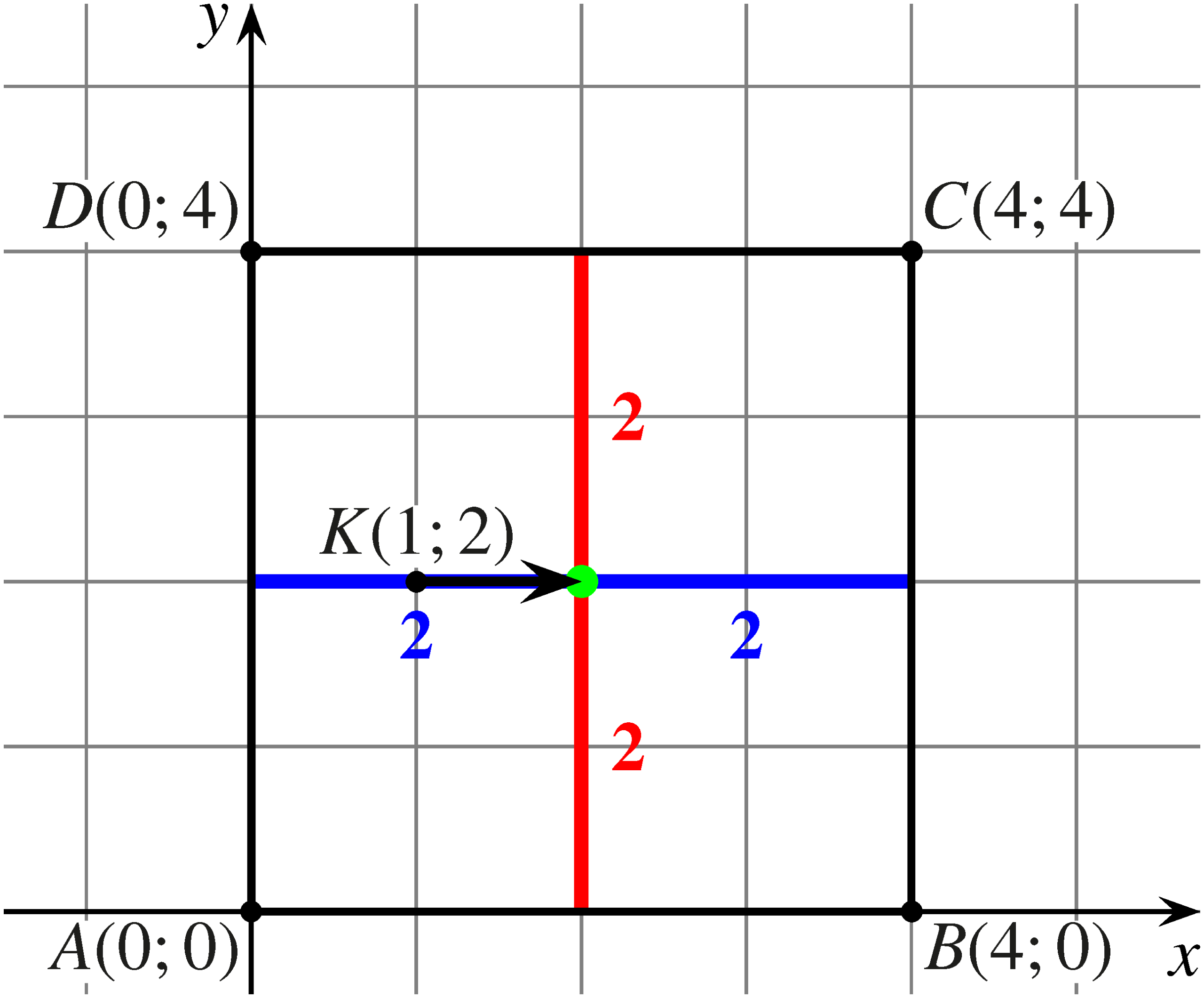
Ha a béka először jobbra ugrik, akkor a négyzet középpontjába jut, és innen (szimmetria okokból) mind a vízszintes, mind a függőleges oldalakat \(\frac{1}{2}\) valószínűséggel éri el. Így ebben az esetben a keresett valószínűség: \[\displaystyle P_b=\frac{1}{4}\cdot \frac{1}{2}=\frac{1}{8}.\]
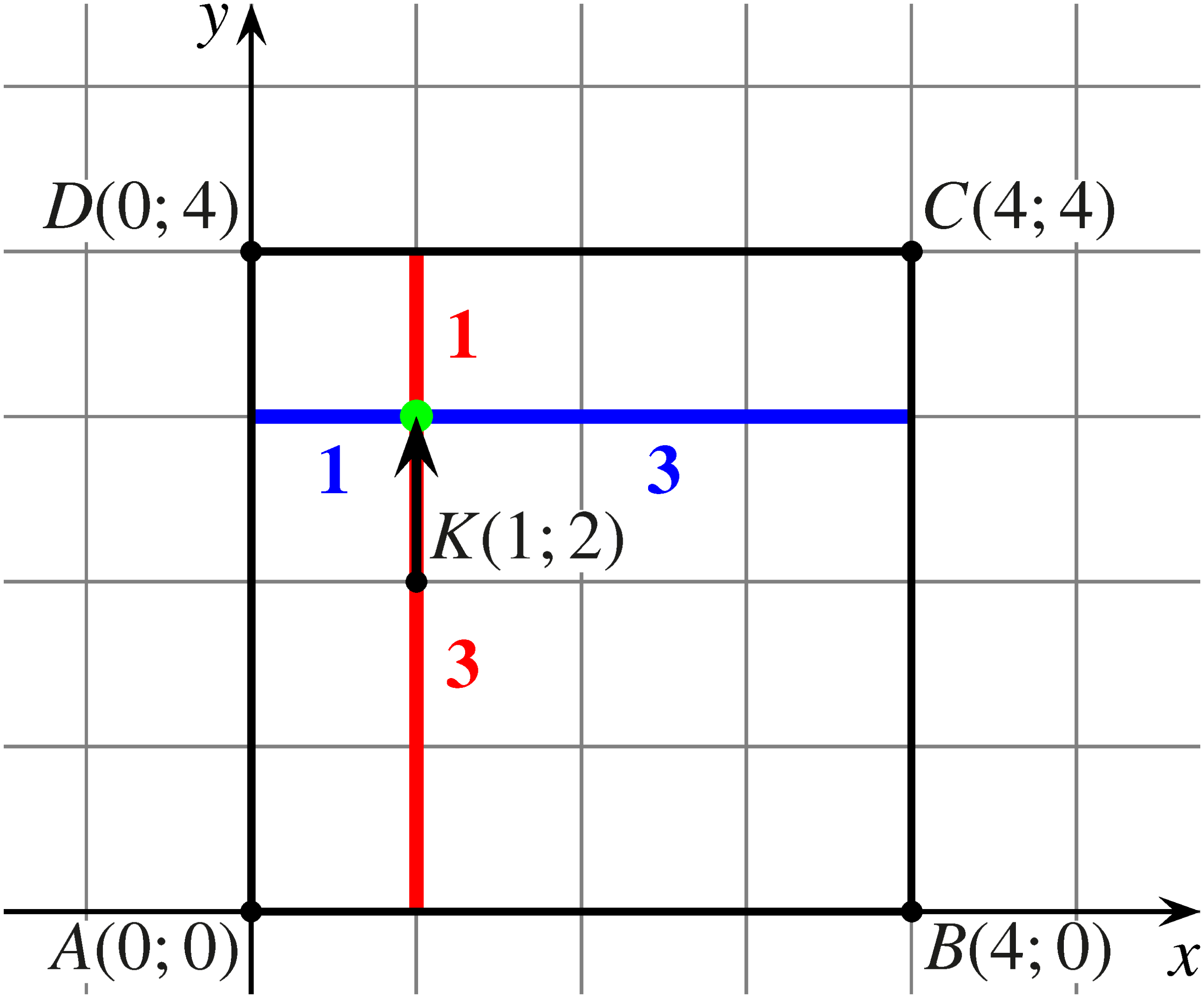
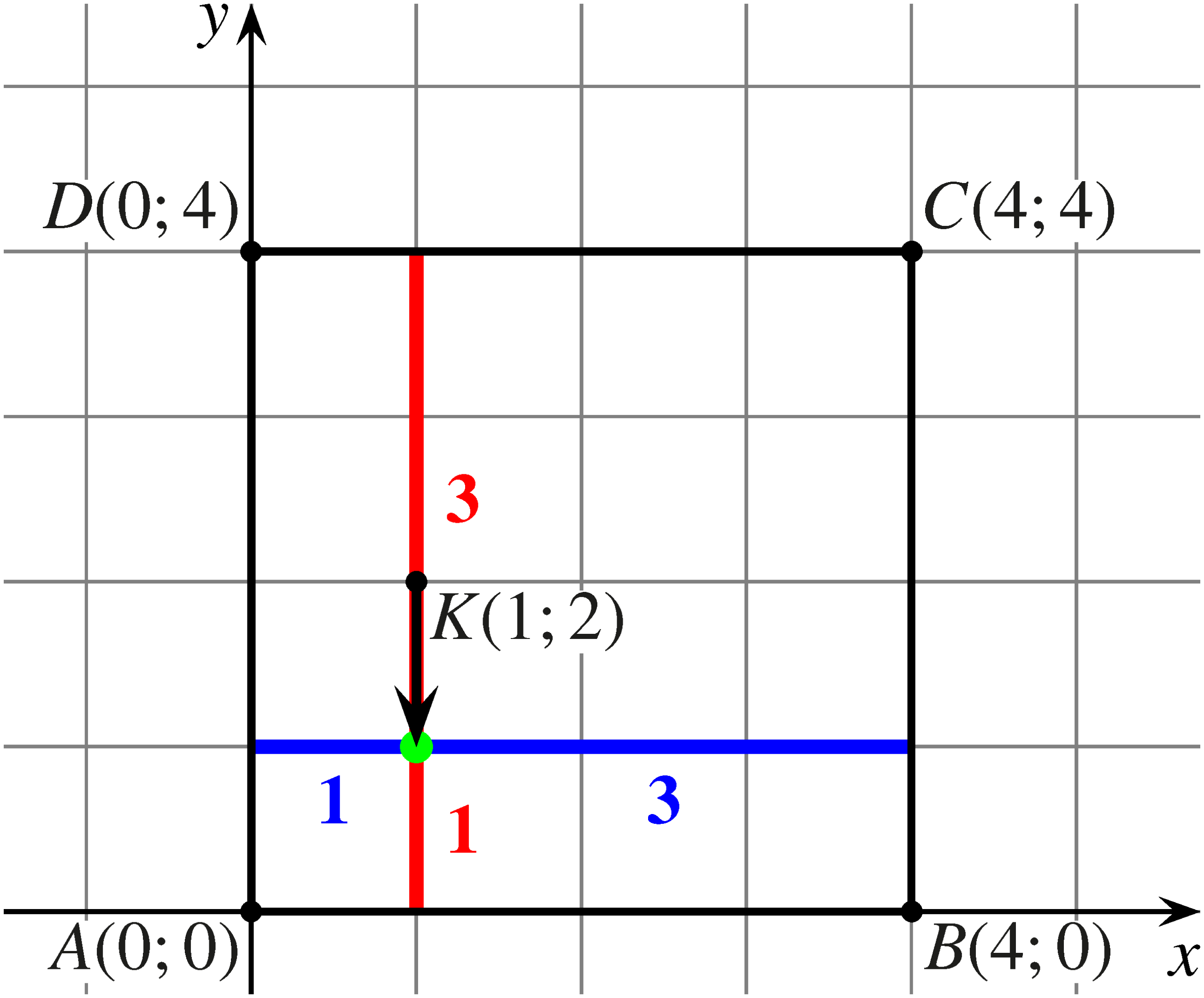
Ha a béka először felfelé vagy lefelé ugrik, akkor két vízszintes-függőleges oldalpártól szimmetrikus helyzetbe jut, és ezután egyenlő eséllyel fejezi be a mozgását a vízszintes, illetve a függőleges oldalon. Így ebben az esetben a keresett valószínűség: \[\displaystyle P_{bc}=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}.\] Az eseteket összesítve: \[\displaystyle P=\frac{1}{4}+\frac{1}{8}+\frac{1}{4}=\frac{5}{8}.\]
2. feladat. Egy részecskét a síkbeli derékszögű koordináta-rendszerben a \(K(0;0)\) ponttól a \(V(n;n)\) ( \(n\in {\mathbb{N}}^+\)) pontig mozgatjuk.
Haladását egy szabályos pénzérme segítségével irányítjuk, az alábbiak szerint:
1. A \(P(x;y)\), \(x\), \(y\in \mathbb{N}\), \(x\), \(y<n\) pontból írás dobása esetén a \(Q(x+1;y)\), fej dobása esetén pedig az \(R(x;y+1)\) pontba lép.
2. A \(P(n;y)\), \(y<n\) pontból írás dobása esetén nem mozdul el, fej dobása esetén pedig az \(R(n;y+1)\) pontba lép.
3. A \(P(x;n)\), \(x<n\) pontból írás dobása esetén a \(Q(x+1;n)\) pontba lép, fej dobása esetén pedig nem mozdul el.
Mennyi a valószínűsége annak, hogy a részecske pontosan \(2n+k\) ( \(k\in \mathbb{N}\)) dobás után érkezik meg a \(V(n;n)\) pontba?
Megoldás. A részecske a szabályok alapján a \((0;0)\), \((n;0)\), \((n;n)\), \((0;n)\) csúcspontokkal rendelkező négyzeten belül maradva írásra „jobbra”, fejre „felfelé” mozdul 1-et – ha ez lehetséges.
a) Vizsgáljunk meg egy konkrét esetet, és az ebből nyerhető törvényszerűségeket használjuk fel az általános eset megoldásához. Például \(n=3\), \(k=4\) esetén felírva a legalább 3-3 írást és fejet tartalmazó \(2n+k=10\) hosszúságú dobássorozatokat, és a részecske mozgását a koordináta-rendszerben követve, látható, hogy az IFFFIFFFFI, IFFFFIFFFI, IFFFFFIFFI, IFFFFFFIFI, IFFFFFFFII (fej-írás) dobássorozatok ugyanazt az útvonalat jelölik ki a részecske számára.
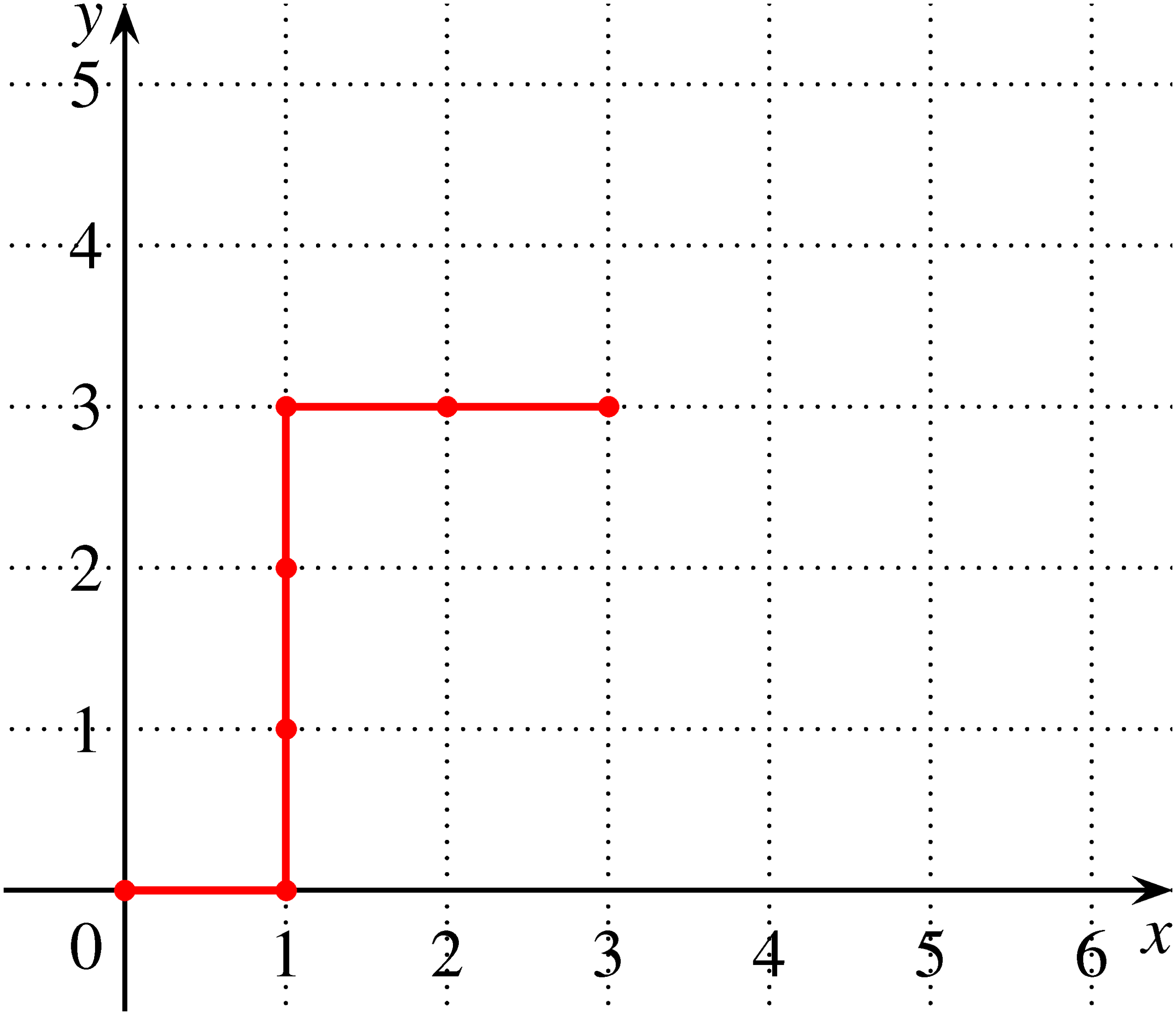
A közölt példából látható, hogy nincs kölcsönösen egyértelmű kapcsolat a tényleges mozgás és a dobások jelsorozata között. Azért, hogy ezt a problémát feloldjuk, engedjük meg, hogy a részecske folytathassa útját jobbra, illetve felfelé akkor is, ha az első vagy a második koordinátája eléri vagy meghaladja \(n\) értékét, és vizsgáljuk együtt a tényleges és az általunk elképzelt kibővített mozgást. A továbbiakban piros, illetve kék szakasszal jelöljük a részecske által valóban megtett, illetve gondolatban végigjárt útszakaszokat.
b) \(n=3\), \(k=4\) esetén (amikor a várt lépésszám \(2n+k=10\)) a 4 fejből és 6 írásból álló IIFIIIFFIF dobássorozat esetén vizsgálva a részecske valódi és kibővített mozgását, láthatjuk, hogy a részecske a várt 10-es lépésszámnál hamarabb, már a 8. dobás után eléri a \(V(3;3)\) pontot.
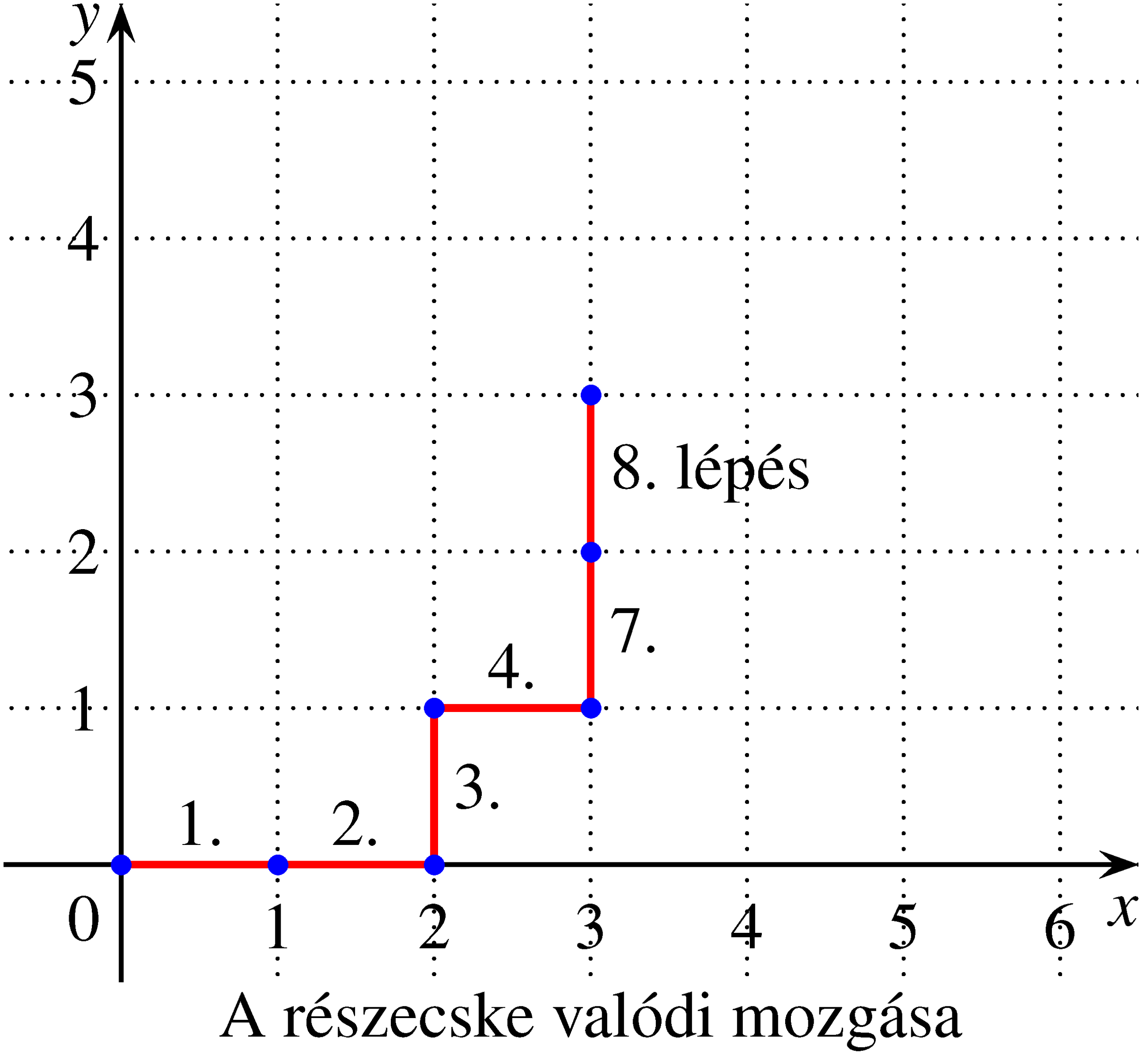
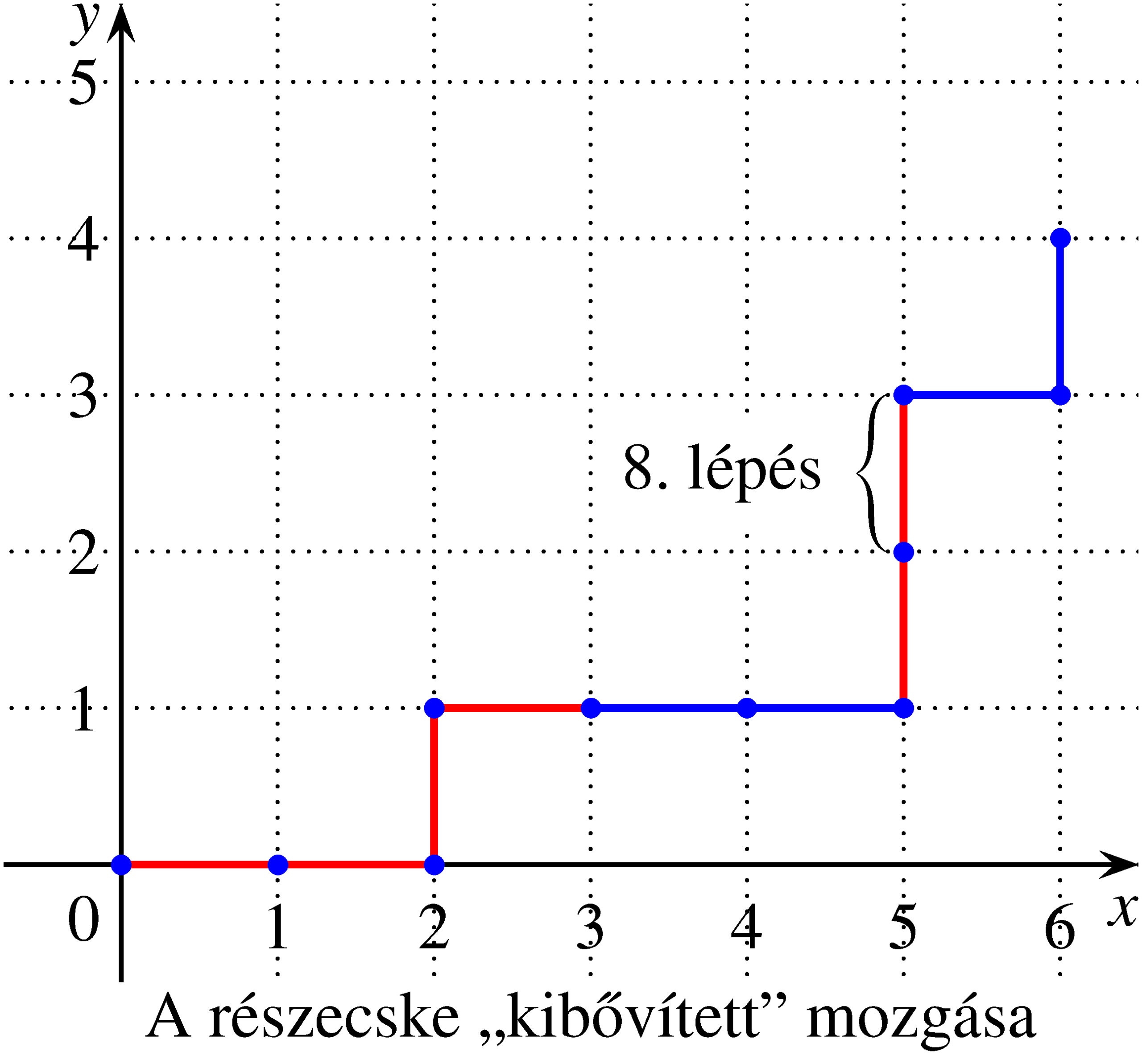
Az ábrák alapján látható, hogy a részecske a várt lépésszámnál hamarabb ér célba. Ez nyilván azért alakult így, mert 3-nál több fej és 3-nál több írás szerepelt a dobások között, miközben az utolsó fej előtt szerepelt már három írás, és az utolsó írás előtt szerepelt már három fej. Ebből arra következtethetünk, hogy a mozgás során a részecskének az egyik irányba pontosan \(n+k\), a másik irányba \(n\) lépést kell megtennie. Így a „kibővített” mozgás során a részecskének az \(E_1(n+k;n)\), vagy \(E_2(n;n+k)\) pontok valamelyikébe kell eljutnia.
Emellett arra is figyelni kell, hogy megfelelő arányú I, F dobások esetén a kibővített mozgás során a részecske ne a \(T_1(n+k-1;n)\), illetve a \(T_2(n;n+k-1)\) pontokból jusson el \(E_1\), \(E_2\) pontokba, hanem az utolsó dobás az \(n\)-edik fej, vagy az \(n\)-edik írás legyen. (Ez a feltétel biztosítja azt, hogy a részecske a \((2n+k)\)-adik lépését is biztosan végre fogja hajtani.) Ilyen dobássorozat lehet pl. az FFIFFIFFFI. Ekkor a részecske mozgása:
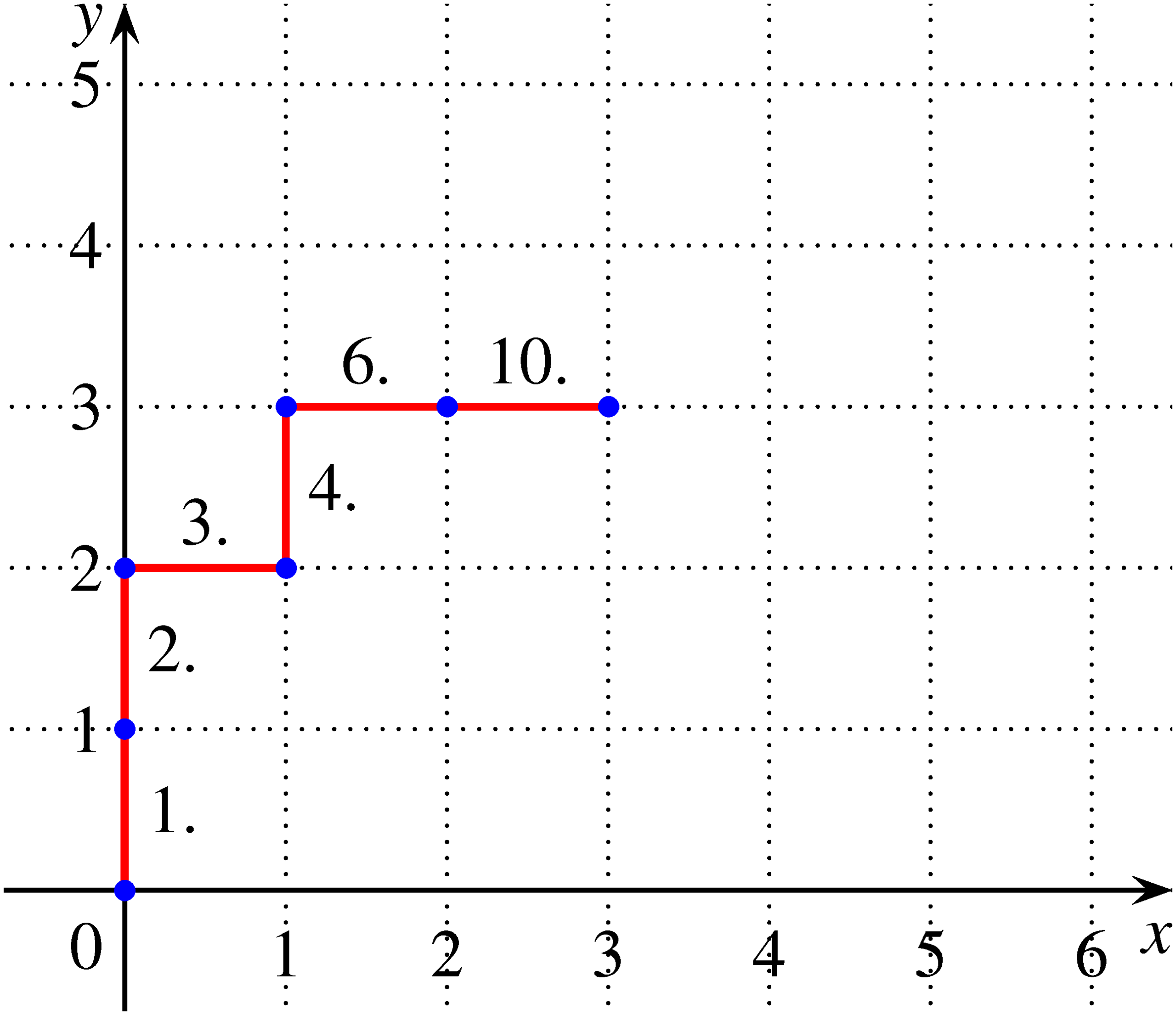
Tehát a vizsgált konkrét példák alapján a részecske utolsó lépése csak a
\(D_1(n+k;n-1)\) \(\to\) \(E_1(n+k;n)\) vagy
\(D_2(n-1;n+k)\) \(\to\) \(E_2(n;n+k)\) lehet.
Ez alapján az első \(2n+k-1\) dobáson belül az írás-fej megoszlás valamilyen sorrend szerint \((n-1):(n+k)\), az utolsó dobás meghatározott. Mivel bármely dobásnál a fej és az írás dobásának az esélye is \(\frac{1}{2}\), ezért a keresett valószínűség: \[\displaystyle P_k=2\binom{2n+k-1}{n-1}\left(\frac{1}{2}\right)^{2n+k}=\binom{2n+k-1}{n-1}\left(\frac{1}{2}\right)^{2n+k-1}.\]
3. feladat. Ugri, a szöcske, a koordináta-rendszerben mozog. A \(K(0;0)\) pontból indul, másodpercenként egy egységet halad, és rácspontról rácspontra ugrik. A haladási irányokat véletlenszerűen, azonos valószínűséggel választja ki. Mozgását addig folytatja, amíg olyan \(P\) pontba nem ér, amelyet egy másik útvonalon gyorsabban is elérhetett volna vagy akár el is ért.
Például, ha a \((0;0)\to(1;0)\to(1;1)\to(1;2)\to(0;2)\) útvonalon halad, akkor a \(P(0;2)\) pontban megáll, mivel oda a \((0;0)\to(0;1)\to(0;2)\) úton 2 másodperc alatt is el tudott volna jutni.
Mennyi Ugri ugrásai számának várható értéke?
Megoldás. Jelöljük a szöcske mozgásirányait az ábra szerint.
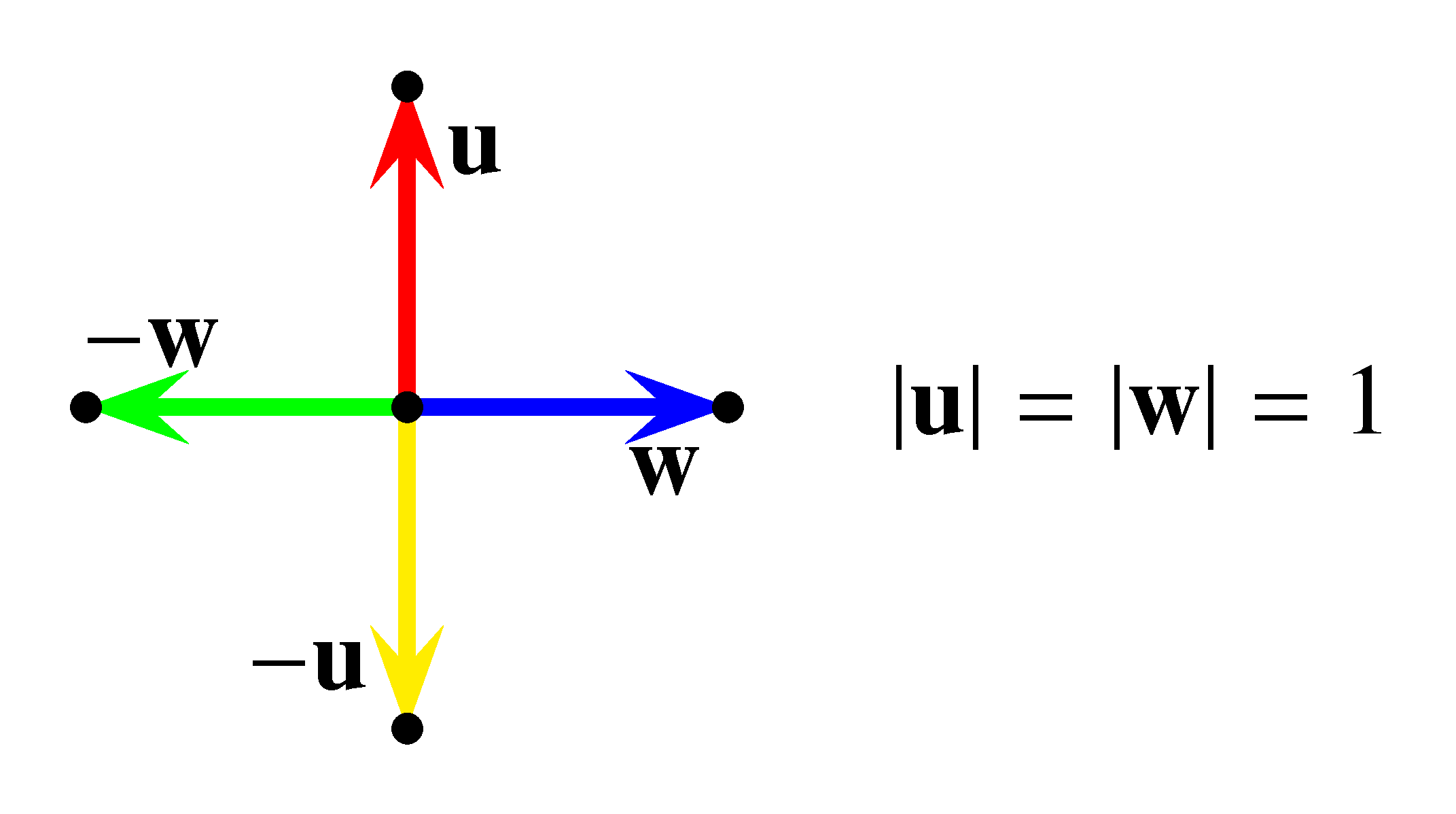
Ekkor Ugri az első ugrását mindenképpen végre tudja hajtani, és az általánosság megszorítása nélkül feltehetjük, hogy az \(\mathbf{u}\) irányú.
Jelölje a szöcske további lépései számának várható értékét \(e_1\). Ugri mozgását tovább vizsgálva a második lépését is mindenképpen végre tudja hajtani, és háromféleképpen mozoghat.
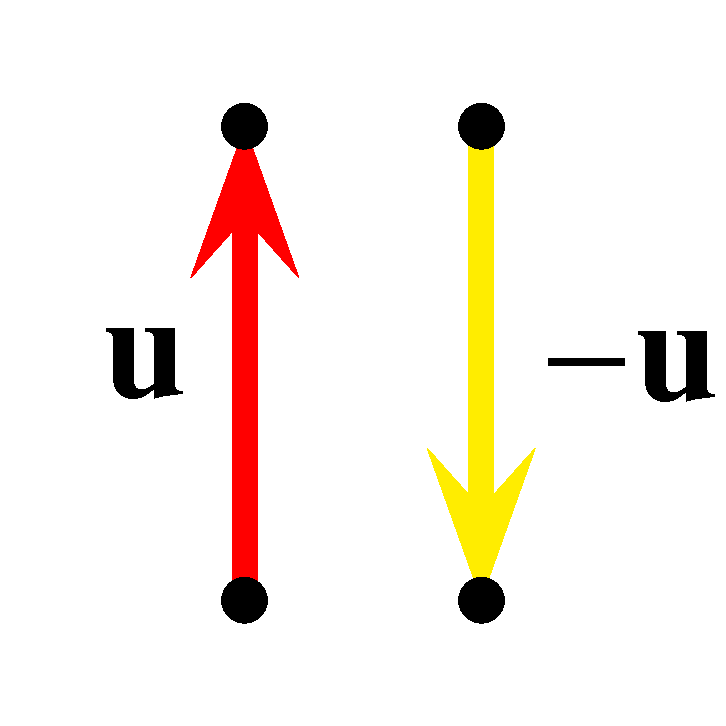
\(\frac{1}{4}\) valószínűséggel \(-\mathbf{u}\) irányba halad, és ekkor útja véget ér.
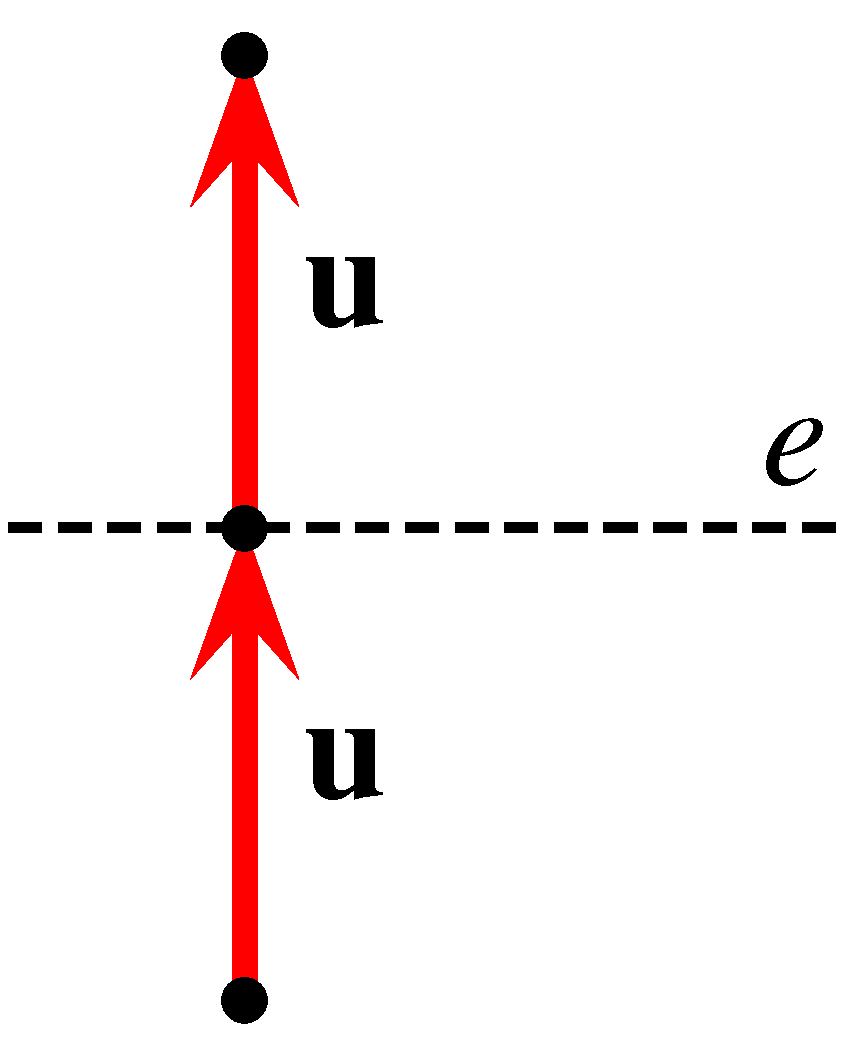
\(\frac{1}{4}\) valószínűséggel \(\mathbf{u}\) irányba halad, és ezután várhatóan még \(e_1\) lépést tesz meg, hiszen ezután pontosan akkor akad el, ha \(-\mathbf{u}\) irányt választ, tehát feltételezhető, hogy \(e_1+1\) a várható lépések száma.
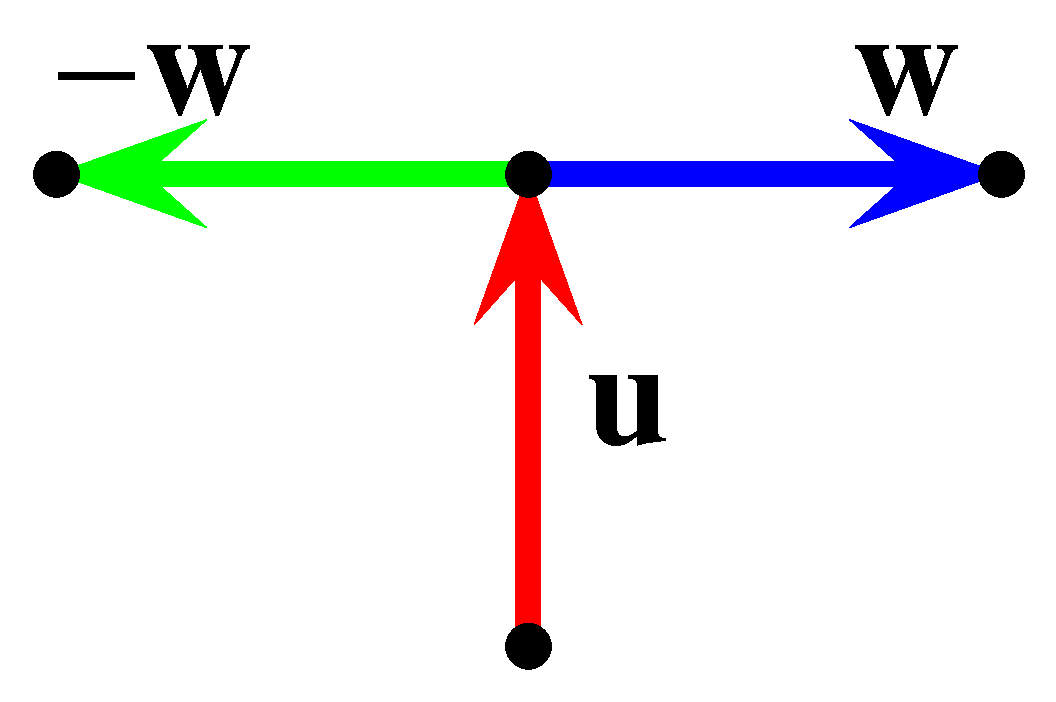
\(\frac{1}{2}\) valószínűséggel \(\mathbf{u}\)-ra merőleges irány szerint halad, és ezután várhatóan még \(e_2\) (egyelőre ismeretlen számú) lépést tesz meg.
Az a), b), c) esetek figyelembevételével: \[\displaystyle e_1=\frac{1}{4}\cdot 1+\frac{1}{4}\cdot (e_1+1)+\frac{1}{2}\cdot (e_2+1).\]
Határozzuk most meg \(e_2\) értékét. Azaz feltételezzük, hogy \(\mathbf{u}\) után Ugri egy erre merőleges irányt (például \(\mathbf{w}\)) választott \(\frac{1}{2}\) valószínűséggel.
d) A c) eset szerinti haladás esetén Ugri biztosan folytathatja útját.
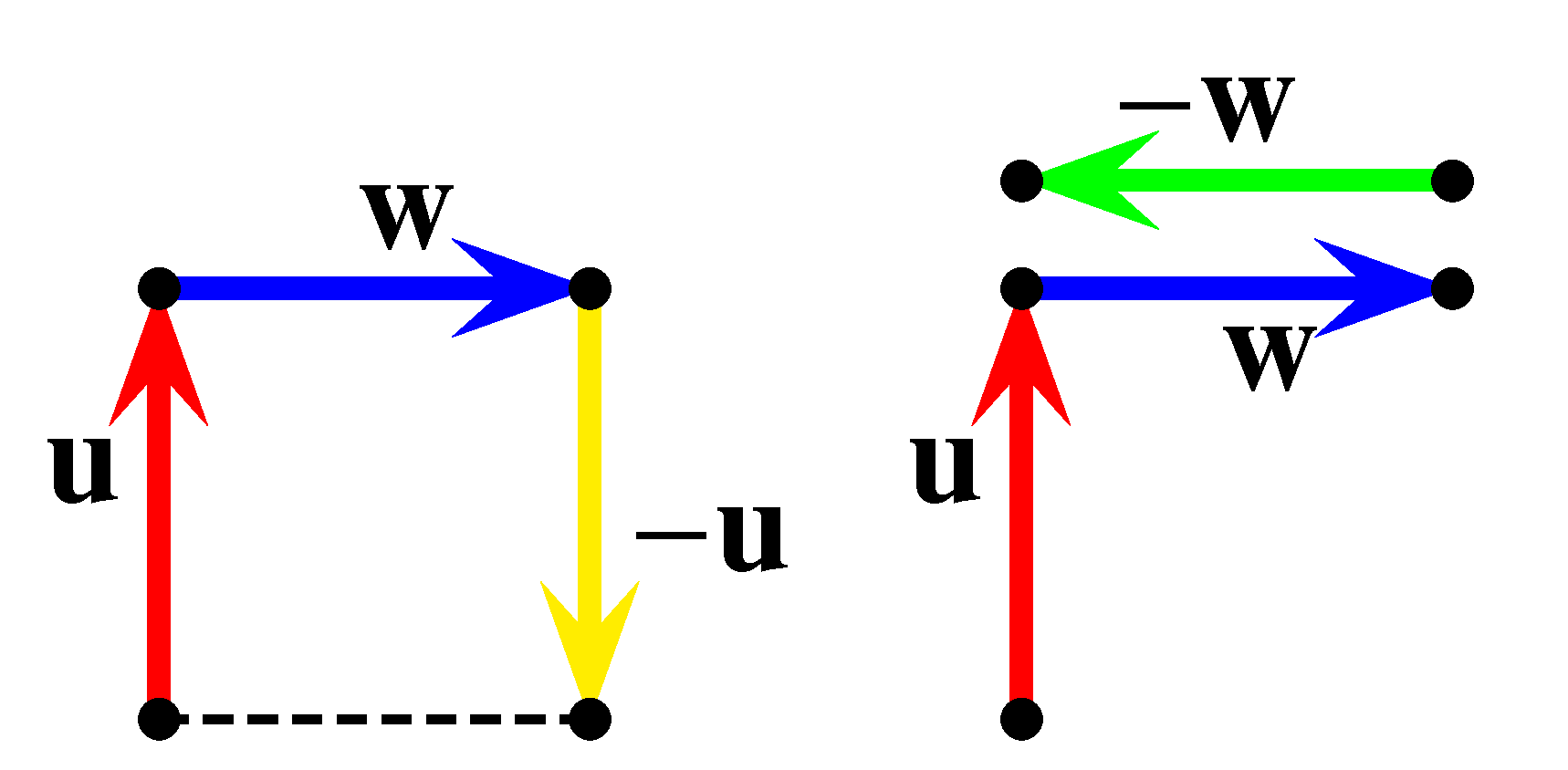
\(\frac{1}{2}\) valószínűséggel tesz egy lépést \(-\mathbf{u}\) vagy \(-\mathbf{w}\) irányba, és ekkor útja véget ér.
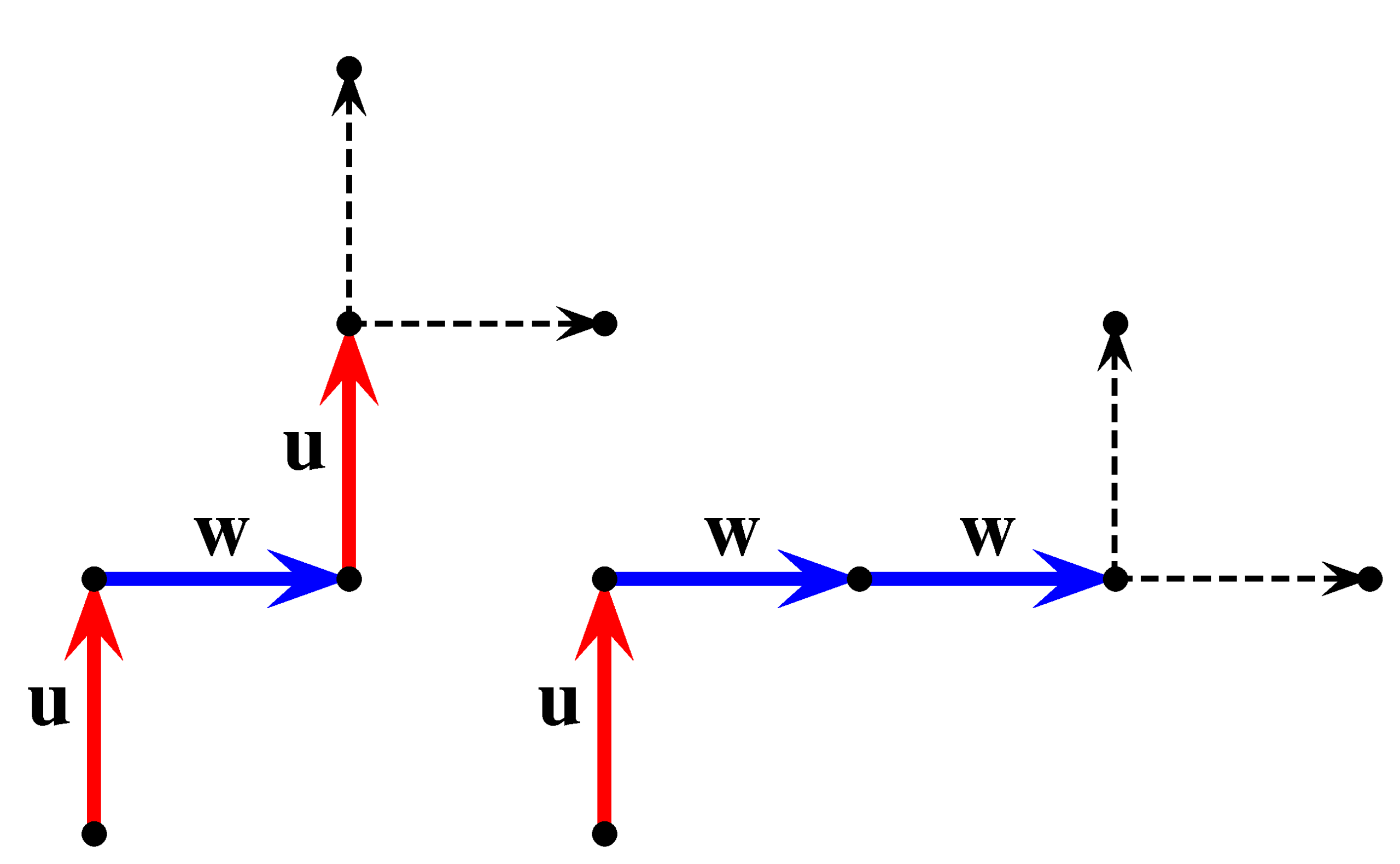
\(\frac{1}{2}\) valószínűséggel tesz egy lépést \(\mathbf{u}\) vagy \(\mathbf{w}\) irányba, és ezután várhatóan még \(e_2\) lépést tesz meg, hiszen ezután is pontosan akkor akad el, ha a \(-\mathbf{w}\) vagy a \(-\mathbf{u}\) irányt választja. Ebben az esetben a lépések várható értéke \(e_2+1\).
A d) és e) esetek figyelembevételével: \[\displaystyle e_2=\frac{1}{2}\cdot 1+\frac{1}{2}\cdot (e_2+1).\]
Innen \(e_2=2\), ezért \(e_1=\frac{8}{3}\). Emlékeztetünk, hogy \(e_1\) az első lépést követő lépések számának várható értéke volt, így Ugri várható ugrásainak száma \(e_1+1=\frac{11}{3}\).
II. Bolyongás kockán
4. feladat. Z, a hangya egy kocka csúcsai között vándorol. Minden percben elhagyja azt a csúcsot, ahol addig tartózkodott, és egy élen haladva átvándorol egy szomszédos csúcsba.
Mennyi a valószínűsége annak, hogy 4 perc múlva visszatér oda, ahonnan elindult, ha minden lépésben egyenlő eséllyel választja meg a haladási irányt?
Megoldás.
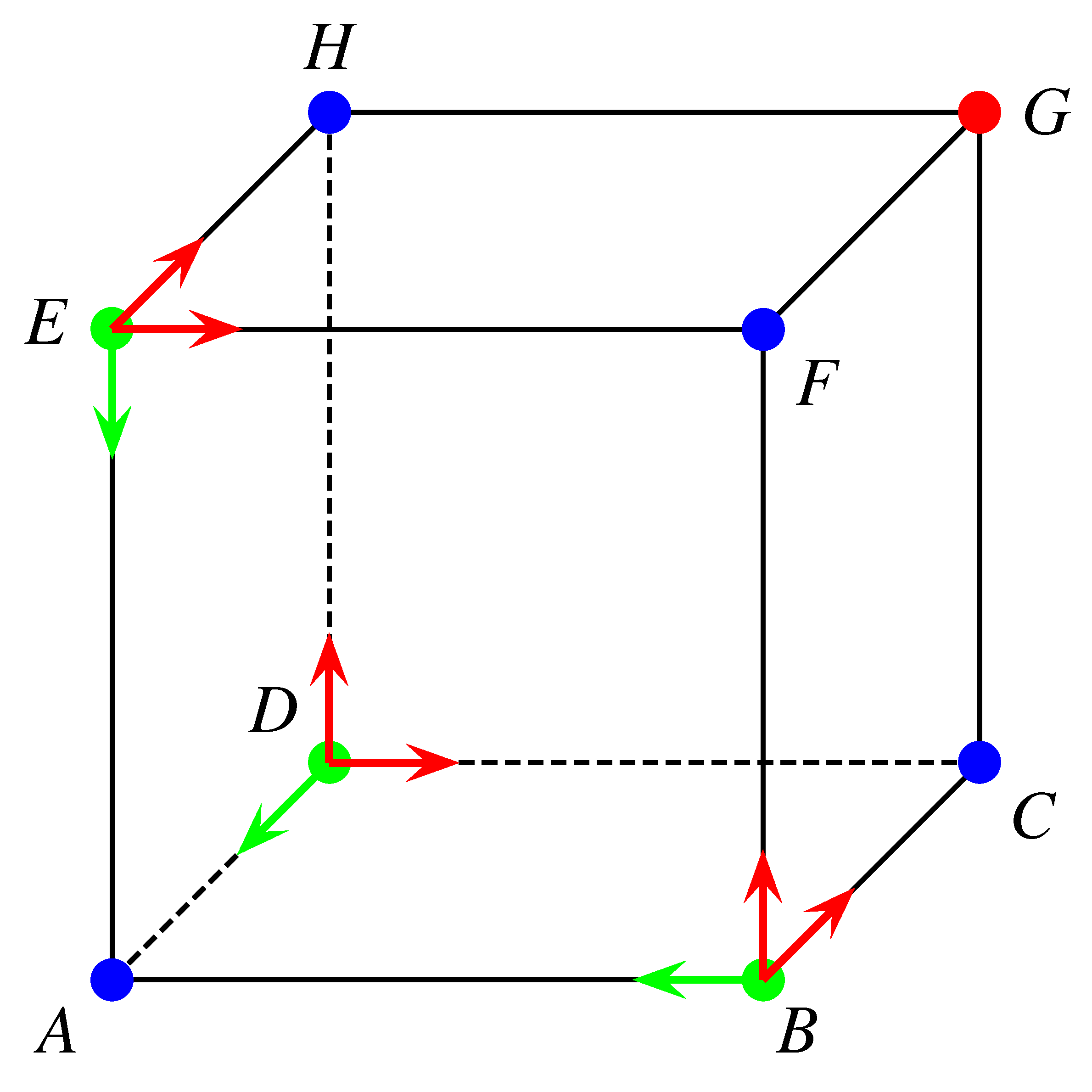
Az általánosság megszorítása nélkül feltehetjük, hogy Z az \(A\) csúcsból indul.
A hangya a páros percek végén az \(A\), \(C\), \(F\), \(H\), míg a páratlan percek végén a \(B\), \(D\), \(E\), \(G\) csúcsokban tartózkodik. Ha a harmadik perc végén Z a \(G\) pontban van, akkor a negyedik perc végére nem tud visszajutni \(A\)-ba.
Vizsgáljuk meg, hogy mekkora valószínűséggel jut három perc alatt Z a \(G\) csúcsba. A lehetséges útvonalak az alábbiak közül kerülhetnek ki: \(ABCG\), \(ABFG\), \(ADCG\), \(ADHG\), \(AEFG\), \(AEHG\).
Mivel a hangya minden lépését 3 irány szerint választhatja ki, ezért a \(G\)-be jutásának esélye: \[\displaystyle P(G)=6\cdot \left(\frac{1}{3}\right)^3=\frac{2}{9},\] és így a \(B\), \(D\), \(E\) csúcsokba érkezésének valószínűsége: \[\displaystyle P(B,D,E)=1-P(G)=\frac{7}{9}.\]
Az ábra szerint a \(B\), \(D\), \(E\) pontokból a 4. percben \(\frac{1}{3}\) eséllyel tér vissza a hangya \(A\)-ba, ezért a keresett valószínűség: \[\displaystyle P=\frac{7}{9}\cdot \frac{1}{3}=\frac{7}{27}.\]
5. feladat. Z, a hangya egy kocka csúcsai között vándorol. Minden percben elhagyja azt a csúcsot, ahol addig tartózkodott, és egy élen haladva átvándorol egy szomszédos csúcsba.
Mennyi a valószínűsége annak, hogy \(2k\) ( \(k\in {\mathbb{N}}^+\)) perc múlva visszatér oda, ahonnan elindult, ha minden lépésben egyenlő eséllyel választja meg a haladási irányt?
Megoldás.
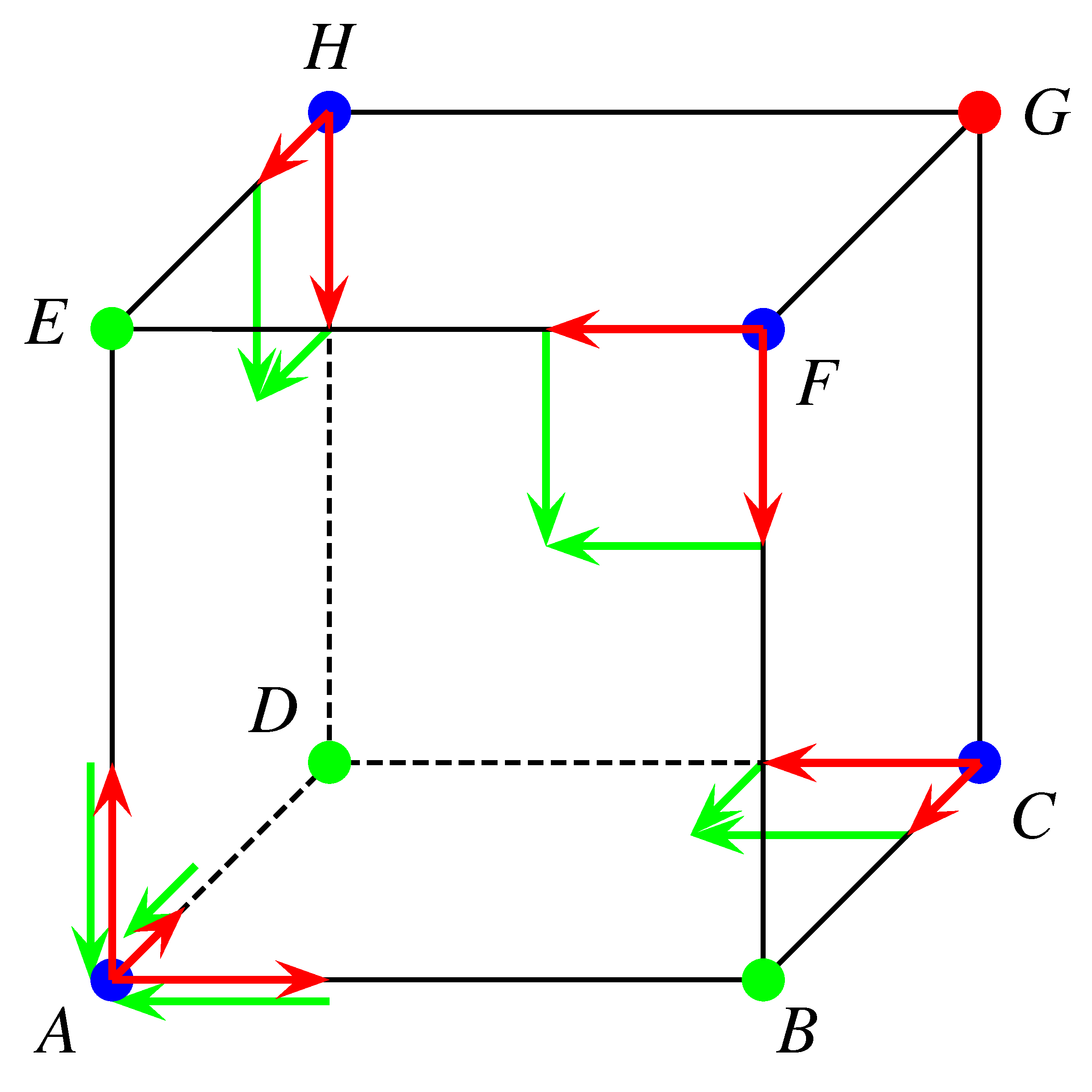
Az általánosság megszorítása nélkül feltehetjük, hogy Z az \(A\) csúcsból indul.
Jelölje \(p_k\) annak a valószínűségét, hogy Z a \((2k)\)-adik perc végén ismét \(A\)-ban van. Használjuk fel, hogy Z a páros percek végén csak az \(A\), \(C\), \(F\) és \(H\) csúcsok valamelyikén tartózkodhat.
A hangya a \((2k)\)-adik perc végére csak az alábbi két lényegileg különböző módon jutahat vissza \(A\)-ba. Vagy \(A\)-ból elindul tetszőlegesen \(B\)-be, \(D\)-be vagy \(E\)-be, majd utána visszatér \(A\)-ba, vagy az ábra szerint a \(C\), \(F\), \(H\) csúcsokból először a két piros nyíl egyikének irányába mozdul el, majd utána az egyik zöld irány szerint érkezik meg \(A\)-ba.
Figyelembe véve, hogy a hangya minden lépését háromféle irányba teheti meg, \[\displaystyle p_{k+1}=p_k\cdot 1\cdot \frac{1}{3}+(1-p_k)\cdot \frac{2}{3}\cdot \frac{1}{3}=\frac{1}{9}p_k+\frac{2}{9}.\] A \[\displaystyle \lim\limits_{k\to \infty}p_{k+1}=\lim\limits_{k\to \infty}p_k=x\] egyenlőség alapján: \[\displaystyle x=\frac{1}{9}x+\frac{2}{9}\] \[\displaystyle x=\frac{1}{4}\] \[\displaystyle p_{k+1}-\frac{1}{4}=\frac{1}{9}\left(p_k-\frac{1}{4}\right).\]
A kapott egyenlőség alapján a \(\biggl(p_k-\frac{1}{4}\biggr)\) sorozat olyan mértani sorozat, amelynek nulladik tagja és hányadosa \[\displaystyle p_0-\frac{1}{4}=1-\frac{1}{4}=\frac{3}{4},\] illetve \[\displaystyle q=\frac{1}{9}.\]
Ennek figyelembe vételével: \[\displaystyle p_k-\frac{1}{4}=\frac{3}{4}\cdot \left(\frac{1}{9}\right)^k,\] \[\displaystyle p_k=\frac{1}{4}+\frac{3}{4}\cdot \left(\frac{1}{9}\right)^k.\]
6. feladat. Egyik nap Z meghívta 7 társát vendégségbe. A 8 hangya egy kocka 8 csúcsában telepedett le. Egy adott pillanatban mindegyikük elindult egy kiválasztott élen, és átmászott egy szomszédos csúcsba.
Mennyi a valószínűsége annak, hogy egyik hangya sem találkozott útközben vagy az út végén valamelyik társával, ha minden lépésben egymástól függetlenül, egyenlő eséllyel választják meg a haladási irányt?
Megoldás. a) A hangyák két 4 hosszúságú körön mozognak (az ábra szerint a kocka egy-egy lapján járnak körbe).
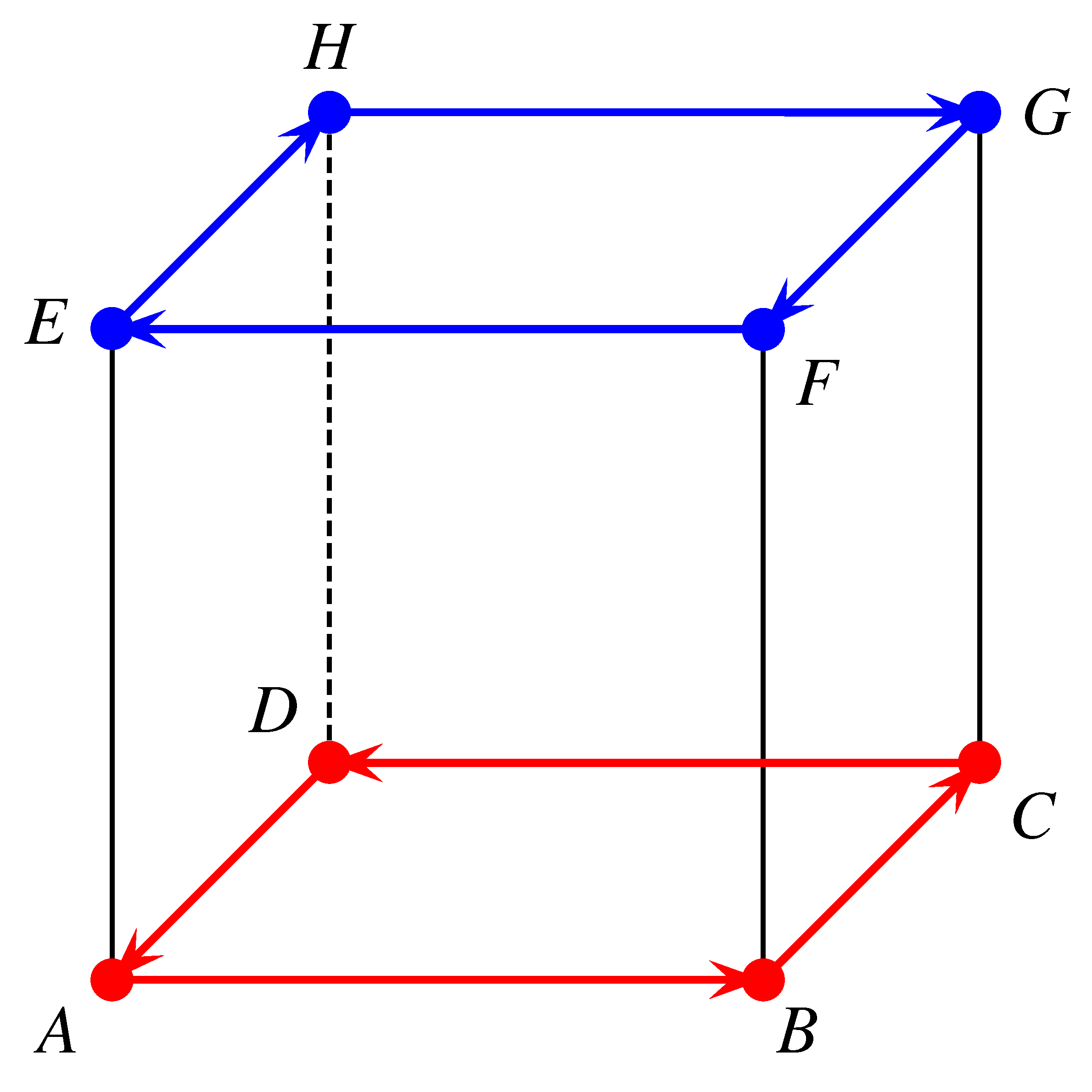
Ebben az esetben a hangyák mozgása a kocka két szemközti lapján történik, amelyek kiválasztása háromféleképpen történhet. Mivel a körökön belül a vándorlás forgásiránya két-kétféleképpen jelölhető ki, ezért a kedvező esetek száma \(3\cdot 2^2=12\).
b) A hangyák egy 8 hosszúságú körön mozognak (lásd az ábrán).
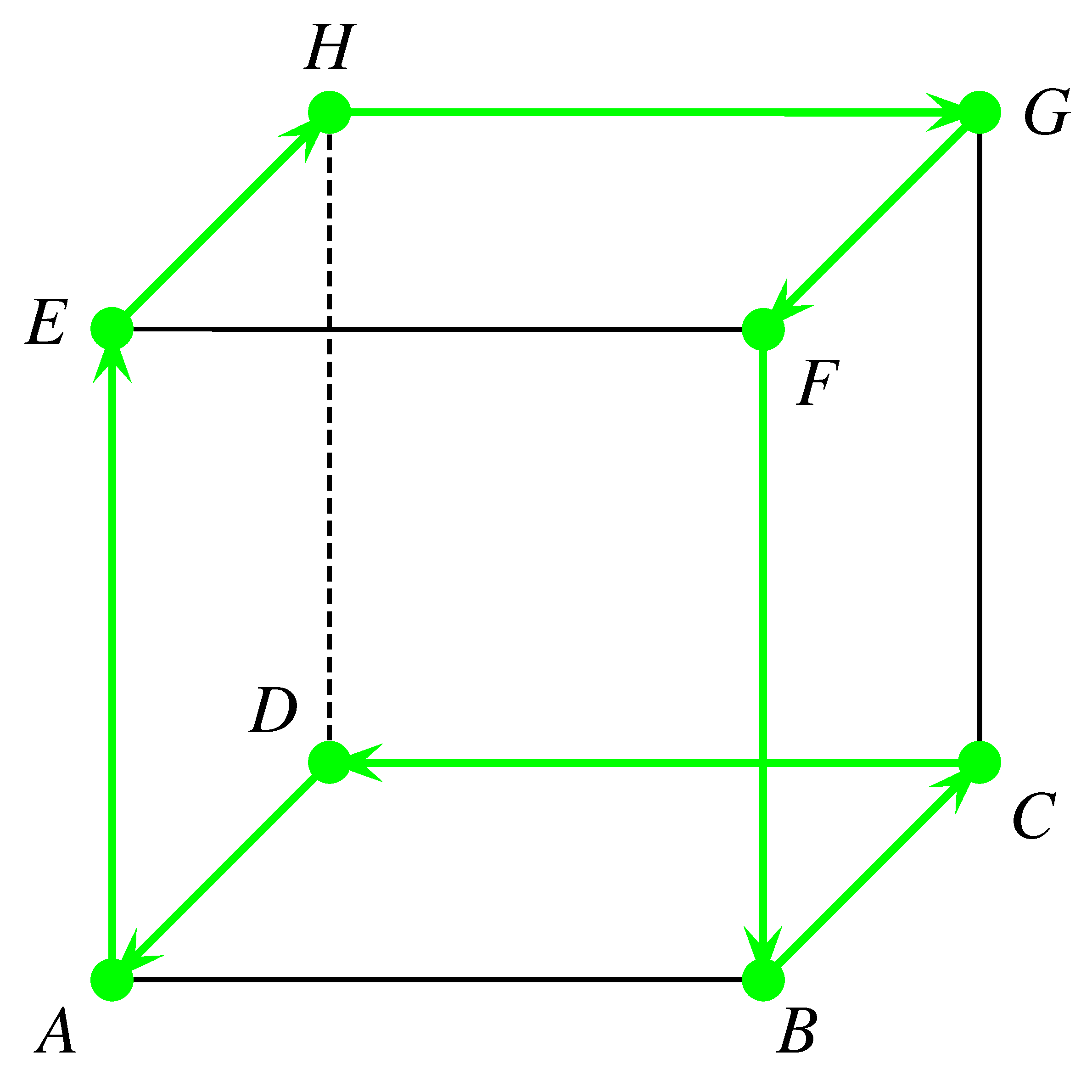
Ebben az esetben a vándorlás során a kocka két szemközti lapján a hangyák csak 2 él mentén mozognak, ezek kiválasztása háromféleképpen történhet. A két kiválasztott lap egyikén a hangyák vízszintesen, a másikon függőlegesen vándorolnak. A vízszintes és függőleges irányok lapokhoz rendelése kétféleképpen történhet.
Végül a 8-as körön belül a vándorlás forgásiránya kétféle lehet, így a kedvező esetek száma ebben az esetben \(3\cdot 2\cdot 2=12\).
Mivel a hangyák mindegyike a mozgását háromféle irány szerint választhatja meg, ezért a keresett valószínűség \[\displaystyle P=\frac{12+12}{3^8}=\frac{8}{2187}.\]
III. Bolyongás poliéderen
7. feladat. Amíg Z egy kockán bandukol, addig Atom Anti egy oktaéder élein vándorol, és ő is percenként megy át egy adott csúcsból egy szomszédosba, egyenlő valószínűséggel választva a lehetőségek közül.
Mennyi a valószínűsége annak, hogy indulása után 5 perccel a kezdőponttal szomszédos csúcsban tartózkodik?
Megoldás.
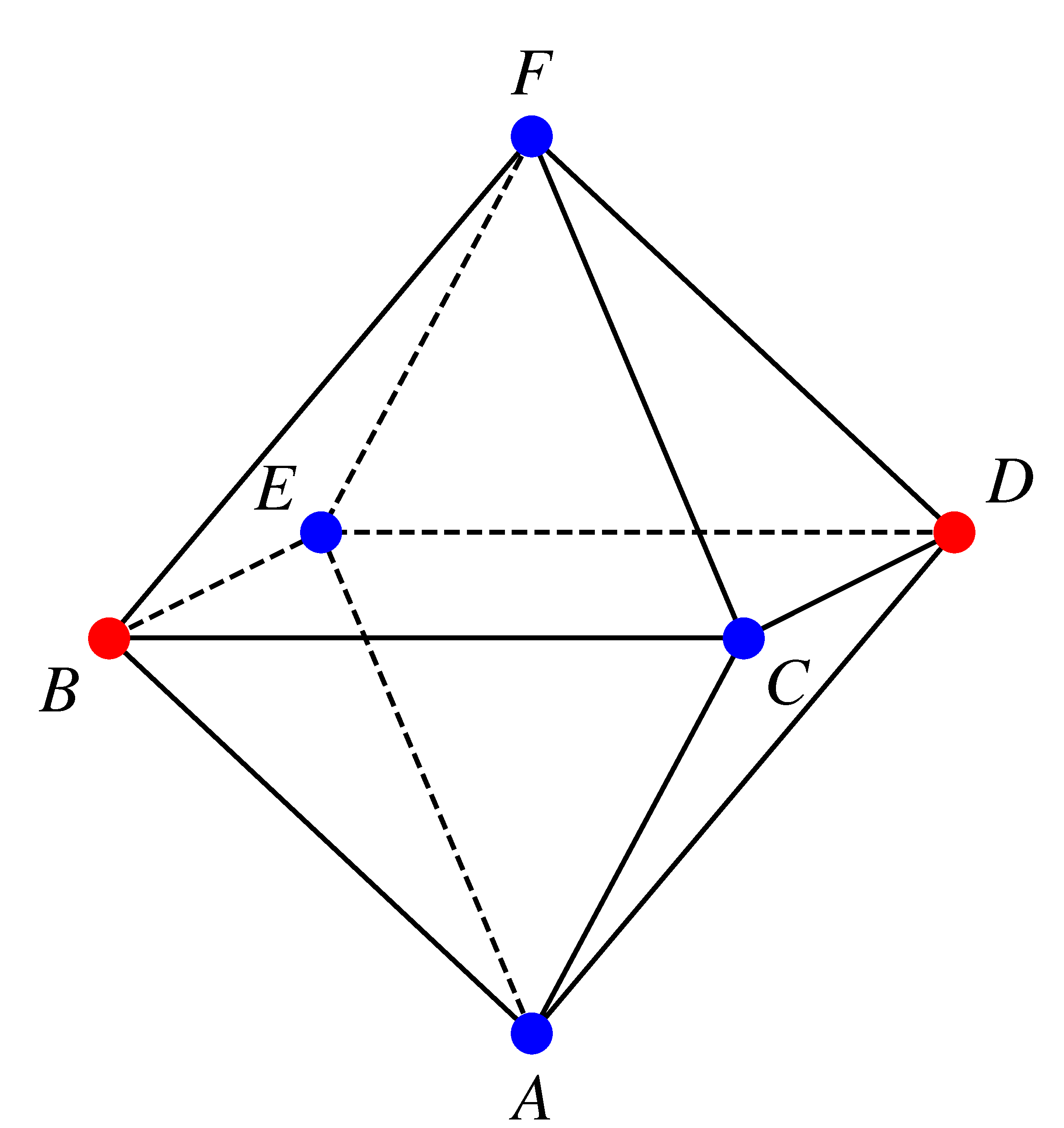
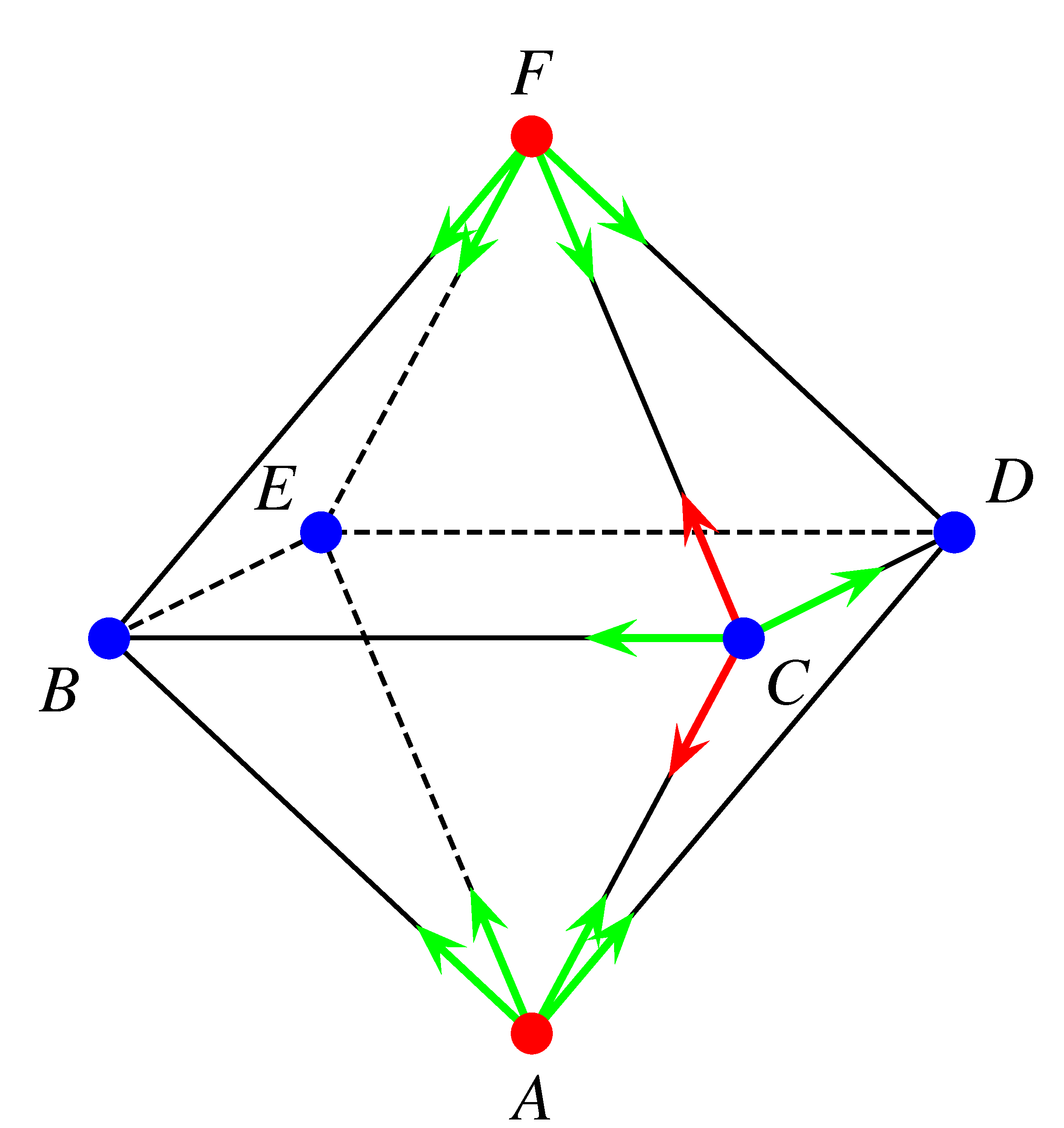
Az ábrákból látható, hogy az oktaéderben bármely csúccsal négy másik csúcs szomszédos és egy átellenes. Ezért az általánosság kedvéért feltehetjük, hogy Anti az \(A\) csúcsból indul.
Jelölje \(p_k\) annak esélyét, hogy Anti a \(k\)-adik perc végén egy \(A\)-val szomszédos csúcsban van ( \(k\in \mathbb{N}\)). Ekkor \(p_0=0\), \(p_1=1\). Rekurzív gondolatmenetet alkalmazva: ha a \(k\)-adik perc végén a hangya \(p_k\) valószínűséggel a \(B\), \(C\), \(D\), \(E\) pontokban áll, akkor a négy haladási irányból kettővel \(A\)-val szomszédos helyeken marad, míg ha \({1-p}_k\) valószínűséggel az \(A\) vagy \(F\) pontokban tartózkodik, akkor a következő lépésével biztosan \(A\)-val szomszédos csúcsba jut. Így \[\displaystyle p_{k+1}=\frac{1}{2}{\cdot p}_k+1\cdot (1-p_k)=1-\frac{1}{2}p_k.\] A kapott képlet alapján: \[\displaystyle p_2=\frac{1}{2},\quad p_3=\frac{3}{4},\quad p_4=\frac{5}{8},\quad p_5=\frac{11}{16}.\]
Tehát a keresett valószínűség \(\frac{11}{16}\).
8. feladat. Atom Anti egy oktaéder élein bandukol, és percenként megy át egy adott csúcsból egy szomszédosba, egyenlő eséllyel választva a lehetőségek közül.
Mennyi a valószínűsége, hogy \(k\) perc elteltével abban a csúcsban tartózkodik, ahonnan elindult?
Megoldás.
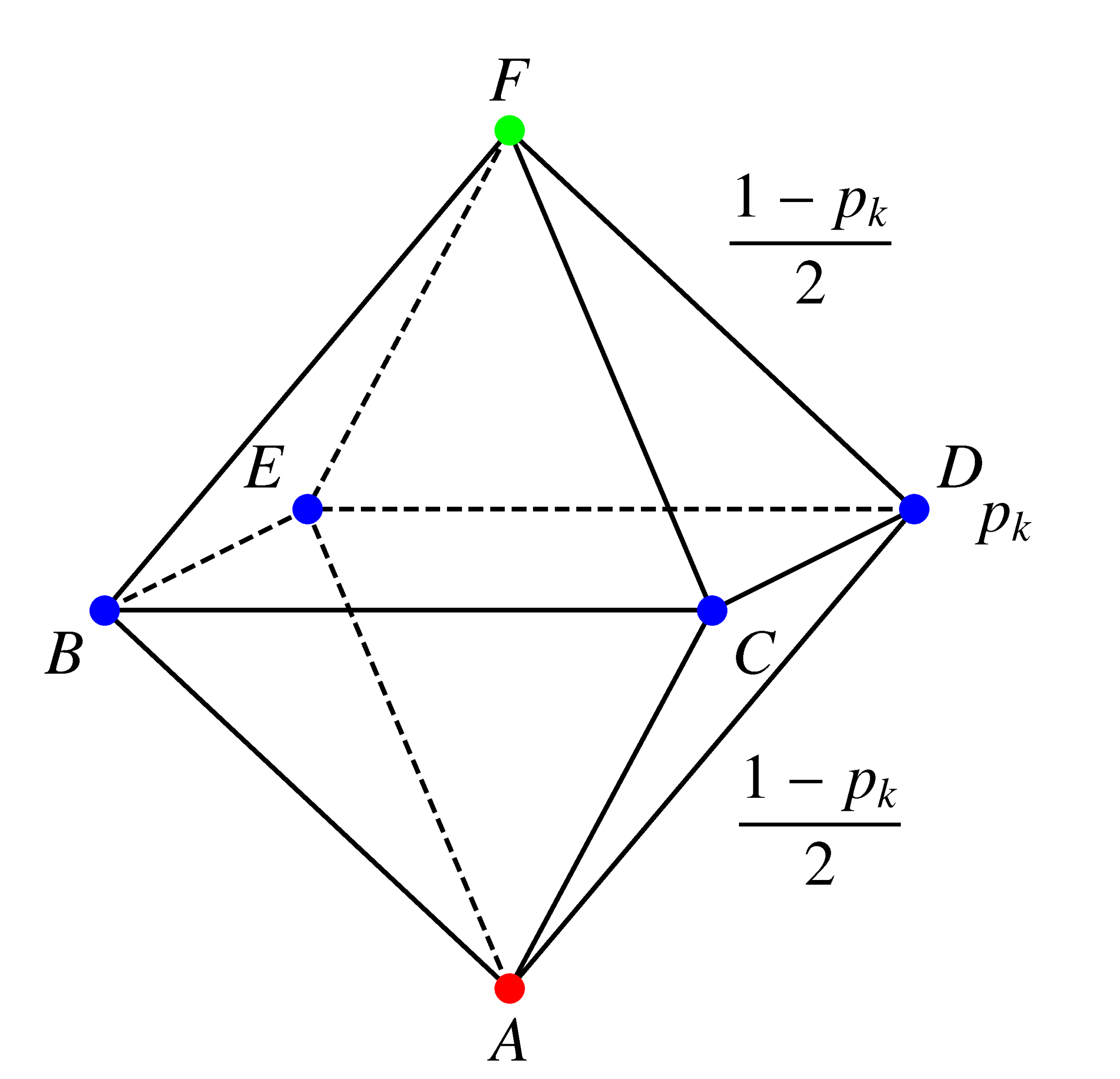
Az általánosság megszorítása nélkül feltehetjük, hogy Anti az \(A\) csúcsból indul.
Jelölje \(p_k\) annak esélyét, hogy Anti a \(k\)-adik perc végén \(A\)-val szomszédos csúcsban van ( \(k\in \mathbb{N}\)). Ekkor az előző feladat alapján: \[\displaystyle p_1=1,\qquad p_{k+1}=1-\frac{p_k}{2}.\] A \[\displaystyle \lim\limits_{k\to \infty}p_{k+1}=\lim\limits_{k\to \infty}p_k=x\] egyenlőség alapján: \[\displaystyle x=1-\frac{x}{2},\] \[\displaystyle x=\frac{2}{3},\] \[\displaystyle p_{k+1}-\frac{2}{3}=-\frac{1}{2}\left(p_k-\frac{2}{3}\right).\]
A kapott egyenlőség alapján a \(\left(p_k-\frac{2}{3}\right)\) sorozat olyan mértani sorozat, amelynek első tagja \(p_1=1-\frac{2}{3}=\frac{1}{3}\), hányadosa \(q=-\frac{1}{2}\). Ennek figyelembevételével: \[\displaystyle p_k-\frac{2}{3}=\frac{1}{3}\cdot \left(-\frac{1}{2}\right)^{k-1}=-\frac{2}{3}\cdot \left(-\frac{1}{2}\right)^k,\] \[\displaystyle p_k=\frac{2}{3}-\frac{2}{3}\cdot \left(-\frac{1}{2}\right)^k.\]
Mivel az \(A\) és az \(F\) pontok az \(A\)-val szomszédos csúcsokhoz képest szimmetrikusan helyezkednek el, ezért annak esélye, hogy Atom Anti a \(k\)-adik perc végén \(A\)-ban tartózkodik: \[\displaystyle \frac{1-p_k}{2}=\frac{1}{6}+\frac{1}{3}\cdot \left(-\frac{1}{2}\right)^k.\]
🟉
Ez az írás a 2024-ben a békéscsabai Rátz László Vándorgyűlésen elhangzott szemináriumi foglalkozás alapján készült. A közölt feladatok azt próbálják meg bemutatni, hogy miként lehet a szakköri munkában érdekes, egymásra épülő, egyre nehezedő feladatokat feladni a tanulóknak úgy, hogy azokkal ösztönözzük őket arra, hogy maguk is vessenek fel újszerű kérdéseket, és ezzel elinduljanak az önálló felfedezés útján.
A cikk folytatásában három feladatcsokorral fogunk foglalkozni. Az elsőben nem szabályos dobókockára nézünk feladatokat, a következő a geometriai valószínűséggel kapcsolatban tartalmaz majd feladatokat, végezetül játékok nyerő stratégiájának esélyét határozzuk meg.
Fonyó Lajos – Fonyóné Németh Ildikó
Keszthely








