- 2026/1
- Szerkesztő
2026 januárja a matematika hónapja a Magyar Tudományos Akadémián. A jan. 5-i kiállítás megnyitója után jan. 9-én került sor a Matematikai Társulat, a KöMaL, a tehetséggondozó rendszer és a nemzetközi diákolimpiák bemutatására, és a Bolyai Társulat 2025. évi díjainak átadására.
- 2025/4.
- Pálfy Péter Pál
Minden érdeklődőt várnak a Magyar Tudományos Akadémia székházában az MTA Matematikai Tudományok Osztályának ünnepi rendezvényein 2026. január 5.-től 29.-ig. Nemcsak előadások, de kiállítás, filmvetítések is színesítik a sűrű programot.
- 2026/1
- Simonovits András
Talán még nem hallottak arról, hogyan tette Hilbert valóban axiomatikussá az euklideszi geometriát, és hogyan akarta logikailag megalapozni az egész matematikát. És arról, hogy az általános relativitáselmélettől kezdve a kvantummechanika születéséig szinte mindenütt ott volt, – beleértve a számítástudományt is – ahol a jövő született.
- 2025/4.
- Szerkesztő
2025. december 10-én a 200 éves jubileumát ünneplő Magyar Tudományos Akadémia dísztermében 25. alkalommal adták át a Rátz Tanár Úr Életműdíjakat reáltárgyakat tanító kiemelkedő pedagógusoknak. A 8 díjazott között volt az országosan is jól ismert, a matematikatanítást egész életében szívügyének tekintő Kántor Sándorné és Pintér Klára. Gratulálunk nekik és a többi kitüntetettnek!
- 2025/4.
- Róka Sándor
A Héttusa 11. fordulójának feladatain gondolkodhatnak olvasóink a karácsonyi szünetben, hiszen a beküldési határidő 2026. január 5. A feladatok kérdéseire a feladat sorszámát és a választ bárki beküldheti a hettusa@ematlap.hu email címre. Nyitóképünket a csillagos égbolt és 77. feladat ihlette.
- 2025/4.
- Richard E. Borcherds
A Monstrum csoport elemeinek száma körülbelül megegyezik a Jupiter elemi részecskéinek számával. Mérete miatt szokták nevezni Szörnynek vagy Barátságos Óriásnak is. Aki meg szeretné ismerni, annak tudnia kell egyet s mást csoportelméletből, amihez érdemes megnézni a fordító, Maróti Attila megjegyzését az írás végén.
- 2025/4.
- Csapodi Csaba, Bereczki Ildikó, Jánvári Zsuzsanna, Kiss Anna, Kulman Katalin, Móricz Márk, Paulovics Zoltán
Pillanatkép a mesterséges intelligenciáról, hibázhatnak-e a kutatók, interaktív játékok matekórákra, tanítási segédanyagok, foglalkozások, MI-módszertan, „így tanítanánk mi”, és játékok minden mennyiségben – ez mind az idei novemberi Varga Tamás Módszertani Napokon!
- 2025/4.
- Dombi Péter
A Héttusa 65. feladatának nyomán született írás a geometriáról áttér halmazokra, majd irányított gráfokra, végül Lyndon-szavakra. A Lyndon-szavak felbukkannak az algebra, számelmélet és topológia különféle kérdéseiben, és megjelennek egészen távoli alkalmazási területeken: a számítástudománytól és kriptográfiától kezdve az elméleti fizikán és zenetudományon át egészen a molekuláris biológiáig. Nyitóképünkön Roger Lyndon (a második fotó Halmos Pál felvétele).
- 2025/4.
- Stipsicz András
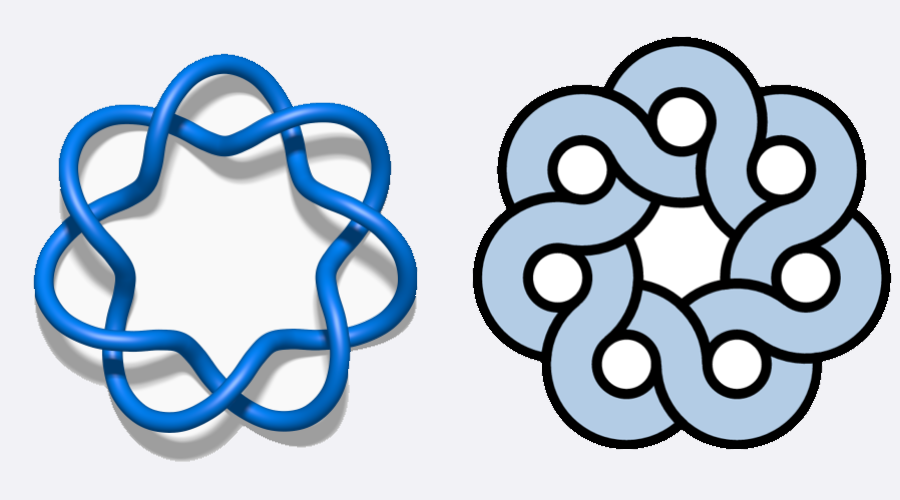
Ha valaki még nem tudja, mi is egy matematikai értelemben vett csomó, Stipsicz András ismeretterjesztő cikkéből könnyen megtanulhatja. Néhány egyszerű, csomókra vonatkozó fogalom és művelet bevezetése után kiderül egy nemrég felfedezett és meglepő válasz egy klasszikus csomóelméleti kérdésre.
- 2025/4.
- Orbán Petra
Az első magyar női matematikus akadémikus, akit külföldön is a matematikai logika, a rekurzív függvények úttörőjeként tartottak számon, egyaránt volt tudós, (tan)könyvíró, a matematika tanításának elkötelezettje, és mindig szenvedélyesen és önzetlenül kiállt igazsága mellett.
Ajánlott cikkek
Hírlevél
- 2026/1
- Szerkesztő
2026 januárja a matematika hónapja a Magyar Tudományos Akadémián. A jan. 5-i kiállítás megnyitója után jan. 9-én került sor a Matematikai Társulat, a KöMaL, a tehetséggondozó rendszer és a nemzetközi diákolimpiák bemutatására, és a Bolyai Társulat 2025. évi díjainak átadására.
- 2025/4.
- Pálfy Péter Pál
Minden érdeklődőt várnak a Magyar Tudományos Akadémia székházában az MTA Matematikai Tudományok Osztályának ünnepi rendezvényein 2026. január 5.-től 29.-ig. Nemcsak előadások, de kiállítás, filmvetítések is színesítik a sűrű programot.
- 2025/4.
- Szerkesztő
2025. december 10-én a 200 éves jubileumát ünneplő Magyar Tudományos Akadémia dísztermében 25. alkalommal adták át a Rátz Tanár Úr Életműdíjakat reáltárgyakat tanító kiemelkedő pedagógusoknak. A 8 díjazott között volt az országosan is jól ismert, a matematikatanítást egész életében szívügyének tekintő Kántor Sándorné és Pintér Klára. Gratulálunk nekik és a többi kitüntetettnek!
- 2025/4.
- Kovács Benedek, Lenger Dániel
Budapest, Kecskemét, Gödöllő és Szeged kiváló iskoláiból érkeztek a hatfős MEMO diákolimpiai csapat 11. osztályos tanulói, akik 2025. augusztusában Chemnitzben versenyeztek, egy arany-, két ezüst-, egy bronzérmet és két dicséretet szerezve. A diákok élménybeszámolójából kiderül, mi minden történt még azon a héten.
- 2025/4.
- Paulovics Zoltán
A felfedeztető matematikatanítás és Loyolai Szent Ignác (képünkön: Otros Santos: San Ignacio de Loyola) lelkiségét követő pedagógiájának párhuzamairól szóló korábbi beszélgetésünk folytatásában Németh Anna, a miskolci Fényi Gyula Jezsuita Gimnázium matematikatanára hasznos gyakorlati tanácsokat és matekfeladatokat is megoszt olvasóinkkal. Mit jelent a harmónia megléte? Baj, ha az órai játék valamiért nem sikerül?
- 2025/3.
- Paulovics Zoltán
Az Érintő 2025 márciusi számában Németh Annával – aki közel 30 éve a miskolci Fényi Gyula Jezsuita Gimnázium matematikatanára – beszélgettünk életútjáról, innovatív, felfedeztető tanítási stílusáról, aktuális nehézségeiről, kérdéseiről „A tapasztalatból születő gondolat” című interjúban. Már akkor is felmerült, hogy jó lenne alaposabban körüljárni a felfedeztetés és az iskolájában alkalmazott, ignáci pedagógia hasonlóságait, különbségeit...
- 2025/4.
- Csapodi Csaba, Bereczki Ildikó, Jánvári Zsuzsanna, Kiss Anna, Kulman Katalin, Móricz Márk, Paulovics Zoltán
Pillanatkép a mesterséges intelligenciáról, hibázhatnak-e a kutatók, interaktív játékok matekórákra, tanítási segédanyagok, foglalkozások, MI-módszertan, „így tanítanánk mi”, és játékok minden mennyiségben – ez mind az idei novemberi Varga Tamás Módszertani Napokon!
- 2025/4.
- Trembeczki Csaba
Fantasztikus a Táncsicsba járni ma is, tanárként részt venni ebben a folyamatban még annál is csodálatosabb érzés. Látni, ahogy a diákjaink évről évre fejlődnek. Segíteni őket mindenben tanárként, osztályfőnökként, szinte barátként. Megélni napról napra ezt az alkotómunkát az ország – szerintünk biztosan(!) – egyik legjobb matematika-fizika-informatika munkaközösségében itt, a Kaposvári Táncsics Mihály Gimnáziumban.
- 2025/4.
- Richard E. Borcherds
A Monstrum csoport elemeinek száma körülbelül megegyezik a Jupiter elemi részecskéinek számával. Mérete miatt szokták nevezni Szörnynek vagy Barátságos Óriásnak is. Aki meg szeretné ismerni, annak tudnia kell egyet s mást csoportelméletből, amihez érdemes megnézni a fordító, Maróti Attila megjegyzését az írás végén.
- 2025/3.
- Gyenge Ádám
A modern matematika nagy fejezetei nőttek ki a 100 éve meghalt Felix Klein gondolatai nyomán, beleértve Klein Erlangen-programját, valamint a Lie-csoportok és Lie-algebrák jelentős területeit. Míg sokáig úgy tűnhetett, hogy a szimmetriák diszkrét és folytonos csoportjainak vizsgálata messze esik egymástól, a későbbi kutatások határozottan közelebb hozták ezt a két területet.
- 2025/4.
- Róka Sándor
A Héttusa 11. fordulójának feladatain gondolkodhatnak olvasóink a karácsonyi szünetben, hiszen a beküldési határidő 2026. január 5. A feladatok kérdéseire a feladat sorszámát és a választ bárki beküldheti a hettusa@ematlap.hu email címre. Nyitóképünket a csillagos égbolt és 77. feladat ihlette.
- 2025/4.
- Róka Sándor
A Héttusa 2025. szeptemberi feladataira a megszokott versenyzőink küldték el megoldásaikat. Biztatjuk azokat is, akik eddig csak otthon gondolkodtak Róka Sándor érdekes és talán nem is túl nehéz kérdésein, írják meg az általuk helyesnek gondolt válaszokat, hiszen a Héttusa versenyébe bárki bármikor bekapcsolódhat!
- 2025/4.
- Zsák Zoltán
Zsák Zoltán gépészmérnök egy új geometriai alakzatot, sőt alakzatcsaládot mutat be, amelyeket excentoidoknak nevezett el Bár az ötlet az ipari robotokat alkalmazó automata rendszerektől indult el, de ezek a szép térformák helyet kaphatnak a szobrászatban, az építészetben vagy ékszerek tervezésénél is.
- 2025/3.
- Berend Gábor, Csendes Tibor, Gencsi Mihály, Németh T. Enikő
Naponta százával bombáz bennünket hirdetésekkel és hírekkel a média, különösen sok érkezik az internetes közösségi platformokon. Jelentős részük valódinak tűnik, de nem az. Hogyan tudjuk kiszűrni, mi álhír és mi nem?
- 2026/1
- Simonovits András
Talán még nem hallottak arról, hogyan tette Hilbert valóban axiomatikussá az euklideszi geometriát, és hogyan akarta logikailag megalapozni az egész matematikát. És arról, hogy az általános relativitáselmélettől kezdve a kvantummechanika születéséig szinte mindenütt ott volt, – beleértve a számítástudományt is – ahol a jövő született.
- 2025/4.
- Backhausz Ágnes
A jövővel kapcsolatos lehetőségek elképzelése és a valószínűségük megbecslése kulcsfontosságú mindennapi életünk megszervezéséhez, illetve hosszabb távú céljaink eléréséhez. Keszthelyi Gabriella idén megjelent könyve azt mutatja be, milyen gondolkodási lépéseket végzünk ilyenkor, hogy mindennek mi a matematikai és tudománytörténeti háttere, illetve mik azok az esetek, amikor az intuíciónk nem vezet helyes eredményre. A könyvet egyaránt ajánljuk középiskolás diákoknak, tanároknak, illetve egyetemi hallgatóknak a témában való elmélyüléshez.
Hírlevél