A geometriában az egyik legtermészetesebb kérdés, hogy két pont között melyik a legrövidebb út. Igaz-e, hogy két pont között a legrövidebb az egyenes?
A válasz az euklideszi síkon vagy térben természetesen igen, ha úgy definiáljuk az „egyenest”, hogy az a távolságot minimalizáló görbe. Ekkor a minimalizáló „egyenes” tényleg az egyenes. De az is természetes, hogy vannak olyan esetek, amikor a távolságot minimalizáló görbe nem az egyenes. Például a gömbfelületen, ahol a minimalizáló görbék körívek lesznek. Nem is akármilyen körívek, hanem az úgynevezett főkörívek, amelyek sugara a gömb sugarával egyezik meg. Itt egyébként egy érdekes jelenséggel is találkozhatunk: az egy pontból kiinduló széttartó „egyenesek” széttartása lelassul és egy idő után elkezdenek összetartani. Ez egy jellemző tulajdonsága a pozitív görbületű felületeknek. Ez a viselkedés pontosan az ellentéte az úgynevezett negatív görbületű felületeknek, ahol az „egyenesek” széttartása növekszik:
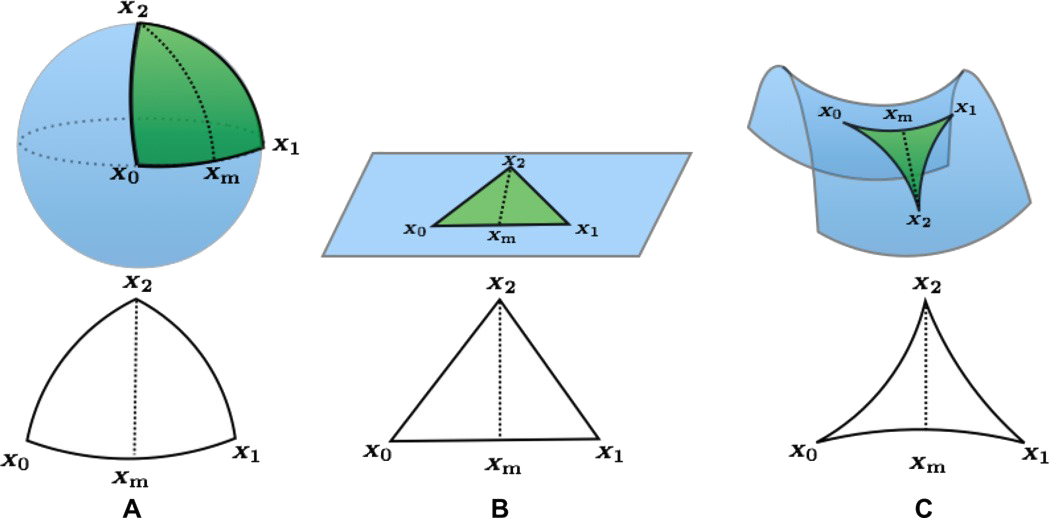
A fenti ábra A és C példájában az alapul vett felület eleve görbült volt, így a rajta haladó „egyeneseknek” is görbülniük kellett. De el tudunk-e képzelni egy olyan világot, ahol az alapul vett tér lapos, mégis az „egyenesek” nem egyenesek, hanem görbe vonalak? Képzeljük el, hogy a világegyetem egy lapos körlap! A körlap szélén rendkívül hideg van (abszolút nulla fok), a közepén viszont meleg. Jelentősen eltúlozva vegyük figyelembe a hőtágulást: a körlap széle felé haladva a testek mérete a lehűléssel tartson a nullához. Mi lesz az optimális stratégia, ha az \(A\) pontból át szeretnénk menni a \(B\) pontba?
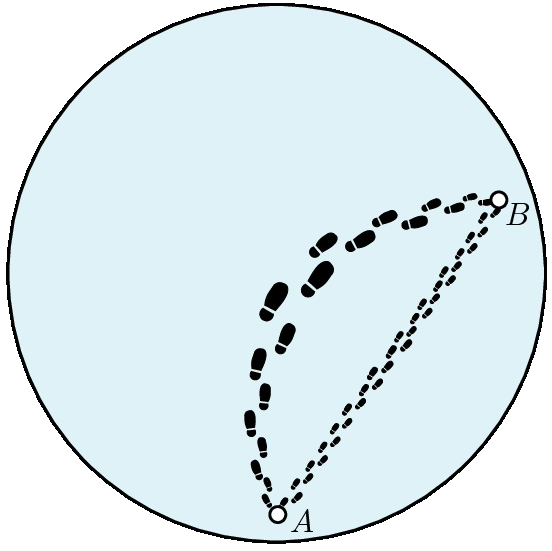
Természetesen az egyenes vonalon átmehetünk egyik pontból a másikba, de ez azzal jár, hogy végig a hideg területen gyalogolunk. Megmutatható, hogy hamarabb átérünk \(A\)-ból \(B\)-be, ha \(A\)-ból először a világunk melegebb belseje felé vesszük az irányt és így folyamatosan felmelegedve és kitágulva \(B\) pont felé kanyarodunk. Érdekességként megjegyezzük, hogy az egy pontból kiinduló „egyenesek” széttartása gyorsul, ami azt jelenti, hogy az így kapott tér görbülete negatív. A megfelelő hőtágulási viszonyokat beállítva ebben a térben a Bolyai János által felfedezett hiperbolikus geometria világa lesz érvényes.
A fenti példa egy fontos tényre világít rá: az „egyenesek” viselkedése, és így a tér geometriai jellege (görbülete) megváltozhat azzal, ha a távolságmérés megváltozik. Az előző példában ugyanis pontosan ez történt: egységnyi idő alatt más-más távolságra juthatunk el attól függően, hogy milyen irányban indultunk. Ilyen jelenségre számos példát találhatunk a gyakorlati életben. A cikk apropója Fa Nándor kiváló sportteljesítménye a Vendée Globe földkerülő vitorlás versenyen. A rendkívül nehéz fizikai igénybevétel mellett a verseny nehézsége többek között abból áll, hogy meg kell tervezni az optimális útvonalat úgy, hogy a szél alapvetően befolyásolja a távolságmérést (adott pontokban az időegység alatt elérhető pontok halmazát), és így a tér geometriáját. Az eredmény egy igen bonyolult tér, amelynek azonban kiterjedt szakirodalma van (Zermelo navigációs probléma, Randers-típusú Finsler-terek elmélete).
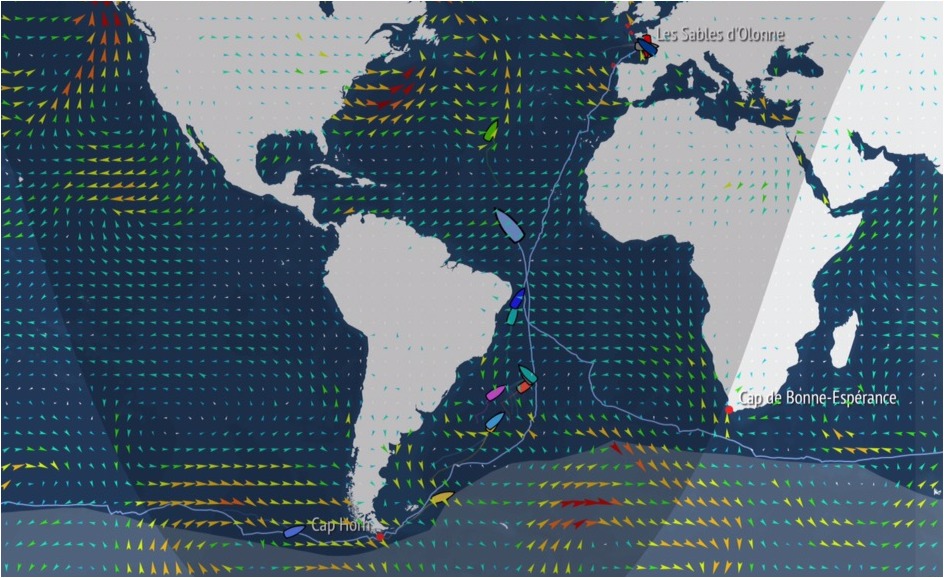
A geometriai görbület fogalmával érdekes módon a tudomány sok egyéb területén is találkozhatunk. Természetes módon jelenik meg a fizikában, csillagászatban, de találkozhatunk alkalmazásokkal a földrajz, biológia és a közgazdaságtan területén is.
Aki szeretne többet megtudni a cikkben szereplő geometriákról, annak ajánljuk Lánczos Kornél [4] könyvét, illetve az [5] és [6] cikkeket.
Muzsnay Zoltán
Irodalomjegyzék
[1] Sandhu, R. S., Georgiou, T. T., Tannenbaum, A. R.: Ricci curvature: An economic indicator for market fragility and systemic risk, Sci. Adv. 27, 2016: Vol. 2, no. 5, e1501495
[2] Fa Nándor honlapja: http://spiritofhungary.hu
[3] Vendée Globe földkerülő vitorlás verseny honlapja: http://www.vendeeglobe.org/
[4] Lánczos K.: A geometriai térfogalom fejlődése: A geometriai fogalmak fejlődése Püthagorasztól Hilbertig és Einsteinig, Budapest, Typotex, 2010
[5] Hiperbolikus geometria: https://hu.wikipedia.org/wiki/Hiperbolikus_geometria
[6] Zermelo navigációs problémája: https://en.wikipedia.org/wiki/Zermelo’s_navigation_problem
A bevezető kép készítője Fa Nándor indulásáról a Vendée Globe versenyén Eric Houdas, forrása: https://upload.wikimedia.org/wikipedia/commons/0/01/Nandor_Fa_%288%29_cropped.jpg