2024. júniusában jelent meg az Egy Schweitzer-feladat megoldása középiskolás eszközökkel. Ennek bevezetőjét érdemes elolvasni, mielőtt rátérnénk a mostani cikk nem kevésbé érdekes feladatának megoldására. A júniusi számban megjelent cikk folytatásaként ismét egy első látásra ijesztő, de középiskolások számára is érthető Schweitzer-feladat megoldását fogjuk taglalni. Az előző részben részletesen beszámoltam a verseny múltjáról és jellegzetességeiről. Bár a feladat megfogalmazásából az sejlik, hogy kőkemény egyetemi szintű tudásra lesz szükség a megoldásához, ez koránt sincs így: a mátrix megnevezés félrevezető ebben a helyzetben, a probléma semmiféle tudást nem igényel a mátrixok elméletéből. A bizonyítás tisztán kombinatorikai, és elegendő mátrixok helyett táblázatokra gondolni, amelyeknek minden cellájába 0 vagy 1 van írva. Lássuk is a példát!
Feladat. (Schweitzer, 2018/3.) Egy \(n \times n\)-es mátrixot jólfésültnek hívunk, ha minden eleme 0 vagy 1, és nem tartalmazza az \(\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}\) mátrixot részmátrixként. Lássuk be, hogy van olyan \(c>0\) konstans, amelyre teljesül, hogy bármely \(n \times n\)-es jólfésült mátrixnak van olyan, legalább \(cn \times cn\)-es részmátrixa, melynek minden eleme egyforma. (Egy jólfésült mátrix tartalmazhatja a \(\begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}\) mátrixot részmátrixként.)
Megoldás. Először tisztázzuk, mit is jelent pontosan az, hogy a mátrix nem tartalmazza az \(\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}\) mátrixot részmátrixként. Részmátrixnak nem csak a folytonos \(2 \times 2\)-es résztáblázatokat nevezzük, hanem bármely 4 cellát, amelyet úgy kapunk, hogy az eredeti mátrixnak kiválasztjuk 2 sorát (\(i\). és \(j\).) és 2 oszlopát (\(k\). és \(l\).), és tekintjük ezeknek mind a 4 metszetében lévő cellákat.
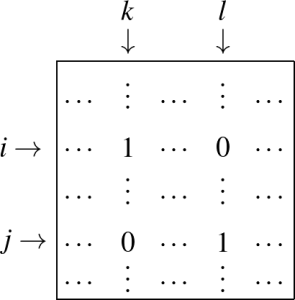
Mindezek tudatában vágjunk bele a megoldásba!
A bizonyítás a következő intuíción alapszik: ha van egy olyan sor a táblázatban, amiben „sok” (ami itt azt jelenti, hogy \(n\) valamilyen konstansszorosa) 1-es van, és ezeket ezután még „sok” 0 követi, továbbá még elegendően „sok” sor található ezen sor alatt, akkor a jólfésültségi feltételt kihasználva könnyen találhatunk egy csupa azonos elemből álló részmátrixot. Ugyanis, ha ekkor egy lejjebb lévő sorban bármelyik 1-es alatt 0 van, akkor a jólfésültségi feltétel miatt muszáj minden őt követő 0 alatt 0-nak állnia, különben találnánk egy tiltott részmátrixot, vagyis abban a lentebbi sorban is „sok” 0 lenne. Ha pedig nincs ilyen 1-es, akkor az eredeti sorunk minden 1-ese alatt 1-esnek kell állnia a lentebbi sorban.
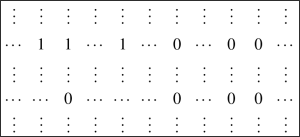
Tehát a kiválasztott sorunk alatti minden sorra igaz, hogy vagy az eredeti sor minden 1-ese alatt 1-es van, vagy az eredeti sor minden 0-ja alatt 0 van. Ha elég „sok” sor van a sorunk alatt, akkor valamelyik eset „sokszor” fog fennállni (hiszen a lentebbi sorok legalább felére ugyanaz az eset fog vonatkozni), és ezen sorokat és a hozzá tartozó megfelelő oszlopokat kiválasztva találni fogunk egy megfelelő \(cn \times cn\)-es csupa azonos elemből álló részmátrixot valamilyen \(c>0\) konstansra.
Kicsit továbbgondolva a fenti gondolatmenetet, azt is láthatjuk, hogy az is jó nekünk, ha olyan sort találunk, amelyben „sok” 0-t követ sok 1-es, csak ekkor kellően „sok” sornak kell a sorunk fölött lennie (ellentétben az előző esettel, ahol kellően „sok” sor kellett alatta), és ekkor gyakorlatilag működik ugyanaz a gondolatmenet, mint az előbb.
Ugyanakkor, ha egy sorban kellően „sok” 0 és kellően „sok” 1-es van egyszerre, akkor mindig lesz olyan szituáció, amikor „sok” 0 vagy 1 megelőzi a másik karaktert, hiszen csak megnézzük, melyikből gyűlik össze legalább a fele a konstansunknak, és utána a másiknak még mindig hátra lesz legalább a fele. Ha a mátrix közepéről indulunk ki, azt is tudjuk biztosítani, hogy amennyiben találunk egy ilyen sort, akkor alatta és felette is kellően „sok” sor legyen. Mivel a jólfésült mátrix részmátrixa is jólfésült, nekünk az teljesen megfelelő, ha a középső harmadon belül találunk megfelelő részmátrixot. Hiszen ha ehhez a középső részmátrixhoz találunk jó \(c\) konstanssal csupa azonos elemből álló részmátrixot, akkor az az eredeti mátrixhoz is jó lesz (körülbelül \(c/3\) konstanssal).
Most írjuk le mindezt matematikailag precízen!
Jelöljük a mátrixunkat \(A\)-val. Feltehetjük, hogy \(n \ge 13\) (\(n<4\) esetén választhatunk egy \(1 \times 1\)-es részmátrixot, ami triviálisan csak azonos elemekből fog állni, és ez megfelelő lesz minden \(c \le \cfrac{1}{12}\) pozitív konstansra, és a mi végső konstansunk kisebb lesz ennél). Ekkor fel tudjuk osztani az eredeti táblázatot \(3 \times 3\) darab résztáblázatra az ábrán látható módon úgy, hogy mind a 9 résztáblázatnak legalább \(\cfrac{1}{4}n\) darab sora és legalább \(\cfrac{1}{4}n\) darab oszlopa legyen (a sorokat és oszlopokat fel tudjuk 3–3 részre osztani úgy, hogy minden részben legalább \(\left\lfloor{\cfrac{n}{3}}\right\rfloor \) sor/oszlop van, és mivel \(n \ge 13\), ezért \(\cfrac{n}{4}<\cfrac{n}{3}-1<\left\lfloor{\cfrac{n}{3}}\right\rfloor\)). Nevezzük a felosztott mátrix középső részmátrixát \(B\)-nek!

Tegyük fel, hogy létezik \(B\)-nek olyan sora, amiben legalább \(\cfrac{1}{12}n\) darab 0 és legalább \(\cfrac{1}{12}n\) darab 1-es van (a bizonyítás későbbi részéből kiderül, miért választottuk pont az \(\cfrac{1}{12}\)-et itt konstansnak). Legyen ez a sor az \(i\). sor. Menjünk végig balról jobbra ezen sor elemein \(B\)-n belül, és figyeljük, hogy melyikből gyűlik össze először legalább \(\cfrac{1}{24}n\) darab!
(a) Tegyük fel először, hogy az 1-es gyűlik össze hamarabb (0-ból vagy 1-ből), és jelölje az első \(\cfrac{1}{24}n\) darab 1-eshez tartozó oszlopok halmazát \(F\). Ekkor miután összegyűlt \(\cfrac{1}{24}n\) darab 1-es, még utána kell lennie tőlük jobbra \(\cfrac{1}{24}n\) darab 0-nak (hiszen az 1-eseinkig még nem gyűlt össze belőlük \(\cfrac{1}{24}n\) darab sem, és összesen legalább \(\cfrac{1}{12}n\) van a 0-kból, úgyhogy legalább még \(\cfrac{1}{12}n-\cfrac{1}{24}n=\cfrac{1}{24}n\) darab hátra van), jelölje ezen 0-k oszlopainak halmazát \(G\).
Tekintsük a \(B\) alatti részmátrixot az \(A\) felosztásában, aminek legalább \(\cfrac{1}{4}n\) sora van a konstrukciónk szerint. Ha ezen sorok bármelyikében az \(F\) bármelyik oszlopának helyén 0 áll, akkor a \(G\) oszlopaiban ezen soron belül mindenhol 0-nak kell lennie, ugyanis ellenkező esetben találnánk egy \(\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}\) részmátrixot (mégpedig kiválasztva az \(i\). sort és ezt a sort, valamint azt az oszlopot \(F\)-ből, aminél a jelenlegi sorban 0 áll, és azt az oszlopot \(G\)-ből, aminél a jelenlegi sorban 1-es áll, megkapjuk a sértő részmátrixot).
Ez azt jelenti, hogy a \(B\) alatti részmátrix minden sora kétféleképpen nézhet ki: vagy az \(F\)-ben lévő oszlopok mindegyikének helyén 1-es áll, vagy a \(G\)-ben lévő oszlopok mindegyikének helyén 0 áll. Mivel ennek az alsó részmátrixnak legalább \(\cfrac{1}{4}n\) sora van, valamelyik lehetőség legalább \(\cfrac{1}{8}n\) sor esetén fennáll. Mivel \(F\)-ben és \(G\)-ben is legalább \(\cfrac{1}{24}n\) darab oszlop van, ezért mindkét esetben kiválasztható lesz vagy egy \(\cfrac{1}{24}n \times \cfrac{1}{24}n\)-es csupa 1 vagy csupa 0 mátrix, és ezzel ebben az esetben beláttuk a feladat állítását \(c=\frac{1}{24}\)-re.
(b) Ha először a 0-ból gyűlik össze \(\cfrac{1}{24}n\) darab a \(B\) sorában, akkor az előbbi gondolatmenetet lemásolva szintén tudunk egy legalább \(\cfrac{1}{24}n \times \cfrac{1}{24}n\)-es csupa 1-es vagy csupa 0 részmátrixot találni, csak ebben az esetben nem a \(B\) alatti, hanem a \(B\) feletti részmátrixot kell tekintenünk.
Még ennél is többet ki lehet hozni az előző módszerből: ha \(B\)-nek van olyan oszlopa, amelyben legalább \(\cfrac{1}{12}n\) darab 0 és legalább \(\cfrac{1}{12}n\) darab 1-es van, akkor analóg módon használva az előző bizonyítást, tudunk találni legalább \(\cfrac{1}{24}n \times \cfrac{1}{24}n\)-es csupa 1-es vagy csupa 0 részmátrixot, csak ebben az esetben nem a \(B\) alatti és feletti, hanem a \(B\)-től jobbra, illetve \(B\)-től balra található részmátrixot kell vizsgálnunk.
Tehát, ha \(B\)-nek van olyan sora vagy olyan oszlopa, amelyben legalább \(\cfrac{1}{12}n\) darab 0 és legalább \(\cfrac{1}{12}n\) darab 1-es van, akkor készen vagyunk. Feltehetjük tehát, hogy \(B\)-ben nincs sem ilyen sor, sem ilyen oszlop, ami viszont azt jelenti, hogy \(B\)-nek minden sorában és minden oszlopában vagy legalább \(\cfrac{1}{4}n – \cfrac{1}{12}n = \cfrac{1}{6}n\) darab 0, vagy legalább \(\cfrac{1}{6}n\) darab 1-es van.
Mivel \(B\)-nek legalább \(\cfrac{1}{4}n\) sora van, ezért találhatunk vagy legalább \(\cfrac{1}{8}n\) sort, amelyben legalább \(\cfrac{1}{6}n\) darab 0 van, vagy legalább \(\cfrac{1}{8}n\) sort, amelyben legalább \(\cfrac{1}{6}n\) darab 1-es van (vagyis, kellően sok sorban az egyik elemből nagyon sok van).
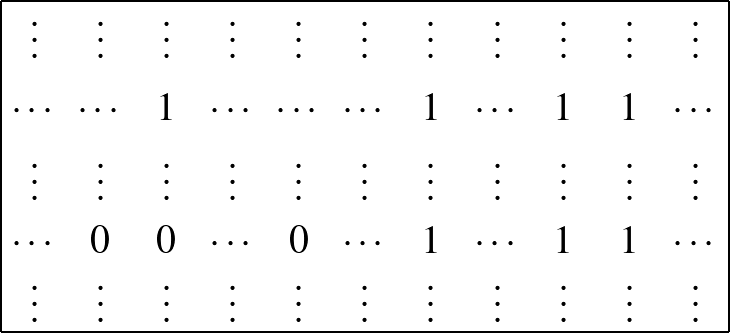
(a) Tegyük fel először, hogy a 0-s eset áll fenn, és válasszuk ki ezt a legalább \(\cfrac{1}{8}n\) darab sort \(B\)-ből, így kapjuk a \(B’\) részmátrixot. \(B’\)-ben legalább \(\cfrac{1}{8}n\) darab sor van, mindegyikben legalább \(\cfrac{1}{6}n\) darab 0, ezért \(B’\)-ben minimum \(\cfrac{1}{8}n \cdot \cfrac{1}{6}n = \cfrac{1}{48}n^2\) darab 0 elemnek kell lennie. De így az is igaz, hogy van \(B’\)-ben legalább \(\cfrac{1}{8}n\) oszlop is úgy, hogy mindegyikben legalább \(\cfrac{1}{24}n\) darab 0 van, hiszen ellenkező esetben \(B’\)-n belül kevesebb, mint \(\cfrac{1}{8}n \cdot \cfrac{1}{24}n + \cfrac{1}{8}n \cdot \cfrac{1}{8}n = \cfrac{1}{48}n^2\) darab 0 lenne, ami ellentmondás.
Válasszuk ki \(B’\)-ből ezt a legalább \(\cfrac{1}{8}n\) darab oszlopot, így kapjuk a \(B^{\prime\prime}\) mátrixot. A konstrukcióból adódik, hogy \(B^{\prime\prime}\) minden oszlopában legalább \(\cfrac{1}{24}n\) darab 0 van, de az is igaz, hogy minden sorában is legalább \(\cfrac{1}{24}n\) darab 0 van, hiszen \(B’\) minden sorában legalább \(\cfrac{1}{6}n\) darab 0 van, és mindegyikből legfeljebb \(\cfrac{1}{4}n-\cfrac{1}{8}n=\cfrac{1}{8}n\) darabot vettünk el, amikor kiválasztottuk \(B^{\prime\prime}\) oszlopait (és \(\cfrac{1}{6}n-\cfrac{1}{8}n=\cfrac{1}{24}n\)).
Tehát \(B^{\prime\prime}\) minden sorában és minden oszlopában is legalább \(\cfrac{1}{24}n\) darab 0 van. Most megint nagyon hasonló módon fogunk eljárni, mint a bizonyítás első részében: vegyük a \(B^{\prime\prime}\) mátrix bal felső negyedét, ami egy \(\cfrac{1}{48}n \times \cfrac{1}{48}n\)-es mátrix. Ha ebben csak 0 van, akkor készen vagyunk ( \(c=\cfrac{1}{48}\)- dal), ellenkező esetben pedig van egy 1-es ebben a bal felső sarokban. De ennek az 1-esnek a sorában tőle jobbra található még legalább \(\cfrac{1}{24}n-\cfrac{1}{48}n=\cfrac{1}{48}n\) darab 0 (hiszen a sorban legalább \(\cfrac{1}{24}n\) darab 0 van, és ebből a bal felső sarkunk legfeljebb \(\cfrac{1}{48}n\) darabot tartalmazhat), és ugyanúgy az is igaz, hogy ezen 1-esnek az oszlopában, alatta még található legalább \(\cfrac{1}{48}n\) darab 0. De ekkor a jólfésültség miatt ezen 0-k sorainak és oszlopainak metszetében csak 0 állhat, így ekkor találtunk egy \(\cfrac{1}{48}n \times \cfrac{1}{48}n\)-es csupa 0 részmátrixot.

(b) Ha \(B\)-ben van legalább \(\cfrac{1}{8}n\) sor, amiben legalább \(\cfrac{1}{6}n\) darab 1-es van, akkor a bizonyítás pontosan ugyanúgy megy, mint az előbb, azzal a különbséggel, hogy ekkor \(B^{\prime\prime}\)-nek nem a bal felső \(\cfrac{1}{48}n \times \cfrac{1}{48}n\)-es sarkát, hanem a jobb alsó \(\cfrac{1}{48}n \times \cfrac{1}{48}n\)-es sarkát kell tekintenünk, és ebből fogunk találni egy legalább \(\cfrac{1}{48}n \times \cfrac{1}{48}n\)-es csupa 1-es részmátrixot. □
Szőke Tamás








