Reszkető levél,
Napfény súgja: „nőj, ne félj!”
Szél csak táncba hív.
Wettl Ferenc: Lineáris algebra, TypoTeX, 2025, második kiadás, 523 oldal
https://www.typotex.hu/book/12965/linearis_algebra
Első találkozásom a lineáris algebrával sokak élményéhez hasonlított: kezdetben tartottam tőle, de idővel megszerettem. Hamar kiderült, hogy egy feszes logikájú, kristálytiszta szépségű tudományterülettel van dolgom – olyan szerkezeti renddel, amely már önmagában is lenyűgöző. Ugyanakkor már hallgatóként is éreztem benne valami különös kettősséget: az egzaktság magával ragadó vonzereje mellett ott voltak a fésületlenül széttartó alkalmazások.
A lineáris algebra világa akkor vált igazán szerethetővé számomra, amikor először tartottam gyakorlatot Wettl Ferenc tanár úr előadásaihoz, közlekedésmérnök hallgatók számára. A feladat kihívást jelentett – nemcsak a hallgatóknak, hanem nekem is. Ekkorra már mindenki tudta: Wettl Ferenc neve összeforrt a lineáris algebra oktatásával. Az előadások alapját már részben az a jegyzet képezte, amelyből később ez a könyv is született. Talán nem árulok el titkot, ha megemlítem: amikor ő tartotta a második féléves matematika előadást, a lineáris algebra rész – szinte törvényszerűen – mindig egy kicsit hosszabbra nyúlt. Nem bántuk, mert éreztük, hogy ez egy különleges, emlékezetes félév lesz.
„A lineáris algebrát nem lehet érteni” – e sokatmondó hallgatói mondat ihlette Wettl Ferenc könyvének bevezető gondolatát, és egyben annak legfontosabb célját is kijelöli: érthetővé tenni azt, amit sokan örök misztikumként élnek meg. Ezzel az ambiciózus vállalással indul útjára a tankönyv, amely nem csupán egy jegyzet a sok közül, hanem egy gondolkodásra serkentő, pedagógiai szempontból kiemelkedő kezdeményezés.[1]

A könyv koncepciója tudatosan szakít az axiomatikus kezdéssel, és az absztrakt tárgyalást a részterület univerzumát benépesítő matematikai objektumok – a lineáris algebrai bestiárium – megismerését követően illeszti be a tárgyalásba. A fogalmak, sarokkőként funkcionáló állítások motivációs hátterét keresi, ezeket gyakorlati példákkal és geometriai intuícióval támasztja alá. A didaktikai szemlélet remekül szolgálja a heterogén hallgatói csoportok igényeit, különösen azokét a tanulókét, akik a „kézzelfogható” megközelítés, a vizuális megismerés vagy az algoritmikus gondolkodás révén kísérlik meg megérteni a matematikát.
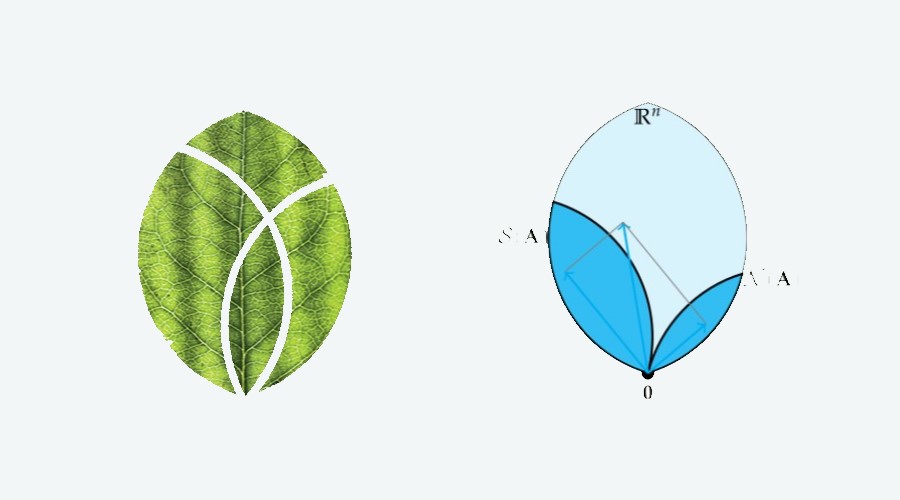
Felidézhető két alapmű, ami többé kevésbé hozzájárulhatott a Wettl által választott felépítéséhez. Az egyik Gilbert Strang Lineáris algebrája. Sokan osztozhatnak abban a véleményben, hogy Strang előadásainak húzása és értéke nem testesült meg könyveiben, és maga a Strang-féle tankönyv borzalmasan megírt matematikai munka. Ennek ellenére elvitathatalan Gilbert Strang pedagógiai módszere, amely például a nevezetes alterek ábrázolására bevezetett egymásra merőleges „téglalapokkal” operáló vizuális megoldásában érezteti erejét. Ennek egy elegánsabb és szebb vizualizációja a Wettl által választott levéldiagram. Ez a vizualizációs forma amellett, hogy szinte megszólítja a hallgatót: „Érts meg, érdemes!”, magával ragadóan vonzó látványt nyújt. Strang másik kiváló innovációja a lineáris algebra alaptétele[2], amely valójában egy elv, amely sok probléma közös logikára felfűzött megoldását kínálja a lineáris egyenletrendszer megoldásától a szinguláris érték szerinti felbontásig (SVD).

A másik nevezetes jegyzet Serge Lang csodálatos lineáris algebra könyve, amely ugyan formális-axiomatikus felépítésű, de mindig tartalmazza az adott fogalom belső, matematikai motivációját, és a képletek és eljárások természetes matematikai kérdésfeltevésekre adott természetes matematikai válaszokként vannak tálalva. Ez a tárgyalás is hatással volt Wettl könyvére, mert könyvében a didaktikai hangsúly mellett mindig megjelennek azok a világítótorony-szerű tételek, mint a Schur-tétel vagy a Jordan-tétel, amelyek az alkalmazások érdeklődést fenntartó hatása mellett nem csak előre tolják, hanem felfelé, az absztrakció irányába húzzák az olvasó érdeklődését.
Érdemes felidézni, hogy számos lineáris algebráról szóló jegyzet és tankönyv jelent meg eddig is a magyar tankönyvpiacon. Az egyik legfigyelemreméltóbb Rózsa Pál számos munkája, aki a Műegyetemen munkálkodott, és akihez a témában monumentális életmű kapcsolódik. Mind a Wettl-könyv, mind a Rózsa-könyvek átnézésében, lektorálásában nagy szerepet játszott Stubnya Gusztávné Etelka, a Műegyetem nyugalmazott adjunktusa (továbbá sokan mások, így a BME Algebra Tanszékének nagyon sok tagja járult hozzá a Wettl-könyv lektori munkájához). Az ELTE hallgatói pedig Freud Róbert Lineáris algebra című tankönyvéből tanulhattak.
Már az első oldalak megmutatják Wettl könyvének egyik legnagyobb értékét: a matematikai nyelvezet fokozatos bevezetését a középiskolai alapokra építve. A vektor fogalmát nem csupán koordinátás alakban tárgyalja, hanem olyan invariáns fogalmakkal is, mint irányított szakasz, hossz, szög, vetület, orientáció. A vektorok fejezetben az alapfogalmak világos, geometriailag is megalapozott tárgyalásán túl gondosan megválasztott alkalmazásaik is szerepelnek, mint a forgatónyomaték, a paralelepipedon térfogata vagy a statisztikából ismert korrelációs együttható lineáris algebrai értelmezése. Ezek az élő példák amellett, hogy motiválják a fogalmakat, kaput nyitnak az absztrakciók és a távoli alkalmazások felé is. Kiemelkedik a Cauchy–Schwarz–Bunyakovszkij-egyenlőtlenség tárgyalása, amely a vektortérbeli gondolkodás első mélyebb stációja.
A Gauss- és Gauss–Jordan-módszer részletes és lépcsőzetesen bevezetett algoritmikus leírása figyelemre méltó. A „lépcsős” és „redukált lépcsős” alak elvi és gyakorlati különbségének érzékeltetése különösen hasznos. Kiemelkedő az Egyenletek geometriája fejezet, ahol a sík, egyenes, hipersík – mint algebrai objektumok – két modellben is megjelennek: sor-, és oszlopmodellben. A Megoldhatóság fejezetben jelennek meg először a nevezetes alterek és az ünnepelt levéldiagram. Itt érünk el először az általánosság első szintjére és ezek a fogalmak már előre vetítik az axiomatikus tárgyalást.
A Mártixműveletek fejezetben a blokkmátrixokkal való számolás, a Kronecker-szorzat, illetve a mátrixszorzás geometriai jelentése is bekerül a tárgyalásba – amelyek más felépítésekben gyakran csak felsőbb szinteken jelennek meg. A szerző célja nyilvánvalóan az, hogy a műveleti formalizmus mögötti intuíciót is megmutassa. Ahogy Strangnál, itt is központi szerepet kap az LU-felbontás. Olyan izgalmas, távolinak ható példákat is tárgyal, mint a gráfok mátrixreprezentációja. Ebben a fejezetben kerülnek elő a rendszerváltás és modellváltás neuralgikus kérdései, talán ennek köszönhető, hogy a könyvet lefóliázott formában árulják.
A determináns igazi „próbakő” a megértés szempontjából. A szerző többféle megközelítést is alkalmaz: térfogatelemeken, permutációs nézőpontból, majd később a kifejtési tételek irányából is bemutatja. A Cramer-szabály és a determináns mint függvény kontextusba helyezése segíti elkerülni az automatikus „receptkövető” gondolkodást, amely sok tárgyalásban csak a Leibniz-formula közlésében merül ki. Különösen dicséretes tehát, hogy Wettl számára a determináns messze nem szorzatösszegek egy speciális alakja, hanem egy organikusan kialakuló, érthető fogalom. Itt érződik Serge Lang hatása a könyvön.
A sajátértékek és sajátvektorok elmélete a lineáris algebra egyik központi témaköre. A diagonalizáláson és a Jordan-féle normálalak tárgyalásán túl a könyv egy izgalmas alkalmazási területre is eljut: a mátrixfüggvények világába. A szerző bemutatja, miként teszi lehetővé a diagonalizáció, hogy analitikus függvényeket is értelmezzünk mátrixokon. A mátrixfüggvények a lineáris differenciálegyenlet-rendszerek megoldásának is fontos szereplői, ezért az itt megszerzett tudás a modern mérnöki számítások egyik alapkompetenciáját is alkotják.
Az euklideszi tér absztrakt fogalmának bevezetésével a geometria és az algebra kapcsolatában új távlatok nyílnak. A merőlegesség és a vetítés általánosítása egy furcsa alkalmazáshoz, a pszeudoinverz bevezetéséhez vezet, amely az inverz fogalmának kiterjesztése nem négyzetes vagy szinguláris mátrixokra. A tankönyv ezekkel a mai eszközökkel mutatja meg, hogyan adható optimális megoldás (legjobb közelítés) akár nem konzisztens egyenletrendszerek esetén is. Az itt tárgyalt legjobb közelítés elve a lineáris regresszió matematikai alapjait is megvilágítja.
A szimmetrikus mátrixok elméletét az ortogonális diagonalizálás témaköre követi. A főtengely-transzformáció és a kvadratikus alakok vizsgálata a kúpszeletek geometriájának mélyebb megértését is elősegíti. A tárgyalás az SVD (szinguláris érték szerinti felbontás) bemutatásával teljesedik ki, amely a modern lineáris algebra egyik leghatékonyabb eszköze. Egy különleges geometriai interpretációt is kapunk: az SVD egy lineáris transzformációt forgatás/tükrözés-nyuzsorítás[3]-forgatás/tükrözés kompozícióláncként írja le, amely az egységgömböt egy ellipszoidba képezi le. Ez a tudásanyag az adattudományban, a gépi tanulás és a nagy nyelvi modellek (LLM) elméletében is nélkülözhetetlen.
A norma általános fogalmának bevezetése a lineáris algebra és a matematikai analízis kapcsolatát teszi feszesebbé, absztrakt, mégis kézzelfogható módon terjesztve ki a vektorhossz fogalmát. A nemnegatív mátrixok egy speciális, ám fontos mátrixosztályt képviselnek, amelyet a Perron–Frobenius-elmélet keretében ismerhetünk meg. A könyv érthetően, plasztikusan mutatja be a primitív és irreducibilis mátrixok tulajdonságait. A sztochasztikus mátrixok és a Markov-láncok témaköre gyakran vizsgált folyamatok matematikai modellezésébe nyújt betekintést. A szerző könnyen érthető példákon, például a „Ki nevet a végén?” című táblás játékon keresztül is szemlélteti a Markov-láncok működését.
A tankönyv tartalmi gazdagsága tehát lenyűgöző: a klasszikus témák (vektorok, mátrixok, lineáris egyenletrendszerek, determináns, sajátértékek stb.) mellett helyet kapnak olyan, a modern alkalmazások számára elengedhetetlen fejezetek is, mint például az SVD, a disztribúciók, a Fourier-mátrixok és a Markov-láncok matematikája. Ezen utóbbiak különösen értékesek a mai adattudományi és jelfeldolgozás-központú korszakban, ahol a lineáris algebra alkalmazása egyre nagyobb szerepet kap.
A könyv különösen erős abban, hogy többféle tanulási stílushoz kínál belépési pontot:
- Procedurális: részletesen kidolgozott mintapéldák, algoritmusok, számítási útmutatók segítik az elmélet gyakorlati alkalmazását.
- Vizuális: számos geometriai magyarázat és szemléltetés építi a térbeli intuíciót, amely a lineáris algebra sokszor rejtett szépségeit tárja fel.
- Számítógépes: az Octave (Matlab), ill. Python nyelvek használatával a szerző a lineáris algebra számítógépes alkalmazásai felé is hidat épít. A hallgatók így nemcsak elméletet tanulnak, hanem eszközhasználatot is.
Wettl Ferenc könyve nem pusztán oktatási segédanyag, hanem annak demonstrálása, hogy a matematika gondolkodni is tanít. Ma már nem tartok gyakorlatot a tanár úr előadásához, de van egy tárgyunk, amit közösen tanítunk a Műegyetem Villamosmérnöki és Informatikai Karának (VIK) hallgatói számára, így még mindig testközelben látom azt az elhivatottságot, ahogy a matematikát oktatja a jövő mérnökeinek. Nem véletlen, hogy a VIK egy kisebb összeggel támogatta a könyv TypoTeX-es megjelenését, amiért a matematikus közösség hálával tartozik a kar vezetésének. Magát a tankönyvet pedig nem csak Wettl Ferenc, hanem többen is alkalmazzuk az egyetem hallgatóinak oktatásban, legyenek azok villamosmérnökök vagy matematikusok. Ebből a szempontból is megerősítést nyert a könyv használhatósága, amelynek pedagógiai módszereit és didaktikai felépítését a villamosmérnök hallgatók második féléves matematika kurzusában én magam is előadóként alkalmazom. Jóllehet ennek a terjedelmes témának az egyetlen tankönyvbe integrálása szinte lehetetlen vállalkozás volt a szerző részéről, mégis a hallgatók számára az említett kurzusokban szükséges tartalom ebben a munkában mind megtalálható. A monumentális és igényesen megírt tankönyv legendás voltát az is igazolja, hogy immáron a második és valószínűleg nem az utolsó kiadását tarthatja kezében az olvasó.
Molnár Zoltán Gábor
egyetemi adjunktus
BME TTK, Matematika Intézet, Algebra és Geometria Tanszék
Irodalom
Freud Róbert (2009). Lineáris algebra. ELTE Kiadó.
Lang, S. (1987). Linear algebra. In Undergraduate texts in mathematics.
Rózsa Pál. Lineáris algebra és alkalmazásai. Műszaki Könyvkiadó, Budapest, 1974. és Tankönyvkiadó, Budapest, 1991.
Strang, G. (2023). Introduction to linear algebra. Wellesley-Cambridge Press.
Lábjegyzetek
[1] A tankönyv első kiadásáról az Érintő hasábjain már született recenzió: https://ematlap.hu/konyvespolc-ajanlo/wettl-ferenc-linearis-algebra/
[2] Az A mátrix sortere és nulltere merőleges kiegészítő alterek. Eszerint a sortér bármely vektora merőleges a nulltér bármely vektorára, és az n dimenziós tér bármely vektora egyértelműen felbomlik egy sortérbe és egy nulltérbe eső vektor összegére.
Gilbert Strang, The Fundamental Theorem of Linear Algebra, The American Mathematical Monthly, Vol. 100, No. 9. (Nov., 1993), pp. 848–855. https://www.engineering.iastate.edu/~julied/classes/CE570/Notes/strangpaper.pdf
[3] nyújtás és zsugorítás