Beszámoló a 11. fordulóról
Ebben a fordulóban 11-en küldtek válaszokat, megoldásokat, összesen 64 helyes választ. Heten adtak mind a 7 feladatra hibátlan választ. A táblázat fejléce a feladatok számát mutatja, a színes cellák pedig a jó válaszokat.
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | |
|---|---|---|---|---|---|---|---|
| Makay Géza | |||||||
| Udvari Tibor | |||||||
| Dombi Péter | |||||||
| Turchányi Gyula | |||||||
| Deli Lajos | |||||||
| Berkó Erzsébet | |||||||
| Szemerédi Ferenc | |||||||
| Izsák Beatrix | |||||||
| megérek egy petákot | |||||||
| Kallós Béla | |||||||
| Sógor Tamás |
Fordulónként a legjobb megoldók közül néhányan könyvjutalmat kapnak. A legújabb jutalmazottak Izsák Beatrix és Kallós Béla, ők a Typotex és a MATEGYE Alapítvány könyveit választották:
\(\bullet\) Keszthelyi Gabriella: Milyen színű a valószínű?
\(\bullet\) Orosz Gyula: Hibás feladatmegoldások a középiskolában
Megoldások, megjegyzések a Héttusa 11. fordulójának feladataihoz
71. Az \(1, 2, 3, \dots, 20\) számok felírhatók-e olyan sorrendben, hogy két vagy több szomszédos szám átlaga sose legyen egész szám?
Válasz. Van ilyen sorrend.
Dombi Péter megoldása: Vegyük észre, hogy \(d\) egymás utáni szám összege mindig osztható \(d\)-vel, ha \(d\) páratlan (a középső szám a számok átlaga), és sosem osztható \(d\)-vel, ha \(d\) páros (mert az átlag a két középső szám közé esik).
Legyen \[\displaystyle a_i=\begin{cases} i,&\text{ha \(i\) páratlan}\\ i+2,&\text{ha \(i\) páros.} \end{cases}\]
Ekkor az \(a_i (i=0,1,2,\cdots)\) sorozat meg fog felelni a feladat feltételének.
Ugyanis, ha \(d\) páros, akkor egy \(d\) hosszúságú ablakban minden második szám \(2\)-vel, azaz az összeg pontosan \(d/2\cdot 2=d\)-vel növelt, így az továbbra sem osztható \(d\)-vel.
Ha pedig \(d\) páratlan, akkor az összeg majdnem \(d\)-vel változik: \(2\cdot\lfloor d/2\rfloor=d-1\)-gyel, vagy \(2\cdot\lceil d/2\rceil=d+1\)-gyel nő – aszerint, hogy páratlan vagy páros túlsúly van az ablakon belül –, így az \(d\)-vel osztva \(\pm 1\)-et ad maradékul. Tehát a \[\displaystyle 2, 1, 4, 3, 6, 5, \dots, 20, 19\] sorozat valóban megfelelő.
Megjegyzések. Igaz az állítás 20 helyett más páros számra is, míg páratlan számokra nem igaz. Ha a 20 számot egy körön helyezzük el, akkor sem igaz az állítás.
72. Egy körön kijelöltünk 100 különböző pontot, és ezekhez odaírtuk az \(1, 2, \dots, 100\) számokat valamilyen sorrendben. Igaz-e, hogy a számok párosíthatók úgy, hogy a párba állított számok összege páros, és a hozzájuk tartozó pontokat összekötő 50 szakasz nem metszi egymást?
Válasz: Nem igaz. Létezik olyan számozás, hogy bármilyen párosítás esetén lesznek metsző szakaszok.
Makay Géza megoldása: A feltételek szerint páros számokat párosakkal, páratlanokat páratlanokkal kell összekötni. Ha felváltva páros és páratlan számokat írunk, akkor bármelyik szám és párja olyan, hogy a kört úgy osztják két részre, hogy mindkét felén páratlan sok szám lesz. Így kell legyen egy pár, ami a kör két különböző felén van, tehát az azok által meghatározott szakasz metszi az eredeti pár által meghatározott szakaszt.
De természetesen el lehet helyezni és össze lehet kötni a számokat úgy, hogy a szakaszok ne metsszék egymást: ha először a páratlanokat írjuk fel és utána a párosokat, és minden számot a (megfelelő) szomszédjával kötjük össze, akkor azok nem fogják metszeni egymást.
Turchányi Gyula példája: Helyezzük el a számokat úgy, hogy a felső félköríven legyen 49 db páros szám, az alsó félköríven pedig az összes páratlan szám (50 db) és középen közéjük ékelve a megmaradt 1 db páros szám.
A magányos páros számnak (hogy az összeg páros legyen) a felső íven lévő egyik páros számhoz kell csatlakoznia. Ez a húr falszerűen kettévágja a kört. A fal egyik oldalán marad 25 db páratlan szám. Mivel páratlant csak páratlannal köthetünk össze, 12 pár létrejötte után marad 1 db „árva” páratlan szám, amelynek a párja a fal túloldalán van. Ennek az összekötő szakasznak metszenie kell a falat.
Megjegyzés. Emlékeztetőül az előző forduló hasonló feladata:
69. Egy körön kijelöltünk 100 különböző pontot, és ezekhez odaírtuk az \(1, 2, \dots, 100\) számokat valamilyen sorrendben.
Igaz-e, hogy a számok párosíthatók úgy, hogy a párba állított számok összege páratlan, és a hozzájuk tartozó pontokat összekötő 50 szakasz nem metszi egymást?
Válasz: Igaz.
73. Adott egy kör belsejében 10 pont, amelyek között nincs három egy egyenesre eső. Igaz-e, hogy a pontok mindig párosíthatók úgy, hogy a párba állított pontokra illeszkedő egyenesek mindegyike metszi a többi egyenest a kör belsejében?
Válasz: Igaz.
Megoldás. A párokat összekötő szakaszok összhossza alapján azt a páronkénti összekötést választjuk, amikor ez maximális. Ekkor bármely két egyenes metszi egymást a kör belsejében.
Tegyük fel, hogy mégsem. Az \(AB\) és \(CD\) szakaszok egyenesei a körön kívül metszik egymást. Ez a négy pont egy \(ABCD\) konvex négyszöget alkot.
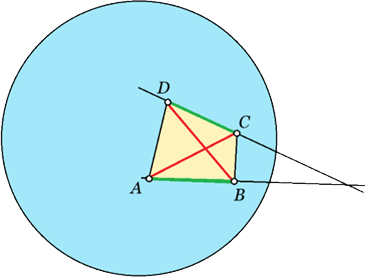
Ekkor \(AC+BD>AB+CD\), így mégsem maximális a választott összekötés, hiszen az \(AB\) és \(CD\) szakaszok helyett \(AC\)-t és \(BD\)-t választva a szakaszok összhossza nőtt.
Az ellentmondás az állításunkat igazolja.
Megjegyzés. Emlékeztetőül az előző forduló hasonló feladata:
67. A síkon adott \(20\) különböző pont, amelyek között nincs három egy egyenesre eső. Igaz-e, hogy a pontok párosíthatók úgy, hogy a párba állított pontokat összekötő 10 szakasz mindegyike metszi a többi szakaszt?
A válasz: Nem igaz.
74. Egy \(8\times 8\)-as táblázat celláiba egy-egy számot írtunk, az \(1\) és \(-1\) számokat úgy, hogy a 64 szám összege nulla. Igaz-e, hogy a táblázat a rácsvonalak mentén két darabra vágható úgy, hogy a tábla mindkét darabjában nulla a számok összege?
Válasz: Igaz.
Dombi Péter megoldása: Mivel a vágás utáni darabok méretére, alakjára nincs megkötés (csak a számukra!) ezért egy \(1\times 2\)-es dominó alakú téglát fogunk a tábla széléről „letörni”. A tábla szélén 28 cella van, ha ezek közt van \(+1\) és \(-1\) is, akkor a tábla szélén haladva a két cellát összekötő úton lesz két szomszédos, ellenkező előjelű számot tartalmazó mező, így az a dominó megfelelő lesz.
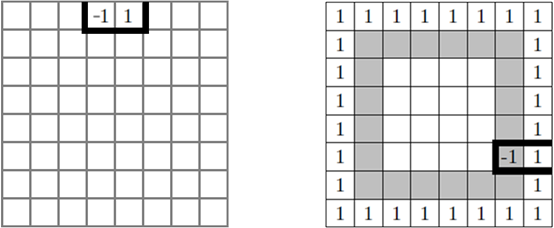
Ha a tábla peremén minden cella azonos előjelű, akkor az eggyel beljebb haladó gyűrű 20 cellája közül biztosan lehet egy ellenkező előjelűt kiválasztani, hiszen a 64 cellából 32–32 kell hogy azonos előjelű legyen. Az a vele szomszédos szélső cellával egy, a táblaszélre merőleges, \(0\) összegű, \(1\times 2\)-es dominót fog alkotni.
Makay Géza megoldása: Igen. Csak akkor lehet \(0\) az összeg a cellák egy halmazában, ha az a halmaz páros sok cellát tartalmaz. Nyilván lesz két oldalszomszédos mező, hogy az egyikben \(1\) a másikban \(-1\) van, ha ezt a részt kivágjuk a táblázatból, akkor az megfelelő vágás lesz.
De olyan vágás is van, amelyik esetén mindkét részben 32 mező van, nem „lyukat” vágunk a táblába, sőt a két rész középpontosan szimmetrikus képe egymásnak. Vágjuk ketté a táblát vízszintes vonallal 32–32 mezőre. Ezután egy-egy cellát hozzáadva illetve elvéve a két halmazból a vízszintes vágást függőleges vágásra tudjuk fordítani például úgy, hogy a tábla bal alsó sarkában levő 16 mezőt sorfolytonosan balról jobbra haladva hozzávesszük a „fenti” 32 mezőhöz, miközben a jobb felső sarokban lévő 16 mezőt alulról felfelé és jobbról balra haladva szintén sorfolytonosan elvesszük belőle.

A kapott függőleges vágást tovább „forgatva”, vagyis most a jobb alsó sarokban oszlopfolytonosan hozzávéve és a bal felső sarokból oszlopfolytonosan elvéve a mezőket megkapjuk az eredeti vágást, de közben a felső rész „átfordult” az alsóba és viszont.
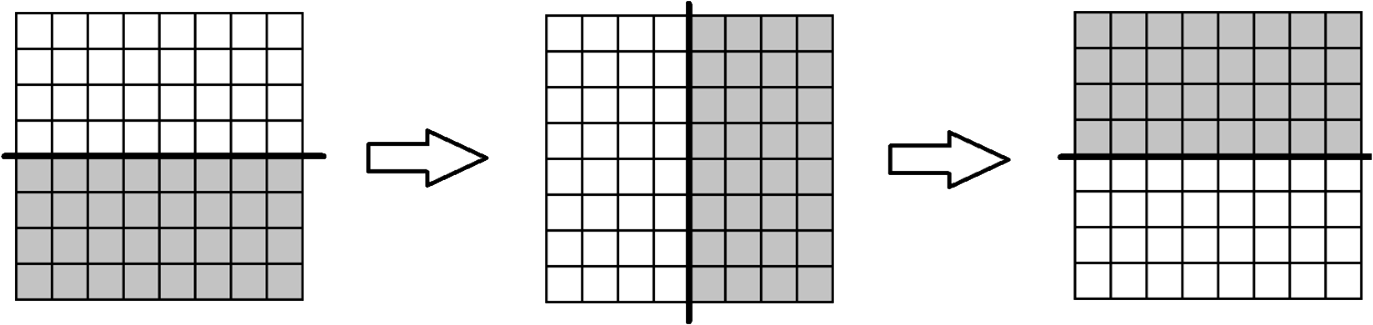
Minden lépésben igaz, hogy a két részben levő összeg páros volt és a lépések során az összegek \(0\), \(2\) vagy \(-2\) értékkel változtak. Ha kezdetben nem \(0\) volt a két részben az összeg (amikor is kész lennénk), akkor a felső összeg lehetett (mondjuk) pozitív, ami átment negatívba (vagy fordítva), tehát a lépések során valamikor \(0\) is kellett legyen.
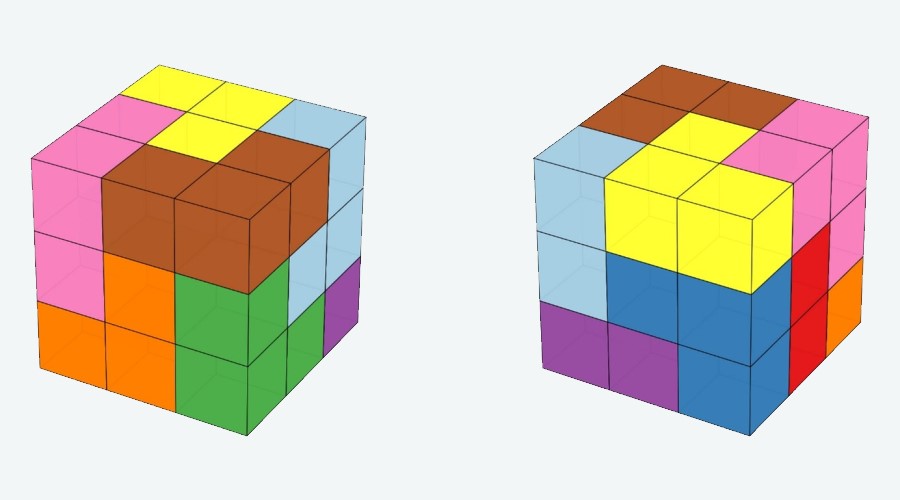
Egy érdekes kérdés lehet, hogy egy egyenes vágással meg lehet-e oldani az eredeti feladatot, de könnyű ellenpéldát konstruálni: rakjuk az összes \(1\)-est a bal alsó sarokba:

Ugyanis így akkor egy függőleges egyenes vágásnál a bal oldalon, egy vízszintesnél pedig alul mindig több \(1\)-es lesz, mint \(-1\)-es, nem lesz \(0\) az összeg.
Egy másik kérdés, hogy ha megadjuk, hogy hány (páros számú) mező legyen az egyes részekben, akkor is fel tudjuk vágni a táblát két megadott darabszámú mezőt tartalmazó részre. Ugyanis jelöljünk ki egy tetszőleges összefüggő, (az egyik) megadott darabszámú mezőt tartalmazó részt, és legyen ebben a mezőkön levő számok összege (mondjuk) pozitív. Ekkor induljunk el a \(-1\)-es számot tartalmazó mezők felé úgy, hogy egy lehetőleg \(-1\)-es számot tartalmazó mezőt vegyünk ehhez hozzá, és egy \(1\)-es számot tartalmazó mezőt vegyünk el belőle, ha ez sikerül, az összeg \(2\)-vel csökken. Ha ez nem lehetséges, akkor \(2\)-vel nő vagy nem változik az összeg. Haladjunk így egyesével tovább. Amikor elérünk egy olyan területre, ahol már a \(-1\)-esek vannak „többségben”, az összeg nyilván negatív lesz, tehát valahol \(0\) is kellett legyen. Az egész hasonlít egy kicsit egy amőba mozgására, amelyik a táplálék felé mozog 😊. Csak arra kell vigyázni, hogy az „amőba” teste sose vágja ketté a maradék részt, de hát ez is megoldhatónak tűnik: az amőba a tábla szélén („fal mellett”) másszon végig, és csak akkor szakadjon el tőle, ha muszáj és ha már megfelelő pozícióban van.
Az előbb egy amőba mozgását figyeltük, Udvari Tibor megoldásában egy kígyó tekereg: A 64 beírt szám összege \(0\), a táblázatban 32 darab \(1\) és 32 darab \(-1\) van. Jelöljünk ki a táblázatban egy zárt utat, amely az összes cellán áthalad.
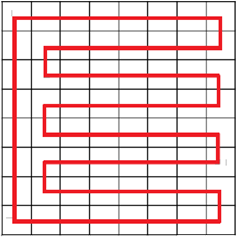
Helyezzünk erre az útra egy 32 szelvényből álló „kígyót”, amelynek minden szelvénye pontosan egy cellát fed le. Ha a kígyó által lefedett cellákon a számok összege 0, akkor készen vagyunk, a lefedett és a lefedetlen részek a tábla egy-egy összefüggő részét alkotják, mindkettőben \(0\) összeggel. Ha a lefedett számok összege nem \(0\), akkor csak páros szám lehet, mert \(n\) db 1 és \(32-n\) db \(-1\) összege \(2n-32\). A le nem fedett számok összege a feltételek szerint \(32-2n\) (mert a két rész összege \(0\)). Most mozgassuk el a kígyót a zárt úton az egyik irányba. Minden lépésben a lefedett számok összege az előző helyzethez képest vagy változatlan marad, vagy \(2\)-vel növekszik, vagy \(2\)-vel csökken. Amikor az eredetileg lefedetlen cellákat takarja a kígyó, az összeg az eredeti összeg ellentettje lesz. Menet közben tehát biztosan kellett lennie egy olyan helyzetnek, amelyben a lefedett cellák számainak összege \(0\) volt.
Ugyanez a gondolatmenet alkalmazható minden olyan téglalap alakú táblázat esetén, amelyben a táblázat oldalainak mérete páros szám. Ha páratlan szám is előfordul a méretek között, akkor vagy az egész táblázatban, vagy a két részben nem lehet \(0\) a számok összege.
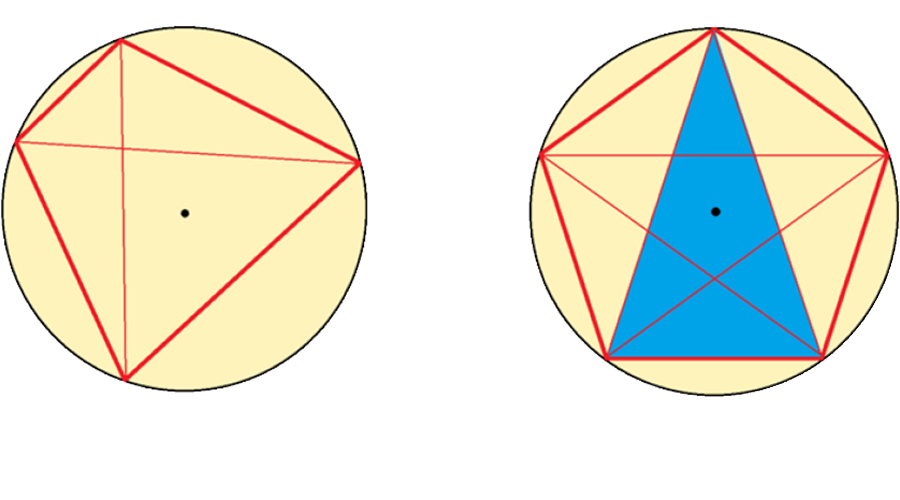
75. Legfeljebb hány pontot lehet felvenni egy körön úgy, hogy a közülük választható ponthármasok által kijelölt háromszögeknek pontosan a fele legyen hegyesszögű?
Válasz: 5.
Megoldás. Egy húrnégyszög csúcsaiból \(4\) háromszögnek a csúcsait választhatjuk ki. Egy háromszög akkor lesz hegyesszögű, ha a kör középpontja a háromszög belsejében van. A négyszöget egy átlója két háromszögre osztja, és a kör középpontja csak az egyik háromszögnek lehet belső pontja. A másik átló két újabb háromszögre osztja a négyszöget, ezekből is csak az egyik lehet hegyesszögű. Azt látjuk, hogy egy húrnégyszögben kijelölhető \(4\) háromszögből legfeljebb \(2\) háromszög hegyesszögű.
Akkor lesz a háromszögek fele, azaz \(2\) háromszög hegyesszögű, ha a kör közepe a négyszög belsejében van, és nem illeszkedik a négyszög átlóira.
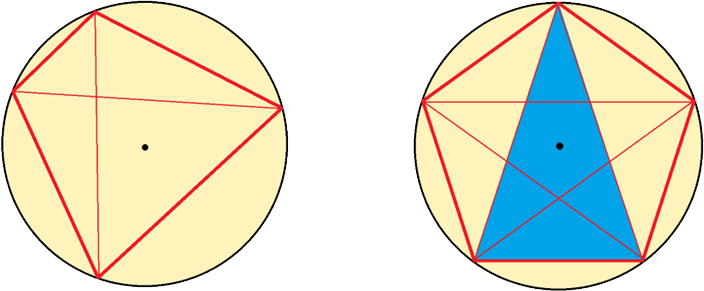
A szabályos ötszög csúcsai \(10\) háromszöget jelölnek ki, és ezeknek a fele, azaz \(5\) háromszög hegyesszögű.
\(n\) pont esetén akkor lesz a háromszögeknek pontosan a fele hegyesszögű, ha a kör közepe minden kiválasztható pontnégyesre a négyszög belsejében van, és nem illeszkedik a négyszög átlóira. Ez amiatt szükséges, mert azt láttuk, hogy egy négyszögben a \(4\) háromszögből legfeljebb \(2\) háromszög hegyesszögű, és a feltétel miatt mindig kell lennie \(2\) hegyesszögű háromszögnek.
Ha a körön \(n\geq 6\) pontot veszünk fel, akkor lesz olyan félkör, amelyen legalább \(4\) pont van. Válasszuk ki az egyik pontot, nevezzük \(A\)-nak, a rá illeszkedő átmérő két félkörre osztja a kört, és a többi legalább \(5\) pontból legalább \(3\) pont ugyanazon a félkörön van, és ők \(A\)-val egy olyan húrnégyszöget alkotnak, amelynek nem belső pontja a kör közepe. Emiatt ebben a négyszögben nincs hegyesszögű háromszög.
Emiatt \(n\geq 6\) pont esetén a háromszögek között több lesz a nem hegyesszögű, mint a hegyesszögű.
Ezek szerint legfeljebb \(5\) pontot vehetünk fel a körön.
76. Egy körre felírtuk az \(1, 2, \dots, 10\) számokat valamilyen sorrendben. Tetszőleges sorrend esetén legkevesebb hány lépésben tudjuk a tíz számot az óramutató járása szerint növekvő sorba rendezni, ha egy lépésben egy számot áthelyezhetünk a körön valamely két szám közé?
Válasz: 8.
Turchányi Gyula indoklása: A lépésszám minimalizálása ekvivalens azzal, hogy hány elemet nem kell elmozdítani. Azokat az elemeket hagyhatjuk a helyükön, amelyek már a helyes (ciklikus) relatív sorrendben vannak. Ha a kiindulási sorrend éppen fordítottja a kívántnak, akkor csak két elem maradhat a helyén, ekkor a köztük lévő mind a 8 elemet eltávolítjuk – és beszúrjuk azokat új helyükre.
77. Adott a síkon néhány pont, amelyek között nincs három egy egyenesre eső. A pontokat kiszíneztük \(4\) színnel, és mindegyik színből van legalább egy pont. Nevezzünk egy háromszöget tarkának, ha a csúcsai különböző színűek. Egy háromszög üres, ha nincs a belsejében színes pont. Van-e mindig \(3\) tarka és egyúttal üres háromszög?
Válasz: Mindig van \(3\) üres tarka háromszög.
Makay Géza megoldása: Ha egy tarka háromszögben van pont (nem üres), akkor a belső ponttal egyező színű csúcsot (vagy ha nincs ilyen, akkor bármelyik csúcsot) kicserélve a belső pontra megint csak tarka háromszöget kapunk, amelyikben kevesebb pont van, mint az eredetiben. Ezt ismételve el tudunk jutni egy olyan tarka háromszögig, amelyikben már nincs belső pont, vagyis üres. Nevezzük ezt a módszert kiürítésnek.
Ha van olyan tarka háromszög, amelyikben van egy negyedik színű pont, akkor a belső pont és a háromszög oldalai által megadott háromszögek is tarkák, azokat kiürítve kapunk három különböző üres és tarka háromszöget.
Ha az előbbi feltevés nem teljesül, akkor bármelyik \(4\) különböző színű pont konvex burka négyszög kell legyen. Jelöljük a csúcsokat a négyszög óramutató járásával egyező irányú körbejárása szerint \(A\), \(B\), \(C\) és \(D\) betűkkel és a pontokon használt színeket ugyanazokkal a kis betűkkel. Vegyük ebből a négyszögből az \(ABC\), \(ABD\) és \(ACD\) tarka háromszögeket, és ürítsük ki őket. Kapunk három üres és tarka, de nem feltétlenül különböző háromszöget.
Mégis állítom, hogy az így kapott háromszögek különbözőek. Legyen az átlók metszéspontja \(P\). A feltevés szerint az \(ABC\) háromszögben nincs \(d\) színű pont, az \(ABD\)-ben pedig nincs \(c\) színű pont. Ha ezen két háromszög kiürítésekor kapott háromszög ugyanaz lenne, akkor annak az \(ABP\) háromszögben kellene lennie, de azon belül csak kétféle szín fordulhat elő (\(a\) és \(b\)), így az nem lenne tarka. Ugyanígy belátható, hogy az \(ABC\) és \(ACD\) kiürítésekor, illetve az \(ABD\) és \(ACD\) kiürítésekor is más-más üres és tarka háromszöget kapunk, így megint találtunk három különböző üres és tarka háromszöget.
Udvari Tibor megoldása: A \(4\) szín legyen piros \((P)\), kék \((K)\), zöld \((Z)\) és sárga \((S)\). Ezek mindegyike előfordul, így található \(4\), különböző színezésű tarka háromszög.
Megmutatjuk, hogy valamely három színt választva egy tarka háromszögből vagy van egy üres, vagy van a másik háromféléből egy-egy üres.
Keressünk például egy \(PKZ\) tarka háromszöget. Ilyen biztosan van, mert mindhárom színű pontból van legalább egy és semelyik három pont nincs egy egyenesen. Ez a háromszög vagy üres (találtunk egy üres, \(PKZ\) színezésű tarka háromszöget), vagy vannak benne pontok. Ha vannak benne pontok, és van közöttük a \(P\), \(K\), \(Z\) színek valamelyike, például \(Z\), akkor az eredetileg választott \(Z\) pontot erre kicserélve, egy kisebb, új \(PKZ\) tarka háromszöget kapunk. A három színből véges sok pontunk van, ezért az eljárást ismételgetve előbb-utóbb olyan \(PKZ\) háromszöghöz jutunk, amely vagy üres (találtunk egy üres, \(PKZ\) színezésű tarka háromszöget), vagy csak \(S\) színű pontok vannak benne. Ez utóbbi esetben lesz három tarka és üres háromszögünk. Ehhez csak össze kell kötni az oldalak végpontjait az oldalhoz legközelebbi sárga ponttal. Tehát vagy kapunk egy \(PKZ\) tarka és üres háromszöget, vagy kapunk három, \(PKS\), \(PZS\) és \(ZKS\) tarka és üres háromszöget.
Ugyanez a gondolatmenet \(PKS\), \(PZS\) és \(ZKS\) színű kiinduló háromszögekkel is elvégezhető. Ha bármikor kapunk három tarka és üres háromszöget, akkor készen vagyunk. Ha nem kapunk ilyet egyik esetben sem, akkor van négy tarka és üres háromszögünk.
Négy pont esetén mind a két eset előfordulását mutatja a két alábbi ábra:
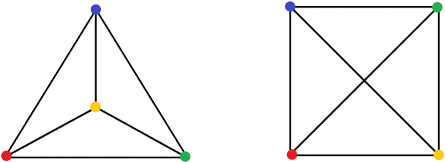
Dombi Péter megoldása: Válasszuk ki azt az \({A,B,C,D}\) négyszínű pontnégyest, aminek a konvex burka a legkisebb területű. Jelöljük a konvex burkot \(P\)-vel.
\(\bullet\) Ha \(P\) négyszög, akkor biztosan üres, mert ha \(X\) egy színezett belső pont, és az \(X\) pont színét \(c(X)\)-szel jelölve például \(c(X)=c(A)\) lenne, akkor az \(XBCD\) négyszínű négyes konvex burka \(P\)-nél kisebb területű lenne. Ezért ilyenkor legalább \(4\) tarka üres háromszög van: \(ABC\), \(ABD\), \(ACD\), \(BCD\).
\(\bullet\) Ha \(P\) háromszög, az \(A\), \(B\), \(C\) csúcsokkal, akkor \(D\) ennek egy belső pontja. Az \(ABC\) háromszögben lehetnek más színezett pontok is, de azok biztosan \(D\)-vel azonos színűek, mert ha például \(A’\) egy \(A\)-val azonos színű belső pont lenne, akkor \(A’BCD\) konvex burka a háromszög belsejébe esne, ami ellentmondana az \(ABCD\) választásának. Tehát \(ABC\)-ben csak \(D\)-vel azonos színű pontok vannak. Legyen \(D_a\), \(D_b\), \(D_c\), rendre az \(BC\), \(AC\), \(AB\) oldalhoz legközelebbi – nem feltétlen különböző – színes belső pont. Ekkor a \(D_a BC\), \(D_b CA\) és \(D_c AB\) háromszögek tarkák és üresek, azaz ilyenkor is található \(3\) megfelelő háromszög.
Róka Sándor