A Monty Hall-paradoxont, amely a nevét egy amerikai vetélkedő („Let’s Make a Deal”, Magyarországon „Zsákbamacska” címen volt látható) műsorvezetőjéről kapta, sokan ismerhetik:
Egy tévés vetélkedő korai változatának a végén a játékosnak mutattak három ajtót, közülük az egyik mögött volt a nyeremény, a másik kettő üres. Ő választ egyet az ajtók közül, majd, hogy egy kis csavar legyen a dologban, a műsorvezető (Monty Hall), kinyit egy ajtót a maradék kettő közül, amely mögött nincsen semmi. Ekkor a játékos, ha szeretné, még megváltoztathatja a választását a két csukott ajtó közül a másikra. A kérdés, hogy érdemes-e változtatnia?
Amikor elmagyarázzák, hogy igenis érdemes váltani, mert ezzel megduplázza a nyerési esélyét, sokan úgy érzik, hogy ebben van valami csalás, valami, amit elhallgatnak előle. Mi lehet emögött?
Németh Hanna1 a videójában feldob két pénzérmét, megnézi őket, majd elárulja, hogy az egyik fej. Amikor ezután levezeti, hogy ekkor a másik érme kétszer akkora valószínűséggel lesz írás, mint fej, az sokakban ösztönös tiltakozást vált ki. Mintha valami fontos dolog hiányozna még az érvelésből. De vajon mi?
A cikk első részében ezekkel a kérdésekkel foglalkozunk, elsősorban egy olyan szempontból, amely a szokásos tárgyalásokból gyakran kimarad: mi az információ közlésének a módja, kontextusa? Erre fókuszálva a fenti problémák különböző változatait egységes keretben tárgyaljuk. Ezt az átfogó elemzést ajánljuk azoknak is, akik most találkoznak először ezekkel a paradoxonokkal.2 A cikkhez tartozó Függelékben közöljük a főszövegbeli ábrákhoz tartozó formális levezetéseket, számolásokat.
A második részben pedig az első példáit továbbgondolva egy általánosabb valószínűségszámítási vizsgálatra hívjuk azokat az olvasóinkat, akik az említett paradoxonokat már jól ismerik (például az első részből).
Ha többlet infomációhoz jutunk, akkor az mindig segít-e? Vagy ha valakitől hallunk egy bizonytalan jelenség körülményeiről – még ha igazat mond is – akkor ez mindig közelebb visz-e megismeréshez, megértéshez?
Konkrétan, ha tudunk valamit egy kísérlet kimeneteléről, akkor az már automatikusan feltételes valószínűség?
Pontosabban: ha tudjuk, hogy a \(B\) esemény bekövetkezett, akkor innentől egy \(A\) esemény valószínűsége \(P(A \mid B)\) lesz?3
Még pontosabban: ha valaki közöl velünk valamit egy kísérlet kimeneteléről, mondjuk azt, hogy a \(B\) esemény bekövetkezett, akkor egy \(A\) esemény valószínűsége \(P(A \mid B)\) lesz?
A válaszunk az, hogy nem. Hanem számít az is – sőt, meghatározó –, hogy milyen kontextusban közli! Ezt a jelenséget a fenti paradoxonok segítségével illusztráljuk, majd az ilyen szituációk kezelésére bevezetünk egy egyszerű modellt, amit közlési protokollnak nevezünk. A közlési protokoll alapján tudunk feltételeket mondani arra, hogy az \(A\) esemény valószínűsége a \(B\) bekövetkezésének ismeretében megegyezik-e a \(P(A \mid B) \) feltételes valószínűséggel vagy sem. Úgymond, hogyan torzít a közlési protokoll.
A cikkekben bemutatott gondolatok tanulsága az, hogy az egyik legfontosabb információt gyakran nem hangsúlyozzák ki, néha pedig meg sem említik a fentiekhez hasonló feladatok megfogalmazása során. Ezért a valószínűségi paradoxonok befogadásával szembeni ellenállásnak matematikai létjogosultsága is van, az nem csak pszichológiai jellegű, nem csak arról szól, hogy az emberek hajlamosak rosszul megbecsülni a valószínűségeket. A megfelelő modell felállítása gyakran nem következik a feladatok megfogalmazásából, és más értelmezésekhez más modellek, és így más megoldások tartoznak.
1. Monty Hall-probléma
Monty Hall első (eredeti) változat: Egy tévés vetélkedő végén a játékosnak mutatnak három ajtót, közülük az egyik mögött van a nyeremény, a másik kettő üres. Ő választ egyet az ajtók közül, majd, hogy egy kis csavar legyen a dologban, a műsorvezető (Monty Hall), aki tudja, melyik ajtó mögött van a nyeremény, kinyit egy olyan ajtót a maradék kettő közül, amely mögött nincsen semmi. Ekkor a játékos, ha szeretné, még megváltoztathatja a választását a két csukott ajtó közül a másikra. A kérdés, hogy érdemes-e változtatnia?
A fejtörő megfejtése: igen, érdemes. Ugyanis – a rövid indoklás szerint – eredetileg \(1/3 \approx 33{,}3\%\) valószínűséggel találta el a játékos a nyereményt, amely tehát \(2/3 \approx 66{,}6\%\) valószínűséggel a másik két ajtó közül valamelyik mögött van. Ezen a valószínűségen nem változtat az, hogy kinyitnak egy olyan ajtót, amely mögött nincsen semmi, így a játékos által nem választott most már egyetlen ajtó örökli meg ezt a \(66{,}6\%\)-ot. Tehát ha a játékos megváltoztatja a tippjét, azzal kétszeresére növeli a nyerés esélyét. Részletesebb levezetés a Bayes-tétel alapján megtalálható például a Matekingen, de ebben a cikkben is vissza fogunk térni rá, lásd a 8. ábrát.
Kísérletileg is kipróbálhatjuk párban három lefordított pohárral, egyik alatt a nyeremény. Ha egy papíron vezetjük az eredményt, kiderül, hogy kb. az esetek \(2/3\) részében fog nyerni a játékos, ha mindig vált, és kb. az esetek \(1/3\) részében nyer, ha nem vált.
Mi ebben a meglepő? Mit várnánk e helyett? Persze, ki mit. Én azt várnám, hogy mindegy, hogy váltunk-e, 50–50% a két csukva maradt ajtó valószínűsége. Miért várom ezt? Azért, mert ha csak azt látnám, hogy egyik ajtó (mondjuk, \(C\)) nyitva van és üres, akkor a két másik ajtó (\(A\) és \(B\)) valószínűsége egyenlő, lásd az 1. ábrát. Ez éppen a feltételes valószínűség: mennyi a valószínűsége, hogy a nyeremény az \(A\) ajtó mögött van, ha nincs a \(C\) ajtó mögött?
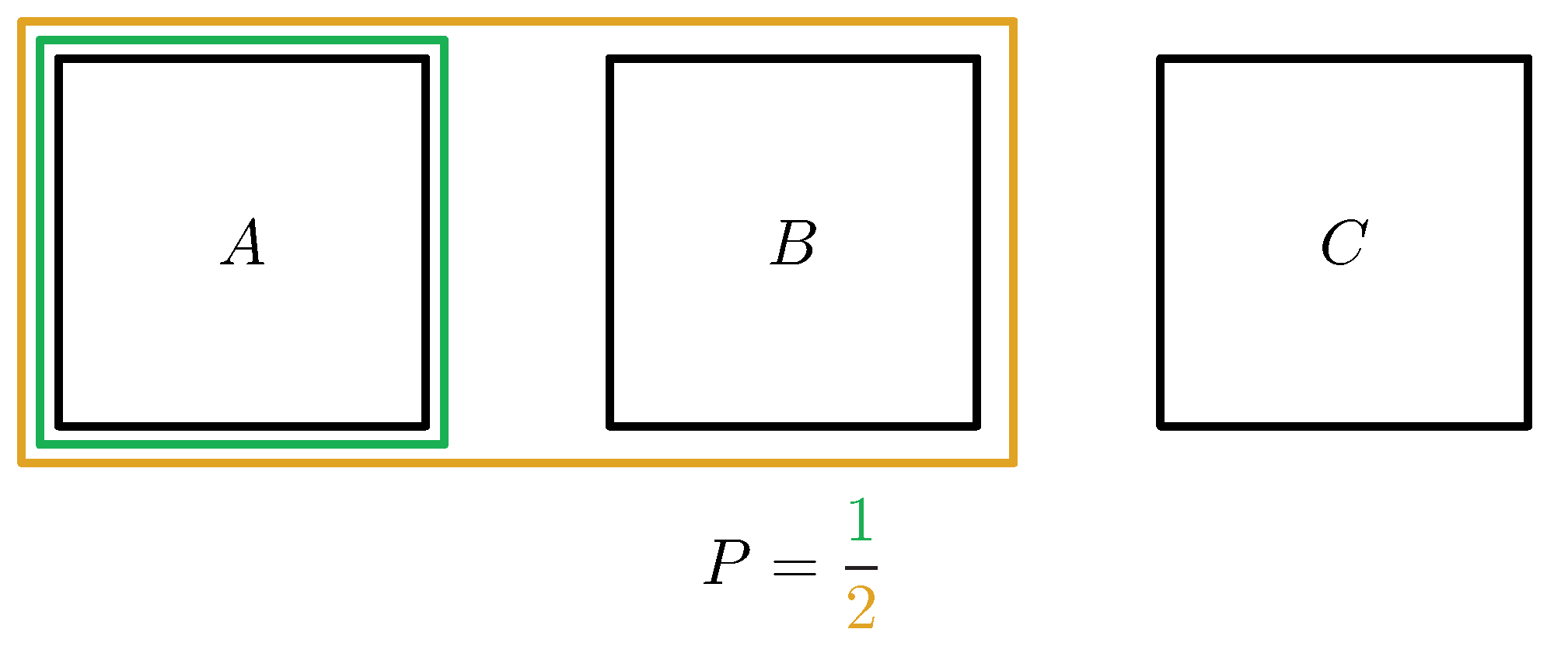
Így tekintve tehát a megoldás éppen a bevezetőben feltett kérdés alapján mond ellent a szemléletünknek (ezért „paradoxon”): Tudjuk, hogy a nyeremény nincs a \(C\) ajtó mögött, mégsem az ezzel a feltétellel vett feltételes valószínűség adja meg a helyes választ. Számít az, hogy honnan tudjuk, hogy nincs a \(C\) ajtó mögött nyeremény, azaz számít, hogy a közlő (aki ez esetben a játékvezető) milyen kontextusban közölte azt!
Még meglepőbb azonban, hogy ha egy kicsit módosítjuk a feladatot, más lesz a megoldás:
Monty Hall második (módosított) változat. Egy tévés vetélkedő végén a játékosnak mutatnak három ajtót, közülük az egyik mögött van a nyeremény, a másik kettő üres. Ő választ egyet az ajtók közül, majd, hogy egy kis csavar legyen a dologban, a műsorvezető (Monty Hall) kinyit egy ajtót a maradék kettő közül, és kiderül, hogy nincs mögötte semmi. Ekkor a játékos, ha szeretné, még megváltoztathatja a választását a két csukott ajtó közül a másikra. A kérdés, hogy érdemes-e változtatnia?
Mi a különbség az első verzióhoz képest? Az, hogy itt a műsorvezető véletlenszerűen nyit ki egy ajtót a maradék kettő közül (amiket nem választott a játékos), kockáztatva ezzel, hogy véletlenül azt nyitja ki, amely mögött a nyeremény van (ha a játékos nem azt választotta). De a szöveg szerint szerencséje van, és pont egy üres ajtót sikerül kinyitnia. Ezzel szemben az első változatban szándékosan egy üres ajtót nyit ki azok közül, amiket nem választott a játékos – nem bízza a véletlenre.
A végső állapot, amit látunk, mindkét változatban ugyanaz: a három ajtó közül az egyik nyitva áll és üres, és a játékosnak a másik két ajtó közül kell választania. Sőt, nemcsak a végső állapot ugyanaz, hanem a játékos szemszögéből az egész folyamat is ugyanaz: a játékvezető kinyit egyet a maradék két ajtó közül, és az üres.
A második verzióban a két csukott ajtó (\(A\) és \(B\)) valószínűsége 50–50%, azaz nem öröklődik át a ki nem választott \(B\) és \(C\) ajtókra vonatkozó \(66{,}6\% \) nyerési valószínűség a ki nem választott és csukva maradt \(B\) ajtóra. Ezt később levezetjük az első verzióhoz hasonlóan (lásd a 9. ábrát), de addig is ki lehet próbálni párban kísérletezve. Ha a játékvezető véletlenül olyan ajtót nyit ki, amely mögött a nyeremény van, azt ne vegyük figyelembe a kísérlet során. Azon kimenetelek esetén, amikor üres ajtót sikerült kinyitnia, az esetek kb. felében nyer a játékos, akár változtat, akár nem.
Vajon azért kapunk a második változatban éppen 50%-ot, amely megegyezik a feltételes valószínűséggel („az \(A\) ajtó mögött van a nyeremény, feltéve, hogy nincs a \(C\) mögött”), mert a játékvezető is véletlenszerűen választott? Ez lehet a kulcs? Nem, ez inkább egy véletlen egybeesés, amint a cikk második részében látni fogjuk.
Mi van, ha nem tudjuk, hogy mi alapján választotta ki az ajtót a játékvezető? A cikk bevezetőjében szándékosan egy ilyen verziót közöltünk: pontatlanul fogalmaztuk meg a Monty Hall-problémát, lebegtetve hagytuk, hogy melyik változatról van szó. Ilyenkor nem lehet megállapítani a valószínűséget. Azonban játékelméleti eszközökkel lehet további megállapításokat tenni ilyen esetben is, amint arra Konczer József rámutatott.
2. Van fej
Németh Hanna egy hasonló, szemléletünknek ellentmondó jelenséget mutatott be az említett videóban. Feldob két pénzérmét, megnézi őket, majd közli: „Elárulom nektek, hogy az egyik fej.” Mennyi a valószínűsége, hogy a másik is fej?
Hanna érvelése szerint a négyféle kimenetelből (\(FF\), \(IF\), \(FI\), \(II\)) három esetben teljesül, hogy az egyik fej (\(FF\), \(IF\), \(FI\)), és ezek közül egy esetben a másik is fej (\(FF\)). Tehát a valószínűség \(1/3\), lásd a 2. ábrát. Ez éppen a feltételes valószínűség: mennyi a valószínűsége, hogy mindkettő fej, ha legalább az egyik fej? [2]
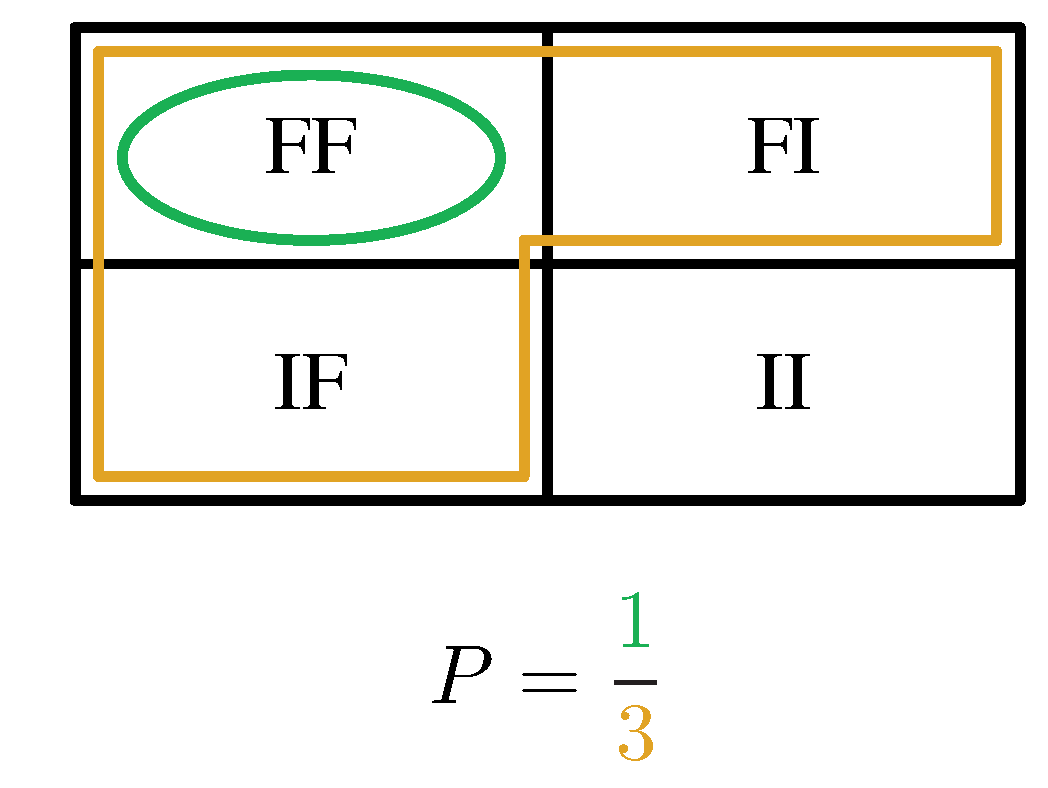
Tiszta ügy. Vagy mégsem? Mi lehet ezzel a probléma? Az, hogy nem tudjuk, hogy Hanna hogyan döntötte el, hogy a fejet fogja közölni és nem az írást. Ugyanis \(FI\) és \(IF\) esetén azt is mondhatná, hogy „Elárulom nektek, hogy az egyik írás.” Szőrszálhasogatásnak tűnik, ugye? De a Monty Hall két verziója után már sejthetjük, hogy valójában minden ezen múlik. Milyen módszerekkel dönthette el Hanna, hogy a fejet vagy az írást közli a vegyes esetekben? Nevezzük ezt a módszert, kontextust mostantól közlési protokollnak. Például:
(1) \(FF\) esetén fejet mond, \(II\) esetén írást mond, \(FI\), illetve \(IF\) esetekben pedig véletlenszerűen dönti el, hogy fejet vagy írást mond.
(2) Az első pénzérme eredményét közli (ilyenkor feltesszük, hogy a két érmét meg tudja különböztetni, például az egyik százas a másik pedig kétszázas).
(3) A kettő közül kiválaszt egyet, és annak az eredményét közli.
(4) Előre elhatározza, hogy a fejre fog koncentrálni, így \(FF\), \(IF\) és \(FI\) esetén közli, hogy „az egyik fej”, \(II\) esetén meg azt mondja, hogy „nincs fej”, vagy esetleg azt, hogy „az egyik írás”.
(5) Valaki megkérdezi, hogy van-e köztük fej, és erre válaszol.
(6) Előre elhatározza, hogy a fejre fog koncentrálni, így \(FF\), \(IF\) és \(FI\) esetén bemondja, hogy „az egyik fej”, \(II\) esetén pedig újraveszi a videót (illetve újra dob, és levágja a videó elejét).
Persze az (5)-ös protokoll nem lehetett, mert nem hallottunk kérdést a videóban, tehát ezt a lehetőséget én költöttem hozzá, mindjárt kiderül, hogy miért.
Ha valaki ilyen videót szeretne készíteni, akkor az (1)–(3) protokollok használata kézenfekvőnek tűnik. Azonban így a kérdéses valószínűség nem \(1/3\) lesz, hanem \(1/2\). Miért?
Az (1) szerint \(FI\), illetve \(IF\) esetén fele akkora valószínűséggel fogja a fejet közölni, mint \(FF\) esetén, így ha fejet közöl, akkor 50% valószínűséggel \(FF\) a kimenetel (és 25% valószínűséggel \(FI\), illetve \(IF\)). Lásd a 3. ábra bal oldali részét és az 5. ábrát.
A (2) szerint \(IF\) esetén nem a fejet közölné, hanem az írást. Így „az egyik fej” közlés csak \(FI\) és \(FF\) esetén hangozhat el, tehát az \(FF\) valószínűsége megintcsak 50%. Lásd a 3. ábra jobb oldali részét és a 6. ábrát.

A (3) protokoll lényegében ugyanaz, mint az (1)-es, ha véletlenszerűen választ, hiszen ekkor \(FI\), illetve \(IF\) esetén 50–50% valószínűséggel mondja, hogy „van fej”.
A (4) protokoll az, amivel működne Hanna érvelése, miszerint a \(FF\) valószínűsége \(1/3\), lásd a 2. és a 7. ábrát. Csak ennek a protokollnak a gyakorlati megvalósításával van némi probléma. Ha előre elhatározta, hogy a fejre fog koncentrálni, azt a nézőnek is tudni kellene, e nélkül ugyanis nem helyes a számolás, az \(FF\) valósznűsége nem \(1/3\) lesz. Ez tehát egy extra információ, amit hozzá kell tenni, ha így szeretnénk számolni. A videó semmilyen módon nem utal arra, hogy ezt a protokollt használná.
A (4) protokoll megtöri a fej és írás szimmetriáját, méghozzá a fej javára. Nevezzük ezt fejdomináns protokollnak. Ha éppen ellenkezőleg, azt határozta volna el előre a közlő, hogy az írásra fog koncentrálni, tehát \(IF\), illetve \(FI\) esetén írást mond (írásdomináns protokoll), akkor a „van fej” csak \(FF\) esetén hangozhat el, így ilyenkor az \(FF\) valószínűsége 1 lenne. Hanna videójában akár ez is lehetne a helyes megoldás, hiszen nem derül ki, mi a protokoll. Pontosabban, eddig egy olyan protokollt találtunk, a fejdominánsat, ami a videóban bemutatott eredményre vezet, de ezzel az erővel a valójában alkalmazott protokoll lehetne az írásdomináns is. (Hanna saját bevallása szerint a legkézenfekvőbb (1) protokoll szerint járt el.)
Az (5) protokoll természetes módon megoldaná a szimmetriatörést, mert a közlő a kérdésre válaszolna. Ez tehát egy életszerű megoldás lenne arra, hogy tudassuk a nézővel, hogy a fejdomináns protokollt alkalmazzuk. (És akkor \(FF\) valószínűsége \(1/3\) lenne, hiszen ez igazából a (4)-es protokoll.)
Azonban a (4) és (5) protokollokkal a közlő azt kockáztatja, hogy nem lesz fej a dobások között, így nem közölheti azt, hogy „az egyik fej”. Ezt a problémát látszólag megoldaná a (6) protokoll a videóvágással, de valójában nem, hiszen ez attól még ugyanúgy a (4)-es protokoll.
Abban a zavarba ejtő helyzetben vagyunk, hogy bár a „másik is fej, ha az egyik fej” feltételes valószínűség \(P(FF \mid A)=1/3\), nem tudjuk ezt természetes módon megjeleníteni egyetlen érmedobással. Ez persze összhangban van azzal, hogy a valószínűség egy kísérletsorozatról mond valamit: a valószínűség kb. megegyezik a relatív gyakorisággal a nagy számok törvénye szerint. Százszor feldobva a két pénzérmét, válogassuk ki azokat a kimeneteleket, amikor „az egyik fej”, ezeknek kb. \(1/3\)-ában a másik is fej lesz. Ha mégsem így lenne, akkor dobjuk fel a két érmét ezerszer. Ez volna egy konkrét és helyes megjelenítése a videóban bemutatni szándékozott valószínűségnek.
3. Van két gyerekem, az egyik lány
Egy közismert átfogalmazása az előbbi feladatnak a fiú–lány paradoxon, lásd például ezt és ezt a videót. Egy apa közli: „Van két gyerekem, az egyik lány…” Mennyi a valószínűsége, hogy a másik is lány? A leggyakrabban bemutatott megoldás megegyezik a két pénzérméssel: a két gyerek fiú–lány, lány–fiú vagy lány–lány lehet, ebből egy esetben lány a másik gyerek is, tehát a valószínűség \(1/3 \approx 33{,}3\%\).
Az értetlenkedőkben és tiltakozókban valami ilyesmi kérdés lappanghat: nem lehet, hogy a kétlányos apáktól gyakrabban hangzik el ez a mondat: „Van két gyerekem, az egyik lány…”? Hiszen akiknek egyik gyereke lány, a másik meg fiú, ők néha azt mondják, hogy „… az egyik fiú…”. Matematikai szemmel nézve elsőre nagyon amatőrnek tűnhet ez a kifogás, pedig valójában ezen múlik minden: milyen kontextusban (milyen körülmények között, milyen céllal) közölte az apa ezt az információt a gyerekeiről? Néhány lehetséges közlési protokoll:
(1) Ha egy fia és egy lánya van, véletlenszerűen dönti el, melyiket említse meg.
(2) A kisebbik gyerekének a nemét közli.
(3) A nappalijukban mesél: „Van két gyerekem…”, és ekkor kiszalad az egyik gyerek a kisszobából, történetesen egy lány.
(4) Előre elhatározza, hogy a lányt fogja mondani.
(5) Valaki megkérdezi, hogy van-e köztük lány, és ő erre válaszol.
(6) A mondata így folytatódik: „Van két gyerekem, az egyik lány, és Annának hívják.”
(6′) A mondata így folytatódik: „Van két gyerekem, az egyik lány, és január első felében született.”
(7) A mondata így folytatódik: „Van két gyerekem, az egyik lány, és hétfőn született.”
(8) A mondata így folytatódik: „Van két gyerekem, az egyik lány, és délután (dél és éjfél között) született.”
Az (1)–(5) protokollok megfelelnek a két pénzérmés feladat (1)–(5) protokolljainak. Valóban, (1) az, hogy vegyes esetben véletlenszerűen választunk, (2) az, hogy az első érmét mondjuk, (3) az, hogy az egyiket megnézzük, és azt mondjuk. Ilyenkor tehát a lány–lány valószínűsége 50%, nagyon is helyt adva ezzel a tiltakozásnak. A (4) a lánydomináns protokoll, ez vezet a „mindkettő lány, ha egyik lány” feltételes valószínűségre, ami \(\approx 33{,}3\%\). Az (5)-ös protokoll teszi életszerűvé a (4)-est a kérdés által.
És ne feledjük, a valószínűség csak sokszor megismételt kísérletről mond valamit a nagy számok törvénye szerint. Ha a Kétgyerekes Apák Napján a Hősök terén összegyűlt többezer kétgyerekes apát megkérjük hangosbemondón, hogy álljon a tér bal felére, akinek az egyik gyereke lány, akkor kb. a \(3/4=75\%\)-uk áll oda. Most megkérdezzük, hogy kiknek lány a másik gyereke is, akkor a tér bal oldalán állók kb. \(1/3 \approx 33{,}3\%\)-a fogja feltenni a kezét, azaz az összes kétgyerekes apák 25%-a.
A (6)–(8) protokolloknál az apa kiegészíti a közlését egy olyan információval, amely teljesen irrelevánsnak tűnik abból a szempontból, hogy a másik gyerek is lány-e. Nem látszik, mi volna ezeknek a megfelelője a kétérmés megfogalmazásban. Mivel a fiú–lány paradoxonnal kapcsolatos videók és írások ilyen extra információkkal kiegészített közlésekkel szokták folytatni a meglepetések sorozatát, nem térhetünk ki az elől, hogy e cikkben is szót ejtsünk róluk. Azonban ki fog derülni, hogy ezek kicsit más jellegű bonyodalmakat okoznak, mint az eddig tárgyalt közlések, ezért itt csak éppen kitérünk rá. [3] Ezt a kitérőt is bátran ugorja át az, aki a Monty Hallal és a két pénzérmés feladattal kapcsolatban felvetetett problémák tárgyalását szeretné folytatni a következő fejezetben!
Nézzük, mi történik a (6)-os közlésnél. Tegyük fel, hogy a lányok 4%-át hívják Annának (bármi más (kis) számot is mondhatnék, nem függ ettől az érvelés, sem az eredmény). Mi történik, ha a téren összegyűlt kétgyerekes apákat megkérdezzük, kinek van Anna nevű gyereke? Akinek nincs lánygyereke, az nyilván nem jelentkezik. A lány–fiú vagy fiú–lány gyerekekkel rendelkező apák körülbelül 4%-ának hívják az egyetlen lányát Annának. A kétlányos apák körében viszont már a 8%-uknál Anna az egyik lány. Ezért ha azt halljuk, hogy az egyik gyerek lány és Anna, akkor 50% valószínűséggel mindkét gyerek lány. Ebben az érvelésben néhány részletet jótékonyan elhallgattam, hogy ne vesszünk el bennük. [3]
A (6′), (7), (8) közlések egészen hasonlónak tűnnek a (6)-hoz. Január első felében a gyerekek \(\approx 4\%\)-a születik, hétfőn az \(1/7 \) részük, délután az 50%-uk. Ehhez persze fel kell tennünk, hogy a gyerekek egyenletesen születnek (az időintervallum hosszával arányosan), ami nem feltétlenül jogos feltevés.4 Feltesszük azt is – szintén vitatható, hogy mennyire jogosan –, hogy a gyerekek születési ideje egymástól független. [3]
Ezekkel a feltevésekkel tehát van egy \(p\) gyakoriságú tulajdonság (hogy mikor született), amely tehát a gyerekek \(p\)-szeresére igaz. A (6′), (7), illetve (8) esetekben rendre \(p=0{,}04=4\%\), \(p=1/7\), illetve \(p=1/2\). Minden egyes gyerek esetén \(p\) a valószínűsége, hogy rá igaz ez a tulajdonság, egymástól függetlenül. Jelölje \(\mathcal{F}\) azt, hogy egy gyerek fiú, \(\mathcal{L}_a\) azt, hogy lány és teljesül rá ez a tulajdonság, \(\mathcal{L}_n\) pedig azt, hogy lány, és nem teljesül.
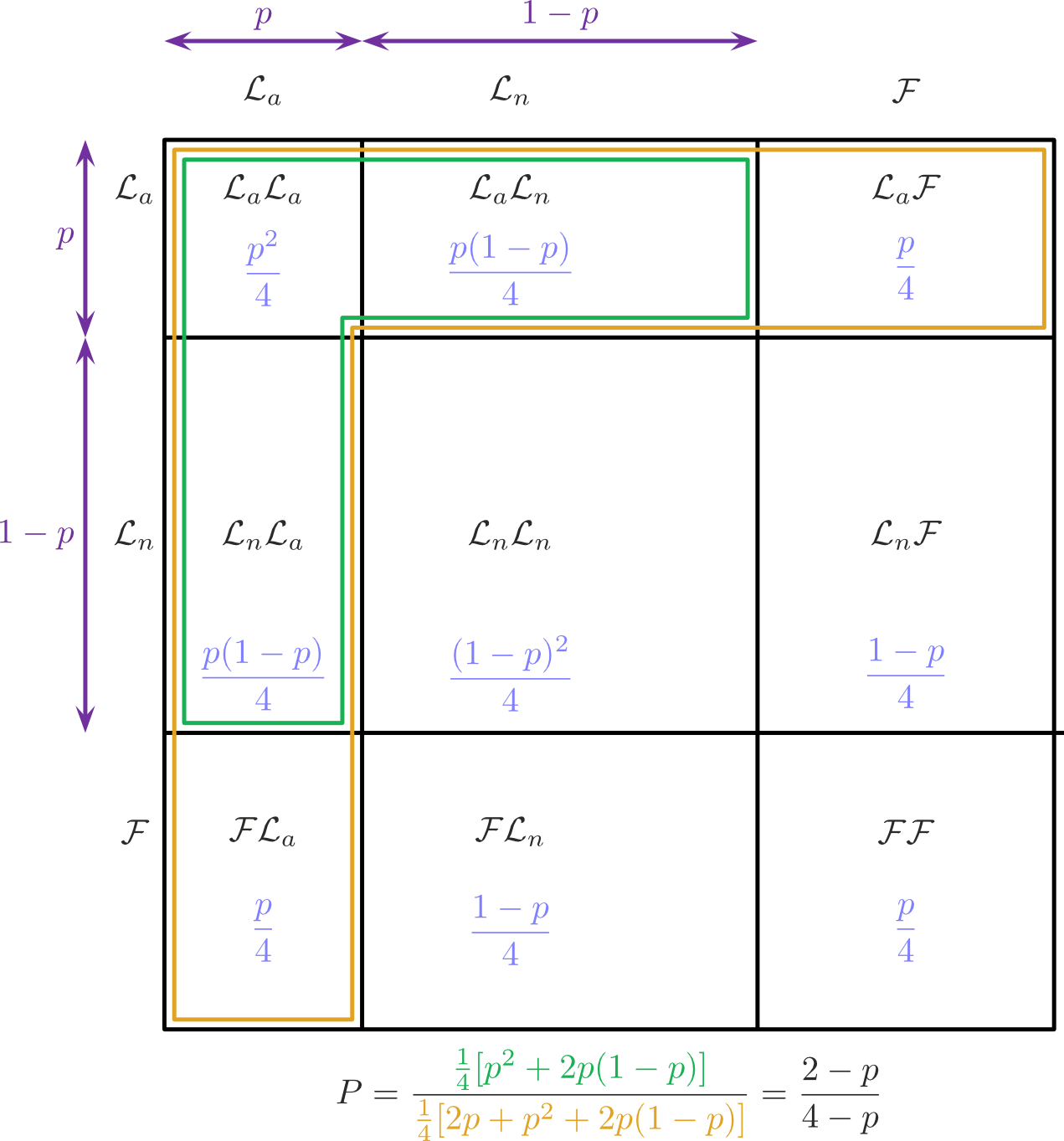
A 4. ábrán láthatjuk az egyes esetek valószínűségeit. A függetelenség miatt a két gyerek valószínűségeit össze kell szoroznunk, így pélául az \(\mathcal{F} \mathcal{L}_a\) valószínűsége \((1/2) \cdot (p/2)=p/4\), az \(\mathcal{L}_a \mathcal{L}_n\) valószínűsége \((p/2) \cdot (1-p)/2=p(1-p)/4\), és így tovább. Az ábra alapján, ha az egyik gyerek lány, és teljesül rá az extra tulajdonság (január első felében, hétfőn, illetve délután született), akkor annak a valószínűsége, hogy a másik is lány, [3]
| \(\displaystyle P=\frac{2-p}{4-p}.\) | \((1)\) |
Ha \(p\) kicsi, például \(p=0{,}04\) ((6′): lány és január első felében született), akkor ez a valószínűség kb. \(P \approx 1/2=50\%\), ennyi tehát a valószínűsége, hogy a másik gyerek is lány. Hétfőn születés ((7)-es) esetén \(p=1/7\), így \(P=13/27\), amely körülbelül 48%. A (8) protokollnál (dél és éjfél között született) \(p=1/2\), így \(P=3/7=42{,}8\%\) annak a valószínűsége, hogy a másik gyerek is lány.
| \(p:\) | \(0\) | \(0{,}04\) | \(0{,}142\) | \(0{,}5\) | \(1\) |
| \(P:\) | \(0{,}5\) | \(0{,}495\) | \(0{,}481\) | \(0{,}428\) | \(0{,}333\) |
Minél nagyobb valószínűségű eseményt közöl az apa (azaz \(p\) minél közelebb van 1-hez), annál közelebb lesz a \(P\) valószínűség \(1/3\)-hoz. Ha semmi extrát nem közöl az apa, esetleg csak elismétli, hogy az egyik lány, akkor \(p=1\), és így \(P=1/3\) annak a valószínűsége, hogy a másik gyerek is lány. Ilyen közlésekkel tehát megvalósíthatunk egy folytonos átmenetet \(P=1/2\) és \(P=1/3\) között.
Visszatérve a (6)-ra, ott is egy \(p=0{,}04=4\%\) gyakoriságú tulajdonságot közöl az apa, akárcsak (6′) esetén. Mi a különbség a kétféle közlés között? Az egyik különbség, hogy míg Annának hívni csak lányokat szoktak, január első felében fiúk is születnek. De ez nem okoz semmilyen különbséget a (6)-hoz képest. Szerintem ez is meglepő, hiszen azt gondolnám, hogy ha valaminek köze van ahhoz, hogy a másik gyerek is lány-e, akkor az az extra közlemény lányspecifikus jellege. Ez mégsem számít, hiszen a fiúk \(F\) csoportját nem kell kettészednünk az extra tulajdonság szerint.
A másik különbség, hogy egy testvérpár mindkét tagja születhet január első felében, míg Annának legfeljebb egyiküket hívhatják. Ezt az eltérést különböző források különbözőképpen kezelik. Például Keszthelyi Gabriella: Milyen színű a valószínű? című könyvében (97. oldal) úgymond elhanyagolja ezt a különbséget, és függetlennek tekinti a névadást testvérpárok esetén is. Így egy nagyon pici, a mi számadatainkkal \(0{,}4 \cdot 0{,}4=0{,}0016\), azaz \(1{,}6\) ezrelék valószínűséggel egy testvérpár mindkét tagját Annának hívják (előfordult már ilyen), és a (6′)-vel megegyező módon \(\approx 50\%\) lesz valószínűsége annak, hogy a másik gyerek is lány, ha az egyik lány, és Annának hívják. Ilyenkor fontos az, hogy \(p\) kicsi legyen.
A fejezet elején hivatkozott videók más megoldást választanak. Felteszik, hogy a lány–lány testvérpárok körében pontosan az a lánynéveloszlás, mint a fiú–lány, illetve lány–fiú pároknál, azzal a plusz megkötéssel, hogy nem kaphat két testvér ugyanolyan nevet. Ekkor pontosan 50%-ra jön ki annak a valószínűsége, hogy a másik gyerek is lány, ha az egyik lány, és Annának hívják. Ebben a verzióban nem kell \(p\)-nek (azaz az Anna név gyakoriságának) kicsinek lenni, tetszőleges \(p<1/2\) esetén működik az érvelés. [3]
4. Közlési protokollok
A felvetett kérdések okozta zűrzavar kezelésére bevezetünk egy egyszerű modellt, amit közlési protokollnak nevezünk.
Igazából két véletlen történésről van szó: először történik egy kísérlet, majd pedig egy közlés a kísérlet a kimeneteléről. A kísérlet kimeneteleinek halmaza egy \(X\) eseménytér. Tegyük fel az egyszerűség kedvéért, hogy \(X\) véges halmaz. Például a kétérmés feladatban \(X=\{FF, FI, IF, II\}\).
Majd a közlés során a közlő elárul valamit a kimenetelről, vagyis közli, hogy egy \(B \subset X\) esemény bekövetkezett. Így a másik eseménytér, az \(Y\) közléstér elemei az \(X\) részhalmazainak (azaz eseményeinek) felelnek meg. Legyen \(y_B \in Y\) az a kimenetel, hogy a közlő a \(B \subset X\) esemény bekövetkezését közli. Persze a példákban csak néhány eseményt fog pozitív valószínűséggel közölni a közlő, de elvileg bármilyen \(X\)-hez tartozó eseményt közölhetne.
1. példa. Nézzük először a két pénzérmés példát! Itt \(X=\{FF, FI, IF, II\}\) a kimenetelek halmaza. Az összes közlések \(Y\) halmaza az \(X\) részhalmazainak felel meg, de ebből csak az \(A=\{FF, FI, IF\}\) eseményhez tartozó \(y_A \in Y\) közlés („van köztük fej”) és a \(B=\{FI, IF, II\}\) eseményhez tartozó \(y_B \in Y\) közlés („van köztük írás”) valósul meg pozitív valószínűséggel.5 A kérdés az, hogy mennyi a valószínűsége, hogy a másik is fej, ha a közlő elárulta, hogy van köztük fej. Ez a \(P(FF \mid y_A)\) feltételes valószínűség.
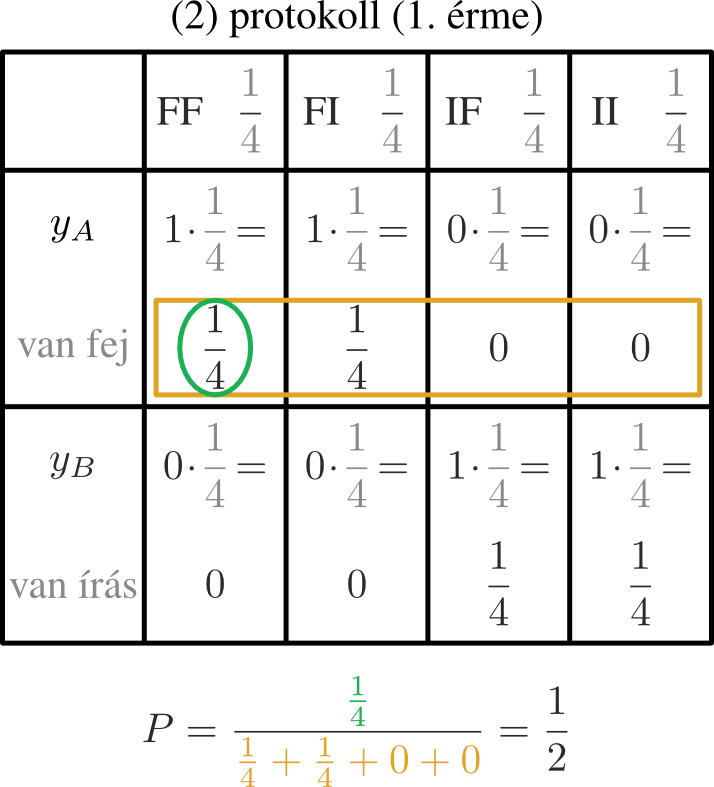
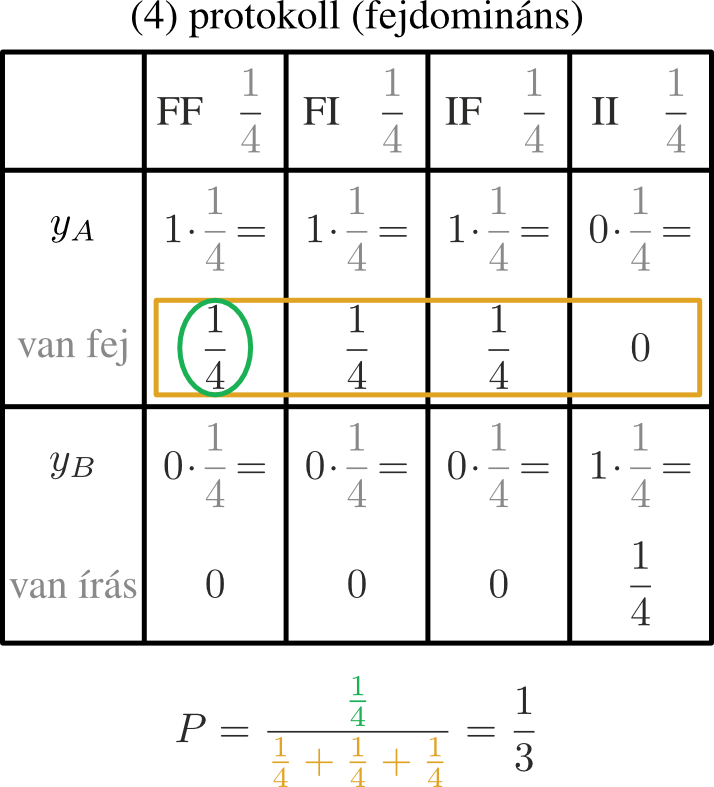
Három lényegesen különböző közlési protokollt említettünk (az eredeti számozásunkkal: (1), (2) és (4)), ezeket sorra az 5., 6., 7. ábrákon foglaltuk össze. [4]
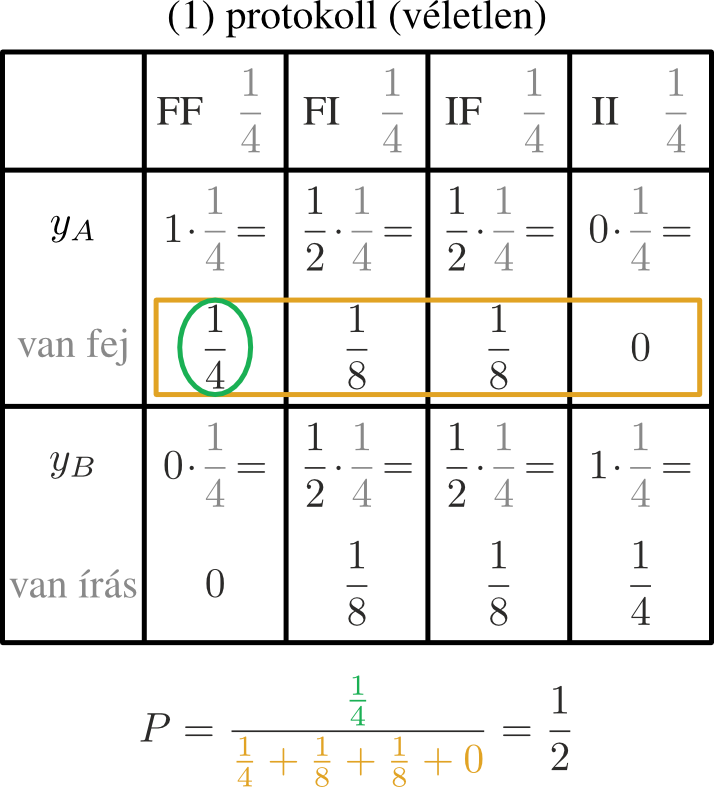
(1) (5. ábra) \(FI\), illetve \(IF\) esetén véletlenszerűen dönti el a közlő, hogy „van köztük fej” vagy „van köztük írás” legyen a közlése. Azaz, annak a valószínűsége, hogy közli, hogy van fej, ha \(FI\), illetve \(IF\) következett be, egyaránt \(1/2\) (ez a \(P(y_A \mid FI)\), illetve \( P(y_A \mid IF)\) feltételes valószínűség). Tehát annak a valószínűsége, hogy \(FI\) (illetve \(IF\)) következett be és közli, hogy van fej, \((1/2) \cdot (1/4)=1/8\) (ez a \(P (FI \cap y_A)\), illetve \(P (IF \cap y_A)\) együttes bekövetkezés valószínűsége). Ezzel a protokollal \(P=1/2\) annak a valószínűsége, hogy mindkét érme fej, ha azt mondta a közlő, hogy „van köztük fej”.
(2) (6. ábra) Az első érme értékét mondja a közlő. Azaz, 1 annak a valószínűsége, hogy közli, hogy van fej, ha \(FI\) következett be, tehát annak a valószínűsége, hogy \(FI\) következett be és közli, hogy van fej, \(1 \cdot (1/4)=1/4\). \(IF\) esetén ezek a valószínűségek 0-k, hiszen az első érme nem fej. Ezzel a protokollal szintén \(P=1/2\) annak a valószínűsége, hogy mindkét érme fej, ha azt mondta a közlő, hogy „van köztük fej”.
(4) (7. ábra) Fejdomináns protokoll, \(FI\), illetve \(IF\) esetén is 1 valószínűséggel azt mondja a közlő, hogy „van köztük fej”. Ezzel a protokollal \(P=1/3\) annak a valószínűsége, hogy mindkét érme fej, ha azt mondta a közlő, hogy „van köztük fej”. Azaz ilyenkor a \(P(FF \mid y_A)\) feltételes valószínűség (mindkettő fej, ha azt mondta a közlő, hogy „van köztük fej”) megegyezik a \(P(FF \mid A)\) feltételes valószínűséggel (mindkettő fej, ha van köztük fej).
A háromféle protokollal háromféle módon kétféle eredményt kaptunk.
2. példa. A Monty Hallnál vajon mik a kimenetelek (\(X\)) és a közlések (\(Y\))? Rögzítsük, hogy a játékos eredetileg mindig az \(A\) ajtót választja ki, úgyis csak az számít, hogy a választásához képest hol helyezkedik el a nyeremény. Ez lesz a véletlen kísérlet, vagyis az, hogy hol van a nyeremény: \(X=\{A, B, C\}\), ahol \(A\) (illetve \(B\), \(C\)) jelöli azt a kimenetelt, hogy az \(A\) (illetve \(B\), \(C\)) ajtó mögött van a nyeremény.
A közlés az, hogy a játékvezető (közlő) kinyit egy ajtót. Ha a \(C\) ajtót nyitja ki, és ott a nyeremény, ezzel a \(C\) eseményt közli, tehát ez a kimenetel \(y_C \in Y\). Ha a \(C\) ajtót nyitja ki, és az üres, ezzel a \(\overline{C}=\{A, B\}\) eseményt közli (nem a \(C\) ajtó mögött van a nyeremény), ez a kimenetel tehát \(y_{\overline{C}} \in Y\). Ugyanígy az \(A\) és a \(B\) ajtókra is van két-két közlési kimenetelünk, \(y_A, y_{\overline{A}}, y_C, y_{\overline{C}} \in Y\). Azonban az \(A\) ajtót soha nem nyitja ki, mivel ezt választotta eredetileg a játékos, ezért \[\displaystyle P(y_A)=P(y_{\overline{A}})=0. \]
A kérdést úgy lehet feltenni, hogy a közlés után mennyi a valószínűsége, hogy az eredetileg kiválasztott \(A\) ajtó mögött van a nyeremény. Ez a \(P(A \mid y_{\overline{B}})\), illetve \(P(A \mid y_{\overline{C}})\) feltételes valószínűség attól függően, hogy a \(B\) vagy a \(C\) ajtót mutatta meg (üresen) a közlő. (\(P(A \mid y_{B})\), illetve \(P(A \mid y_{C})\) is lehetne, de ez 0, hiszen ilyenkor a közlő megmutatja a nyereményt a \(B\), illetve \(C\) ajtó mögött, tehát 0 valószínűséggel van \(A\) mögött.)
Kétféle közlési protokollt említettünk, ezeket a 8., 9. ábrákon foglaltuk össze. [5]


Ha a nyeremény a kiválasztott \(A\) ajtó mögött van (első oszlop), akkor a két protokoll megegyezik: a \(B\) és a \(C\) ajtók közül véletlenszerűen nyit ki egyet a közlő, és az üres. Tehát annak a valószínűsége, hogy a \(B\), illetve \(C\) ajtót mutatja meg üresen, ha az \(A\) mögött van a nyeremény, \[\displaystyle P(y_{\overline{B}} \mid A)=P(y_{\overline{C}} \mid A)=\frac{1}{2},\] azaz annak a valószínűsége, hogy az \(A\) mögött van a nyeremény, és a \(B\), illetve \(C\) ajtót mutatja meg üresen, \[\displaystyle P(A \cap y_{\overline{B}})=P(A \cap y_{\overline{C}})=\frac{1}{2} \cdot \frac{1}{3}=\frac{1}{6}. \]
A táblázatokban sok 0 szerepel kézenfekvő okokból. Például, 0 annak a valószínűsége, hogy a közlő nyereményt mutat meg a \(B\), illetve \(C\) ajtó mögött, ha az az \(A\) mögött van; ha a \(B\) ajtó mögött van a nyeremény, akkor azt nem tudja üresen megmutatni a közlő; ha a \(C\) mögött van a nyeremény, akkor nem tudja megmutatni a közlő, hogy a \(B\) mögött van és így tovább.
A két protokoll csak akkor tér el, ha nyeremény a \(B\) vagy a \(C\) ajtó mögött van (második és harmadik oszlopok a táblázatokban).
Első (eredeti) protokoll (8. ábra): A közlő mindenképp azt az ajtót mutatja meg, amely mögött nincsen nyeremény. Tehát \[\displaystyle P(y_{C} \mid C)=0, \text{ tehát } P(C \cap y_C)=0, \] mivel biztosan nem mutatja a meg a közlő a \(C\) mögött rejtőző nyereményt, és \[\displaystyle P(y_{\overline{C}} \mid B)=1, \text{ azaz } P(B \cap y_{\overline{C}})=1 \cdot \frac{1}{3}=\frac{1}{3}, \] vagyis ha \(B\) mögött van a nyeremény, akkor biztosan a \(C\) ajtót nyitja ki és az üres. Ugyanez a helyzet \(C\) és \(B\) szerepének felcserélésvel is (szimmetrikus a szerepük).
Ebben a változatban \(1/3\) annak a valószínűsége, hogy az eredetileg kiválasztott \(A\) ajtó mögött van a nyeremény, ha a \(C\) ajtót nyitotta ki a közlő és az üres (\(B\)-vel ugyanígy van). Tehát, megéri váltani, hiszen \(1/3=33{,}3\%\) az esélye, hogy az eredetileg választott \(A\) ajtó mögött van a nyeremény, és \(2/3=66{,}6\%\), hogy a másik csukva maradt ajtó mögött van.
Második (módosított) protokoll (9. ábra):} A közlő a ki nem választott \(B\) és \(C\) ajtók közül mutat meg egyet véletlenszerűen, és ha amögött van a nyeremény, akkor azt közli (hiszen meglátja a játékos a nyereményt), ha meg üres, akkor azt. Tehát \[\displaystyle P(y_{\overline{C}} \mid B)=P(y_B \mid B)=\frac{1}{2}, \text{ azaz } P(B \cap y_{\overline{C}})=P(B \cap y_B)=\frac{1}{2} \cdot \frac{1}{3}=\frac{1}{6}, \] és ugyanez a helyzet \(B\) és \(C\) szerepének felcserélésvel is.
Ebben a változatban \(1/2\) annak a valószínűsége, hogy az eredetileg kiválasztott \(A\) ajtó mögött van a nyeremény, ha a \(C\) ajtót nyitotta ki a közlő és az üres (\(B\)-vel ugyanígy van). Tehát 50% lesz az eredeti választás nyerési valószínűsége, ha a játékvezető véletlenszerűen választ ajtót. Ilyenkor mindegy, hogy a játékos vált-e, nem növekszik és nem is csökken a nyerés valószínűsége.
A két protokollal kétféle megoldást kapunk annak a valószínűségére, hogy az eredetileg kiválasztott \(A\) ajtó mögött van a nyeremény, ha a \(C\) ajtót nyitotta ki a közlő, és az üres (\(B\)-vel ugyanígy van).
Hangsúlyozzuk ismét, hogy a játékos számára a két folyamat ugyanúgy néz ki: a játékvezető kinyit egy ki nem választott ajtót, és az üres. A játékos tehát nem látja, hogy mi alapján választ a játékvezető, azaz, hogy mi a közlési protokoll. Akkor derülne ki számára (anélkül, hogy a játékvezető elárulná), ha sokszor megismételnék a kísérletet, ugyanis a második protokollal a játékvezető időnként rányitna a nyereményre. Ez az igazi különbség a kétféle protokoll között, ami egyetlen szerencsésen alakult kísérlet alapján nem látszik.
3. példa. A „Van két gyerekem, az egyik lány …” feladatban az (1)–(5) protokollok nem újak, hiszen megfelelnek a kétpénzérmés feladat két különböző eredményre vezető három protokolljának.
A (6)–(8) protokollok voltak azok, amikor az apa hozzáteszi, hogy „… és Annának hívják”, illetve, hogy „… és hétfőn született” stb. Amint azt megállapítottuk, ezekben az esetekben egy bővebb eseményteret kell vennünk, hogy értelmezhető legyen a közlés, így kapjuk a 4. ábrán látható 9 kimenetelből álló \(X\) halmazt. De mi voltaképpen a közlési protokoll? Bár nem hangsúlyoztuk, az ábrán és az (1) egyenletben ezt a feltételes valószínűséget számoltuk ki: mennyi annak a valószínűsége, hogy a másik gyerek is lány, ha az egyik lány és Annának hívják, illetve hétfőn született? Ezáltal kimondatlanul feltételeztük, hogy az apa a domináns protokollt használja: ha az egyik gyerek lány és teljesül rá az extra tulajdonság (Anna, illetve hétfőn született), akkor az apa biztosan ezt fogja közölni. A kétgyerekes paradoxonról szóló általunk ismert leírások és videók is automatikusan (különösebb indoklás nélkül) így számolnak. Érdekes, hogy részletesebb elemzés nélkül fel sem tűnik, hogy itt van egy extra feltételezés.
A (6)–(8) protokollok tehát az eseményteret és a szóban forgó eseményeket változtatják meg, de mint közlési protokollok nem újak számunkra, domináns közlési protokollok a lány-és-Anna, illetve lány-és-hétfőn született és a többi eseményekre nézve. Ez azt is jelenti, hogy még egyet lehetne csavarni a kérdésen: a (6)–(8)-ban szereplő közléseket másmilyen (nem domináns) közlési protokollal is lehetne tekinteni.
5. Tanulság
Alaposan kielemeztük a Monty Hall, a két pénzérmés és a fiú–lány paradoxonok különböző verzióit, és megmutattuk, hogy a kérdéses valószínűség lényegesen függ a közlés módjától, kontextusától. Emiatt van az, hogy az említett problémák pontos megfogalmazásában már egy apró eltérés is teljesen más megoldásra vezet. A lehetséges változatok között szerepelnek olyanok is, amelyek a „naiv” megoldásra vezetnek, vagyis arra, amit különösebb gondolkodás nélkül rávágnánk. Azonban ezek a naiv megoldások is igen változatosan jönnek létre.
A felvetett kérdések zűrzavarának kezelésére bevezettünk egy egyszerű modellt, amit közlési protokollnak neveztünk. Fontos, hogy a közlési protokoll egyetlen kísérlet során nem látszik, miközben ezen múlik a kérdéses valószínűség. A közlési protokollt sokszor megismételt kísérletsorozattal lehet láthatóvá tenni.
A cikk második részében megvizsgáljuk a közlési protokollok általános tulajdonságait, és megállapítjuk, hogy egy \(B\) esemény közlése milyen protokollok esetén egyenértékű a \(B\) esemény bekövetkezésével. A tapasztalataink alapján felülvizsgáljuk a szokásos tankönyvi feladatokat a feltételes valószínűség (Bayes-tétel) témakörben, és közlünk egy összefoglalót a közlési protokollunk szakirodalmi megjelenéseiről, előzményeiről.
❖
A cikk lejegyzője Pintér Gergő matematikus. Minden szinten űzi és tanítja a matekot. Topológia és szingularitáselmélet témában doktorált, jelenleg egy fizikus kutatócsoporttal kvantumrendszerek topológiai jellemzőit vizsgálja. Főleg különböző területek kapcsolódásai érdeklik, a MateMorfózis előadássorozat keretében szórakoztató fesztiválműfajt formált a „felsőbb” matematikából. Két ismeretterjesztő könyve jelent meg, az Új világok teremtése (geometriai képzetek és képződmények), illetve A Számok rejtett építőkövei (a prímek).
Régóta foglalkoztattak a Monty Hall paradoxon különböző változatai, ezekről már majdnem 20 éve, az ELTE matematikus szak elején hallottam társamtól, Strenner Balázs matematikustól. Néhány éve az Ismeretterjesztő Matematika kurzuson Keszthelyi Gabriella valószínűségszámítás témájú előadása alapján ismét előkerült ez a téma, azóta érdekelt, hogyan lehetne a különböző paradoxonok különböző változatait egységes keretben átfogóan kezelni. Nemrég pedig Németh Hanna matematikus videója és Keszthelyi Gabriella (BME Matematika Intézet): Milyen színű a valószínű? című könyvében szereplő leírás váltott ki egy közös diskurzust Gabin és Hannán kívül Bodnár József matematikussal, Lőrincz Lénárd fizikussal, Konczer József fizikussal és Mosóczi András matematikussal (Mateking). E diskurzus összefoglalása ez a kétrészes cikk. A közös ötletelések után kialakult ábrák kivitelezője Somogyi-Csizmazia Eszter. Köszönöm nekik a sok segítséget!
Pintér Gergő
Függelék
Ebben a függelékben közöljük a cikkben található ábrákhoz tartozó levezetéseket és számolásokat, és további kiegészítéseket a kétgyerekes problémához.
[1] Monty Hall-probléma
1. ábra. „Naiv” Monty Hall: Mennyi a valószínűsége, hogy a nyeremény az \(A\) ajtó mögött van, ha nincs a \(C\) ajtó mögött? \(A\), \(B\), illetve \(C\)-vel jelölve azt az eseményt, hogy a nyeremény a megfelelő ajtó mögött van, és \(\overline{C}\)-vel azt, hogy nincs a \(C\) ajtó mögött, az említett feltételes valószínűség \[ P(A \mid \overline{C})=\frac{P(A \cap \ \overline{C})}{P( \overline{C})}=\frac{P(A)}{P(\overline{C})}=\frac{33{,}3\%}{66{,}6\%}=\frac{1}{2}, \] azaz 50%. (Itt felhasználtuk, hogy ha az \(A\) mögött van a nyeremény, akkor nincs a \(C\) mögött, ezért \(A \cap \overline{C}=A\).)
[2] Van fej
2. ábra. Mennyi a valószínűsége, hogy mindkét érme fej, ha van köztük fej? Jelöljük \(A\)-val azt az eseményt, hogy van köztük fej, tehát \(A=\{FF, FI, IF\}\), így a kérdés \(FF\) valószínűsége, ha \(A\) bekövetkezett: \[ P(FF \mid A)=\frac{P(FF \cap A)}{P(A)}=\frac{P(FF)}{P(A)}=\frac{25\%}{75\%}=\frac{1}{3}\approx33{,}3\%. \] (Kissé slendriánul \(FF\)-fel jelöltem az \(\{FF\}\) egyelemű halmazt is, azaz azt az eseményt, hogy az \(FF\) kimenetel következett be.)
[3] Van két gyerekem az egyik lány.
Egy apa közli: „Van két gyerekem, az egyik lány…” Mennyi a valószínűsége, hogy a másik is lány? A (6)–(8) protokolloknál az apa kiegészíti a közlését egy olyan információval, amely teljesen irrelevánsnak tűnik abból a szempontból, hogy a másik gyerek is lány-e:
(6) A mondata így folytatódik: „Van két gyerekem, az egyik lány, és Annának hívják.”
(6′) A mondata így folytatódik: „Van két gyerekem, az egyik lány, és január első felében született.”
(7) A mondata így folytatódik: „Van két gyerekem, az egyik lány, és hétfőn született.”
(8) A mondata így folytatódik: „Van két gyerekem, az egyik lány, és délután (dél és éjfél között) született.”
Mint azt megállapítottuk, ezekben az esetekben nem a közlési protokoll számít, pontosabban, kimondatlanul feltételezni szokták a „domináns” protokollt. A kérdés tehát szimplán a feltételes valószínűség: mennyi annak a valószínűsége, hogy a másik gyerek is lány, ha az egyik lány és teljesül rá az extra tulajdonság (Annának hívják, hétfőn született stb.)? Ez a kérdés vezet meglepő bonyodalmakhoz, amiknek a tárgyalása a cikk fő gondolati fonalából, hiszen nem a közlési protokollal kapcsolatos.
4. ábra: A (6′), (7), (8) esetben elárul az apa egy olyan tulajdonságot, amely a lányok \(p\)-szeresére teljesül egymástól függetlenül6 (az nem lényeges, hogy fiúkra is teljesülhet-e). (6′) esetén \(p=0{,}04\), (7) esetén \(p=1/7\), (8) esetén \(p=1/2\).
Jelölje \(\mathcal{F}\) azt, hogy egy gyerek fiú, \(\mathcal{L}_a\) azt, hogy lány és teljesül rá ez a tulajdonság, \(\mathcal{L}_n\) pedig azt, hogy lány, és nem tljesül. Ekkor a két gyerekre 9 lehetőségünk van. Mivel a függetelenség miatt a két gyerek valószínűségeit össze kell szoroznunk, az ábrán látható 9 eset valószínűségei: \[\displaystyle P(\mathcal{F}\mathcal{F})=\frac{1}{4}, \ P(\mathcal{F} \mathcal{L}_a)=P(\mathcal{L}_a F)=p \cdot \frac{1}{4}, \ P(\mathcal{F} \mathcal{L}_n)=P(\mathcal{L}_n \mathcal{F})=(1-p) \cdot \frac{1}{4}, \] \[\displaystyle P(\mathcal{L}_n \mathcal{L}_a)=P(\mathcal{L}_a \mathcal{L}_n)=p \cdot (1-p) \cdot \frac{1}{4}, \ P(\mathcal{L}_n \mathcal{L}_n)=(1-p)^2 \cdot \frac{1}{4}, \ P(\mathcal{L}_a \mathcal{L}_a)=p^2 \cdot \frac{1}{4}. \]
A közlés szerint legalább az egyik gyerek \(\mathcal{L}_a\) (azaz lány és teljesül rá az extra tulajdonság), tehát az \[\displaystyle A=\{\mathcal{F} \mathcal{L}_a, \mathcal{L}_a \mathcal{F}, \mathcal{L}_a \mathcal{L}_n, \mathcal{L}_n \mathcal{L}_a, \mathcal{L}_a \mathcal{L}_a \} \] esemény bekövetkezett, és azt kérdezzük, hogy a másik gyerek is lány-e, azaz \[\displaystyle B=\{ \mathcal{L}_a \mathcal{L}_n, \mathcal{L}_n \mathcal{L}_a, \mathcal{L}_a \mathcal{L}_a \} \] is teljesül-e. Tehát annak a valószínűsége, hogy a másik gyerek is lány, \[\displaystyle P=P(B \mid A)=\frac{\frac{1}{4} \cdot (2 \cdot p \cdot (1-p)+p^2)}{\frac{1}{4} \cdot (2 \cdot p+2 \cdot p \cdot (1-p)+p^2)}=\frac{2-p}{4-p}. \]
Ha az extra tulajdonság \(p\) gyakoriságát 0-tól 1-ig változtatjuk, a \(P\) valószínűség megvalósít egy átmenetet \(1/2\) és \(1/3\) között.
A (6) esetben az a lényeges különbség, hogy a két gyereknek nem lehet ugyanaz a neve. Ennek egyik lehetséges kezelése, hogy nem foglalkozunk ezzel a kitétellel, és a (6′) modelljét alkalmazzuk, azaz a gyerekek egymástól függetlenül kapnak nevet. Ekkor pici valószínűséggel egy lány–lány testvérpár mindkét tagját hívhatják Annának, de ez nem befolyásolja lényegesen az eredményt (amely a \(p=0{,}04\)-hez tartozó \(\approx 50\%\)). Például Keszthelyi Gabriella így jár el a könyvében (97. oldal).
Másik lehetőség, hogy ténylegesen egy olyan modellt használunk, amiben egy testvérpár két tagját nem hívják ugyanúgy, mint például ebben és ebben a videóban. Meglepő, hogy ilyen modell egyáltalán létezik, hiszen ez a kitétel ellentmond annak, hogy a gyerekek egymástól függetlenül kapnak nevet. De van olyan megoldás, amely szerint a lehető legfüggetlenebbek, ezzel a kitétellel!
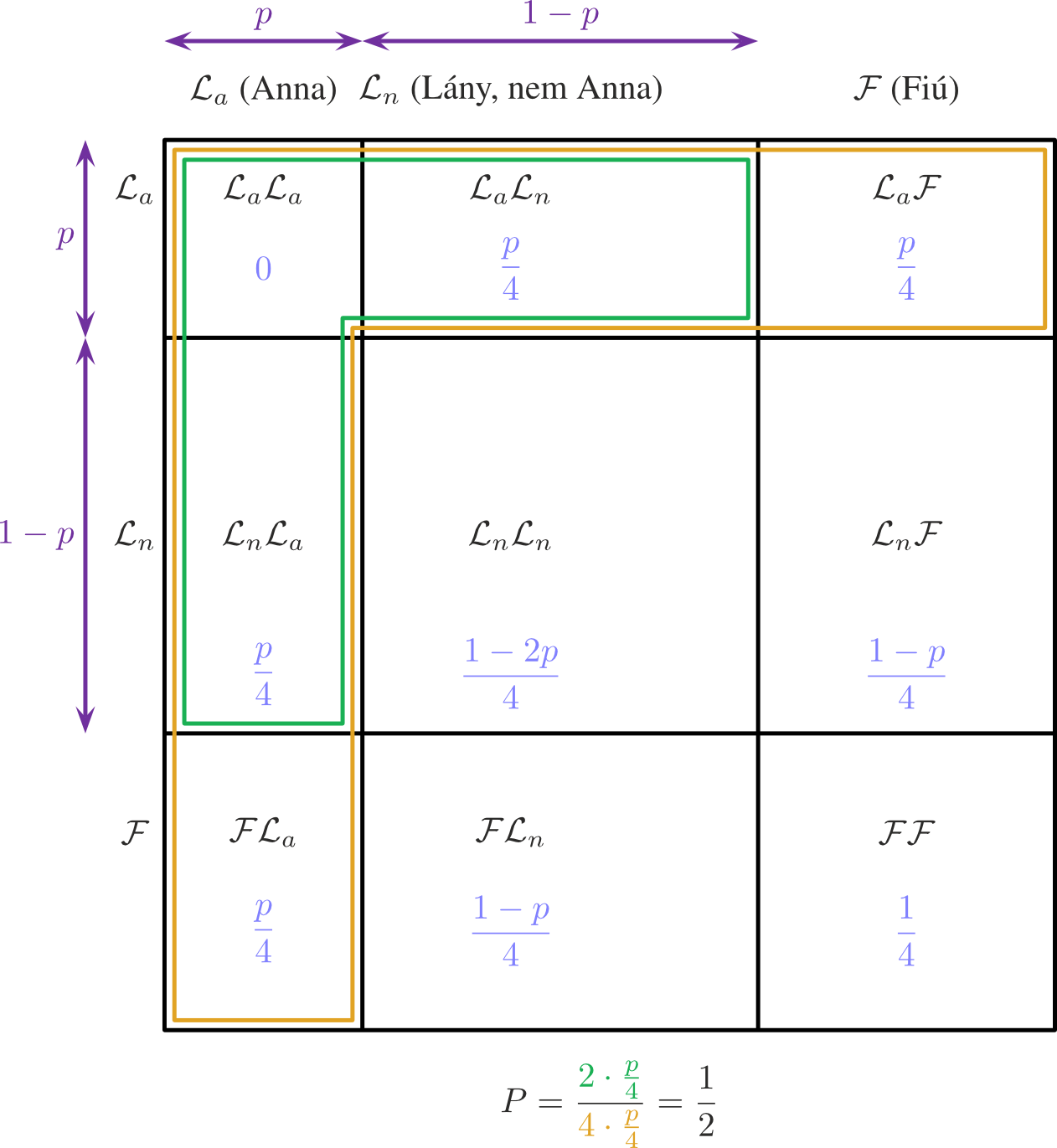
Az előzőekhez hasonlóan, jelölje \(\mathcal{F}\) azt, hogy egy gyerek fiú, \(\mathcal{L}_a\) azt, hogy lány és Anna, \(\mathcal{L}_n\) pedig azt, hogy lány és nem Anna. Tegyük fel, hogy egy lányt \(p\) valószínűséggel neveznek Annának (másképpen: az Anna név előfordulásának gyakorisága a lányok között \(p\)).
Töltsük ki a táblázatot! Ha az egyik gyerek fiú, akkor ugyanaz a valószínűség, mint a 4. ábrán. Tehát a 4. és 4. a) ábrák csak a bal felső negyedben különböznek egymástól (lány–lány). A kitételünk szerint nem hívhatják egy testvérpár mindkét tagját Annának, tehát \[\displaystyle P(\mathcal{L}_a \mathcal{L}_a)=0, \] A lány–lány testvérpár valószínűsége \(1/4\), és ezen belül még \(p\) annak a valószínűsége, hogy az egyik lány neve Anna. Ekkor viszont a másik lány automatikusn nem Anna lesz, tehát \[P(\mathcal{L}_n \mathcal{L}_a)=P(\mathcal{L}_a \mathcal{L}_n)=\frac{p}{4}.\] Két nem Anna lánytestvér valószínűsége ebből már következik: \[\displaystyle P(\mathcal{L}_n \mathcal{L}_n)=\frac{1}{4}-2 \cdot \frac{p}{4}=\frac{1-2p}{4}. \]
Ugyanúgy, ahogy a (6′)–(8) esetben is, legyen \(A\) az az esemény, hogy legalább az egyik gyerek lány és Anna, és legyen \(B\) az, hogy ezen felül még a másik gyerk is lány. A kérdéses valószínűség tehát \[\displaystyle P=P(B \mid A)=\frac{2 \cdot \frac{p}{4}}{4 \cdot \frac{p}{4}}=\frac{1}{2}. \] Így tehát egzaktul \(1/2\) annak a valószínűsége, hogy a másik gyerek is lány, nem kell feltételezni azt sem, hogy \(p\) pici. Persze \(p\leq 1/2\) kell, különben \(P(\mathcal{L}_n \mathcal{L}_n)\) valószínűsége negatív lenne, de más megkötésünk nincsen.
E cikk születése során Bodnár József jegyezte meg, hogy miért bajlódik mindenki a függetlenséggel, amely csak közelítőleg \(1/2\) valószínűségre vezet, amikor pedig így is eljárhatunk. Az oka talán az, hogy ennek a modellnek a megvalósíthatósága nem magától értetődő. Egy adott kétgyerekes családokból álló populáció esetén hogyan adjunk nevet a gyerekeknek?
A független ((6′)-nek megfelelő) megoldásban ez egyszerű: minden gyereknek kisorsolunk egyet a nemének megfelelő nevek közül. Ezt megtehetjük egyenletesen, azaz \(n\) lánynév esetén minden lány \(p=1/n\) valószínűséggel kap egy-egy nevet, vagy súlyozhatjuk is őket, ekkor az \(i\). lánynév valószínűsége \(p_i\) minden egyes lánygyerek esetén, egymástól függetlenül.
De hogyan járjunk el ahhoz, hogy testvérek ne kapjanak azonos nevet? Például, azonos nemű gyerekek esetén az idősebbik (feltesszük, hogy ikrek nincsenek) kap egy nevet \(p=1/n\) valószínűséggel, majd ezt a nevet kivesszük a kalapból, és a kisebb testvér a maradék \(n-1\) névből kap egyet \(1/(n-1)\) valószínűséggel. Másképpen: a nem-azonos lánynévpárok közül választunk egyenlő valószínűséggel. (Előírt \(p_i\) valószínűségek esetén a megfelelő módosítás szükséges.)
Bodnár József másik érdekes észrevétele ezzel kapcsolatban, hogy ez a feladat (Annának hívják) lényegében ugyanaz, mint a cikk főszövegében (3)-sal jelölt közlés: Az apa a nappalijukban mesél: „Van két gyerekem…”, és ekkor kiszalad az egyik gyerek a kisszobából, történetesen egy lány. Valóban: a családoknak csak egy kis részénél történik meg az, hogy kiszalad az egyik gyerek – akárcsak az, hogy Annának hívják –, és mindkét gyerek nem szalad ki egyszerre, tehát csak az egyikükről beszélünk – akárcsak az Anna esetén. Itt látszólagos ellentmondás lehet, hogy a (3)-mas verziót egy közlési protokollként kezeltük, míg a (6)-osat nem, de ennek továbbgondolását már az olvasóra bízzuk.
[4] Közlési protokollok
1. példa. Nézzük először a két pénzérmés példát! Itt \(X=\{FF, FI, IF, II\}\) a kimenetelek halmaza. Az összes közlések \(Y\) halmaza az \(X\) részhalmazainak felel meg, de ebből csak az \(A=\{FF, FI, IF\}\) eseményhez tartozó \(y_A \in Y\) közlés („van köztük fej”) és a \(B=\{FI, IF, II\}\) eseményhez tartozó \(y_B \in Y\) közlés („van köztük írás”) valósul meg pozitív valószínűséggel.5 A kérdés az, hogy mennyi a valószínűsége, hogy a másik is fej, ha a közlő elárulta, hogy az egyik fej. Ez a \(P(FF \mid y_A) \) feltételes valószínűség.
Három lényegesen különböző közlési protokollt említettünk (az eredeti számozásunkkal: (1), (2) és (4)), ezeket sorra az 5., 6., 7. ábrákon foglaltuk össze, és itt leírjuk formálisan is.
(1) (5. ábra) \(FI\), illetve \(IF\) esetén véletlenszerűen dönti el a közlő, hogy „van köztük fej” vagy „van köztük írás” legyen a közlése. Azaz, annak a valószínűsége, hogy közli, hogy van fej, ha \(FI\), illetve \(IF\) következett be, egyaránt \[\displaystyle P(y_A \mid FI)=P(y_A \mid IF)=\frac{1}{2}, \] tehát annak a valószínűsége, hogy \(FI\) (illetve \(IF\)) következett be és közli, hogy van fej, \[\displaystyle P(FI \cap y_A)=P(IF \cap y_A)=\frac{1}{2} \cdot \frac{1}{4}=\frac{1}{8}. \]
(2) (6. ábra) Az első érme értékét közli. Azaz, annak a valószínűsége, hogy közli hogy van fej, ha \(FI\) következett be, \[\displaystyle P(y_A \mid FI)=1, \] tehát annak a valószínűsége, hogy \(FI\) következett be és közli, hogy van fej, \[\displaystyle P(FI \cap y_A)=1 \cdot \frac{1}{4}=\frac{1}{4}. \] \(IF\) esetén ezek a valószínűségek 0-k, hiszen az első nem fej: \[\displaystyle P(y_A \mid IF)=0, \text{ tehát } P(IF \cap y_A)=0. \]
(4) (7. ábra) Fejdomináns protokoll, \(FI\), illetve \(IF\) esetén is azt mondja, hogy „van köztük fej”. Azaz, \[\displaystyle P(y_A \mid FI)=P(y_A \mid IF)=1, \text{ tehát } P(FI \cap y_A)=P(IF \cap y_A)=\frac{1}{4}. \]
A háromféle protokoll csak ezekben az \(FI\), illetve \(IF\) kimenetelekhez tartozó középső oszlopokban különbözik, a két szélén ugyanaz áll mindhárom esetben. Azaz, \(FF\) esetén biztosan azt mondja, hogy van fej: \[\displaystyle P(y_A \mid FF)=1, \text{ tehát } P(FF \cap y_A)=\frac{1}{4}, \] és \(II\) esetén biztosan nem mondja azt: \[\displaystyle P(y_A \mid II)=0, \text{ tehát } P(II \cap y_A)=0. \] Továbbá, \[\displaystyle P(y_B \mid b)=1-P(y_A \mid b) \] teljesül minden \(b \in X\)-re (azaz \(b=FF, FI, IF, II\) esetén), vagyis pontosan akkor mondja a közlő, hogy „van köztük írás”, ha nem azt mondja, hogy „van köztük fej”. Amint látni fogjuk, ez egy sarkalatos pontja a közlési protokolloknak.
Mi is volt a kérdés? Hogy mennyi a valószínűsége, hogy a másik dobás is fej, ha azt közölték, hogy van köztük. A háromféle protokollal háromféle módon kétféle eredményt kapunk. Először is számoljuk ki mindegyik protokollra a táblázatban sárgával bekeretezett sorban szereplő valószínűségek összegét, ez annak a valószínűsége, hogy a közlő azt mondja, hogy „van köztük fej”: \[\displaystyle\begin{gather*} P(y_A)=P(FF \cap y_A)+P(FI \cap y_A)+P(IF \cap y_A)+P(II \cap y_A)=\\ =\begin{cases} {\frac{1}{4}+\frac{1}{8}+\frac{1}{8}+0}=\frac{1}{2} & \text{az (1) protokollal} \\ {\frac{1}{4}+\frac{1}{4}+0+0}=\frac{1}{2} & \text{a (2) protokollal} \\ {\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+0}=\frac{3}{4} & \text{a (4) protokollal,} \end{cases} \end{gather*} \] Ebből a kérdéses valószínűség \[\displaystyle P(FF \mid y_A)=\frac{P(FF \cap y_A)}{P(y_A)}=\begin{cases} \frac{1/4}{1/4+1/8+1/8+0}=\frac{1}{2} & \text{az (1) protokollal} \\ \frac{1/4}{1/4+1/4+0+0}=\frac{1}{2} & \text{a (2) protokollal} \\ \frac{1/4}{1/4+1/4+1/4+0}=\frac{1}{3} & \text{a (4) protokollal,} \end{cases} \] összhangban az előző eredményeinkkel.
[5] Közlési protokollok
2. példa. A Monty Hallnál vajon mik a kimenetelek (\(X\)) és a közlések (\(Y\))? Rögzítsük, hogy a játékos eredetileg mindig az \(A\) ajtót választja ki, úgyis csak az számít, hogy a választásához képest hol helyezkedik el a nyeremény. Ez lesz a véletlen kísérlet, vagyis az, hogy hol van a nyeremény: \(X=\{A, B, C\}\), ahol \(A\) (illetve \(B\), \(C\)) jelöli azt a kimenetelt, hogy az \(A\) (illetve \(B\), \(C\)) ajtó mögött van a nyeremény.
A közlés az, hogy a játékvezető (közlő) kinyit egy ajtót. Ha a \(C\) ajtót nyitja ki, és ott a nyeremény, ezzel a \(C\) eseményt közli, tehát ez a kimenetel \(y_C \in Y\). Ha a \(C\) ajtót nyitja ki, és az üres, ezzel a \(\overline{C}=\{A, B\}\) eseményt közli (nem a \(C\) ajtó mögött van a nyeremény), ez a kimenetel tehát \(y_{\overline{C}} \in Y\). Ugyanígy az \(A\) és a \(B\) ajtókra is van két-két közlési kimenetelünk, \(y_A, y_{\overline{A}}, y_C, y_{\overline{C}} \in Y\). Azonban az \(A\) ajtót soha nem nyitja ki, mivel ezt választotta eredetileg a játékos, ezért \(P(y_A)=P(y_{\overline{A}})=0\).
A kérdést úgy lehet feltenni, hogy a közlés után mennyi a valószínűsége, hogy az eredetileg kiválasztott \(A\) ajtó mögött van a nyeremény. Ez a \(P(A \mid y_{\overline{B}})\), illetve \(P(A \mid y_{\overline{C}})\) feltételes valószínűség attól függően, hogy a \(B\) vagy a \(C\) ajtót mutatta meg a közlő. (\(P(A \mid y_{B})\), illetve \(P(A \mid y_{C})\) is lehetne, de ez 0, hiszen ilyenkor a közlő megmutatja a nyereményt a \(B\), illetve \(C\) ajtó mögött, tehát 0 valószínűséggel van \(A\) mögött.) Ha a játékos átvált a másik csukva maradt ajtóra, akkor a nyerés valószínűsége 1 mínusz annyi, mitha nem vált át.
Kétféle közlési protokollt említettünk, ezeket a 8., 9. ábrákon foglaltuk össze, és itt leírjuk formálisan is. Ha a nyeremény a kiválasztott \(A\) ajtó mögött van (első oszlop), akkor a két protokoll megegyezik: a \(B\) és a \(C\) ajtók közül véletlenszerűen nyit ki egyet a közlő, és az üres. Tehát annak a valószínűsége, hogy a \(B\), illetve \(C\) ajtót mutatja meg üresen, ha az \(A\) mögött van a nyeremény, \[\displaystyle P(y_{\overline{B}} \mid A)=P(y_{\overline{C}} \mid A)=\frac{1}{2}, \] azaz annak a valószínűsége, hogy az \(A\) mögött van a nyeremény, és a \(B\), illetve \(C\) ajtót mutatja meg üresen, \[\displaystyle P(A \cap y_{\overline{B}})=P(A \cap y_{\overline{C}})=\frac{1}{2} \cdot \frac{1}{3}=\frac{1}{6}. \] Annak a valószínűsége, hogy nyereményt mutat a \(B\), illetve \(C\) ajtó mögött, ha az az \(A\) mögött van, természetesen 0: \[\displaystyle P(y_B \mid A)=P(y_C \mid A)=0, \text{ azaz } P(A \cap y_B)=P(A\cap y_C)=0. \] Továbbá \[\displaystyle P(y_{\overline{B}} \mid B)=P(y_{\overline{C}} \mid C)=0, \text{ azaz } P(B \cap y_{\overline{B}})=P(C \cap y_{\overline{C}})=0 \] is mindig teljesül, hiszen ha a \(B\) ajtó mögött van a nyeremény, akkor azt nem tudja üresen megmutatni a közlő, és ugyanígy \(C\)-vel is. Hasonlóképp, \[\displaystyle P(y_C \mid B)=P(y_B \mid C)=0, \text{ tehát } P(B \cap y_C)=P(C \cap y_B)=0 \] is mindig teljesül, hiszen ha a \(C\) mögött van a nyeremény, akkor nem tudja megmutatni a közlő, hogy a \(B\) mögött van és viszont.
A két protokoll csak akkor tér el, ha a nyeremény a \(B\) vagy a \(C\) ajtó mögött van (második és harmadik oszlopok a táblázatokban).
Első (eredeti) protokoll (8. ábra): A közlő mindenképp azt az ajtót mutatja meg, amely mögött nincsen nyeremény. Tehát \[\displaystyle P(y_{C} \mid C)=0, \text{ tehát } P(C \cap y_C)=0, \] mivel biztosan nem mutatja meg a közlő a \(C\) mögött rejtőző nyereményt, és \[\displaystyle P(y_{\overline{C}} \mid B)=1, \text{ azaz } P(B \cap y_{\overline{C}})=1 \cdot \frac{1}{3}=\frac{1}{3} \] vagyis ha \(B\) mögött van a nyeremény, akkor biztosan a \(C\) ajtót nyitja ki, és az üres. Ugyanez a helyzet \(C\) és \(B\) szerepének felcserélésvel is (szimmetrikus a szerepük).
Második (módosított) protokoll (9. ábra): A közlő a ki nem választott \(B\) és \(C\) ajtók közül mutat meg egyet véletlenszerűen, és ha amögött van a nyeremény, akkor azt közli (hiszen meglátja a játékos a nyereményt), ha meg üres, akkor azt. Tehát \[\displaystyle P(y_{\overline{C}} \mid B)=P(y_B \mid B)=\frac{1}{2}, \text{ azaz } P(B \cap y_{\overline{C}})=P(B \cap y_B)=\frac{1}{2} \cdot \frac{1}{3}=\frac{1}{6}, \] és ugyanez a helyzet \(B\) és \(C\) szerepének felcserélésvel is.
A két protokollal kétféle megoldást kapunk annak a valószínűségére, hogy az eredetileg kiválasztott \(A\) ajtó mögött van a nyeremény, ha a \(C\) ajtót nyitotta ki a közlő, és az üres (\(B\)-vel ugyanígy van). Először számoljuk ki mindkét protokollra a sárgával bekeretezett sorban szereplő valószínűségek összegét, ez annak a valószínűsége, hogy a \(C\) ajtót nyitja ki a közlő, és az üres: \[\displaystyle\begin{gather*} P(y_{\overline{C}})=P(A \cap y_{\overline{C}})+P(B \cap y_{\overline{C}})+P(C \cap y_{\overline{C}})=\\ =\begin{cases} {\frac{1}{6}+\frac{1}{3}+0}=\frac{1}{2} & \text{az 1. (eredeti) protokollal} \\ {\frac{1}{6}+\frac{1}{6}+0}=\frac{1}{3} & \text{a 2. (módosított) protokollal.} \end{cases} \end{gather*}\] Ebből a kérdéses valószínűség (zöld osztva sárgával) \[\displaystyle P(A \mid y_{\overline{C}})=\frac{P(A \cap y_{\overline{C}})}{P(y_{\overline{C})}}=\begin{cases} \frac{1/6}{1/6+1/3+0}=\frac{1}{3} & \text{az 1. (eredeti) protokollal} \\ \frac{1/6}{1/6+1/6+0}=\frac{1}{2} & \text{a 2. (módosított) protokollal.} \end{cases} \]
Tehát ha a játékvezető véletlenszerűen választ ajtót, akkor \(50\%\) lesz az eredeti választás nyerési valószínűsége. Ilyenkor tehát mindegy, hogy a játékos vált-e, nem növekszik a nyerés valószínűsége és nem is csökken. Ellentétben az eredeti változattal, ahol pedig megéri váltani. (\(1/3\) az esélye, hogy az eredetileg választott \(A\) ajtó mögött van a nyeremény, és \(2/3\), hogy a másik csukva maradt ajtó mögött van.)
Lábjegyzetek
1A cikk megszületésében közreműködők bemutatását ld. a cikk végén.
2Mindegyik kérdésfelvetés máshonnan származik, hiszen ismert problémák más platformokon található tárgyalásaira reagálunk, azokat gondoljuk tovább, de egyúttal össze is foglaljuk őket. Tehát az alapmodelleket nem mi találtuk ki, ezeket így szokták tárgyalni.
3A feltételes valószínűség: „\(A\) feltéve, hogy \(B\)”, azaz szemléletesen: a \(B\)-be eső kimenetelek között milyen arányban vannak az \(A\)-ba is eső kimenetelek. Formálisan: \({P(A \mid B)}={P(A \cap B)/P(B)}\). Az \(A \cap B\) metszet jelentése a két esemény együttes bekövetkezése, azaz „\(A\) és \(B\)”.
4Tartsuk szem előtt, hogy ez mind csak modell, és ezeket a szellemes feladványokat úgy találták ki, hogy többé-kevésbé életszerűen lehessen rájuk alkalmazni a modellt. Egy valós feladatot többféle módon lehet modellezni, és minden modell sok valós tényező elhanyagolásával jár. Mi most a modellválasztási problámákkal kapcsolatban egy speciális körülmányre koncentrálunk, a közlési protokollra, ezért a modellválasztással kapcsolatos többi problémát nem részletezzük, csak röviden térünk ki rájuk a függelékben.
5Pontosabban, mivel a fejdomináns protokoll esetén nem tudjuk, mit szándékozik közölni a közlő, ha nincs fej, ezért talán az \(N=\{II\}\) eseményhez tartozó \(y_N\) („nincs fej”) közlésre is szükség lehet. De inkább feltételezzük, hogy ilyenkor azt mondja a közlő, hogy van írás, azaz \(y_B\) következik be.
6Ezek a feltevések nem feltétlenül állják meg a helyüket. Például az, hogy két gyerek azonos családban ugyanabban a hónapban születik, bizonyos esetekben valószínűbb, például ikrek esetén, vagy ha a férj az otthonától távol dolgozik, és évente mindig ugyanakkor van szabadságon. Lehetséges, hogy vannak nők, akik bizonyos évszakokban termékenyebbek. Továbbá nem biztos, hogy 50% annak a valószínűsége, hogy délelőtt vagy délután születik-e a gyerek, lehet, hogy a vajúdás többször indul meg éjjel (de ez persze nem biztos). Ezek a szempontok csak példák arra, hogy az külön vizsgálatot igényelne, hogy mennyire helytálló a modell, amivel dolgozunk.}





