A 2024 júniusában megjelent cikkben olyan \(x^2+ax+b=0\) és \(x^2+ax-b=0\) alakú másodfokú egyenletpárokat vizsgáltam, amelyeknél \(a\) és \(b\) egész számok, és a két egyenlet gyökei szintén egész számok. Az alábbiakban vizsgált egyenletpárok megoldási módszere más matematikai eszközök bemutatását teszi lehetővé, tehát más szempontból érdekesek. Itt nem alkalmazunk komplex számokat a megoldások során, sokkal inkább támaszkodunk az emelt szintű érettségi követelményeire.
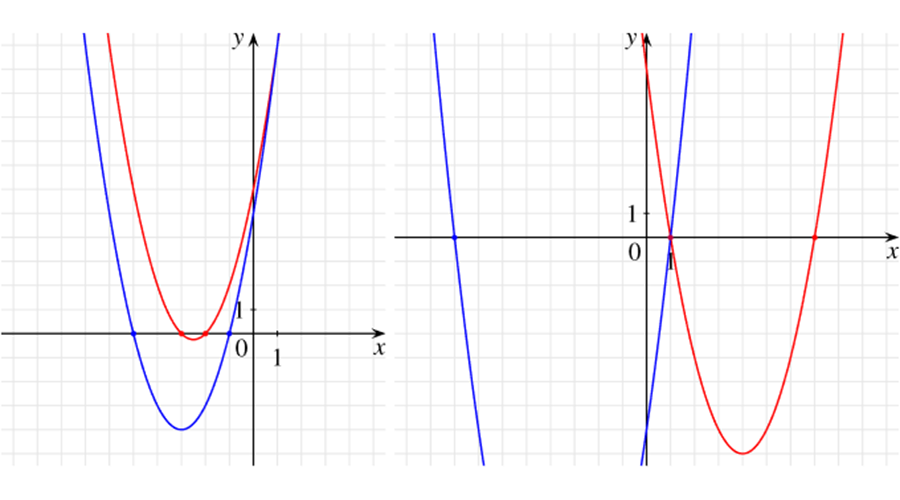
Középiskolai tanulmányok során gyakran találkozunk az \(x^2+5x+6=0\) és az \(x^2+6x+5=0\) másodfokú egyenletekkel, amelyeknek a gyökei egyaránt egész számok. Másik ilyen „szerencsés” páros a következő két egyenlet: \(x^2-8x+7=0\) és \(x^2+7x-8=0\). Mindkét esetben a konstans tag és az elsőfokú tag együtthatóját felcserélve olyan másodfokú egyenletet kaptunk, amelynek szintén egész számok a gyökei, csakúgy, mint az eredetinek. (Az alábbi ábrán a koordináta-rendszerben ábrázoltuk a fenti négy egyenlet megoldásait a függvények megrajzolásával.)

Ahogy azt a fent említett cikkben láttuk, ezúttal is felvethetjük matematika szakkörön és matematika tagozaton (vagy egyéb haladó csoportokban tanórán) az alábbi kérdéseket:
– Véges vagy végtelen sok ilyen páros létezik?
– Hogyan lehet ilyen egyenletpárokat előállítani a fenti két példán kívül (ha egyáltalán vannak)?
Ezekre a kérdésekre keressük a választ ebben a cikkben, és a probléma megoldásában a Viète-formulákat fogjuk segítségül hívni.
A probléma tehát a következő: melyek azok az \(a\) és \(b\) egész számok, amelyekre az \(x^2+ax+b=0\) és az \(x^2+bx+a=0\) másodfokú egyenletek gyökei egyaránt egész számok?
Elsőként vegyük észre, hogy ha \(a=0\), akkor az \(x^2+bx+a=0\) egyenlet gyökei 0 és \(-b\) (ezek tehát egészek), az \(x^2+ax+b=0\) egyenlet gyökei viszont pontosan akkor lesznek egészek, ha \(b\) egy négyzetszám ellentettje. Hasonlóan, ha \(b=0\), akkor \(a\)-nak egy négyzetszám ellentettjének kell lennie ahhoz, hogy egész gyököket kapjunk. Ezek a feladatunk triviális megoldásai, amelyekből végtelen sok van, és nem túl érdekesek a számunkra. Innentől kezdve a nemtriviális megoldásokat vizsgáljuk, vagyis feltesszük, hogy sem \(a\), sem \(b\) nem 0. Két esetet fogunk vizsgálni, ha \(\lvert a\rvert=\lvert b\rvert\), illetve, ha \(\lvert a\rvert\neq \lvert b\rvert\).
1. eset: \(\lvert a\rvert=\lvert b\rvert\), és \(a\neq 0\).
Ekkor két egyenletpárunk van, az egyik kétszer az \(x^2+ax+a=0\) egyenletből, a másik pedig az \(x^2-ax+a=0\) és az \(x^2+ax-a=0\) egyenletekből áll. Világos, hogy mindegyik egyenlet diszkriminánsának négyzetszámnak kell lennie. Az \(x^2+ax+a=0\) és az \(x^2-ax+a=0\) egyenlet diszkriminánsa közös, nevezetesen \(a^2-4a={(a-2)}^2-4\). Ezek szerint \(a^2-4a\) és \((a-2)^2\) is négyzetszámok, és a különbségük 4. Nem nehéz ellenőrizni, hogy csak akkor lehet két négyzetszám különbsége 4, ha az egyik 0, a másik pedig 4. Azt kaptuk tehát ebből az észrevételből, hogy \(a^2-4a=0\), amiből következik, hogy \(a=4\), hiszen \(a\neq 0\). Vagyis két egyenletpár jöhet szóba:
– az \(x^2+4x+4=0\), amelyik saját magával alkot párt. Gyors számolással meggyőződhetünk róla, hogy ennek tényleg egész gyökei vannak: \(x_1=x_2=2\).
– a másik pedig az \(x^2-4x+4=0\) és \(x^2+4x-4=0\) egyenletekből álló pár. Viszont a második egyenletnek nem egész számok a gyökei, azaz ebben az esetben az eredeti problémára nem kapunk megoldást.
Az \(\lvert a\rvert=\lvert b\rvert\) esetben tehát egyetlen megoldás adódott: \(a=b=4\).
2. eset: \(\lvert a\rvert\neq \lvert b\rvert\), \(a\neq 0\) és \(b\neq 0\).
Mivel \(a\) és \(b\) szerepe felcserélhető a kitűzött problémában, ezért feltehetjük, hogy \(\lvert a\rvert>\lvert b\rvert\). Legyenek az \(x^2+ax+b=0\) egyenlet gyökei \(x_1\) és \(x_2\). Természetesen egyik sem lehet 0, mert \(b\neq 0\). A Viète-formulák alapján \(x_1+x_2=-a\) és \(x_1\cdot x_2=b\). Ebből, a háromszög-egyenlőtlenség általánosítását is felhasználva azt kapjuk, hogy:
| \[\displaystyle \lvert a\rvert =\lvert x_1+x_2\rvert \le \lvert x_1\rvert+\lvert x_2\rvert\] | (1) |
| \[\displaystyle \lvert b\rvert =\lvert x_1\cdot x_2\lvert =\lvert x_1\rvert \cdot \lvert x_2\rvert.\] | (2) |
Mivel \(\lvert a\rvert>\lvert b\rvert\), ezért a következőt kapjuk:
| \[\displaystyle \lvert x_1\rvert\cdot \lvert x_2\rvert<\lvert x_1\rvert+\lvert x_2\rvert.\] | (3) |
A gyökök abszolútértékei pozitív egész számok, és azt kaptuk, hogy a szorzatuk kisebb az összegüknél. Hogyan lehetséges ez? Legyenek \(k\) és \(l\) pozitív egészek, és tegyük fel, hogy \[\displaystyle k\cdot l<k+l.\]
Az egyenlőtlenség mindkét oldalából kivonjuk a \(k+l\) kifejezést és hozzáadunk 1-et.
\[\displaystyle k\cdot l-k-l+1<1,\] \[\displaystyle (k-1)(l-1)<1.\]
Mivel \(k-1\) és \(l-1\) nemnegatív egész számok, ez csak úgy lehetséges, ha legalább az egyikük 0, tehát \(k\) vagy \(l\) egyikének 1-nek kell lennie. Ezért (3) alapján valamelyik gyök abszolútértéke biztosan 1. Mivel \(x_1\) és \(x_2\) szerepe szimmetrikus, ezért feltehető, hogy \(\lvert x_1\rvert =1\). Legyen \(\lvert x_2\rvert=n\in\mathbb{N}^+\). Ekkor (2) miatt \(\lvert b\rvert=n\) és (1) miatt \(\lvert a\rvert \le n+1\). Mivel \(\lvert a\rvert>\lvert b\rvert\), ezért \(n<\lvert x_1+x_2\rvert \le n+1\). Ebből pedig az következik, hogy \(\lvert x_1+x_2\rvert=n+1=\lvert x_1\rvert+\lvert x_2\rvert\). Ha két, 0-tól különböző szám összegének abszolútértéke megegyezik az abszolútértékük összegével, akkor a két szám azonos előjelű. Tehát \(x_1\) és \(x_2\) azonos előjelűek, ezért \(b>0\), tehát \(b=n\).
Innentől két esetet különböztetünk meg attól függően, hogy \(a\) pozitív vagy negatív.
a) \(a>0\). Ekkor \(x_1+x_2=-a\) miatt a két gyök összege negatív, és mivel azonos előjelűek, ezért mindkettő negatív. Tehát \(x_1=-1\) és \(x_2=-n\), így a Viète-formulák alapján \(a=n+1\) és \(b=n\). Most tekintsük a kiindulási \(x^2+ax+b=0\) egyenlet párját, azaz az \(x^2+bx+a=0\) egyenletet. Ennek diszkriminánsa: \[\displaystyle D=\ b^2-4a=\ n^2-4(n+1)=\ n^2-4n-4={\left(n-2\right)}^2-8.\]
Az egész gyökök miatt \(D\)-nek négyzetszámnak kell lennie, és mivel \((n-2)^2\) is négyzetszám, ezért két olyan négyzetszámot keresünk, amelyek különbsége 8. Nem nehéz ellenőrizni, hogy csak akkor lehet két négyzetszám különbsége 8, ha az egyik 1, a másik 9. Ezek szerint \((n-2)^2=9\), amiből következik, hogy \(n=5\), mert \(n\) pozitív. Tehát \(b=5\) és \(a=6\), vagyis ebben az esetben egyetlen megoldás adódott, a cikk elején is említett \(x^2+5x+6=0\) és az \(x^2+6x+5=0\) másodfokú egyenletpár.
b) \(a<0\). Ekkor \(x_1+x_2=-a\) miatt mindkét gyök pozitív, ezért \(x_1=1\) és \(x_2=n\), valamint \(a=-n-1\) és \(b=n\). Az \(x^2+ax+b=0\) egyenlet párjának, vagyis az \(x^2+bx+a=0\) egyenletnek a diszkriminánsa: \[\displaystyle b^2-4a=n^2-4(-n-1)=n^2+4n+4={(n+2)}^2.\]
Az \(x^2+ax+b=0\) egyenlet diszkriminánsa pedig: \[\displaystyle a^2-4b={(-n-1)}^2-4n=n^2-2n+1={(n-1)}^2.\]
Látható, hogy mindkét egyenlet diszkriminánsa négyzetszám. Mivel a megoldóképletben szereplő számláló két tagjának paritása megegyezik, ezért ha 2-vel osztjuk, egész számokat kapunk, tehát egész számok lesznek a gyökei mindkét egyenletnek. Vagyis ebben az esetben végtelen sok, a feltételeknek megfelelő másodfokú egyenletpár létezik, hiszen \(n\) tetszőleges pozitív egész szám lehet.
Összefoglalva: a cikkben kitűzött feladat nemtriviális megoldásai a következők:
– Az \(x^2+4x+4=0\) egyenlet, amelynek a párja önmaga.
– Az \(x^2+5x+6=0\) és az \(x^2+6x+5=0\) másodfokú egyenletpár.
– Az \(x^2+(-n-1)x+n=0\) és az \(x^2+nx-n-1=0\) másodfokú egyenletpárok, ahol \(n\) pozitív egész szám. Ebbe a kategóriába tartozik a cikk elején említett \(x^2-8x+7=0\) és \(x^2+7x-8=0\) egyenletpár.
Beláttuk tehát, hogy végtelen sok nemtriviális megoldása van a cikkben kitűzött problémának, és egyúttal a Viète-formulákra is találtunk egy szép alkalmazást.
Tritz Árpád,
SZTE Báthory István Gimnázium és Általános Iskola