− a Héttusa 65. feladatának nyomában
Bevezetés
A Lyndon-szavak olyan karakterláncok egy rendezett ábécén, amelyek lexikografikus rendezésben az összes szóvégződésüket megelőzik. Egyszerű kombinatorikus definíciójuk ellenére meglepően gazdag szerkezetet hordoznak: minden szó egyértelműen felbontható Lyndon-szavak rendezett szorzatára, ami különösen alkalmassá teszi őket „építőköveknek” bonyolult algebrai és kombinatorikus objektumokban. Roger Lyndon eredetileg a szabad Lie-algebrák bázisainak előállítására vezette be őket mint „standard” sorozatokat, azóta számos más területen is alapvető szerepet kaptak. Felbukkannak az algebra, számelmélet és topológia különféle kérdéseiben, és megjelennek egészen távoli alkalmazási területeken: a számítástudománytól és kriptográfiától kezdve az elméleti fizikán és zenetudományon át egészen a molekuláris biológiáig.
A feladat
A Héttusa rovat 65. feladata – kézenfekvő általánosítással – azt kérdezte, hogy ha adott a síkon \(2m+1\) különböző pont, amelyek közül \(2m\) egy egyenesre esik, akkor azok között a háromszögek között, amelyeknek csúcsait ezen pontok közül választjuk, legfeljebb hány egyenlő szárú háromszög lehet? Könnyen beláthatjuk, hogy legfeljebb \(m\) szimmetrikus háromszög alapja illeszkedhet az egyenesre, és legfeljebb \(2m\)-nek az alapja lehet az egyenessel hajlásszöget bezáró helyzetben, így a kiválasztható szimmetrikus háromszögek száma legfeljebb \(3m\). Ahhoz, hogy ezt az értéket elérjük, a pontok az egyenesen szimmetrikus halmazt kell alkossanak, tehát az egyenesen kívüli \(O\) pontból húzott \(2m\) szakasz \(m\) különböző hajlásszöget hoz létre.
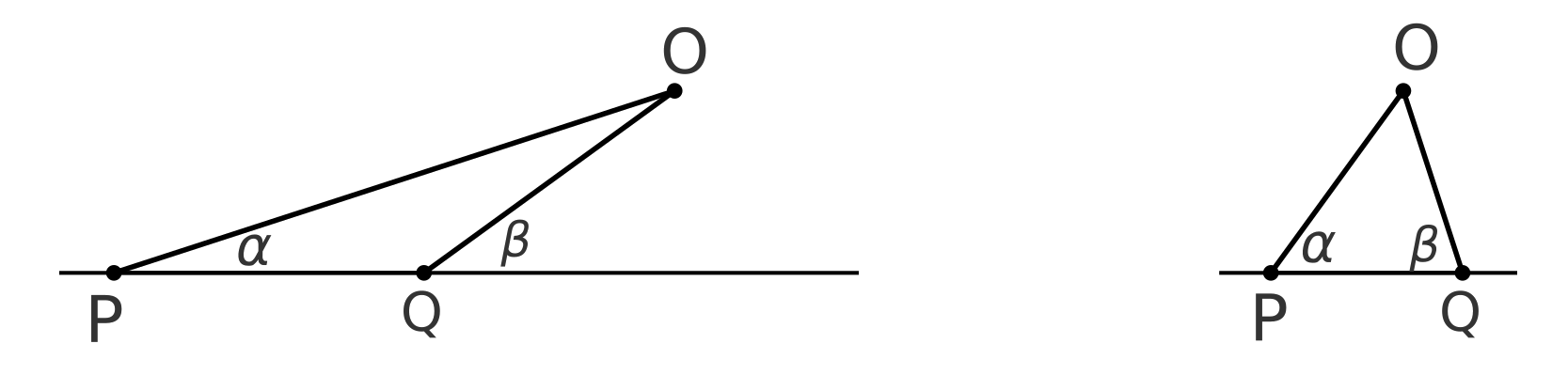
Tehát amennyiben valamennyi \(P\) ponthoz tartozik egy \(OP\) alapú egyenlő szárú háromszög, akkor az \(OP\) hegyesszögek olyan \(m\) elemű \(S\) számhalmazt alkotnak, amelyre \[\alpha\in S \quad\Longrightarrow\quad 2\alpha\in S\quad\text{ vagy}\quad \pi-2\alpha\in S.\]
A hajlásszögekre két lehetőség valamelyike teljesül. Ha a \(P\)-nél levő \(\alpha\) szög \(\pi/4\)-nél kisebb, akkor az \(OP\) alapú egyenlő szárú – tompaszögű – háromszög \(Q\) csúcspontjánál a hajlásszög a háromszög külső szöge, tehát \(\beta=2\alpha\) (bal oldali ábra). Ha \(\alpha>\pi/4\), akkor \(\beta\) maga a szárszög, azaz \(\beta=\pi-2\alpha\) (>jobb oldali ábra). Nyilván \(\alpha\not=0\), továbbá \(\alpha=\pi/3\) sem fordulhat elő a szögek közt, hiszen azzal egyenlő oldalú háromszöget kapnánk, ami többszörösen lenne számolva.
A következőkben azt vizsgáljuk, hogy a feladatból adódó természetes korlátozással (\(\alpha\not=\pi/3\)) hányféle ilyen számhalmaz létezik. A válasz egyúttal megadja azt is, hogy az eredeti geometriai kérdésre hányféle pontelrendezés szolgáltat maximális értéket.1 Mivel egyszerűbb közvetlenül a \(\pi\) szorzóit keresni, ezért az átfogalmazott kérdésünk a következő:
Hány olyan \(m\) elemű \(R\subset(0,\frac12)\setminus \{\frac13\}\) halmaz van, amelynek elemeire teljesül, hogy \(r\in R\) esetén vagy \(2r\in R\), vagy \(1-2r\in R\)?
Jelöljük az ilyen tulajdonságú halmazok számát \(a_m\)-mel. Természetesen \(a_1=0\), és \(a_2=1\), mert \(m=2\)-re az egyetlen jó halmaz \(R=\{\frac15,\frac25\}\). Az \(m=3\) eset négy megfelelő halmazát még próbálkozással megkereshetjük, hiszen a nevező rögzítése után a számláló (\(2x\) vagy \(N-2x\)) figyelése a tízes számkörben marad: \[\displaystyle\Bigl\{\frac17,\frac27,\frac37\Bigl\},\qquad \Bigl\{\frac19,\frac29,\frac49\Bigl\},\qquad \Bigl\{\frac1{10},\frac2{10},\frac4{10}\Bigl\},\qquad \Bigl\{\frac2{10},\frac3{10},\frac4{10}\Bigl\}\,.\]
Vezessük be a \(D(x)=2x\) ,,duplázó” és \(T(x)=1-2x\) ,,tükrözve duplázó” függvényeket, és a \[\Lambda(x)=\cases{D(x),&ha \(0<x<1/4,\)\\[.8em] T(x), &ha \(1/4<x<1/2\)}\] függvényt (ami \(\Lambda(x)=\frac12-|2x-\frac12|\) vagy \(\Lambda(x)=\min\{2x,1-2x\}\) alakban is írható). Így a \(\Lambda(R)\subseteq R\) tulajdonságú \(R\) halmazokat kell megkeresni. Érdemes a \(\Lambda: R\to R\) leképezés hatását irányított gráffal szemléltetni, ahol az \(r\to s\) él jelenti azt, hogy \(\Lambda(r)=s\). Ebben a gráfban minden pont kifoka 1, és minden pont befoka legfeljebb 2. Abból a célból, hogy a leképezést pontosan követni tudjuk, meg kell különböztetnünk az éleket aszerint, hogy \(\Lambda\) melyik ága viszi az él kezdőpontját a végpontba. Ezt a \(D\) vagy \(T\) betűvel fogjuk jelölni. Mivel mindkét ág invertálható, ezért ha a gráfban két irányított él ugyanabba a csúcsba érkezik, akkor egyikük \(D\), másikuk \(T\) jelzésű lesz. (Emlékezve a feladat geometriai hátterére, a hozzárendelést tekinthetjük annak, ami az \(OP\) alappal rendelkező egyenlő szárú háromszög alapjához rendeli hozzá a háromszög \(OQ\) szárát. Ha a \(Q\) pont azonos félegyenesen marad, azt a \(D\), ha a túlsó félegyenesre kerül, azt a \(T\) címke jelzi.)
Minthogy \(R\) véges, a gráfunkban mindig van ciklus (irányított kör), sőt valamivel több is igaz: minden összefüggő komponens ciklusban végződik. A függvénytulajdonságból adódik, hogy több ciklus esetén a ciklusok diszjunktak. Könnyen belátható, hogy minden címkézett ciklus – ha létezik – egyértelműen meghatározza az elemeit. Egyelemű ciklus nincs, mert \(\Lambda\) fixpontját, az \(1/3\)-ot kizártuk. Kételemű \(p\mathrel{\displaystyle\mathop{\to}^D} q\mathrel{\displaystyle\mathop{\to}^T} p\) ciklus azt jelenti, hogy \(T(D(p))=p\), azaz \(1-4p=p\), vagyis \(p=1/5\) és \(q=2/5\). Hosszabb ciklus esetén is valamilyen \(ax+b=x\) egyenlet adódik, aminek a megoldása megadja a tekintett elemet. Egy fontos kivétel azonban már kis ciklusoknál is megfigyelhető, ugyanis nem létezik sem \(p\mathrel{\displaystyle\mathop{\to}^{D}}q\mathrel{\displaystyle\mathop{\to}^{D}} r\mathrel{\displaystyle\mathop{\to}^D} p\), sem \(p\mathrel{\displaystyle\mathop{\to}^T}q\mathrel{\displaystyle\mathop{\to}^T} r\mathrel{\displaystyle\mathop{\to}^T} p\), illetve nincs még \(p\mathrel{\displaystyle\mathop{\to}^D}q\mathrel{\displaystyle\mathop{\to}^T} r\mathrel{\displaystyle\mathop{\to}^D} s\mathrel{\displaystyle\mathop{\to}^T p}\) alakú ciklus sem.
Bináris Lyndon-szavak
A feladatban felmerült címkézett ciklusok pontosan megfeleltethetők a nemtriviális bináris Lyndon-szavaknak, ezért összefoglaljuk az ezekkel kapcsolatos alapvető fogalmakat és tételeket. A 0 és 1 elemekből álló véges sorozatokat bináris szavaknak nevezzük, az \(x\) szó hosszát \(\ell(x)\)-szel jelöljük. A szavak halmazát \(A^*\)-gal jelöljük, ahol \(A\) az ábécé, itt speciálisan kételemű: \(A=\{0,1\}\). A szavakon értelmezve van egy kézenfekvő asszociatív művelet, az egymás mellé írás (szorzás). Az \(x=uv\) szó esetén \(u\)-t prefixnek, \(v\)-t szuffixnek, a \(vu\) szót konjugált szónak mondjuk. A szavak közötti lexikografikus rendezésben \(u\) megelőzi \(v\)-t, ha vagy (i) \(u\) prefixe \(v\)-nek, vagy (ii) van olyan \(r\) szó, hogy \(r0\) prefixe \(u\)-nak és \(r1\) prefixe \(v\)-nek (balról az első eltérő betű a nagyobbik szóban nagyobb). A definícióból következik, hogy a lexikografikus rendezés
(i) teljes, tehát vagy \(u\le v\), vagy \(u>v\);
(ii) ha \(u<v\), akkor tetszőleges \(x\) szó esetén \(xu<xv\); valamint
(iii) ha \(u<v\) és \(u\) nem prefix \(v\)-ben, akkor \(ux<v\).
Mivel a feladatban az egyelemű ciklusoktól el kell tekinteni, ezért a szavakat célszerű korlátozni 0-val kezdődő és 1-gyel végződőekre. Jelölje \(A_n^{01}\) a 0-val kezdődő és 1-re végződő, \(n\) hosszú bináris szavak halmazát, így tehát \(|A_n^{01}|=2^{n-2}\).
Definíció. Az \(x\in A_n^{01}\) szót Lyndon-szónak nevezzük, ha minden valódi szuffixénél kisebb, azaz minden \(x=uv\), \(u\not=\emptyset\) felbontás esetén \(x<v\).
Állítás. Ha \(x\) Lyndon-tulajdonságú, akkor
(a) \(x\) kisebb minden konjugáltjánál;
(b) \(x\) nem periodikus, azaz nincs olyan \(w\) szó, amelyre \(n\ge2\) mellett \(x=w^n\) teljesülne;
(c) ha \(y>x\) Lyndon-tulajdonságú szó, akkor \(xy\) is Lyndon-tulajdonságú.
Bizonyítás. (a) Ez a tulajdonság definíció szerint teljesül, hiszen ha \(x=uv\), akkor \(x<v<vu\).
(b) Teljesen hasonló okból, ha \(x\) Lyndon-szó, akkor semmilyen nemüres szó nem lehet egyszerre prefix és szuffix is \(x\)-ben, mivel \(x=uyu\)-ból \(x<u<x\) következne.
Megjegyzések. A (b) alatti tulajdonsággal rendelkező szavakat szokás primitív szavaknak is nevezni. Megmutatható, hogy az (a) tulajdonság jellemzi is a Lyndon-szavakat, ami így azt jelenti, hogy minden primitív szó alkalmas (azaz legkisebb) konjugáltja Lyndon-szó. Ez rögtön mutatja a feladattal való kapcsolatot. Szemléletesen, ha olyan, fehér (\(=0\)) és fekete (\(=1\)) gyöngyökből álló nyakláncot képzelünk, amelyik nem ismétel periodikusan egy mintát, akkor a nyakláncon van egy jól meghatározott hely, ahol elvágva az elvágott lánc lexikografikus rendezésben a legkisebb lenne: ott, ahonnan a leghosszabb fehér sor indul, ha több ilyen hely van, akkor ahonnan nézve az első fekete gyöngy utáni – esetleg üres – leghosszabb fehér sor indul stb. A hely éppen az aperiodikusság miatt egyértelmű. Az így kapott lánc (azaz Lyndon-szó) feleltethető meg a két színnel színezett ciklusnak.
A Lyndon-felbontás alaptétele
Állítás. Minden \(x\in A_n^{01}\) egyértelműen írható fel monoton csökkenő Lyndon-szavak szorzataként.
Bizonyítás. A létezés a szóhosszra vonatkozó teljes indukcióval bizonyítható. Ha \(x\) Lyndon-szó, akkor a felírása önmaga. Ha nem, akkor legyen \(f_1\) a leghosszabb Lyndon-tulajdonságú prefix (ilyen prefix van, legkorábban az első 0 futam végén), és legyen az \(x=f_1 y\) felírásban \(y\)-nak a feltevés szerint létező faktorizációja \(y=g_1\ldots g_k\), ahol \(g_1\ge \ldots \ge g_k\). Ekkor \(f_1\ge g_1\), máskülönben a fenti (c) tulajdonság miatt \(f_1g_1\) is Lyndon-szó lenne, ami ellentmondana \(f_1\) választásának. Így \(x=f_1 g_1 g_2\ldots\) az állításnak megfelelő Lyndon-felbontás.
Tegyük most fel, hogy \(x\)-nek kétféle felírása van, \(x=f_1f_2\ldots f_k\) és \(x=g_1g_2\ldots g_l\). Belátjuk, hogy \(f_1=g_1\). Ebből a faktorok számára vonatkozó indukcióval következni fog az egyértelműség, hiszen egytényezős faktorizáció, azaz egy Lyndon-szó biztosan nem bontható fel csökkenő tényezők szorzatára, mert definíció szerint minden szuffixánál kisebb. Ha \(f_1\not= g_1\), akkor feltehetjük, hogy \(\ell(f_1)>\ell(g_1)\). Legyen \(j\ge2\) az első index, amikor a \(g_1g_2\ldots g_j\) kezdőlánc átlépi \(f_1\) határát, azaz \(\sum_{i=1}^{j-1}\ell(g_i)<\ell(f_1)<\sum_{i=1}^{j}\ell(g_i)\). Ez valódi átlépés, különben \(f_1\) a \(g_i\)-kel faktorizálható lenne. Legyen \(h\) az \(f_1\) végén átlépett rész, azaz \(g_j\) és \(f_1\) közös része: \(g_j\)-nek prefixe és \(f_1\)-nek szuffixe. Erre a \(h\)-ra körkörös rendezés adódna, hiszen \(h< g_j\le g_1< f_1 <h\).□
Az állításból közvetlenül következik, hogy a \(\sum_{i=1}^k \ell(f_i)=n\) \((n\ge2)\) összhosszúságú, monoton csökkenő \(\{f_1\ge f_2\ge \ldots \ge f_k\}\) Lyndon-szavakból álló sorozatok száma \(|A_n^{01}|=2^{n-2}\).
Az ismétlődés nélküli faktorizációk száma
Mivel a feladathoz rendelt gráfban a ciklusok címkézése egyértelműen meghatározza a csúcsokhoz tartozó számokat, ezért a gráfban nem lehet két azonos címkézésű ciklus. Ennek megfelelően a faktorizációk között az adott összhosszúságú, csupa különböző Lyndon-szót tartalmazókat keressük. Számelméleti analógiával nevezhetnénk ezeket négyzetmentes alakoknak, ez azonban félrevezető lenne, mert a \(01001^2=01\cdot 00101\cdot 001\) példa mutatja, hogy egy szó négyzetének lehet csupa különböző Lyndon-faktora.
Jelöljük az ismétlődő Lyndon-faktor nélküli, azaz szigorúan monoton faktorizációval rendelkező \(A_n^{01}\)-beli szavak számát \(s_n\)-nel. Tetszőleges \(w\in A_n^{01}\) szó esetén építsük fel a szóban előforduló faktorokból a \((w’,w'{}’)\) párt, ahol \(w’\) a \(w\) faktorizációjában páratlan kitevővel szereplő faktorokat tartalmazza, mindet egyszeres multiplicitással, \(w”\) pedig a maradék összes többit. Így \(w'{}’\)-ben minden faktor páros sokszor fog szerepelni, hiszen a páros multiplicitású faktorok ,,ottmaradtak”, a páratlanokból pedig \(w’\)-be ,,csíptünk le” egyet. Ha így \(\ell(w'{}’)=2r\), akkor
- az összes ilyen \(w'{}’\) szavak száma \(2^{r-2}\), hisz az \(r\) összhosszúságú ,,félrészek” és a lehetséges \(r\) hosszú, \(A_n^{01}\)-beli szavak között a faktorizáció egy-egyértelmű megfeleltetést hoz létre;
- \(\ell(w’)=n-2r\) miatt az ismétlődő faktor nélküli \(w’\) szavak száma definíció szerint \(s_{n-2r}\).
Adott \(r\) mellett a lehetséges \((w’,w'{}’)\) párok száma tehát \(2^{r-2}s_{n-2r}\). Így a többszörös faktort tartalmazó \(w\in A_n^{01}\) szavak számát megkapjuk, ha ezeket összegezzük, amint \(r\) végigfut az \(r>0\) megengedett értékein, azaz \(r=2,3,\ldots, [n/2]\) (\(r\not=1\) az egyelemű faktorok tiltása miatt):
| \(\displaystyle 2^{n-2}- s_{n} = 2^0 s_{n-4} + 2^1s_{n-6} + 2^2 s_{n-8} +\ldots\) | \((1)\) |
(1)-et \(n+2\)-re is felírva:
| \(2^{n} – s_{n+2} = s_{n-2} + \big(2^1 s_{n-4} +2^2 s_{n-6} + 2^3 s_{n-8} +\ldots\big)\) | \((2)\) |
(1) mindkét oldalát 2-vel szorozva látható, hogy a (2)-ben zárójelezett rész éppen \(2^{n-1}-2s_n\)-nel egyenlő, ezt behelyettesítve azt kapjuk, hogy \(2^{n} = s_{n+2} + s_{n-2} + 2^{n-1}-2s_n\), azaz
| \((s_{n+2} -s_n) – (s_n – s_{n-2}) =2^{n-1}\,.\) | \((3)\) |
Itt a bal oldalak a szóba jövő indexekre összegezve teleszkopikus összeget adnak, amiből \[s_{n+2} – s_n = 2^{n-1} + 2^{n-3} + \ldots+2.\] Az összegzést páros és páratlan \(n\) esetén is \(s_4-s_2=s_3-s_1=2\)-vel indíthatjuk, emiatt páratlan \(n\)-re a jobb oldali mértani sorozat \(1+4+16+\ldots\) helyett \(2+4+16+\ldots\) módon kezdődik, azaz ott az összegképlet 1-gyel növelendő, tehát \[s_{n+2}-s_n=\cases{ 2^{n-1}+2^{n-3}+\ldots + 8 + 2 =(2^{n+1}-2)/3,&ha \(n\) páros,\\[0.8em] 1+2^{n-1}+2^{n-3}+\ldots + 4 + 1 = 1+(2^{n+1}-1)/3=(2^{n+1}+2)/3,&ha \(n\) páratlan, }\] ami összevont alakban
| \(d_n=s_{n+2}-s_n=\frac{2^{n+1} +(-1)^{n+1}\cdot 2}3\,.\) | \((4)\) |
Egyszerű számolás mutatja, hogy erre a \(d_n\) sorozatra\[\displaystyle\begin{align} d_n &= 2d_{n-3} + 3 d_{n-2},\\[0.8em] d_n &= 2d_{n-1} + (-1)^{n-1}\cdot 2,\\[0.8em] d_n &= 3\cdot 2^{n-1} – 2d_{n-1} – d_{n-2}, \end{align}\] Az első néhány \(n\)-re az \(A_n^{01}\)-beli szavaknál közvetlenül megszámolhatjuk \(s_n\) értékeit: \(s_1=0\), \(s_2=1\), \(s_3=2\), \(s_4=3\), \(s_5=8\), majd a fenti rekurziók segítségével teljes indukcióval igazolhatjuk \(s_n\)-re is a megfelelő képleteket:
| \(\displaystyle s_n\) | \(\displaystyle= 2 s_{n-3} + 3 s_{n-2},\) | \((5)\) |
| \(\displaystyle s_n\) | \(\displaystyle= 2 s_{n-1} + (-1)^{n-1}\cdot (n-3),\) | \((6)\) |
| \(\displaystyle s_n\) | \(\displaystyle= 2^{n-1} – 2s_{n-1} – s_{n-2}.\) | \((7)\) |
Nagyobb indexekre ,,papíron, kézzel” legegyszerűbben (6) alapján tudjuk folytatni a sorozatot:
| \(k\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(s_k\) | 0 | 1 | 2 | 3 | 8 | 13 | 30 | 55 | 116 | 225 | 458 | 907 | 1824 | 3637 | 7286 | 14559 |
Zárt alakot az (5) képlet szerinti lineáris homogén differenciaegyenlet megoldásával kaphatunk. A karakterisztikus polinom \(x^3-3x-2=(x-2)(x+1)^2\), tehát a megoldás általános alakja \(s_k=a2^k+(-1)^k(bk+c)\). A \(k=1,2,3\)-hoz tartozó kezdeti feltételekkel \(a=\frac29\), \(b=-\frac39\), \(c=\frac79\), tehát
| \(\displaystyle s_k=\frac29 2^k + (-1)^k \Big(-\frac39 k+ \frac79\Big) \qquad (k=1,2,\ldots).\) | \((8)\) |
Ez egyébként az (5)–(7) formulákhoz hasonlóan teljes indukcióval is könnyen igazolható a (4) képlet segítségével.2
A ciklusokon kívüli részgráfok (erdők) leszámolása
Rögzítsük a gráfban a ciklusok által lefedett csúcsok halmazát, legyen ez \(\,\Delta=\{c_1,c_2,\ldots,c_k\}\). Erről tudjuk, hogy nemüres, sőt az egyelemű ciklus kizárása miatt az elemszáma \(k\ge2\).
A \(\Gamma=V\setminus \Delta\) részgráf minden összefüggő komponense valamelyik \(c_j\) pontba érkezik. Ezek a komponensek az élek kétféle címkéje miatt bináris fáknak tekinthetők, így az \(n\) elemű aciklikus rész leszámolásához elegendő a bináris fákból álló \((B_1,B_2,\ldots,B_k)\) \(k\)-elemű rendezett sorozatokat megszámolnunk, ahol \(|B_1|+|B_2|+\ldots+|B_k|=|\Gamma|=n\). Itt \(B_j\) felel meg a \(c_j\) cikluspontba érkező – esetleg üres – komponens bináris fájának, nemüres fa esetén a ciklusba belépő él kezdőpontját véve gyökércsúcsnak. Jelöljük ezeknek a \(k\)-asoknak a számát \(t(n,k)\)-val. Belátjuk, hogy
| \(\displaystyle t(n,k)=t(n,k-1)+t(n-1,k+1).\) | \((9)\) |
Egyrészt azok a \(k\)-asok, ahol \(B_1\) üres, azonosíthatók a \((B_2,\ldots,B_k)\) \(k-1\) komponensű és szintén összesen \(n\) csúccsal rendelkező erdőkkel, ez a megfeleltetés adja (9) jobb oldalán az első tagot. Másrészt ha \(B_1\) nem üres, akkor legyen \(B_1=B’\cup B'{}’\) a \(B_1\) fában a bal és jobb oldali részfa a gyökércsúcs elhagyása után. Ekkor a \((B’, B'{}’, B_2,\ldots,B_k)\) erdő \(n-1\) csúcsot és \(k+1\) komponenst tartalmaz. A hozzárendelés a nemüres kezdőtagú \(k\)-asok és az eggyel kevesebb csúcsú \((k+1)\)-esek között egy-egyértelmű (visszafelé az első két komponens összeragasztása egy új gyökércsúccsal), ez igazolja (9) jobb oldalán a másik tagot.
A (9) alatti rekurzióval azonnal belátható, hogy
| \(\displaystyle t(n,k)={2n+k-1 \choose n} – {2n+k-1 \choose n-1}, \qquad\text{ha}\quad n>0,\) | \((10)\) |
mivel behelyettesítve \(t(n,k-1)+t(n-1,k+1)={2n+k-2 \choose n}-{2n+k-2 \choose n-1} + {2n+k-2 \choose n-1}-{2n+k-2 \choose n-2}\), és ebben az azonos előjelű tagokat összeadva éppen a bal oldalra vonatkozó kifejezést kapjuk. Természetesen a képlettől függetlenül \(n=0\) esetén az üres fákból álló sorozat miatt \(t(0,k)=1\), illetve triviálisan \(t(n,0)=0\), ha \(n>0\). A (10) alatti felírást a \({2n+k-1 \choose n-1}=\frac{n}{n+k}{2n+k-1\choose n}\) azonossággal egyszerűbb, és még \(n=0\)-ra is értelmes alakra hozhatjuk
| \(\displaystyle t(n,k)=\frac{k}{n+k}{2n+k-1 \choose n}.\) | \((11)\) |
A \(t(n,k)\) értékeket (\(n,k\le 10\)) a következő táblázat mutatja. Az elemek (9) miatt a Pascal-háromszögre emlékeztető módon képződnek, a Ny-i és ÉK-i szomszédok összegeként.
| \(n/k\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0 | 2 | 5 | 9 | 14 | 20 | 27 | 35 | 44 | 54 | 65 |
| 3 | 0 | 5 | 14 | 28 | 48 | 75 | 110 | 154 | 208 | 273 | 350 |
| 4 | 0 | 14 | 42 | 90 | 165 | 275 | 429 | 637 | 910 | 1260 | 1700 |
| 5 | 0 | 42 | 132 | 297 | 572 | 1001 | 1638 | 2548 | 3808 | 5508 | 7752 |
| 6 | 0 | 132 | 429 | 1001 | 2002 | 3640 | 6188 | 9996 | 15504 | 23256 | 33915 |
| 7 | 0 | 429 | 1430 | 3432 | 7072 | 13260 | 23256 | 38760 | 62016 | 95931 | 144210 |
| 8 | 0 | 1430 | 4862 | 11934 | 25194 | 48450 | 87210 | 149226 | 245157 | 389367 | 600875 |
| 9 | 0 | 4862 | 16796 | 41990 | 90440 | 177650 | 326876 | 572033 | 961400 | 1562275 | 2466750 |
| 10 | 0 | 16796 | 58786 | 149226 | 326876 | 653752 | 1225785 | 2187185 | 3749460 | 6216210 | 10015005 |
Végül tehát \(|V|=m=n+k\) helyettesítéssel és az \(s_k\) sorozat segítségével a feladat megoldását a következő összeg adja: \[a_m=\sum_{k=2}^m s_k \,t(n,k)=\sum_{k=2}^{m} \frac{k s_k}{m}{2m-k-1\choose m-k}\,.\]
Az \(a_m\) sorozat első néhány tagja:3
| \(m\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(a_m\) | 0 | 1 | 4 | 14 | 52 | 193 | 724 | 2734 | 10384 | 39626 | 151816 | 583600 | 2249916 | 8695681 | 33681460 | 130712086 |
Dombi Péter
Irodalom
- Allouche, J.-P., & Shallit, J. (2003). Automatic Sequences: Theory, Applications, Generalizations. Cambridge University Press.
- Berstel, J., Lauve, A., Reutenauer, C., & Saliola, F. (2008). Combinatorics on Words. CRM Monographs Series.
- Berstel, J., & Perrin, D. (2007). The Origins of Combinatorics on Words, European Journal of Combinatorics, 28(3), 996–1022. https://doi.org/10.1016/j.ejc.2005.07.019.
- Chen, K. T., Fox, R. H., Lyndon, R. C. (1958). Free Differential Calculus, IV. The Quotient Groups of the Lower Central Series, The Annals of Mathematics, 2nd Ser., 68(1) 81–95.
- Flajolet, P., Sedgewick, R. (2009). Analytic Combinatorics. Cambridge University Press.
- Lothaire, M. (Ed.) (1997). Combinatorics on Words. 2nd ed. Cambridge University Press.
- Lothaire, M. (Ed.) (2005). Applied Combinatorics on Words. Cambridge University Press.
- Lyndon, R. C. (1954). On Burnside’s Problem. Transactions of the American Mathematical Society, 77(2), 202–-215. https://doi.org/10.2307/1990868
- Mélançon, G., & Reutenauer, C. (1989). Lyndon Words, Free Algebras and Shuffles. Canadian Journal of Mathematics, 41(4), 577–591. https://doi.org/10.4153/CJM-1989-025-2
- OEIS Foundation Inc. (2025). The On-Line Encyclopedia of Integer Sequences, Published electronically at https://oeis.org
- Stanley, R. P. (2011). Enumerative Combinatorics. 2nd ed. Cambridge University Press.
Lábjegyzetek
1Ezúton szeretném megköszönni Berkó Erzsébetnek, hogy erre a kérdésre ráirányította a figyelmemet.↩︎
2Az \(s_k\) sorozat megtalálható a Sloane-féle enciklopédiában: https://oeis.org/A113954 és https://oeis.org/A103196.↩︎
3Ez a sorozat nem szerepel a Sloane-enciklopédiában.↩︎