Az Európai Kutatási Tanács (European Research Council, ERC) minden évben 4 kategóriában hirdet meg pályázatokat: a PhD-t legfeljebb 7 éve szerzett kutatók „Starting”, a legfeljebb 12 éve szerzettek „Consolidator Grant”-re pályázhatnak, míg az „Advanced Grant” kiírásában nincs ilyen időbeli korlát. A Synergy Grant pedig nagyobb lélegzetű (esetleg tudományágakon átívelő) kooperációk támogatását tűzi ki célul. A pályázatok rangját az adja, hogy összeurópai szinten is csak kevés nyertes pályázat kap támogatást, például az első három kategória egyenként évente 8–10 nyertes matematikapályázatot számlál, míg a Synergy Grant matematikából ritka, mint a fehér holló (de azért van).
A Rényi Intézet hagyományosan élen jár a részvételben ezeken a pályázatokon, és méretéhez képest magas nyerési aránnyal büszkélkedhet: az intézet – mintegy 60 határozatlan idejű szerződéssel rendelkező (tehát „tenure” pozícióban lévő) kutatójával – idén nyerte el a 12. pályázatot. A 11. nyertes pályázat után még egy fotó is készült, amelyen a nyertesek a magyar futballválogatott meggypiros mezében álltak (egy labda társaságában) – na nem futballtudásuk hangsúlyozására, hanem utalva arra, hogy így a legkönnyebb megjegyezni a 11-et. (A fotót a Rényi Intézetben Szilágyi Gergely készítette.)

2024-ben két magyar tudós kapott „Advanced Grant” támogatást, Pál Csaba a Szegedi Biológiai Központ munkatársaként, Stipsicz András pedig (pályafutása során másodszor) a Rényi Intézet képviseletében. Egy „Advanced Grant” tipikus költségvetése 2-2,5 millió euró szokott lenni, elosztva a futamidő öt évére. A kísérleti tudományokban nem nehéz elképzelni, mire lehet ekkora támogatást elkölteni, de mit tud ezzel kezdeni egy matematikus? A szokásos válasz erre az, hogy a matematikusok is műszerekkel dolgoznak, csak azok kicsit máshogy néznek ki, és máshogy működnek: ezek az eszközök kollégáik korábbi és most futó kutatásai, gondolatai, a velük való közös munka, együtt gondolkodás. Nem meglepő módon, ennek fenntartása-fejlesztése komoly anyagi hátteret kíván.

Stipsicz András korábbi pályázata lehetőséget adott arra, hogy a topológia egy napjainkban népszerű és dinamikusan fejlődő ágában, az alacsony dimenziós (legfeljebb négydimenziós tereket vizsgáló) topológiában építsen fel, tartson fenn és fejlesszen tovább egy (most már Európa-szerte elismert és megbecsült) kutatócsoportot. A második elnyert pályázat célja a csoport megszilárdítása, továbbépítése, és a társtudományokhoz való minél szorosabb és tartósabb kapcsolatok kiépítése – ami záloga lehet a csoport hosszútávú sikeres működésének.
De mit is csinál egy „alacsonydimenziós topológus” csoport? Mit tűztek ki maguk elé az elkövetkező öt évre? Mivel is akar foglalkozni a „Csomók és felületek 4-dimenzióban” című projekt? Természetesen a részletes leírásra itt nincs hely, és a lényeg megértéséhez is egy kis kirővel kell kezdenünk. Az egy- és kétdimenziós terek áttekintése, amely a matematika egy klasszikus fejezete, a 19. század végéig megtörtént. Meglepetésre, ezután az 5 vagy magasabb dimenziós terek áttekintésében értek el áttörő eredményeket a 60-as években, és Smale, Milnor, Stallings és számos más matematikus erőfeszítéseinek köszönhetően mára számos alapkérdés tisztázott. (Ez nem jelenti azt, hogy mindent értünk a „magas” dimenziókban, de megvannak a hatékony eszközeink a kérdések vizsgálatára, és egész jó a képünk a lehetőségekről.) A háromdimenziós kérdés már Poincaré-t is izgatta, 1905-ben írt cikkében fel is vetette a téma kulcskérdését, amit a 70-es években Thurston foglalt rendszerbe, majd 2002-ben Grigori Perelman orosz matematikus oldott meg.

Mint látható, a négydimenziós eset kimaradt a felsorolásból. Donaldson és Freedman 80-as években elért eredményei megmutatták, hogy a négydimenziós eset nagyon más, mint a többi – de hogy mire számítsunk, arról nem tudtak akkor mit mondani. Az eltelt évtizedekben kristályosodott ki, hogy a négydimenziós terek megértéséhez mindenképpen jól kell értenünk a bennük lévő felületeket. Azonban az is világossá vált, hogy ezek megértése nem adhatja meg a végső kulcsot – vannak olyan négydimenziós terek, amelyekben alig van érdekes felület. Az ötlet a háromdimenziós csomók elméletének kiterjesztése és beemelése a kérdésbe: ne csak a térben lévő felületeket vizsgáljuk, hanem hagyjunk el a terünkből egy kis részt (így keletkezik egy háromdimenziós perem), és tekintsük azokat a felületeket, amelyek erre a háromdimenziós peremre támaszkodnak valamilyen meghatározott (a háromdimenziós térben lévő, egydimenziós) csomó mentén. A pályázat lényege, hogy ez a kiterjesztett (csomók és felületek négydimenziós kölcsönhatására épülő) tudáshalmaz talán már mindent elmond a négydimenziós térről.
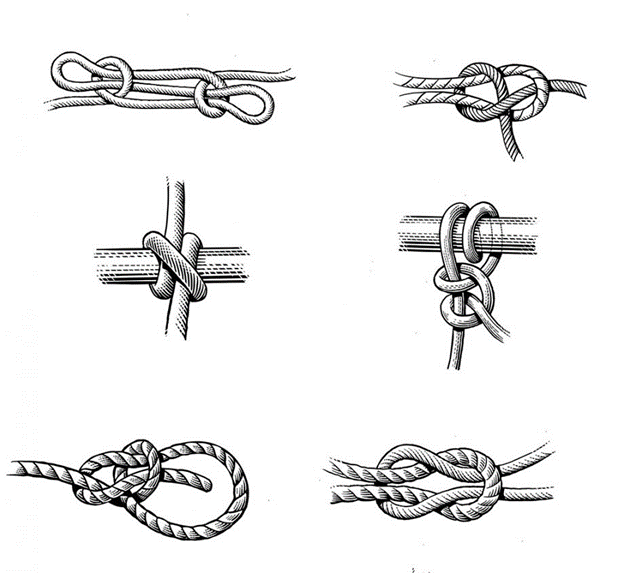
Milyen kérdéseket is vizsgál valójában egy csomóelmélettel foglalkozó matematikus (egy csomóelmélész)? Azt gondolhatnánk, a csomókról már mindent tudunk, végtére is nagyon egyszerű ezeket az objektumokat elképzelni-ábrázolni, és talán fő alkalmazási területük, hajók vitorláinak mozgatása és rögzítése már a múlt ködébe vész. Valójában a csomók kulcsszerepet játszanak a három- és négydimenziós terek ábrázolásában is – egy bonyolult, és itt nem részletezett módszer szerint – minden három- és négydimenziós (kompakt) tér lerajzolható csomók segítségével, és (elvileg) az is eldönthető, mikor reprezentálja két rajz ugyanazt a teret. Emögött az állítás mögött a Kirby-kalkulus alaptétele húzódik meg, erről Stipsicz (Robert Gompffal közösen) meghatározó monográfiát jelentetett meg a 90-es évek végén.

Visszatérve tehát a csomók elméletéhez: azt nem nehéz látni, hogy minden csomó felületet határol a háromdimenziós terünkben, és amennyiben ezt a teret valamely négydimenziós tér peremének tekintjük, a felületnek megengedhetjük, hogy a negyedik dimenzióba is behatoljon. A feladat abban áll, hogy a csomó tulajdonságaiból meg tudjuk mondani, melyik a legegyszerűbb felület, amit így a csomónkra illesztettünk. Például a háromdimenziós térben csak a triviális (nemcsomózott) csomóra tudunk körlapot illeszteni, de sokkal több csomó határol egy körlapot a standard euklideszi négydimenziós felső féltérben. (Ezen csomókat „metszet-csomóknak” nevezzük, és megismerésük központi probléma, egy általuk definiált ekvivalenciareláció a csomókat egy csoporttá teszi, amely valószínűleg a topológia egyik legbonyolultabb algebrai objektuma.)
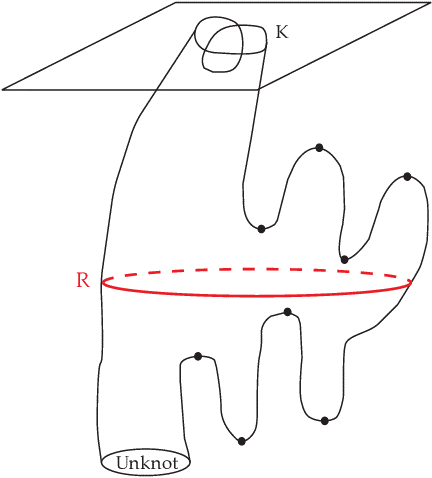
A pályázat egyik célja például annak eldöntése, hogy változó négydimenziós terekben mely csomók lesznek metszetek. Ezen tulajdonság általános feltérképezése mind a csomóelmélet, mind a négydimenziós terek elméletének előrehaladását eredményezné.
A kezdeti (egyelőre tapogatózó) kutatások már el is kezdődtek, a májusban induló csoport szeptember elsejétől teljes gőzzel és személyzettel (három doktorandusszal, egy amerikai és egy hazai posztdoktorral és három szenior kutatóval) ezt a kérdést fogja vizsgálni több szempontból és rengeteg explicit példán keresztül. A korábban írtaknak megfelelően a pályázati pénzből nem műszereket fognak beszerezni, hanem a kutatásokhoz kapcsolódó kollégákat hívnak meg rövidebb-hosszabb látogatásra, és konferenciákat terveznek a Rényi Intézeten belül működő Erdős Központ szervezésében. Ha nem is értjük meg a negyedik dimenziót teljes szépségében és komplexitásában, reméljük, hogy a pályázat zárásával sokkal közelebb érünk ehhez a régi célhoz.
Szerkesztők