Bevezetés
Amikor tárgyainkat megszámoljuk, egészen természetes módon egyesével rájuk bökünk (sorbarendezzük őket), és elmondjuk a szokásos versikét: „egy, kettő, három, …” 1. Néha, különösen hó végén a „nulla” is természetesnek tűnik. Amikor adósságba kerülünk, legtöbbször az is egész szám, és így már érthetőek a \((-2)+2=0\) és \(2\cdot(-2)=-4\) szabályok.
A kenyértörés (torta, pizza, …) feltalálása óta teljesen ésszerű (racionális) törtekről beszélni: például a torta (cserépedény) 1/6 része: 6 felé osztottuk. Ez után egészen világos, hogy ezeket a kicsi szeleteket „hatodok”-nak neveztük el, majd uzsonnástáskánkba rakva megszámoltuk, hogy 5 ilyen darabot tettünk.2
Nem tudom, hogy az ókori egyiptomi írnokok miért akartak mindent csak 1 számlálójú törtekkel felírni, például \(\dfrac{5}{6}\) helyett \(\dfrac{1}{2}+\dfrac{1}{3}\)-ot írtak. Talán kevés hely volt a drága papiruszon, mert oda csak \(\overline{2}+\overline{3}\)-t írtak. Mindenesetre jó sok fejtörést, máig megoldatlan problémát adtak a 19–21. századi matematikusoknak, bár bizonyos pizzaszeletelési feladatoknál hasznosabbak a szokásos \(\dfrac{a}{b}\) törteknél3 (lásd például [16], [19]).
Már az ókori görögök is találkoztak ezeknél bonyolultabb (valós) számokkal, pontosabban szakaszhosszúságokkal. 25 kavicsot szépen el lehet helyezni egy \(5\times 5\) -ös táblázatban, és ugyanúgy azonnal látszik, hogy egy 5 egység oldalhosszúságú négyzet egyenlő 25 kis egységnégyzettel. Az már kicsit elgondolkodtatóbb feladat, hogy 2 egységnégyzet területével mekkora oldalú, egyetlen négyzet területe egyezik meg. Erre Pitagorasz tétele adja a választ: egy egységnégyzet átlója a keresett négyzet oldala. Ezért is hívjuk ezt az átlót (szakaszt) a 2 terület gyökerének, röviden gyökének, és \(\sqrt{2}\)-vel jelöljük4, hasonlóan ahhoz, hogy a 25 terület gyökere az 5 oldalhosszúság. A térben térfogatot, vagyis köbtartalmat számolunk, és a déloszi (kockakettőzési) probléma ([17]) egy 2 köbtartalmú kocka élét keresi, vagyis \(\sqrt[3]{2}\)-t. És már meg is érkeztünk bármilyen egész gyök fogalmához: \(\sqrt[k]{m}=x\) az a keresett szám, amelyre \(x^{k}=x\cdot x\cdot\ldots\cdot x=m\) (\(k\in \mathbb{N}\), \(x,m\in \mathbb{R}^{+}\)).
Érdekességképpen megjegyezzük, hogy már Eukleidész könyvében ([2], [12]) bebizonyította, hogy bármely négyzet átlója és oldala összemérhetetlen5, vagyis hányadosuk nem racionális.
Az eddig megismert számokat elemi számolásaink (négy alapművelet, ismételt szorzás azaz hatványozás és annak megfordítása [inverze]) segítségével fedeztük fel, vagyis az algebrai műveletek segítségével. Ezért nevezték el ezeket a számokat algebrai számoknak. Talán egyetért az Olvasó abban, hogy több egyszerű, „magától értetődő” műveletet és számot nem tudunk elképzelni. A többi valódi (valós) szám jelenlegi számolási képességeinken és az algebra eszközein túli számok, vagyis transzcendens számok6. Az eddig ismertetett számok egészen egyszerűen lopták be magukat életünkbe (szívünkbe?), és érthető a folytatás:
1. definíció. Az egész számokból kiindulva, a négy alapművelettel (\(+\), \(-\), \(\cdot\), \(:\)) és az egész-gyökvonásokkal (\(\sqrt[k]{\phantom{2}}\), \(k\in \mathbb{Z}\)) felírható mennyiségeket algebrai számoknak nevezzük, a nem algebrai számok pedig transzcendensek.\(\qquad\Box\)
Például a geometriában körzővel és vonalzóval (az egységszakaszból) megszerkeszthető szakaszok mind algebraiak, hiszen itt csak négyzetgyököt kell vonnunk.
A képzetes (elképzelt7) egység \(i=\sqrt{-1}\) is algebrai, sőt a \(z=a+bi\) összetett (komplex8) szám pontosan akkor algebrai, ha \(a\) és \(b\) mindkettő algebrai. Tehát a Gauss-egészek (\(a+bi\) ahol \(a,b\in \mathbb{Z}\)), Euler- (Eisenstein-) egészek (\(a+b\rho\) ahol \(\rho=\dfrac{-1}{2}+\dfrac{\sqrt{3}}{2}i\), \(a,b\in \mathbb{Z}\)) is algebraiak. További példákat látunk még a következő fejezetben.
Könnyen belátható, hogy „mindössze” megszámlálható sok algebrai szám van (hiszen a természetes számokból kiindulva, a négy alapművelet és a \(k\)-adik gyökjelek segítségével előállított számokat szépen [végtelen] sorba tudjuk rendezni, és mind meg tudnánk számolni, ha végtelen sok időnk lenne), a valós számok halmaza pedig nem megszámlálható, hanem jóval több, kontinuum9. Tehát a legtöbb valós szám transzcendens, algebrai eszközeinken túl van.
Polinomok
Tekintsük például a következő algebrai számot: \[\label{beta} \beta=\sqrt{2}+\sqrt{5-2\sqrt{6}}-\sqrt{3}.\] Tüntessük el a gyökjeleket: \[\begin{aligned} \beta-\sqrt{5-2\sqrt{6}}&=\sqrt{2}-\sqrt{3}&&\qquad /(\phantom{2})^2\\ \beta^{2}+\left(5-2\sqrt{6}\right)-2\beta\sqrt{5-2\sqrt{6}}&=2+3-2\sqrt{6},\\ \beta^{2}&-2\beta\sqrt{5-2\sqrt{6}}=0,\\ \beta^{2}&=2\beta \sqrt{5-2\sqrt{6}}&&\qquad/(\phantom{2})^{2}\\ \beta^{4}&=4\beta^{2}\cdot\left(5-2\sqrt{6}\right)=20\beta^{2}-8\beta^{2}\sqrt{6},\\ \beta^{4}&-20\beta^{2}=-8\beta^{2}\sqrt{6}&&\qquad/(\phantom{2})^{2}\\ \beta^{8}&-40\beta^{6}+400\beta^{4}=64\cdot 6\beta^{4}\\ \beta^{8}&-40\beta^{6}+16\beta^{4}=0. \end{aligned}\]
Tehát: \(\beta\) gyöke egy egész együtthatójú10 polinomnak11! Sőt, nem túl nehéz belátni, hogy minden, egész számokból a négy alapművelettel és egész gyökökkel felírt kifejezés (szám) egy egész együtthatójú polinom gyöke!
Azonban ez fordítva sajnos nem igaz. Az Abel–Ruffini tétel12 szerint általános gyökképlet nincs 5-öd vagy magasabbfokú algebrai egyenletek (polinomok gyökei) megoldására. A helyzet azonban még ennél is „szörnyűbb”: rengeteg konkrét polinom konkrét gyökei (például \(x^{5}-4x+2\) vagy \(x^{5}-x-1\) gyökei) sem írhatók fel gyökjelekkel13 ([3], [14])!
Könnyen belátható, hogy egész együtthatójú polinomokból „csak” megszámlálhatóan végtelen van, ezért az algebra alaptétele ([13]) alapján e polinomok (valós és komplex) gyökei is „csak” megszámlálhatóan végtelen sokan vannak.
Elérkeztünk egy nagy kérdéshez: melyik legyen az algebrai számok hivatalos definíciója? A következő fejezetben válaszolunk erre pontosan.
Például mely számok gyökei egész együtthatójú polinomoknak?
A \(z=a+bi\) Gauss-számok (\(a,b\in \mathbb{Z}\)) gyökei a \(z^{2}-2az+\left(a^{2}+b^{2}\right)\) polinomnak, a \(z=a+b\rho\) Euler- (Eisenstein-) egészek (\(\rho=\dfrac{-1}{2}+\dfrac{\sqrt{3}}{2}i\), \(a,b\in \mathbb{Z}\)) gyökei a \(z^{2}+(b-2a)z+a^{2}-ab+b^{2}\) polinomnak.
Racionális \(r\) esetén a \(\cos(r\pi)\), \(\sin(r\pi)\), \(\operatorname{tg}(r\pi)\), \(\operatorname{ctg}(r\pi)\) függvényértékek (radiánban mérve!) is egész együtthatójú polinomok gyökei14 (ha értelmezettek). Például \(\cos(\pi/7)\), \(\cos(3\pi/7)\), \(\cos(5\pi/7)\) gyökei a \(8x^{3}-4x^{2}-4x+1\), \(\operatorname{tg}(3\pi/16)\), \(\operatorname{tg}(7\pi/16)\), \(\operatorname{tg}(11\pi/16)\), \(\operatorname{tg}(15\pi/16)\) pedig az \(x^{4}-4x^{3}-6x^{2}+4x+1\) polinomnak [15].
Nem egyszerű bizonyítani, de igaz: Algebrai számok összege, különbsége, szorzata, és hányadosa (sőt racionális kitevőjű hatványai is) is algebrai. Sőt: az algebrai együtthatós polinomok gyökei is algebrai számok ([7], [9], [14], [15]).
Lényeges, hogy \(\pi\), \(e\), \(\lg 2\) és még nagyon sok általunk használt szám nem algebrai ([18]). Egy érdekesség: Ha \(a\neq 0\), \(1\) és \(b\) algebrai számok, \(b\) irracionális, akkor \(a^{b}\) transzcendens (például \(\sqrt{2}^{\sqrt{2}}\)).
Most pontosan definiáljuk az algebrai számok különböző részhalmazait.
Algebrai számok
Mi most az \(\mathbb{A}\) jelet használjuk, bár sok helyen a \(\mathbb{\bar{Q}}\) jelölés használatos. \(\mathbb{Z}={}\)egész-, \(\mathbb{Q}={}\)racionális-, \(\mathbb{R}={}\)valós-, \(\mathbb{C}={}\)komplex számok halmaza. Legyen továbbá
2. definíció.
\(\mathbb{A}_{\mathbb{Z},\sqrt{\phantom{2}}}:=\left[\mathbb{Z};+,-,\cdot,\sqrt[y]{x}\right]\) azon komplex számok halmaza, amelyek felírhatók egész számok, három alapművelet (osztás nélkül) és tetszőleges „egész” (azaz \(y\in \mathbb{Z}\setminus \{0\}\)) gyökjelek segítségével,
\(\mathbb{A}_{\mathbb{Q},\sqrt{\phantom{2}}}:=\left[\mathbb{Q};+,-,\cdot,\div,\sqrt[y]{x}\right]\) azon komplex számok halmaza, amelyek felírhatók racionális számok, négy alapművelet (osztás megengedett) és tetszőleges „egész” (azaz \(y\in\mathbb{Z}\setminus\{0\}\)) gyökjelek segítségével; ezeket a számokat konstruálható számoknak is hívják,
\(\mathbb{A}_{\mathbb{Z}[x]}:=\{p(x)\text{ gyökei}\colon p(x)\in \mathbb{Z}[x], \text{főegyüttható}=\pm 1\}\) a \(\pm 1\) főegyütthatójú15, egész együtthatós polinomok (komplex) gyökeinek halmaza, e gyököket algebrai egész számoknak nevezzük, és egyszerűbben \(\mathbb{A}_{int}\)-tel jelöljük,
\(\mathbb{A}_{\mathbb{Q}[x]}:=\left\{q(x)\text{ gyökei}\colon q(x)\in \mathbb{Q}[x]\right\}\) a racionális együtthatós polinomok (komplex) gyökeinek halmaza, amely gyököket algebrai számoknak hívunk, és egyszerűen \(\mathbb{A}\)-val jelölünk.\(\qquad\Box\)
Tehát \(\mathbb{A}=\mathbb{A}_{\mathbb{Q}[x]}\) elemei az algebrai számok, és \(\mathbb{A}_{int}=\mathbb{A}\subsetneqq \mathbb{A}_{\mathbb{Q}[x]}\) elemei az algebrai egész számok.
3. megjegyzés.
i) Könnyen látható, hogy \[\mathbb{A}_{\mathbb{Q},\sqrt{\phantom{2}}}=\left[\mathbb{Z};+,-,\cdot,\div,\sqrt[y]{x}\right],\] vagyis csak egész számokból is fel tudjuk építeni a konstruálható számokat, az osztás felhasználásával.
ii) Az is nyilvánvaló, hogy bármely \(q(x)\in \mathbb{Q}[x]\) racionális együtthatójú polinomot az együtthatók nevezőinek \(c\) legkisebb többszörösével szorozva a kapott \(p(x)=c\cdot q(x)\) polinom már egész együtthatójú, vagyis \(\mathbb{Z}[x]\)-nek eleme. Ez azt jelenti, hogy a \(\mathbb{Q}[x]\)-beli polinomok gyökeinek halmaza megegyezik a \(\mathbb{Z}[x]\)-beli polinomok gyökeinek halmazával:
\[\mathbb{A}_{\mathbb{Q}[x]}=\{p(x)\text{ gyökei}\colon p(x)\in \mathbb{Z}[x] \text{ (bármilyen főegyüttható)}\}\].
A lényeges különbség \(\mathbb{A}_{\mathbb{Q}[x]}\) és \(\mathbb{A}_{\mathbb{Z}[x]}\) között az, hogy az \(\mathbb{A}_{\mathbb{Z}[x]}\)-beli (egész együtthatójú) polinomok főegyütthatójáról megköveteljük, hogy pontosan \(\pm1\) legyen. Később látni fogjuk, hogy ez nem öncélú megkülönböztetés. Az olyan polinomokat, amelyek főegyütthatója éppen \(\pm1\), angolul monic polinomoknak nevezzük.
A fentiek szerint \(\mathbb{A}_{\mathbb{Z}[x]}\subsetneqq \mathbb{A}_{\mathbb{Q}[x]}\) (lásd még az 4. Tételt), és a bevezetésben említett \(\beta\) szám \(\mathbb{A}_{\mathbb{Z}[x]}\)-nak eleme. Továbbá, a [14] és [15] honlapokon bőséges listákat találunk \(\mathbb{A}_{\mathbb{Z}[x]}\) és \(\mathbb{A}_{\mathbb{Q}[x]}\) elemeiről (algebrai és algebrai egész számokról), valamint \(\mathbb{A}_{\mathbb{Q}[x]}\)-ba nem tartozó számokról. Például, bármely \(r\in\mathbb{Q}\) racionális számra \(\sin(r\pi)\) és \(\cos(r\pi)\) is algebrai számok (elemei \(\mathbb{A}_{\mathbb{Q}[x]}\)-nak).
iii) A fent definiált \(\mathbb{A}_{\mathbb{Q},\sqrt{\phantom{2}}}\) „konstruálható” számok halmaza nem azonos a „kiszámítható”, vagy más néven „rekurzív” számok \(\mathbb{K}\) halmazával. Ez utóbbi olyan valós számokat tartalmaz, amelyek valamely algoritmussal (számítógépes programmal) tetszőleges pontossággal megadhatóak. Például \(\pi\) és \(e\) rekurzív, de nem konstruálható számok, és nyilván \(\mathbb{A}_{\mathbb{Q},\sqrt{\phantom{2}}}\subsetneqq\mathbb{K}\).
4. tétel.
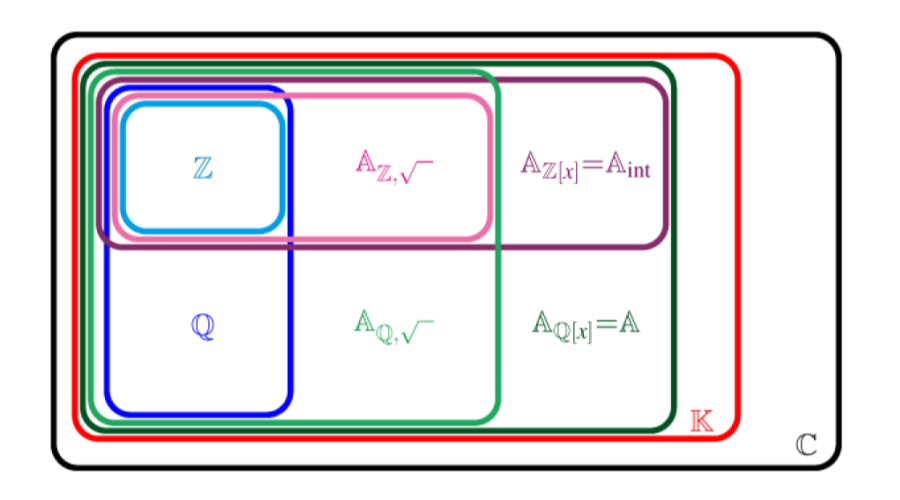
i) \(\mathbb{Z\subsetneqq A}_{\mathbb{Z},\sqrt{\phantom{2}}}\subsetneqq \mathbb{A}_{\mathbb{Z}[x]}\subsetneqq\mathbb{A}_{\mathbb{Q}[x]}=\mathbb{A}\subsetneqq\mathbb{K}\subsetneqq\mathbb{C}\),
ii) \(\mathbb{A}_{\mathbb{Z},\sqrt{\phantom{2}}}\subsetneqq\mathbb{A}_{\mathbb{Q},\sqrt{\phantom{2}}}\subsetneqq \mathbb{A}_{\mathbb{Q}[x]}=\mathbb{A}\),
iii) \(\mathbb{Z}\), \(\mathbb{A}_{\mathbb{Z},\sqrt{\phantom{2}}}\) és \(\mathbb{A}_{\mathbb{Z}[x]}\) gyűrűk (azaz zártak az összeadásra, kivonásra és szorzásra),
iv) \(\mathbb{Q}\), \(\mathbb{A}_{\mathbb{Q},\sqrt{\phantom{2}}}\), \(\mathbb{A}_{\mathbb{Q}[x]}\) és \(\mathbb{K}\) testek (azaz zártak a négy alapműveletre).\(\qquad\Box\)
5. megjegyzés. A fenti i) és ii) összefüggéseket az alábbi ábra szemlélteti, bár azt nem tükrözi, hogy ugyan mindegyik \(\mathbb{A}_{\ast}\) halmaz és \(\mathbb{K}\) is megszámlálhatóak (vagyis ugyanannyi elemük van, mint \(\mathbb{N}\)-nek), \(\mathbb{C}\) viszont kontinuum számosságú.

Alkalmazások
Most csak azon alkalmazásokat említjük meg, amelyek a szerző szívéhez közel állnak, sorrend nélkül.
Közelítő számítások
Napjainkban a numerikus (közelítő) számítások előtérbe kerülnek az elméleti „pontos” megoldásokkal szemben. Az algebrai számok hiába vannak mindenütt sűrűn a valós számegyenesen (bármely kis intervallumban végtelen sok algebrai szám van), de van „bonyolultságuk”, hasonlóan az irreducibilis tört számok16 nevezőjéhez. Például, ha az \(\dfrac{x}{n}\) és \(\dfrac{y}{n}\) számok közelítő alakjából szeretnénk eldönteni a két szám egyenlőségét, akkor ezt az \(\dfrac{x}{n}\) és \(\dfrac{y}{n}\) számok kb. \(\dfrac{1}{2n}\)-nél pontosabb kiszámításával el tudjuk dönteni.
A törtek nevezőihez hasonlóan az algebrai számoknak (egész együtthatós polinomok gyökeinek) is van „bonyolultsága” ([7]), ami alapján például egyenletek gyökeinek közelítő értékeiből is meg lehet határozni a gyökök azonosságát vagy különbözőségét.
Például, szokásos középiskolai átalakításokkal belátható, hogy \(\sqrt{2}+\sqrt{5-2\sqrt{6}}=\sqrt{3}\), azaz az (1)-ben említett szám esetében \(\beta=0\). A diákok kedvenc módszere a tanár bosszantására: „kiszámoltam zsebszámológéppel, és nulla”. Nos, mivel \(\beta\) „bonyolultsága” legalább \((16{,}22)\), ezért \(\lvert \beta \rvert \leq 6{,}3\cdot 10^{-39}\), vagyis elég egy olyan számológép, amely legalább 41 tizedesjegy pontossággal tud számolni! Ha ennyi tizedesjegy valóban 0, akkor \(\beta=0\) valóban, egzakt matematikai értelemben, nemcsak numerikus közelítéssel! (Részletek például az [7] és [9] cikkekben találhatók.)
Egy másik alkalmazást az [1] cikkben ismerhetünk meg közelebbről: Bozóki Sándor, Tsung-Lin Lee és Rónyai Lajos hasonló módszerrel igazolták John Edensor Littlewood 1968-ban megjelent sejtését: lehetséges hét (elegendően hosszú) azonos átmérőjű hengert elhelyezni a térben úgy, hogy mindegyik érintse mindegyiket. (Érdemes még elolvasni Grätzer József [4] könyvének 115. és 233. oldalait.)
Rugalmas pénzérmék
Ha feldobunk kétszer egy olyan pénzérmét, amely \(p_{3}=\dfrac{3+\sqrt{3}}{6}\) valószínűséggel fej és \(1-p_{3}=\dfrac{3-\sqrt{3}}{6}\) valószínűséggel írás, akkor annak a valószínűsége, hogy egy írást és egy fejet dobunk: \[P_{\circ\bullet,\bullet\circ}=2p_{3}(1-p_{3})=2\cdot\dfrac{3+\sqrt{3}}{6}\cdot\dfrac{3-\sqrt{3}}{6}=\dfrac{1}{3},\] míg háromszor feldobva ugyanezt az érmét, annak a valószínűsége, hogy három írást vagy három fejet dobunk: \[P_{\circ\circ\circ,\bullet\bullet\bullet}=p_{3}^{3}+(1-p_{3})^{3}=\left(\dfrac{3+\sqrt{3}}{6}\right)^{3}+\left(\dfrac{3-\sqrt{3}}{6}\right)^{3}=\dfrac{1}{2}.\]
Úgy is fogalmazhatunk, hogy a fenti egyetlen pénzérmével szimulálhatjuk mind a szabályos \(\dfrac{1}{2}\), \(\dfrac{1}{2}\), mind az \(\dfrac{1}{3}\), \(\dfrac{2}{3}\) valószínűségű fej-írás pénzérméket! Jelben: \(p_{3}\rightsquigarrow \dfrac{1}{2}\) és \(p_{3}\rightsquigarrow \dfrac{1}{3}\).
A „szimulálni” relációt (\(\rightsquigarrow\)) pontosan a [8] és [10] cikkekben definiáljuk, most csak egy egyszerűbb (általánosított) meghatározást adunk.
6. definíció. Tetszőleges \(p\), \(r\) valós számokra \(p\) szimulálja \(r\)-et, jelben \(p\rightsquigarrow r\), ha van olyan \(u(x)\) nemnegatív egész együtthatójú polinom, amelyre \(u(p)=r\).\(\qquad\Box\)
Nyilván, ha \(p\rightsquigarrow r,s\) akkor \(p\rightsquigarrow r+s\) és \(p\rightsquigarrow r\cdot s\).
Az igazi „artistamutatvány” az, ha egy \(p\) valós számmal egyszerre több valós számot is tudunk szimulálni (azaz \(u(p)=r\) és \(v(p)=s\) valamely \(u,v\) polinomokra)! A bevezető példában \(u(p)=2p(1-p)=2p-2p^{2}=1/3\) és \(v(p)=p^{3}+(1-p)^{3}=3p^{2}-3p+1=1/2\). [10] és [11]-ben többek között belátják a szerzők, hogy pozitív racionális számok tetszőleges véges részhalmaza mindig szimulálható egyetlen pozitív \(p\) valós számmal.
Azonban például \(\sqrt{2}\) és \(\pi\) egyszerre nem szimulálható egyazon \(p\) számmal. Ugyanis ha \(u(p)=\sqrt{2}\) valamely \(u(x)\) egész együtthatójú polinomra, akkor \(p\) algebrai. Ekkor viszont \(v(p)=\pi\) nem lehet, mert \(v(p)\) algebrai, míg \(\pi\) transzcendens.
Könnyen kijelenthetnénk, hogy \(u(p)=r\) és \(v(p)=s\) esetén \(p\), \(r\) és \(s\) „ugyanazon algebrai fokú” számok kellenek, hogy legyenek. De ennek precíz megfogalmazása és alkalmazása nagyon nehéz.
Már több, mint 30 éve megoldatlan a következő probléma:
7. probléma. \(\dfrac{1}{\sqrt{2}}\) és \(\dfrac{1}{\sqrt{3}}\) szimulálhatók-e egyszerre, azaz léteznek-e olyan \(u(x)\) és \(v(x)\) nemnegatív egész együtthatójú polinomok és olyan \(p\) valós szám, amelyekre \(u(p)=\dfrac{1}{\sqrt{2}}\) és \(v(p)=\dfrac{1}{\sqrt{3}}\)?\(\qquad\Box\)
Szalkai István
Pannon Egyetem, Veszprém
szalkai.istvan@mik.uni-pannon.hu
Irodalom
Lábjegyzetek
-
Más nyelvterületen „einz, zwei, drei,…”. De a lényeg: egy bijekciót adunk meg a tárgyak és \(\mathbb{N}=\left\{\right.\)egy, kettő, három, …\(\left.\right\}\) halmaz egy kezdő részhalmaza között.↩︎
-
Egyetemi felvételi után már nem sokan emlékeznek arra, hogy az \(\dfrac{5}{6}\) képletben \(5={}\)„(meg)számláló”, \(6={}\)„(el)nevező” és – a törésvonal (törtvonal).↩︎
-
Ha például 5 pizzát akarunk 8 személyre szétosztani, akkor a szokásos módszerrel \(5\cdot 8=40\) vágás kell. Azonban, egyiptomi törtekkel \(5/8=1/2+1/8\), ami alapján mind a 8 személy egy fél és egy nyolcad szeletet kap, vagyis 4 pizzát félbevágunk (4 vágás) és egy pizzát 8 felé (8 vágás). Tehát 40 vágás helyett 12 vágással megússza a pizzafutár ([19]).↩︎
-
A \(\sqrt{\phantom{2}}\) jel állítólag egy kézzel írt, kicsit elkapkodott r betű kiegyenesített változata, hiszen latinul (és angolul) root jelentése gyökér, mind növénytanban mind matematikában. A gyökjel neve radical (\(\Rightarrow\) radikális = gyökeres, például változás).↩︎
-
Az ókori görögök még nem használtak sem valós számokat, sem számegyenest. A természetes számok kavicsok voltak (például „háromszög-számok”), a törtek helyett szakaszok arányáról beszéltek, és legfőképpen szakaszok hosszaival foglalkoztak. Két szakaszt, \(a\) és \(b\), összemérhetőnek neveztek, ha létezik közös mértékegységük, azaz olyan \(d\) szakasz, amelyekre \(a=k\cdot d\) és \(b=\ell \cdot d\) ahol \(k\), \(\ell\) egész számok, vagyis \(a/b=k/\ell\) racionális. (\(d\) így a legnagyobb közös osztója a tetszőleges pozitív valós \(a\), \(b\) számoknak.) Tehát a \(b=1\) egységszakasszal összemérhetetlen szakaszok irracionális hosszúak.↩︎
-
transz/transzcendens = valamin túli, valamin keresztül, mint például transzformátor, „transzba esett” (valóságon túlra), Liszt Ferenc „Transzcendens etűdök” (zongorista képeségein túli zongoraművek) stb.↩︎
-
imaginare (lat) = imagine (ang) = elképzelni↩︎
-
komplex = összetett, például nyelvvizsga↩︎
-
„kontinuum” szó szerint „a folytonosság”, hiszen a valós számegyenes minden (geometriai) pontját folytonosan kitöltik a valós számok. (Lásd még „continuous” angolul, vagy „kontinuitás elve” a politikában, stb.)↩︎
-
együtt-ható = co-efficient (ang) = koefficiens (a bankban)↩︎
-
Nem tudom, miért hívják egy függvény gyökének (gyökerének) a zérushelyeit. Másod-, harmad-, negyedfokú polinomok („soktagúak”) esetében a zérushelyeket ki lehet fejezni gyökjelekkel, de magasabbfokú polinomok esetében már nem.↩︎
-
A tétel bizonyításával Bolyai János is behatóan foglalkozott.↩︎
-
Kicsit pontosabban: a fenti polinomok egyik gyökét sem lehet felírni az 1. Definíció szerint.↩︎
-
Ha fokban szeretnénk mérni, vagyis \(\cos(x^{\circ})\) és \(\sin(x^{\circ})\)-ról beszélünk, akkor racionális \(x\) esetén lesz \(\cos(x^{\circ})\) és \(\sin(x^{\circ})\) algebrai szám.↩︎
-
Egy polinom főegyütthatója a legmagasabb fokszámú tagjának együtthatója.↩︎
-
A tovább nem egyszerűsíthető törteket, vagyis amikor a számláló és a nevező relatív prímek, nevezzük irreducibilis törteknek. Minden tört (racionális szám) egyenlő pontosan egy irreducibilis törttel.↩︎