Egy \(X=(V,E)\) gráf alatt egy véges \( V\) csúcshalmazt és egy csúcspárokat tartalmazó \( E\) élhalmazt értünk. Expandernek nevezünk egy gráfot, ha az sokszorosan összefüggő ritka gráf. Ez az a látszólagos ellentmondás, miszerint egy expander sokszorosan összefüggő, ugyanakkor ritka, ami miatt az ilyen gráfok egyrészt intuíciónk ellenére léteznek, másrészt pont emiatt annyira hasznosak. Például az elméleti matematikában, ezen belül is a kombinatorikában expanderek által adható explicit konstrukció olyan gráfokra, amelyeknek egyszerre nagy a derékbősége (a gráfban található legrövidebb kör hossza) és a kromatikus száma (a legkevesebb szín, amivel a csúcsok kiszínezhetők oly módon, hogy szomszédos csúcsok színe különböző legyen); a funkcionálanalízisben pedig olyan végesen generált csoportokat konstruálhatunk a segítségükkel, amelyek nem ágyazhatók be egyenletesen Hilbert-térbe (Gromov), valamint a csoporthatásokra vonatkozó Baum-Connes-sejtésre is ellenpéldákat szolgáltatnak. Azonban az expanderek hatása leginkább a számítástudományban, illetve a számítógép-tudományban érzékelhető. Szuperhatékony kommunikációs hálózatok tervezése, hatékony hibajavító kódok konstrukciója, véletlen algoritmusok derandomizációja, valamint algoritmusok elemzése a számítógépes csoportelméletben: csupán néhany példa az expanderek széleskörű alkalmazásaira (lásd még O. Reingold…. tanulmányát és a benne szereplő további hivatkozásokat).
A legalapvetőbb expander formálisan a következőképp definiálható. Legyen \( k \geq 2\) egész szám, \( X\) pedig egy \( k\)-reguláris gráf (azaz minden \( v \in V\) csúcsnak pontosan \( k\) szomszédja van). Az \( X\) gráf \( h\) Cheeger-konstansa \[\displaystyle h(X) = \min_{\emptyset \subsetneq F \subsetneq V}\frac{\vert\partial F\vert}{\min(\vert F\vert,\vert V \setminus F\vert)},\] ahol \( \partial F\) jelöli az \( F\) és annak \( V \setminus F\) komplemense között futó élek halmazát, \( \vert\partial F\vert\) pedig annak számosságát. Ekkor \( X\)-et \([n,k,h]\)-expandernek nevezzük, ahol \( n=\vert V\vert\). Vegyük észre, hogy \( h > 0\) akkor és csakis akkor, ha \( X\) összefüggő. Továbbá ha \( \vert F\vert \leq n/2\), akkor \( \vert\partial F\vert \geq h\vert F\vert\), vagyis ha \( h\) értéke nagy, akkor a csúcsok minden ilyen \( F\) részhalmazának sok szomszédja van \( F\)-en kívül (innen az expander elnevezés). Expanderek alatt valójában ilyen \( [n,k,h]\) gráfok egy végtelen sorozatát értjük, ahol \( k\) és \( \varepsilon_o > 0\) értéke rögzített, \( h \geq \varepsilon_0\) (a sorozat mindegyik elemére), valamint \( n \rightarrow \infty\). Könnyű látni, hogy ekkor szüksgképpen \( k \geq 3\), amit ezért a továbbiakban fel is teszünk. A \( h \geq \varepsilon_0 > 0\) feltétel biztosítja, hogy a gráfok sokszorosan összefüggők, miközben \( k\) rögzített értéke (és \( \vert E\vert=kn/2\)) miatt ritkák.
Talán meglepő, hogy expanderek egyáltalán léteznek. Az első egzisztenciabizonyítást Pinsker adta. Tekintsük az összes \( X_{n,k}\) (vagyis \( n\) számozott csúcson \( k\)-reguláris) gráfok valószínűségi terét, ahol mindegyik ilyen \( X_{n,k}\) gráfot egyforma valószínűséggel választjuk. Ekkor megmutatható, hogy \( k \geq 3\) esetén létezik \( \varepsilon = \varepsilon(k) > 0\), hogy a \( h(X_{n,k}) \geq \varepsilon\) esemény valószínűsége \( 1\)-hez tart, amint \( n \rightarrow \infty\).
Az alkalmazásokhoz azonban explicit konstrukciókra van szükség. Ebből a szempontból a következő spektrális megközelítés nagyon hasznosnak bizonyult. Adott \( X = X_{n,k}\) esetén tekintsük az \( A = A(X)\) szomszédsági mátrixot: ez egy \( n \times n\)-es szimmetrikus mátrix, amelynek sorait és oszlopait a \( v \in V\) csúcsokkal címkézzük és az \( A_{v,w}\) mátrixelem értéke \(1\) ha \( \{v,w\} \in E\), máskülönben 0. Az \( (1,1,\ldots,1)\) vektor sajátvektora \( A\)-nak \( k\) sajátértékkel, továbbá \( A\) sajátértékei valósak és a \( [-k,k]\) intervallumba esnek. Jelölje \( \lambda_1(X)\) az \( A\) mátrix \( k\) után következő legnagyobb sajátértékét. Az alábbi, Tanner, Alon és Milman nevéhez fűződő egyenlőtlenségek − amelyek a differenciálgeometriában ismert Cheeger- és Buser-egyenlőtlenségek diszkrét analogonjai − kapcsolatot teremtenek \( h(X)\) és \( k-\lambda_1(X)\) (az ún. spektrális rés) között: \[\displaystyle \frac{k-\lambda_1(X)}{2} \leq h(X) \leq \sqrt{2k(k-\lambda_1(X))}.\]
Következésképp, az \( X_{n,k}\) család pontosan akkor expander, ha a spektrális résekre egyenletes alsó korlát adható, és minél nagyobb a rés, annál jobb az expanzió. Margulis ezt az eredményt, valamint a Kazhdan-féle (T)-tulajdonsággal rendelkező (ami annyit jelent, hogy a csoport triviális reprezentációja izolált az unitér reprezentációk terében) végtelen diszkrét csoportok faktorait felhasználva elsőként adott explicit konstrukciót expanderekre. Azonban van határa annak, hogy legfeljebb mekkora lehet a spektrális rés (Alon-Boppana): rögzített \( k\)-ra ugyanis \[\displaystyle \liminf_{n \rightarrow \infty} \lambda_1(X_{n,k}) \geq 2 \sqrt{k-1},\] ahol a „\( \liminf\)” képzésekor az összes \( X_{n,k}\)-t figyelembe vesszük. Egy \( X_{n,k}\) gráf (pontosabban \( X_{n,k}\)-k végtelen sorozata, ahol \( n \rightarrow \infty\) és \( k\) rögzített) Ramanujan-gráf, ha \( \lambda_1(X_{n,k})\leq 2 \sqrt{k-1}\). A fentiek tekintetében egy ilyen gráf spektrális szempontból optimális expander.
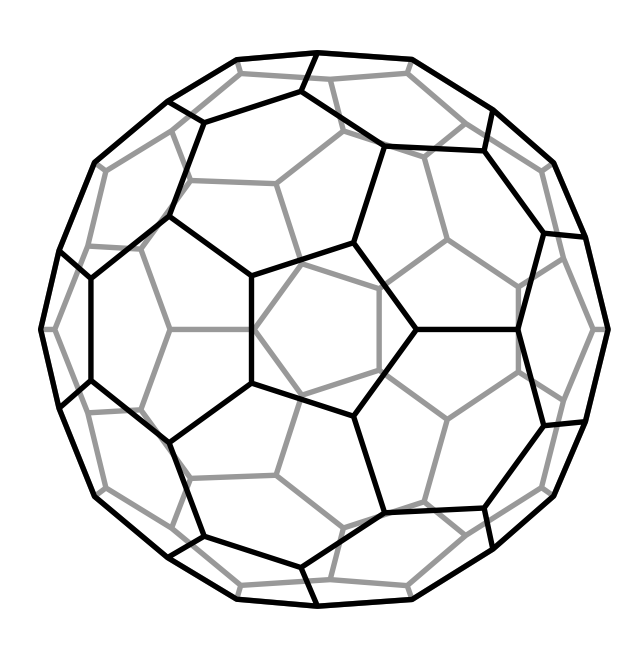
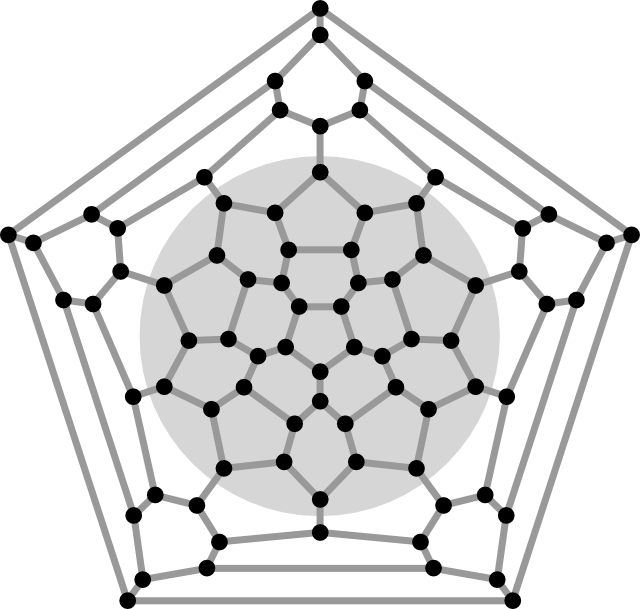
Ennek a Ramanujan-gráfnak 80 csúcsa van, amely közel van a legnagyobb, 84 csúcsú Ramanujan-síkgráfhoz. A derékbősége 5, az expanziós konstansa \(1/4\) (amint ezt az árnyékolt kör jelzi), a \(\lambda_1\) sajátértéke pedig nagyjából \(2{,}81811\dots\) (A. Gamburd számítása.)
Kellemes tény, hogy \( k=q+1\) esetén (ahol \( q\) prímhatvány) léteznek Ramanujan-gráfok, amelyek egy alkalmas véges test feletti \( PGL_2\) csoport explicite leírható Cayley-gráfjaiként nyerhetők [1, 3] (egy Cayley-gráfban a csúcsok egy adott \( G\) csoport elemeinek felelnek meg, az élek pedig \( g \rightarrow gg_1\) kapcsolatoknak, ahol \( g_1 \in G\) egy tetszőleges generátorelem). Érdekes kérdés, hogy vajon léteznek-e Ramanujan-gráfok, amennyiben \( k\) nem prímhatvány. Friedman nemrég megmutatta, hogy rögzített \( k\) és \( \varepsilon > 0\) esetén a \( \lambda_1(X_{n,k})\leq 2 \sqrt{k-1} + \varepsilon\) esemény valószínűsége 1-hez tart, amint \( n \rightarrow \infty\), vagyis egy véletlen gráf aszimptotikusan Ramanujan.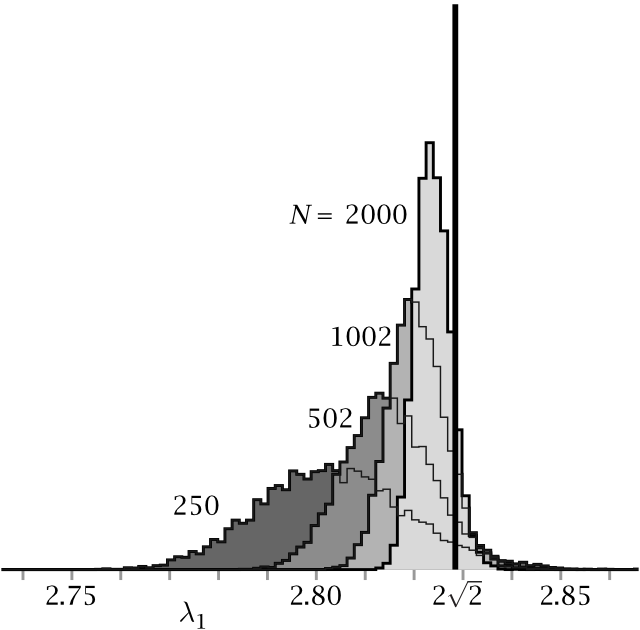
Rendkívül érdekes numerikus szimulációk alapján úgy tűnik, hogy annak valószínűsége, hogy egy véletlen gráf Ramanujan, valamivel nagyobb mint \(0{,}5\), ami a véletlen mátrixok elméletéből ismert Tracy-Widom-eloszlás ferdeségének felel meg. 3-reguláris \(N=|V|\) méretű véletlen gráfok \(\lambda_1\) sajátértékeinek gyakorisági eloszlása (az adatokat T. Novikoff bocsátotta rendelkezésre).
A [4] cikkben a szerzők bevezették gráfok „zig-zag-szorzatát” (amely csoportok szemidirekt szorzatához kapcsolódik abban az esetben, amikor maguk a gráfok Cayley-gráfok), amelynek segítségével új explicit konstrukciót adtak expanderekre. Az eljárás induktív: mindegyik szinten a zig-zag-szorzat alkalmazása kínálja a továbblépést. A konstrukció előnye, hogy segítségével „veszteségmentes expandereket” kaphatunk: olyan gráfokat, amelyek expanziója kis csúcshalmazokon közel optimális. Ez az extra csavar rendkívül hasznosnak bizonyult számos alkalmazásban, rádásul nem mutatható ki a spektrális rést elemezve.
Fordította: Huszár Kristóf
A fordítás megjelentetésére folyóiratunkban engedélyt kaptunk az Amerikai Matematikai Társulattól (AMS), a szerzőtől és az ábrák jogtulajdonosától (William A. Casselman). Peter Sarnak, “What Is…an Expander?” Notices Amer. Math. Soc.51 (August 2004) 762-763. © 2004 American Mathematical Society. http://www.ams.org/
Hivatkozások
[1] Alexander Lubotzky − Ralph Phillips − Peter Sarnak: Ramanujan graphs. Combinatorica, 8. évf (1988) 3.sz., 261–277. p.
[2] Adam Marcus − Daniel A. Spielman − Nikhil Srivastava: Interlacing families I: Bipartite Ramanujan graphs of all degrees. In 2013 IEEE 54th Annual Symposium on Fiundations of Computer Science (FOCS) (konferenciaanyag). 2013, IEEE, 529–537. p.
[3] Moshe Morgenstern: Existence and explicit construczions of q+1 regular Ramanujan graphs for every prime power q. Journal of Combinatorial Theory, Series B, 62. évf. (1994) 1.sz., 44–62. p.
[4] Omer Reingold − Salil Vadhan − Avi Wigderson: Entropy waves,the zig-zag graph product, and new constant-degree expanders. Annals of Mathematics, 1955. évf. (2002) 1.sz., 157–187. p.
A fordító megjegyzései
1Marcus, Spielman és Srivastava 2013-as áttörése óta tudjuk, hogy a válasz igenlő a cikkben feltett kérdésre, hogy vajon léteznek-e Ramanujan-gráfok, amennyiben \(k\) nem prímhatvány [2].
2T. Novikoff szimulációinak az eredeti megjelenés óta elavult a cikkbeli linkje http://www.math.nyu.edu/Courses/V63.0393/.
