Ebben a cikkben egy egyszerű kombinatorikus játékot mutatunk be, amely középiskolás szinten is megérthető, ugyanakkor gazdag és érdekes matematikai tulajdonságokkal rendelkezik, számos nyitott kérdéssel. A kivonós játékot két játékos játssza a következő szabályokkal. Adott egy pozitív egész szám, \(n\), és pozitív egész számok véges halmaza, \(A\). Elhelyezünk \(n\) db kavicsot egy asztalra, és a két játékos felváltva vesz el a kavicsokból. Minden lépésben az elvett kavicsok száma meg kell, hogy egyezzen az \(A\) halmaz valamely elemével, de ezen felül semmi további kikötés nincsen, az \(A\) halmaz bármelyik eleme akármelyik játékos által akármikor, akárhányszor választható a játék során. Ha az asztalon levő kavicsok száma kevesebb, mint az \(A\) halmaz minimuma, akkor az aktuálisan lépő játékos elveszítette a játékot, és a másik játékos nyert. Az alapkérdés az, hogy adott \(n\) és \(A\) halmaz esetén melyik játékosnak van nyerő stratégiája, azaz melyik játékos az, aki mindenképpen meg tudja nyerni a játékot, bárhogyan is játszik a másik játékos. Az olvasókat buzdítjuk arra, hogy próbálják maguk bizonyítani a következő állítást, mielőtt elolvasnák a bizonyítást.
1. Állítás. Legyen \(A=\{1,2,3,4\}\) és \(n=20\). Ekkor a második (azaz nem a kezdő) játékosnak van nyerő stratégiája.
Bizonyítás. A nyerő stratégia az, hogy minden fordulóban, ha az első játékos \(k\) kavicsot vesz el, a második játékos \(5-k\) kavicsot vesz el. Ez mindig lehetséges, hiszen az \(A\) halmaz minden lehetséges \(k\) elemére igaz az, hogy az \(A\) halmaz az \(5-k\) elemet is tartalmazza. Így az első forduló után 15 kavics marad, a második forduló után 10, a harmadik forduló után 5, a negyedik forduló után pedig 0 kavics marad, akárhogyan is játszik az első játékos. Ezután az első játékos nem tud lépni, így a második játékos nyert. □
Mi a helyzet, ha továbbra is \(A=\{1,2,3,4\}\), de \(n=23\)? Könnyen belátható, hogy ebben az esetben a kezdő játékosnak van nyerő stratégiája. Valóban, az első játékos az első lépésben 3 kavicsot vesz el. Ekkor 20 kavics marad, tehát a helyzet most megegyezik az előbbi játékkal, de most a második játékos lép először, és el fogja veszíteni a játékot, amennyiben az első játékos az előző bizonyításban leírt stratégiát követi.
Általánosan is igaz, hogy ha egy adott állásban az aktuálisan lépő játékosnak van olyan lépése, amely olyan álláshoz vezet, amelyben a második játékosnak van nyerő stratégiája, akkor az aktuális játékos meg tudja nyerni a játékot. Azonban ha minden lehetséges lépés olyan álláshoz vezet, amelyben a kezdő játékosnak van nyerő stratégiája, akkor az aktuális játékos elveszíti a játékot.
Definiáljuk az \(f_A(n)\) függvényt a következőképpen. Legyen \(f_A(n)=1\), ha n kaviccsal kezdve az első játékosnak van nyerő stratégiája abban a játékban, amelyben az elvehető kavicsok számát az \(A\) halmaz adja meg, és legyen \(f_A(n)=0\), ha a második játékosnak van nyerő stratégiája. Ekkor teljesül a
\[\displaystyle f_A(n)=1-\min\limits_{x\in A} \{f_A(n-x)\}\]
egyenlőség. Valóban, \(f_A(n)\) 1 lesz, amennyiben \(\min\limits_{x\in A} \{f_A(n-x)\}=0\), azaz van olyan \(x\in A\), hogy \(f_A(n-x)=0\), azaz az első játékos el tudja navigálni a játékot egy olyan állásba, ahonnan kezdve a második játékosnak van nyerő stratégiája. Ha azonban \(\min\limits_{x\in A} \{f_A(n-x)\}=1\), akkor \(f_A(n)\) 0 lesz, mert az első játékos bármelyik lépésére az ellenfelének lesz nyerő stratégiája.
Az olvasókat megint biztatjuk, hogy a következő állítást próbálják meg bizonyítani, mielőtt elolvasnák a bizonyítást.
2. Állítás. Bármely véges \(A\) halmazra az \(f_A(n)\) függvény időben periodikussá válik, azaz létezik olyan \(n_0\) és \(p\), hogy minden \(n\ge n_0\)-ra \(f_A(n)=f_A(n+p)\).
Bizonyítás. Legyen \(F_A\) egy, a \(\max\{A\}\) hosszúságú 0-1 vektorokat \(\max\{A\}\) hosszúságú 0-1 vektorokba képező függvény a következő hozzárendelési szabállyal. Ha \(Z=(z_0,z_1,\dots ,z_{\max\{A\}-1})\), akkor
\[\displaystyle F_A(Z)=\Bigl(z_1,z_2,\dots z_{\max\{A\}-1},1-\min\limits_{x\in A} \{z_{\max\{A\}-x}\}\Bigr).\]
Vegyük észre a következőt.
Ha \(Z_0:=(f_A(0),f_A(1),\dots ,f_A(\max\{A\}-1))\), akkor
\(Z_1:=F_A(Z_0)=(f_A(1),f_A(2),\dots ,f_A(\max\{A\}))\), és rekurzívan minden \(n\)-re
\(Z_n:=F_A(Z_{n-1})=(f_A(n),f_A(n+1),\dots ,f_A(\max\{A\}+n-1))\). Mivel \(F_A\) egy véges halmazból ugyanabba a véges halmazba képező függvény, a skatulyaelv alapján lesznek olyan \(p_1<\) \(p_2\) számok, hogy \(Z_{p_1}=Z_{p_2}\). De ekkor \(Z_{p_{1+1}}=Z_{p_{2+1}}\), stb. azaz a \(Z_n\) vektorok \(p_2-p_1\) periódussal ismétlődnek. Így az \(f_A(n)\) értékek is. □
Mivel a lehetséges \(\max\{A\}\) hosszúságú 0-1 vektorok száma \(2^{\max\{A\}}\), ez egy felső határ a periódus hosszára. Nyitott kérdés, hogy létezik-e (\(\max\{A\}\) függvényében) exponenciális periódushossz. A játék egy kissé módosított változatában sikerült nemrégiben szuperpolinomiális periódushosszakat bizonyítani [4]. A tipikus periódushossz azonban általában lineáris vagy még rövidebb hosszúságú \(\max\{A\}\) függvényében. Pl. belátható, hogy ha \(A=\{a_1,a_2\}\), akkor a periódushossz \(2a_1\), ha \(a_2\) páratlan többszöröse \(a_1\)-nek, és minden más esetben \(a_1+a_2\) [1]. A nyerő pozíciók periódushosszai csak a kételemű \(A\) halmazok esetén ismertek teljes egészében.
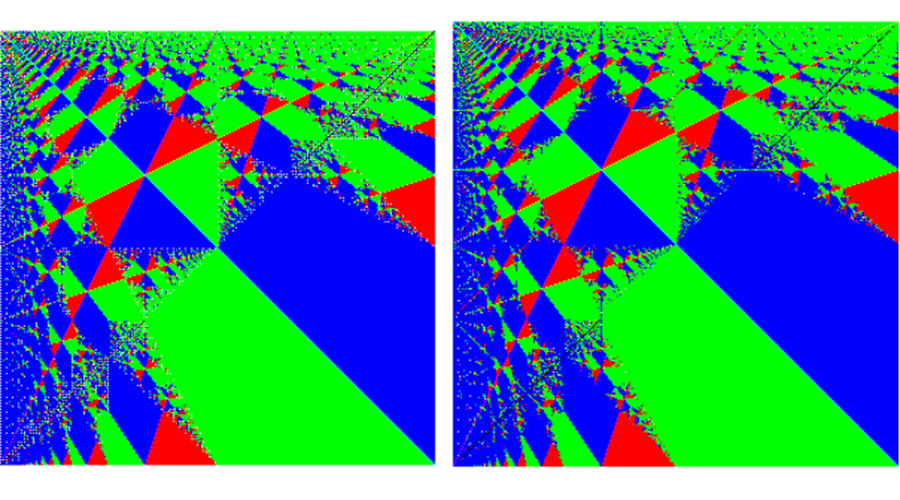
Háromelemű halmazok esetében, pl. ha \(a_1=s\), \(a_2=2s+1\) és \(a_3=3s+1\), akkor a periódushossz \(4s^2+3s\) [1]. Nem ismert négyzetesnél hosszabb periódushossz, és a legtöbb esetben a periódushossz vagy \(a_1+a_2\) vagy \(a_1+a_3\) vagy \(a_2+a_3\), vagy ennek a három számnak az osztója [2]. Itt a következő érdekes jelenséget figyelhetjük meg. Ha egy fix nagy \(a_3\) értékre ábrázoljuk minden lehetséges \(A=\{a_1,a_2,a_3\}\)-ra, hogy az \(f_A\) függvény periódushossza a fenti három összeg közül melyiknek az osztója (esetleg több összegnek vagy egyikének sem), akkor az 1. ábrán látható fraktálstruktúrát kapjuk. Ennek a fraktálnak a struktúrája lényegében nem függ \(a_3\)-tól. Az 1. ábrán \(a_3=293\)-ra és \(a_3=300\)-re mutatjuk, hogy melyek azon \({(a}_1,a_2)\) párok, amelyekre az \(f_A\) függvény periódusa \(a_1+a_2\) osztója vagy \(a_1+a_3\) osztója vagy \(a_2+a_3\) osztója. Míg 293 prím, 300 összetett szám. Ennek ellenére a két esetben kapott ábra nagyon hasonlít egymásra. Egyelőre nem ismert ennek a jelenségnek a magyarázata.

Még érdekesebb jelenségeket figyelhetünk meg, ha a játékot úgy játsszuk, hogy nem 1, hanem 2 kupac kavicsunk van, és az \(A\) halmaz véges, kétdimenziós nemnegatív egész vektorokat tartalmaz (legalább az egyik vektor koordináta pozitív). A két játékos ismét felváltva játszik, és minden lépésben az \(A\) halmazból választanak egy vektort, amely megmondja, hogy melyik kupacból hány kavicsot kell elvenni. Amennyiben a maradék kavicsok száma annyi, hogy egyetlen \(A\)-beli vektor sem választható (mert legalább az egyik kupacban levő kavicsok száma kevesebb, mint a vektor megfelelő koordinátája), az aktuális játékos elveszíti a játékot, és a másik nyert. Ekkor definiálhatjuk az \(f_A(n_1,n_2)\) függvényt a következőképpen. \(f_A(n_1,n_2)=1\), ha \(n_1\) és \(n_2\) kaviccsal kezdve a kezdő játékosnak van nyerő stratégiája, és \(f_A(n_1,n_2)=0\), ha a második játékosnak van nyerő stratégiája. Fennáll a
\[\displaystyle f_A(n_1,n_2)=1-\min\limits_{(x_1,x_2)\in A} \{f_A(n_1-x_1,n_2-x_2)\}\]
egyenlőség, amelynek segítségével könnyen ki tudjuk számolni az \(f_A(n_1,n_2)\) értékeket.
Míg egydimenziós esetben skatulyaelvvel könnyen lehetett bizonyítani a periodikusságot, addig két dimenzióban nem ismert ilyen bizonyítás, sőt, úgy néz ki, hogy bizonyos esetekben az \(f_A(n_1,n_2)\) függvény kaotikus viselkedést mutathat. Kaotikus viselkedést gyakran figyelhetünk meg olyan \(A\) halmazoknál, amelyek tartalmaznak egy olyan \(x_{\max}\) vektort, amelyre minden \(x\in A\), \(x\neq x_{\max}\)-ra \(x_{\max}-x\in A\) [3]. Ezek közül most az \(A=\{(3,0),(0,3),(2,5),(5,2),(5,5)\}\) esetet mutatjuk be. Ekkor az átló körüli, azaz \(n_1\approx n_2\) tartományban teljes káoszt mutat az \(f_A(n_1,n_2)\) függvény (ld. 2. ábra), míg az átló alatt függőleges, az átló fölött vízszintes irányban periodikusságot mutat \(f_A(n_1,n_2)\), de a másik irányban kaotikus viselkedést mutat (ld. 3. ábra). Ide kattintva erre a játékra \(f_A(n_1,n_2)\) első 16000-szer 16000 értékeit mutatjuk be. További két \(A\) halmazra ugyanennyi értéket mutatunk be, itt az \(A=\{(1,9),(8,3),(9,1),(2,7),(10,10)\}\), itt pedig az \(A=\{(2,9),(8,3),(8,1),(2,7),(10,10)\}\) halmazhoz tartozó \(f_A(n_1,n_2)\) függvény értékeit. A \((0,0)\) a bal felső sarokban van. A fekete szín jelöli az \(f_A(n_1,n_2)=1\) értéket, a fehér szín pedig a \(f_A(n_1,n_2)=0\) értéket.


Miklós István
HUN-REN Rényi Intézet
Hivatkozások
[1] I. Althöfer, and J. Bültermann. Superlinear period lengths in some subtraction games. Theoretical Computer Science, 148 (1995) No 1, 111–119, 1995.
[2] U. Larsson, I. Saha, A brief conversation about subtraction games, https://arxiv.org/abs/2405.20054. (2024)
[3] U. Larsson, I. Saha, M. Yokoo, Subtraction games in more than one dimension, https://arxiv.org/abs/2307.12458. (2024)
[4] I. Miklós, L. Post, Superpolynomial period lengths of the winning positions in the subtraction game. International Journal of Game Theory, 53(2024), 1275-1313.