2024. januárjában a középiskolai felvételiken már azok a diákok fognak részt venni, akik az elmúlt 4 évben az új NAT szerint tanultak, az új kerettantervek szerint írt tankönyveket használták. Tanároknak és szülőknek is sok fejtörést okoz, hogy milyen változást hozhat ez a tény a központi felvételi feladatsorokban. Ezzel az írással szeretném áttekinteni az elmúlt évek felvételi feladatsorainak szerkezetét. Én sem tudom, hogy milyen lesz a januári felvételi, de néhány gondolatot leírok majd arról, hogy miben változhatott a diákok tudása, milyen témákra lenne jó még a felvételi előtti hónapban egy kicsit erősíteni. Mindezt sok évi tapasztalat alapján, de nem a feladatsorok készítőjeként írom, akár tévedhetek is.
Ebben az írásban a gondolataimat az alábbi tényekre alapozva írtam:
1. A most felvételiző nyolcadikosok 1-4. osztályokban a 2012-es NAT szerint, az 5-8. osztályokban a 2020-as NAT szerint tanultak. Az ezek alapján készült kerettantervek az Oktatási Hivatal honlapján érhetők el.
2. Szintén a hivatal honlapján találunk tájékoztatást a magyar és matematika írásbeli feladatlapokról. Ebben az anyagban olvasható ez a mondat is:
A feladatlapok összeállításának szempontjai, a feladattípusok belső arányai a korábbi évekhez képest alapvetően nem változnak, így az OH honlapján megtalálható korábbi feladatsorok továbbra is segítik a felkészülést.
3. Az írásbelin ebben a tanévben szereplő témakörökről is tájékoztat az OH honlapja:
4. Simon Judit tanárnő a facebook Matematikatanítás felső tagozaton (5–8 osztály) TANÁRI CSOPORT számára készített egy összehasonlító táblázatot, amelyben összehasonlítja a korábbi évek követelményeit a mostaniakkal.
A változások röviden így foglalhatók össze:
Kikerült a követelményrendszerből:
– a normál alak ismerete;
– egyenletek megoldása, helyette elsőfokú egyenletek megoldása szerepel;
– függvény, értelmezési tartomány, értékkészlet fogalma, meghatározása egyszerű esetekben, függvény megadási módjai, függvény és grafikonja;
– lineáris függvények ábrázolása képlet alapján, táblázattal és paraméterei alapján;
– egybevágóság általános fogalma nem szerepel, de háromszögek egybevágósága igen;
– kerület-, területszámítás általánosan nincs, de szerepel a háromszög, paralelogramma, trapéz és deltoid kerülete, területe;
– a háromszög köré írt körének fogalma, tulajdonságainak alkalmazása feladatmegoldásokban;
– a háromszög beírt körének fogalma, tulajdonságainak alkalmazása feladatmegoldásokban;
– a háromszög magasságvonala, magasságpontja;
– a kör kerülete és területe;
– a henger felszíne és térfogata.
Bekerült a követelményrendszerbe:
– számrendszerek ismerete;
– megfeleltetés, arányos osztás, egyenes arányosság, koordináta-rendszer, pont koordinátái. grafikon.
Hogyan készüljünk? Hogyan gyakoroljuk?
Nem tudunk mást tenni, mint hogy a régebbi évek feladatsorait használjuk. De lesznek olyan feladatok, amelyeket a mostani nyolcadikosok nem tanultak, vagy nem olyan mélyen tanultak. Ezeket a feladatokat kivehetjük a feladatsorból.
Aki a korábbi években felvételire készített elő diákokat, az tudja, hogy jól meghatározott típusfeladatok vannak ezekben a feladatsorokban. Beszélgethetnénk arról, hogy jó-e ez vagy sem. De most ne tegyünk ilyet. Megmondhatjuk, hogy milyen szokott lenni az első, a második, a harmadik feladat… Ezt érdemes átgondolni és tudatosítani magunkban. A diákoknak, a matematikából nem extrán tehetségeseknek különösen fontos, hogy ezeket az ötleteket begyakorolják, rutint és bátorságot szerezzenek a típusfeladatok megoldásában. Az utolsó három feladat már változatosabb, nehezebb. Ezek megoldása ad komolyabb pontszámot, ha a tanítványunk egy erős középiskolába felvételizik.
Az alábbiakban válogattam 10 feladatot az elmúlt 10 évből. Megfogalmaztam azt is, hogy a feladatsor adott sorszámú feladata sokszor milyen ismeretet kér számon. Persze ez nem szabály, amitől ne lehetne eltérni, de elindulásnak, kiindulópontnak használható. Mindegyik feladat más évből való, de akár egy feladatsorban is lehetnének…
1. Számolási műveletek, egész számok, törtszámok, műveleti tulajdonságok
2012. január 21. 1. feladat:
Határozd meg az \(a\), \(b\), \(c\) és \(d\) értékét, és írd a megfelelő helyre!
a) \(a=-5{,}2-(-3{,}4)\)\(a=\)
b) \(b=10{,}2:(-3)\)\(\!b=\)
c) \(c\cdot 0{,}6=6\)\(c=\)
A fenti eredmények ismeretében határozd meg a \(d\) értékét! Írd le a számolás menetét is!
d)–e) \(d=5a+0{,}6c\)\(d=\)
Általában ehhez hasonlóak a feladatsorok első feladatai. Az is jellemző, hogy néhány részfeladat eredményéből egy további számolás során egy betűs kifejezés értékét kell kiszámítani, ahogy ez a feladat is mutatja.
2. Mértékegység-átváltások
2013. január 19. 2. feladat:
Tedd igazzá az alábbi egyenlőségeket a hiányzó adatok beírásával!
a) \(16{,}5~{\rm hl} + 32~{\rm l}=\;\) \(~{\rm l}\)
b) \(2013~{\rm s} = 30~{\rm min}+\;\) \(~{\rm s}\)
c)–d) \(36{,}28~{\rm t}=\;\) \(~{\rm kg} =\;\) \(~{\rm kg} − 40~{\rm kg}\)
Sokszor szerepel a mennyiségek összeadása, kivonása. Gyakoroljunk hasonlókat.
A kerettanterv szerint ezek az elvárások a felső tagozaton:
– ismeri az idő, a tömeg, a hosszúság, a terület, a térfogat és az űrtartalom szabványmértékegységeit, használja azokat mérések és számítások esetén;
– idő, tömeg, hosszúság, terület, térfogat és űrtartalom mértékegységeket átvált helyi értékes gondolkodás alapján, gyakorlati célszerűség szerint.
3. Kombinatorika – adott tulajdonsággal rendelkező konstrukció előállítása
Fel kell sorolni vagy le kell rajzolni bizonyos feltételeknek eleget tevő eseteket.
2014. január 19. 3. feladat:
Luca (L), Krisztina (K), Angéla (A) és Nóra (N) 400 méteres futásban mérték össze az erejüket. A verseny után a következőket mondták el a barátjuknak, Rékának (aki nem látta a versenyt): Sem Luca, sem Angéla nem lett utolsó, sem Krisztina, sem Nóra nem lett első. Milyen sorrendben érkezhettek a célba, ha nem volt holtverseny?
Írd a táblázat mezőibe a versenyzők nevének kezdőbetűit a feltételnek megfelelő valamennyi lehetséges sorrend szerint! Egy lehetséges sorrendet előre beírtunk a megoldások táblázatába.
Megoldásaidat a vastag vonallal körülvett mező táblázataiba kell beleírnod, mivel csak ezeket értékeljük. A többi táblázatban próbálkozhatsz, de azokat NEM értékeljük!
Lehet, hogy a bekeretezett részben több táblázat van, mint ahány megoldás lehetséges.
Vigyázz! Ha a megoldásaid között hibásan kitöltött táblázat is szerepel, azért pontlevonás jár.

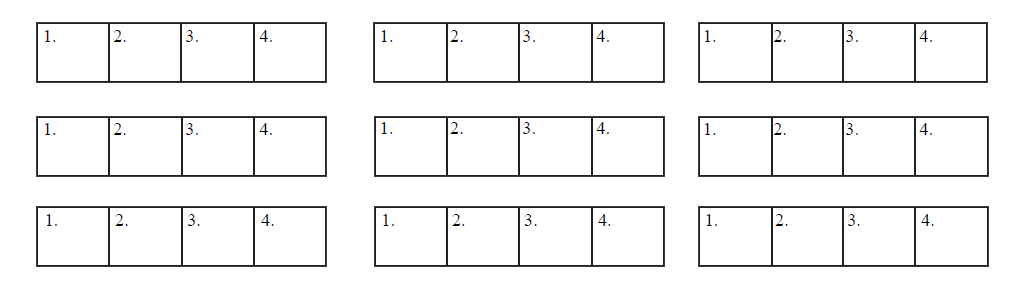
Érdemes felhívni a figyelmet arra, hogy legyen valamilyen stratégiánk az esetek összegyűjtésére. Így kisebb a veszélye annak, hogy valami kimarad vagy többször szerepel.
4. Táblázatból, grafikonról olvasd le! Töltsd ki a táblázatot! Készíts grafikont!
2015. január 17. 4. feladat:
Három különböző korosztályból összesen 400 embert kérdeztek meg, hogy a labdarúgás, vízilabda és kézilabda sportágak közül melyiket szeretik legjobban. Mindannyian válaszoltak.
A felmérés néhány eredménye az alábbi táblázatban található.
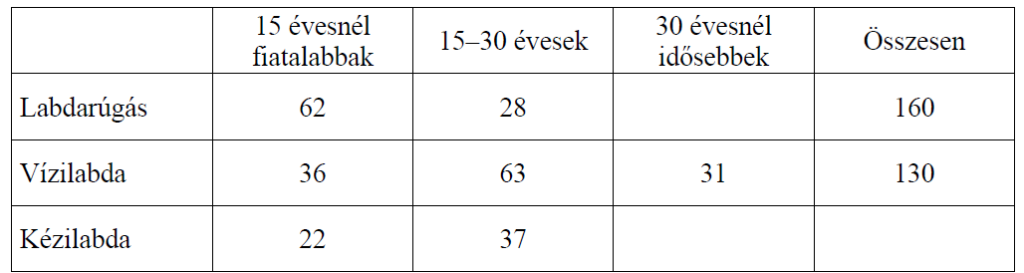
a) Töltsd ki a táblázat hiányzó mezőit!
b)–c) A 15 évesnél fiatalabb megkérdezettek hány százaléka válaszolta azt, hogy a vízilabdát szereti legjobban? Írd le a számolás menetét!
d) Karikázd be annak a kördiagramnak a betűjelét, amelyen a 15 évesnél fiatalabb megkérdezettek válaszainak az eloszlását ábrázoltuk!
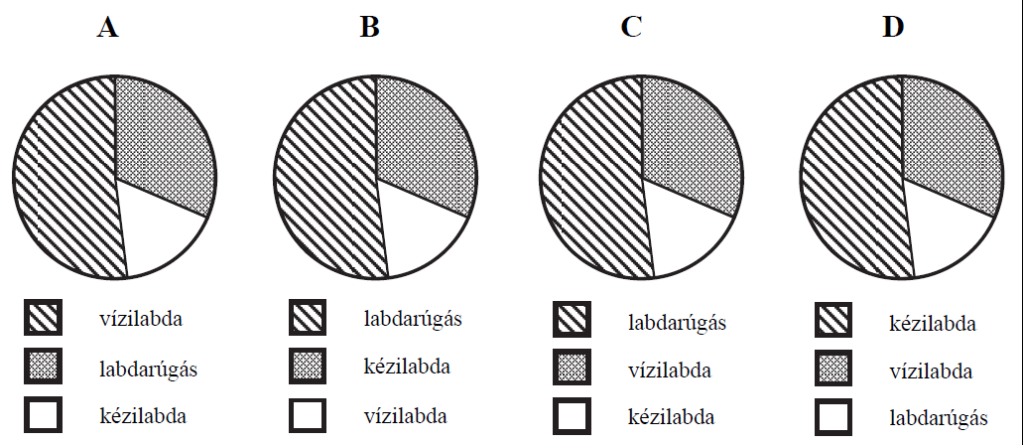
Most olyan feladatot választottam, ahol kördiagram szerepel. Gyakoriak a vonaldiagramok, oszlopdiagramok is. Érdemes azt megbeszélni, hogy milyen tengelyeket használunk, hogyan választunk egységeket, milyen feliratok szükségesek a tengelyekre.
5. Szögek kiszámítása: egyenlő szárú háromszögek, négyszögek tulajdonságai
2016. január 16. 5. feladat:
Az alábbi ábrán az \(e\) félegyenes az \(ABC\) háromszög \(C\) csúcsánál lévő belső szögszögfelezője, az \(f\) egyenes az \(AC\) oldal oldalfelező merőlegese. Az \(e\) és \(f\) metszéspontját \(P\) jelöli. Az \(e\) szögfelező félegyenes az \(AB\) oldalt a \(Q\) pontban metszi. Az ábrán néhány szög nagyságát megadtuk.
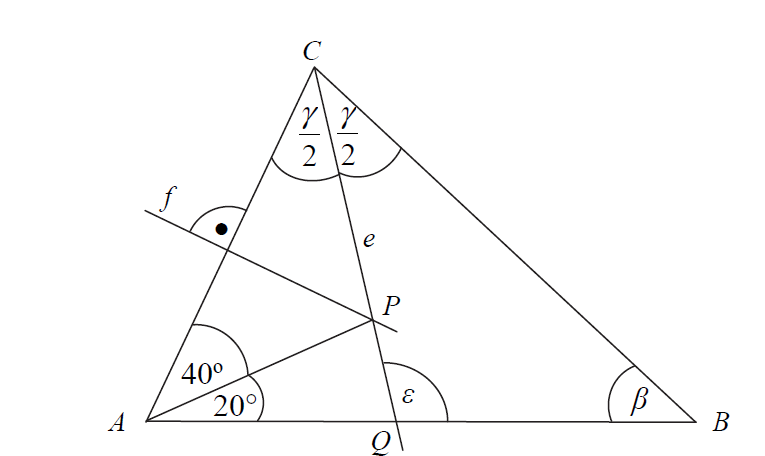
(Az ábra csak tájékoztató jellegű vázlat, nem pontos méretű.)
a) Mekkora a \(\frac{\gamma}{2}\) szög nagysága?
b) Mekkora az \(\varepsilon\) szög nagysága?
c) Mekkora a \(\beta\) szög nagysága?
Az ilyen típusú feladatokban az alapgondolatok ezek lehetnek:
– A szakaszfelező merőleges pontjai egyenlő távol vannak a szakasz végpontjaitól
– Egyenlőszárú háromszög alapon fekvő szögei egyenlőek.
– A háromszög egymás mellett lévő belső és külső szöge \(\color{blue}180^\circ\)-ra egészíti ki egymást.
– A magasságvonal merőleges az oldalra.
– A háromszög szögeinek összege \(\color{blue}180^\circ\), a négyszög szögeinek összege \(\color{blue}360^\circ\).
– Esetleg az ábra tengelyesen szimmetrikus.
6. Egyszerűbb szöveges feladat a feladatsor közepén
2020. január 18. 6. feladat:
Viola macskájának kedvenc cicakonzerve két webáruházból rendelhető.
Az ALFA webáruházban egy ilyen cicakonzerv ára 400 Ft, a kiszállítás egyszeri ára a megrendelt darabszámtól függetlenül 1200 Ft.
A BÉTA webáruházban egy ilyen cicakonzerv ára 425 Ft, de a megrendelt darabszámtól független kiszállítás egyszeri díja itt csak 850 Ft.
Hány cicakonzerv megrendelése esetén kerül Violának ugyanannyiba a vásárlás, függetlenül attól, hogy melyik webáruházból rendel?
Írd le a számolás menetét is!
Ezekben a feladatokban talán ez a kerettantervi elvárás fogalmazódik meg:
Egyszerű szöveges feladat matematikai tartalmának felismerése, és az annak megfelelő műveletsor felírása.
7. Válaszd ki az igaz állítást – Sokszor vegyes témakörökből 3-4 kérdésre vár választ a feladat.
2021. január 23. 7. feladat:
Írj \(\times\)-et a táblázat megfelelő mezőibe!
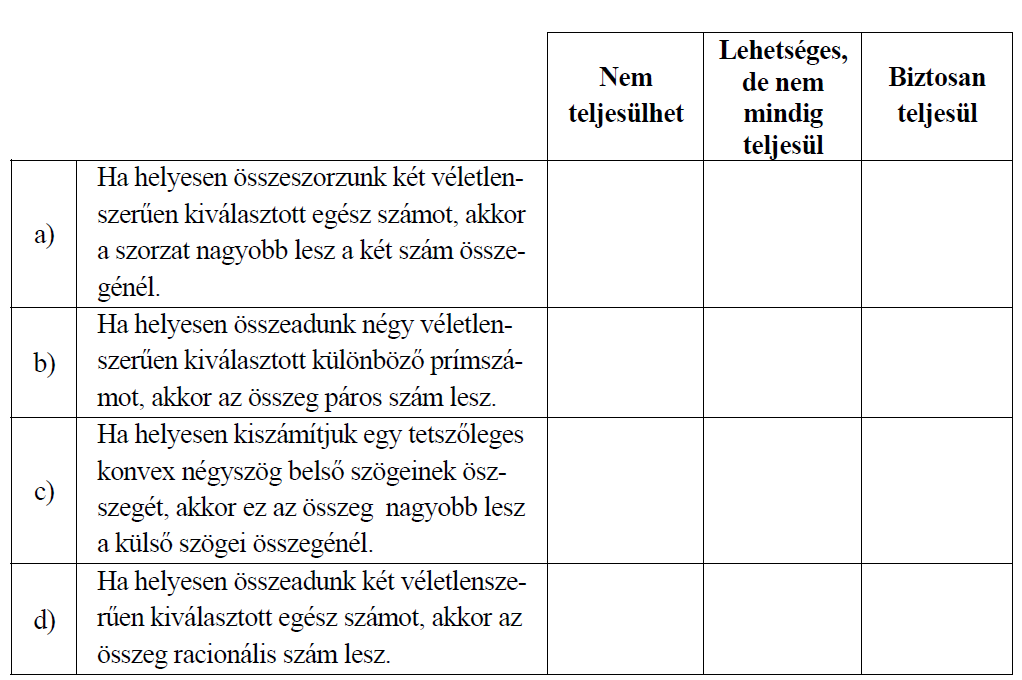
8. Koordináta-rendszer használata
2023. január 21. 8. feladat:
Az \(ABCD\) téglalap csúcsai betűzésének sorrendje \(A\), \(B\), \(C\) és \(D\).
Az \(ABCD\) téglalap szimmetrikus az \(x\) tengelyre úgy, hogy az \(A\) csúcs tükörképe a \(B\) csúcs, a \(C\) csúcs tükörképe a \(D\) csúcs.
Az \(ABCD\) téglalap \(A\) csúcsának koordinátái \((3;2)\).(3; 2).
Az \(ABCD\) téglalap területe 20 területegység.
a) Melyek a \(B\) csúcs koordinátái? \(B(\) \(;\) \()\)
b) Keresd meg mindkét ilyen tulajdonságú téglalapot, és rajzold be az alábbi koordinátarendszerekbe!
A rácsnégyzetek egységnyi oldalhosszúságúak.
Egy koordináta-rendszerbe egy téglalapot rajzolj!
Határozd meg az egyes téglalapok \(C\) és \(D\) csúcsának koordinátáit!
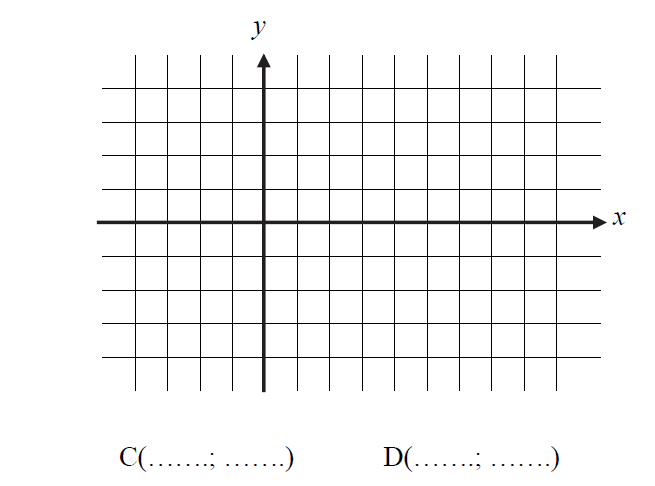
A diákok (persze nem a legokosabbak) gyakran cserélik fel az első és második koordinátát. A fontolva haladókkal ezt érdemes gyakorolni.
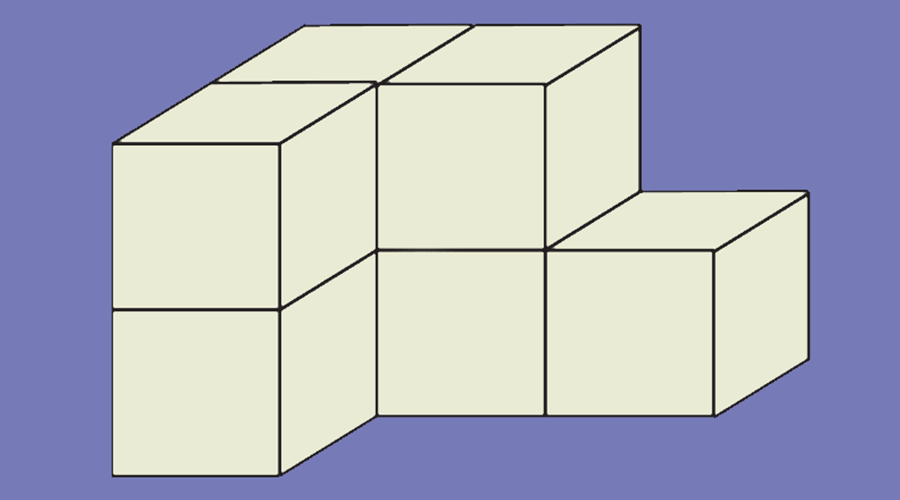
9. Térgeometria – Gyakran néhány kockából, téglatestből álló alakzat ábrája látható a feladatban. Erről kell megállapítani, hogy pl. hány kockából áll, Milyen méretűek a szakaszok, mennyi a felszín, a térfogat…
2017. január 21. 9. feladat:
Hét darab egybevágó kockából ragasztottuk össze az ábrán látható testet. Két szomszédos kocka egy-egy teljes lapjával van összeragasztva. Egy kocka térfogata \(8~\text{cm}^3\).
(Az ábra csak tájékoztató jellegű vázlat, nem pontos méretű.)
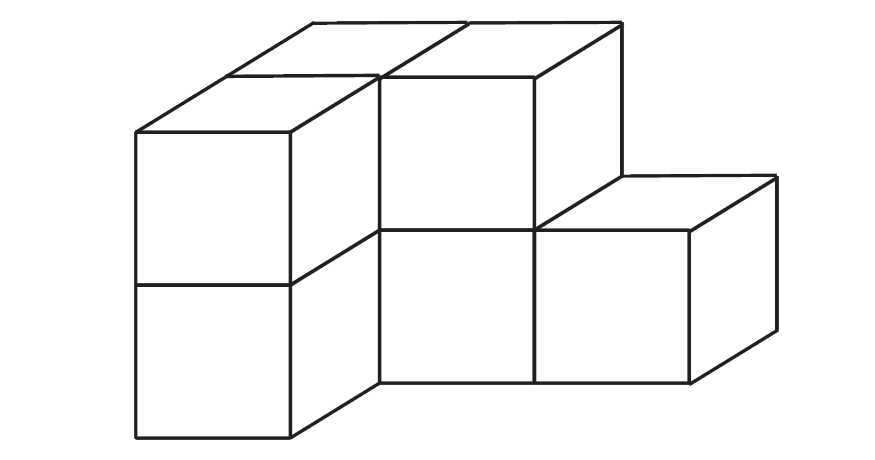
a) Hány cm hosszú egy kocka éle?
b) Hány cm az ábrán látható test leghosszabb éle?
c) Hány \(\text{cm}^2\) az ábrán látható test felszíne?
Írd le a számolás menetét is!
Egy síkbeli ábra alapján nehéz elképzelni a térbeli viszonyokat. Amikor ilyen feladatokat gyakorlunk, rakjuk ki a valóságban is a testeket. Térbeli feladatokhoz, vagy csak egy kis játékhoz is használjunk építőkészleteket.
10. Nehezebb szöveges feladat
2022. január 22. 10. feladat:
A városi labdarúgóklub toborzót rendezett, amelyre előzetesen kellett jelentkezni. Az előzetesen jelentkezők \(\frac{1}{15}\) része nem jelent meg a toborzón. A megjelentek \(\frac{5}{7}\) része teljesítette a fizikai felmérés követelményeit, a többiektől elbúcsúztak az edzők.
A fizikai felmérést eredményesen teljesítőknek labdás gyakorlatokat kellett végezniük, amelyeket 40%-uk teljesített hibátlanul, őket leigazolta a klub.
A városi labdarúgóklubnak 28 új igazolt játékosa lett.
Hányan jelentkeztek előzetesen a toborzóra?
Írd le a számolás menetét is!
Az „utolsó szöveges feladatra” nem csak a tankönyvi feladatok megoldásával készülhetünk. Válogassunk a versenyfeladatokból, az ABACUS újság feladataiból is.
Felsorolok néhány további témakört, amely az elmúlt 5 év feladatsoraiban szerepelt:
– adott mennyiség tört része, százalékszámítás;
– arányok, arányos osztás;
– számok kerekítése;
– oszthatóság, osztók száma;
– betűs kifejezés helyettesítési értéke.
Természetesen a felvételi anyaga nem ennyire leszűkített típusfeladatokban mutatható be. Minden bizonnyal az iskolákban a 8 év alatt ennél tágabb témakörökkel foglalkoztak, a diákok matematikai gondolkodása sokféle módon fejlődött. Sokan még meg is szerethették a matematikát. A célegyenesben se csak felvételi feladtasorokat oldjunk meg – „minél többet” jelszóval. Válogassunk érdekes, gondolkodtató feladatokat is más feladatanyagból, gyűjteményből. Ezen nem feltétlenül nehezeket értek. A sikerélménnyel a diákjaink bátorságát, önbizalmát is növelhetjük.
Az új NAT-tal kapcsolatban végezetül két témakört emelek ki, amire érdemes figyelnünk mind a tanítás során, mind a felvételire készülve:
– A korábbi években a függvények tanítása is szerepelt az általános iskola felső tagozatában: elsőfokú, másodfokú, abszolútérték. egészrész … stb. Egyszerű függvénytranszformációk is előfordultak.
Most a függvények teljesen kimaradnak. Az ehhez kapcsolható fogalmak viszont nem egészen, „megfeleltetés” címmel szerepelnek „A függvény fogalmának előkészítése” témakörben. A kerettanterv így fogalmaz: Konkrét megfeleltetések legalább egy lehetséges szabályának megadása. Nincs elsőfokú függvény, de van egyenes arányosság és annak grafikonja. Vannak fordítottan arányos mennyiségek. És táblázatokba összetartozó értékeket írunk be, grafikonokat rajzolunk és elemzünk.
– A betűs kifejezések használatával a gyerekek egyszerű formában már a 6. évfolyamon találkoztak. Az új NAT szerint ez a 7. évfolyamra került. Ebből következik, hogy az egyenletek felírásában, megoldásában is kisebb rutinra tehettek szert a diákok. Felvételi előtt, a nehezebb szöveges feladatokat gyakorolva erre is gondoljunk.
Végezetül a felkészítő tanároknak, szülőknek és nem utolsó sorban a diákoknak is kitartást és derűt is kívánok a januári írásbelire való készüléshez.
Horváth Eszter, a Tanóra–szakkör rovat szerkesztője
Irodalomjegyzék
1. https://www.oktatas.hu/kozneveles/kerettantervek
2. https://www.oktatas.hu/kozneveles/kozepfoku_felveteli_eljaras/tajekoztato_matek_magyar
4. https://www.facebook.com/groups/355332874634288/permalink/2546344378866449