0. Bevezető
Ez a rövid cikk alapvetően didaktikai szándékú és fő célja, hogy megmutassa a XX. század egyik legkiemelkedőbb magyar matematikusának, Neumann Jánosnak egy igazán világraszóló eredményét, pontosabban az ahhoz vezető fő gondolatokat, amit ma „Minimax-tételnek” vagy a játékelmélet alaptételének is neveznek. A leírtak alapján akár egy középiskolai kísérleti kipróbálást is meg lehet szervezni, amit a szerző meg is tett évekkel ezelőtt több vidéki és fővárosi iskolában.
Két, nem csak a matematikus világban világhírűvé vált János született majdnem pontosan 100 év különbséggel a XIX. és a XX. században. Mindketten a világon valaha élt legjelentősebb matematikusok közé tartoznak. Ezért is fontos lenne az iskolában mindkettőjükről beszélni, hiszen magyar tanuló számára a matematika szó elhangzásakor legalább ezek a nevek be kellene, hogy ugorjanak. Egyikük Bolyai János (1802-1860), akinek a nem-euklideszi geometriát köszönhetjük, s amelynek iskolai bemutatása először Lénárt István1 gömbjeivel vált lehetővé. Bolyai elismerése tragikus élete során nem, csak halála után kezdődött, igaz azóta is töretlen.
Eredménye a modern matematika egyik előfutárává tette, aki évtizedekkel megelőzte korát. Ennek az úttörő szerepnek a bemutatására egy tudományelméleti megközelítést választó beszélgetésre utalnék, amely Staar Gyula könyvében [1] olvasható a Tóth Imrével folytatott dialógusban. Munkásságának igazi jelentősége remekül kiviláglik Tóth matematika filozófiai fejtegetéséből. Az olvasónak ajánljuk a beszélgetés megismerését.


Másikuk a már említett Neumann János (1903-1957), aki a számítógép működési elvének és mechanizmusának kidolgozása és megvalósítása (az ENIAC első számítógép) mellett nagyon sok alapvető eredményt ért el a matematikában és az elméleti fizikában. Hozzá fűződik a Schrödinger-féle hullám-mechanika és a Heisenberg-féle mátrix-mechanika izomorfiájának igazolása.
Ez egy nagyon mély eredmény, ma is csak a felsőoktatásban szerepelhet, ahol évtizedek óta egy másik nagy teljesítménye a játékelmélet is szerepel, lásd [3]. Ezúttal az utóbbiról szeretnénk azt megmutatni, hogy hamarabb is előkerülhetne, már akár középiskolában is, bár természetesen csak egy egyszerű esetben. Ehhez első lépés egy ilyen játék ismertetése, amit a következő fejezetben meg is teszünk.
1. Egy egyszerű játék a snóbli2 alapján
Két játékos játszik úgy, hogy mindkettőnek két lehetősége van, vagy tesz egy pénzérmét a kezébe vagy nem. Majd mindketten előrenyújtják az összezárt kezüket és egyszerre kinyitják. Az első, nevezzük őt \(A\) játékosnak, nyer, ha a két kéz szimmetrikus, azaz mindkettő üres vagy mindkettőben van egy-egy érem. A másik, \(B\) nyer, ha aszimmetrikus, azaz ha az egyikben van pénzérme, míg a másikban nincs. Abban is hasonlít a játék a snóblira, hogy a nyeremény a kezekben levő pénzérmék összege. De mivel, ha senki nem tett, akkor 0 lenne a nyeremény, ezért a pénzérmékhez a vesztes még egyet hozzátesz. Így az alábbi, ún. kifizetési mátrixszal írhatjuk le a játékot:
| \(\downarrow\ A\) játékos; \(B\) játékos téte \(\rightarrow\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(-2\) |
| \(1\) | \(-2\) | \(3\) |
A kérdések a következők:
- ) Milyen stratégiát kövessenek a játékosok?
- ) Igazságos-e a játék vagy valakinek kedvez?
A kérdések megválaszolását megelőzheti a játék kipróbálása, amelynek tapasztalatait a következőkben összegezzük.
2. A játék elemzése stratégiai szempontból
Mindkét játékos számára fontos, hogy kiismerhetetlen legyen a játéka, mivel ellenkező esetben veszteni fog, bármelyik szerepben is van. Pl. ha A tudja mit fog lépni B, akkor ugyanazt teszi ő is, hiszen szimmetrikus esetben ő nyer. Ugyanez igaz B-re is, csak ő ekkor éppen ellenkezőképpen fog cselekedni, s nyer. Azaz mindkettőjük számára fontos a kiismerhetetlenség. De hogyan is lehet a viselkedésem kiismerhetetlen? Ha véletlenszerű, hiszen ekkor nem tudja a másik, mi fog történni. Bármilyen rafinált determinisztikus stratégiával is játszom, egy idő múlva felismeri a másik, s meg tudja jósolni a következő lépésemet. A nem tét és a tét egy \(0\), \(1\) sorozattal írható le. Ha akár A, akár B felismer valami szabályszerűséget partnere \(0\), \(1\) sorozatában, akkor onnantól kezdve nyerni fog. Ezzel azonban még csak az első lépést tettük meg Neumann János gondolatmenetében. Itt jegyezzük meg azt, hogy a véletlennek egy lehetséges meghatározása éppen a bonyolultság segítségével lehetséges. Ha egy \(0\), \(1\) sorozatot nem lehet lényegesen rövidebb hosszúságú programmal leírni, mint a sorozat elemeinek száma, akkor mondjuk véletlennek sorozatnak. Ezzel ma egy új matematikai elmélet a bonyolultságelmélet foglalkozik, melyet nem meglepően éppen az a matematikus kezdeményezett Chatain amerikai kollégájával, aki a valószínűségszámítás matematikai megalapozását is elvégezte, azaz A. N. Kolmorogov3. Egy Lovásztól származó egyetemi jegyzet 6. fejezetében olvashatunk erről bővebben, lásd [4] 109. oldaltól.
A következő kérdés persze az, hogy milyen véletlen generátorral játsszak. Más szavakkal, mi legyen a „teszek a kezembe pénzt” vagy a „nem teszek” valószínűsége? Vajon léteznek-e olyan valószínűségértékek, amelyek „optimálisak” abban az értelemben, hogy a tőlük való eltérés hátrányos a játékos(ok)nak. Elemezzük a helyzetet. Ha a két játékos egymástól függetlenül \(p\) és \(q\) valószínűséggel tesz pénzérmét a kezébe, akkor az \(A\) játékos nyereményének várható értéke a két egyelőre ismeretlen valószínűséggel a következőképpen írható fel:
(1)\(\displaystyle N(p,q)=3pq-2p(1-q)-2p(1-p)+(1-p)(1-q).\)
Két dolgot használtunk fel, a várható (nyeremény)érték fogalmát, valamint az események függetlensége esetén fennálló szorzási szabályt. Tehát, hogy például \(A\) tesz és \(B\) nem tesz, annak esélye éppen \(p(1-q)\). Vizsgáljuk most meg ezt a kifejezést.
Egyúttal vegyük észre, hogy \(B\) várható nyereménye éppen \(-N_A(p,q)\), azaz amikor \(B\) nyereménye maximális, akkor \(A\) nyereménye minimális és fordítva, mivel pénzt csak egymástól nyernek el. Ha nincs se külső pénzforrás, se pénznyelő, akkor az ilyen játékokat szokás zérusösszegű játéknak nevezni, mivel a játékosok „nyereményeinek” összege mindig \(0\). Mielőtt tovább vizsgálnánk a helyzetet, alakítsuk át (1)-et, a beszorzások elvégzésével és az egynemű tagok összevonásával adódik
(2)\(\displaystyle N_A(p,q)=8pq-3p-3q+1\).
Iskolás feladat, hogy egy kifejezést alakítsunk szorzattá, lehetőleg úgy, hogy az egyik tényezőben csak a p, a másikban csak a q szerepeljen. Így kapjuk
(3)\(\displaystyle N_A(p,q)=8\left(p-\dfrac{3}{8}\right)\left(q-\dfrac{3}{8}\right)-\dfrac{1}{8}\).
Most kezdhetjük bemutatni Neumann János gondolatát, amelyben feltételezi, hogy mindkét játékos intelligens, s a számára legjobb megoldást képes választani. A feltételezi, hogy \(B\) nagyon okos, tehát olyan \(q\) értéket választ, ami mellett nyeresége maximális, azaz \(A\) nyereménye minimális. Ezután jön a saját „okossága”, ami olyan \(p\) választást jelent, hogy a nyereménye maximális legyen. Ezt úgy fejezhetjük ki, hogy keressük a következő kettős szélsőértéket: \(\max_p\min_q N_A(p,q)\). Ugyanez \(B\) szemszögéből \(\min_q\max_p N_A(p,q)\). Akkor van optimális megoldás mindkét játékosnak, ha a két szélsőértékhely egybeesik. Neumann éppen azt bizonyította, hogy két játékos zérusösszegű játéka esetén mindig vannak olyan valószínűségek a döntési lehetőségeik halmazán, amely mindkettőjüknek a lehető legjobb. Ha ilyenkor a nyeremény várható értéke \(0\), akkor igazságosnak mondjuk a játékot. Az optimumot az egységnégyzeten ábrázolt felületet szemlélve, amit az \(N_A(p,q)\) függvény grafikonja rajzol ki, érthető, miért hívjuk nyeregpontnak. Lásd a mellékelt két ábrát illusztrációként.
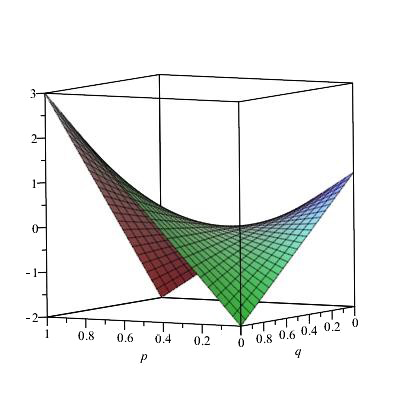
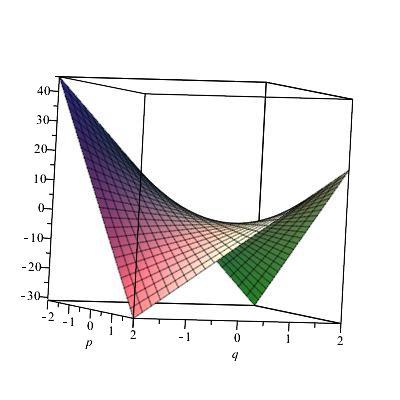
Neumann számára az ötletet, amelyből kiindulhatott, a Young-tétel adhatta, mely szerint a kétváltozós függvény változók szerinti parciális deriváltjainak esetében a deriválás sorrendje felcserélhető, formálisan: \(\frac{\partial^2N(p,q)}{\partial p\partial q}=\frac{\partial^2N(p,q)}{\delta p\delta q}\). Egyébként ezt a (2)-beli kifejezésünkön elvégezve is láthatjuk. Ha először \(p\) szerint deriválunk, a másik változót paraméternek véve, akkor kapjuk: \(\frac{\partial N(p,q)}{\partial p}=8p-3\). Ezt tovább deriválva, most \(q\) szerint, adódik \(8\). Ha fordított sorrendben végezzük el a parciális deriválást, akkor első lépésben \(8p-3\) adódik, s ezt most \(p\) szerint deriválva, szintén \(8\) lesz az eredmény. A tételnek természetesen feltételei vannak, amelyek esetünkben teljesülnek. Ennek általában egy \(n\) változós analógiája szükséges, lásd a 3. paragrafusát ennek a cikknek. Ezen túl azt is igazolni kell, hogy a szélsőérték az egységnégyzet (egység-hiperkockába) belsejébe vagy legfeljebb a határára esik, mivel itt valószínűségek szerepelnek, melyek \(0\) és \(1\) közé kell, hogy essenek. Erre még visszatérünk.
Először vizsgáljuk meg a (3) kifejezést. Itt világos, hogy mivel a két paraméter különböző tényezőkben szerepel, látszik, hogy a másik játékától egy módon függetleníthetem magam, ha a saját tényezőmet \(0\)-vá teszem, mert akkor a szorzat a másiktól függetlenül \(0\) lesz. Azaz mindkettőnek ez célszerű választás (esetünkben \(p = 3/8\) és \(q = 3/8\)), hiszen ilyenkor nem is kell a másikat figyelni. Azonban az is látható, hogy bármelyiküknek veszteséges lehet az ettől való eltérés, ha a másik elég intelligens. Akár \(A\), akár \(B\) szempontjából elvégezhetjük az eltérést a fentebb meghatározott \(p\) és \(q\) értéktől akár felfelé, akár lefelé. Egy esetet bemutatunk, a másik hármat az olvasó is elvégezheti. Tehát pl. \(A\) játékos felfelé eltér a \(p = 3/8\) értéktől. Ezt, ha sokszor játszanak a megfelelő relatív gyakoriságból észreveszi \(B\). Mivel neki a függvény minél kisebb értéke a célja (ha \(A\) nyeresége minimális, akkor az övé maximális) ezért ő lefelé fog eltérni a \(q = 3/8\) értéktől. Ekkor mivel a szorzat negatív lesz (ezért tér el éppen ellentétes irányban, mint \(A\)) több, mint \(1/8\) lesz a nyeresége átlagosan partinként. Tehát ha \(A\) intelligens, akkor jobb, ha nem tér el felfelé a \(3/8\)-tól. ugyanez igaz a lefelé eltérésre is. Ezért nevezzük ezt optimális értéknek számára. Hasonló érveléssel mondható el ez \(B\)-ről is. Azaz mindenféle mélyebb analízis ismeret nélkül, pusztán elemi algebrai okoskodással ebben az esetben megmutatható, hogy van mindkettő számára optimális valószínűség és ezzel játszva, a játék partinként átlagosan \(1/8\) egységet hoz \(B\)-nek. Tehát a játék nem igazságos. Ha választhatunk, akkor \(B\) szerepét kell kérnünk. Jó gyakorlás annak meggondolása, hogy a mi kifizetési mátrixunkban egyetlen szám megváltoztatásával, hogyan lehetne elérni az igazságosságot.
Megjegyeznénk azonban egy „hamis okoskodást”, amellyel amellett lehetne érvelni, hogy ez volt az igazságos. \(B\) mindenképpen \(2\) egységet nyer, ha nyer. \(A\) átlagosan szintén \(2\) egységet, mivel \(1\) és \(3\) átlaga is \(2\). Ezért sokan igazságosnak gondolják a játékot. A hiba ebben a gondolatban az, hogy nem a \(p = \frac12\) az optimális stratégia, ezért \(A\) nem az átlagot nyeri partinként átlagosan!
3. Az egyszerű \(\mathbf{2\times 2}\)-es játék általánosítása és az alaptétel kimondása
A bemutatott és elemzett játék egyszerű általánosítása, ha nem csak két lehetőség van a játékosok számára, hanem több, pl. mindegyik tehet \(1\) vagy \(2\) vagy \(3\) érmét is. Ekkor mindkettőnek \(4\) lehetősége van. Ehhez is kell egy kifizetési mátrixot rendelni, s akkor megkérdezhető, hogy ezúttal miként játszanak. Egy példát adjunk erre a következő mátrix segítségével, folytatva a szimmetrikus \(A\) és az aszimmetrikus \(B\) játékos elvét és a pénzérmék összege plusz egy elvet a nyeremény meghatározásához. Ezt követve kaphatjuk meg a következő kifizetési mátrixot vagy inkább táblázatot:
| \(\downarrow\ A\) játékos; B játékos téte \(\rightarrow\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(0\) | \(1\) | \(-2\) | \(-3\) | \(-4\) |
| \(1\) | \(-2\) | \(3\) | \(-4\) | \(-5\) |
| \(2\) | \(-3\) | \(-4\) | \(5\) | \(-6\) |
| \(3\) | \(-4\) | \(-5\) | \(-6\) | \(7\) |
A nyeremény várható értékét kell itt is felírni, ahol az \(A\) játékos négy lehetséges választásának esélyei legyenek \(p_0\), \(p_1\), \(p_2\), \(p_3\), míg hasonlóan a \(B\) játékoséi: \(q_0\), \(q_1\), \(q_2\), \(q_3\). Ezekkel a jelölésekkel kapjuk:
(4) \(\displaystyle N_A(p,q)=\sum\limits_{i=j}(i+j+1)p_iq_j-\sum\limits_{i\neq j}(i+j+1)p_iq_j\)
továbbá \[\displaystyle\sum\limits^3_{i=0}p_i=\sum\limits^3_{j=0}q_j=1.\]
Azonban most lesz egy nagy nehézség az eddig bemutatott módszerrel kapcsolatban, nevezetesen most már legalább három \(p\) és \(q\) érték kell, azaz \(6\) ismeretlenes lesz a várható nyeremény-függvény, egyet a két feltétel miatt kifejezhetünk a többivel. Ennek szemléltetésére egy hétdimenziós térre lenne szükségünk. Így a „nyeregpont” már nem látszik, ezért a szemléletes megoldás kiesik, másrészt a fentebb leírt szorzattá bontás esetleg akár több tényezővel, de úgy, hogy ezek közül egyesek csak p-ket, mások pedig csak \(q\)-kat tartalmaznak, nem vezet eredményre. Már a kisebb háromszor kettes esetben is baj van, tehát ha csak az egyiknek van \(3\) lehetősége. Ezekben az esetekben már komolyabb eszközökre van szükség, amelyet ma éppen pl. a számítógépek segítségével lehet elvégezni. Az alaptétel szerint ilyenkor is van optimális valószínűség-eloszlás a lehetőségeink halmazán, amelytől sem \(A\), sem \(B\) nem tér el, ha intelligens játékosok. Neumann tétele tehát az egzisztenciáról szól, ezt sikerült belátnia még 1928-ban megjelent cikkében [5]. A tétel a következő:
Ha van egy kétszemélyes zérusösszegű játék, akkor mindig létezik mindkét játékos számára olyan optimális kevert4 stratégia, amelytől való eltérés nem kedvező, azaz mindig létezik nyeregpontja a játéknak. Ez az ún. Minimax (Maximin)-tétel, vagy a játékelmélet alaptétele.
Az eloszlás numerikus kiszámítása azonban bonyolult feladat. Az egzisztenciát eredetileg topologikus módszerekkel sikerült Neumannnak igazolnia, mára azonban egészen más módszerek is léteznek, amelyek közül egy már a Morgensternnel írt közös könyvben [3] is megjelenik. A téma történetét elég részletesen ismerteti Kóczy Á. László cikke [6], amelyben beszámol a máig nyúló fejlődéséről is. Csupán az érdekesség kedvéért jegyezzük meg, hogy végül a téma első Nobel- díjasa az a John F. Nash5 lett, aki a nemkooperatív játékok egyensúlyi állapotainak vizsgálata során végzett úttörő munkásságáért, főleg annak jelentős közgazdasági alkalmazásai miatt megosztva közgazdasági Nobel díjat kapott a magyar származású, Harsányi Jánossal, valamint R. Seltennel 1994-ben. Ez a terület a Neumann-féle elmélet egyik általánosítása.

Milyen meglepő, hogy Harsányi János is éppen a legendás evangélikus Fasori Gimnáziumban tanult és érettségizett, mint Neumann, csak majdnem 20 évvel később. Mindkettejüket ma egy emléktábla örökíti meg az iskolában, a hasonlóképpen itt tanult Wigner Jenővel együtt. A szintén János keresztnév viszont már talán igazi véletlen…
4. Didaktikai megjegyzés
Sokféle oktatási struktúrába illeszthetjük a bemutatott játékot. Lehet akkor foglalkozni vele, amikor már valószínűségszámítást tanultak a diákok (legalább a függetlenség esetén a szorzási szabályt és a várható érték fogalmát is bevezettük már). Ekkor ezekre lehet hivatkozni. Ebben az esetben egy modellezési feladatról van szó, amelyhez a szükséges matematika ismert, tehát alkalmazásról beszélhetünk. Van azonban másik lehetőség is, éppen a valószínűségszámítás tanulásának motiválása, amikor pl. az eloszlások és ezek várható értékének bevezetését szeretnék megcélozni. Ekkor a bemutatott feladat már probléma és éppen az a célja a foglalkozásnak, hogy a megoldáshoz milyen „elméletet” kell, hogy fejlesszünk. Ez az út sokkal időigényesebb, de a megértést és a motiváció által a tanulást is segítheti. Bármely lehetőséget is választjuk, célszerű a játékot sokszor eljátszatni, amit időtakarékosságból lehet szabadidős tevékenység terhére és nem a matematika óra idején folytatni. Ott már csak a megfigyelések összegzése történne. A szerző saját tapasztalatai szerint a véletlen stratégia szükségességére rájönnek a tanulók, azonban a következő lépésben segíteni kell, mármint, hogy mit jelent itt a véletlen szerepe és hogyan lehet „alkalmas” véletlent választani. Azaz a várható érték felírása átlagos tanulóknál (ahol a kísérlet folytatódott) segítség nélkül nem várható el. A megoldás ismeretében a kérdés, hogy milyen esetben lenne igazságos, már nem nehéz, ha csak a főátlóban változtathatunk és az 1-est nem így csak a \(3\)-at lehet módosítani. Mivel jelenleg \(B\)-nek kedvez a játék, \(A\) többet kell, hogy nyerjen, így \(3\)-nál nagyobb szám kell. A számolás ellenőrzésére közöljük a megoldást, amely talán meglepő, de éppen a 4.
5. A játékelmélet további, iskolában is megmutatható alkalmazásai
Ehhez igen gazdag az irodalom, az első ilyen tárgyú munka a már említett Neumann és a közgazdász Morgenstern közös könyve [3]. Egy igazán gazdag tartalmú, didaktikailag is jól felépített és szerteágazó kapcsolatokat bemutató könyv Mérőtől származik [7]. Ebben kezdve a pszichológiától, viselkedés-lélektani, társadalmi és biológiai példák mellett a kvantummechanika ilyen szemléletű bemutatása is szerepel. Az evolúciós biológia területén Dawkins génekről írt könyve [8] tartalmazza annak leírását, hogy miként lehet az evolúció modellezésére ezt az elméletet sok esetben használni. Végül két, még az elmúlt század hetvenes éveiben a Műszaki Kiadónál megjelent könyvet említenénk meg, melyek közül a későbbi [10]-ben még irodalmi alkalmazásokat is olvashatunk, így Sherlock Holmes a híres detektív és a bűnöző Moriarty „párbaját a vonaton”. Méltánytalanul elfeledett, pedig akár középiskolás diákoknak is bátran ajánlható művekről van szó. Közülük a háromszerzős (egyikük Kemény János – már megint János! – magyar származású amerikai matematikus, aki a Basic nyelv kidolgozásával, Neumannhoz hasonlóan a számítástechnikában is jelentőset alkotott. Ő azonban a középiskolát már Amerikában járta ki, mivel az általános iskola elvégzése után zsidó származású szüleivel az Egyesült Államokba menekültek.) Ebben a könyvben [9], elsősorban diszkrét matematikát és valószínűségszámítási témákat dolgoznak fel, mátrixok komoly alkalmazásával. Mégis elemi tárgyalásmódja lehetővé teszi a matematikában kevésbé jártas olvasónak is a megértést, s egyben a modern matematika egyes elemeinek közérthető bemutatását nyújtja, kiváló példát mutatva a népszerűsítésre és a matematika szélesebb közönséghez eljuttatására. Egyben nagyon alkalmas tanárok számára is néhány az iskolában korábban nem szereplő téma egy lehetséges tárgyalására. Azért említem meg, mert a témánkhoz tartozó feladatokat is találhatunk benne.
6. Irodalom
[1] Staar Gy.: A megélt matematika – beszélgetések. Gondolat Kiadó Budapest 1990
[2] Neumann, J.: A kvantummechnika matematikai alapjai. Akadémiai Kiadó, Budapest 1980
[3] Morgenstern, O., von Neumann, J.: Theory of Games and Economic Behavior. University Press Princeton 2004 (Először 1944-ben jelent meg, mint a játékelmélet első monográfiája).
[4] Lovász, L.: Algoritmusok bonyolultsága. Egyetemi jegyzet, ELTE Matematikai Intézet A 2014-es változata elérhető: http://www.cs.elte.hu/~kiraly/alg.pdf
[5] Neumann, J.: Zur Theorie der Gesellschaftspiele. Mathematische Annalen, 100. 295– 320. (1928)
[6] Kóczy Á., L.: A Neumann-féle játékelmélet. Közgazdasági Szemle, LIII. évf., 2006. január (31–45. o.) online: http://epa.oszk.hu/00000/00017/00122/pdf/02koczy.pdf
[7] Mérő, L.: Mindenki másképp egyforma. Tercium Kiadó 2007
[8] Dawkins, R.: Az önző gén. Gondolat 1986
[9] Kemeny, Snell, Thompson: A modern matematika alapjai. Műszaki Kiadó 1971
[10] Williams J. D.: Játékelmélet. Műszaki Kiadó 1972
Vancsó Ödön,
ELTE TTK
Lábjegyzetek
1Lénárt István már nagyon sok iskolában elterjedt eszközéről a Lénárt gömbről lehet egy videót megnézni a http://lenartgomb.hu/ honlapon.
2 Régi játék, amelyet akárhányan játszhatnak. Mindenki 0 vagy 1 vagy 2 egyforma (pl. 5 forintos) pénzérmét tehet a kezébe. A kezdő mond egy számot a kezekbe levő összes pénzérmék számának becslésére, az utána következő hasonlóképpen, de az előző által mondott szám már foglalt. Ezt folytatva mindenki mond sorban egy számot, amely a megelőzőkétől különböző kell, hogy legyen. Az nyer, aki eltalálja a pénzdarabok számának összegét, ha ilyen nincs, akkor az, aki a legközelebbi egész számot mondta. A nyeremény a kezekben levő összes pénzdarab. Döntetlen esetén feleznek (ami akkor lép fel, ha pl. összesen 7 pénzdarab van a kezekben, ezt a számot senki nem mondta, de van 6 és 8 is tippként).
3Lásd pl. a Wikipédián: https://hu.wikipedia.org/wiki/Andrej_Nyikolajevics_Kolmogorov
4Kevert stratégia azt jelenti, hogy nem az egyiket vagy a másikat választom szisztematikusan, hanem, véletlen szerint „keverem” a választásomat minden egyes partiban. Az egyes stratégiákhoz tartozó valószínűségértékeknek van mindig optimális választása, erről szól a tétel.
5Róla még egy kiváló könyv és annak filmfeldolgozása is született „Egy csodálatos elme” címmel.








