Beszámoló a 10. fordulóról
Ebben a fordulóban 14-en küldtek válaszokat, megoldásokat, összesen 75 helyes választ. Nyolcan adtak mind a 7 feladatra hibátlan választ, és voltak, akik csak a 64-es feladatra küldtek választ és megoldást. A táblázat fejléce a feladatok számát mutatja, a színes cellák pedig a jó válaszokat.
Fordulónként a legjobb megoldók közül néhányan könyvjutalmat kapnak. A legújabb jutalmazottak Deli Lajos és Koncz Levente, ők a Matematikai Tehetségekért Alapítvány (korábban Zalamat) könyveit választották:
• Olosz Ferenc: Egyenletek I–II. kötet
• Ábrahám Gábor: Egyenlőtlenségek II.
Megoldások, megjegyzések a Héttusa 10. fordulójának feladataihoz
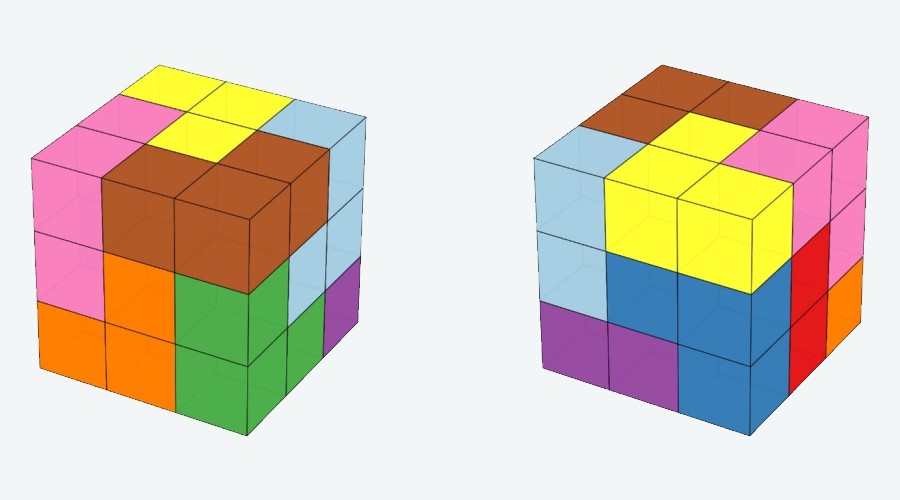
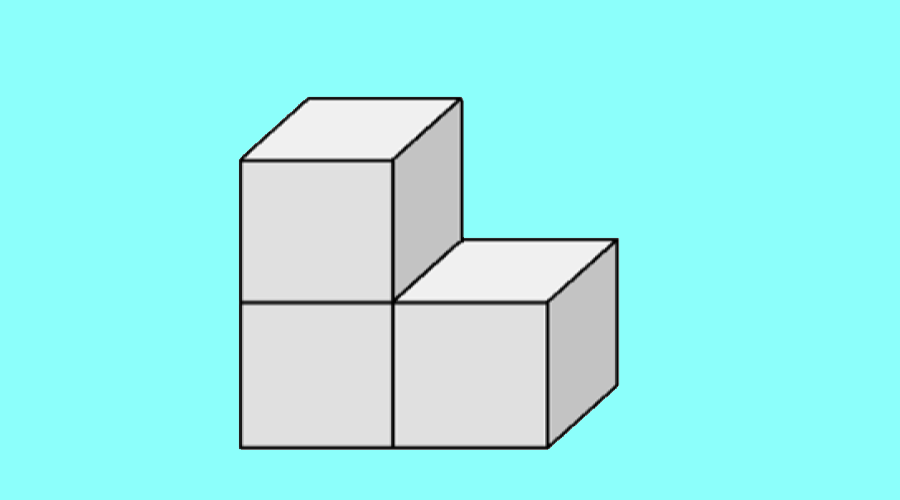
64. Megépíthető-e egy \(3\times3\times3\)-as kocka 9 db L-alakú testből? (Az L-alakú test három, az ábra szerint összeillesztett egységkockából áll.)
A válasz: Igen.
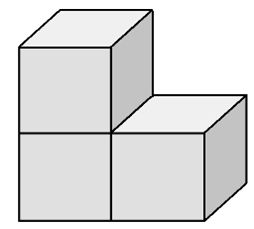
Szemerédi Ábris (6. osztályos) megoldása. Két L alakú idomból \(2\times3\times1\)-es panelt készítünk. 4 ilyen panelből megépíthetjük a \(3\times3\times3\)-as kocka falait, azaz a kockát úgy, hogy középen van egy függőleges lyuk.
Ha most egy panelt elveszünk, akkor a kockában meglévő üres helyet feltölthetjük 3 db L alakú idommal.
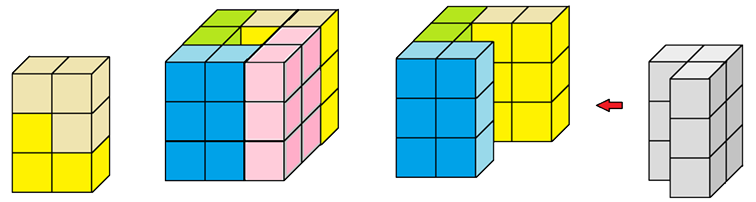
Dombi Péter mutatott olyan építést, amely nem tartalmaz \(2\times3\times1\)-es panelt. Ezt a kockát látjuk elölről és hátulról.
Az építést Turchányi Gyula egy GIF animációval mutatja, és az animációhoz a kódot az MI-vel íratta meg.
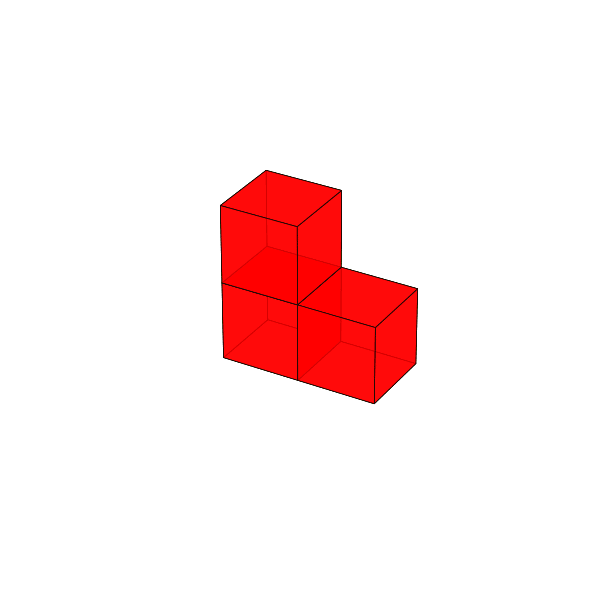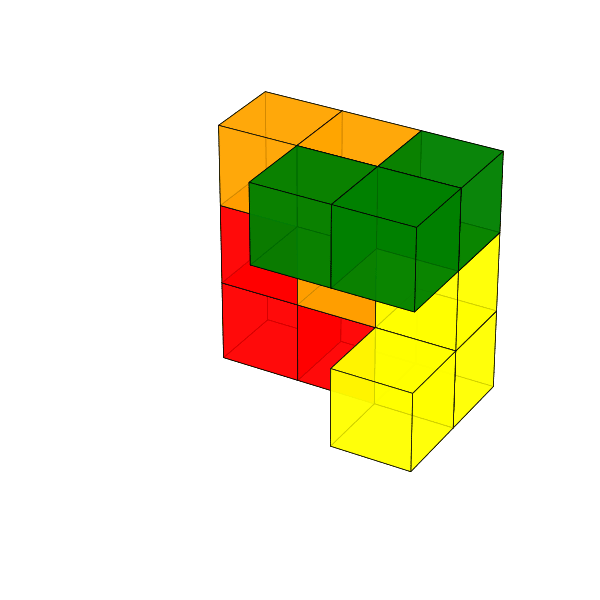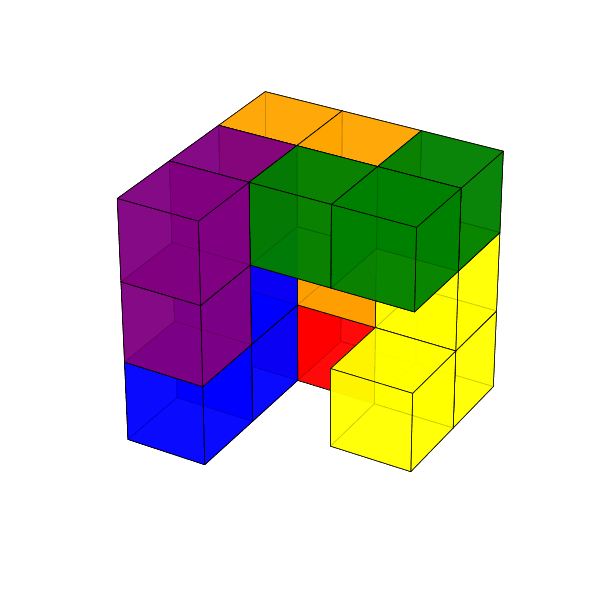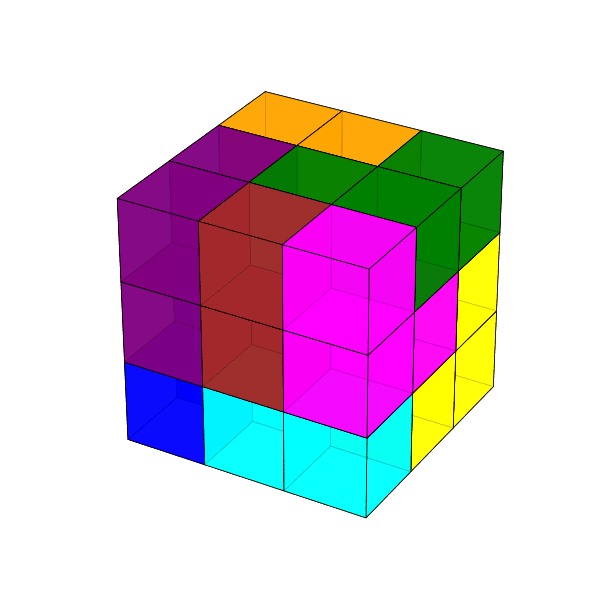
Az eredmény 3D-ben forgatva is elég jól láttatja a megoldást, egyedül a vörösesbarna darabnak a kocka közepébe nyúló része nem látszik.
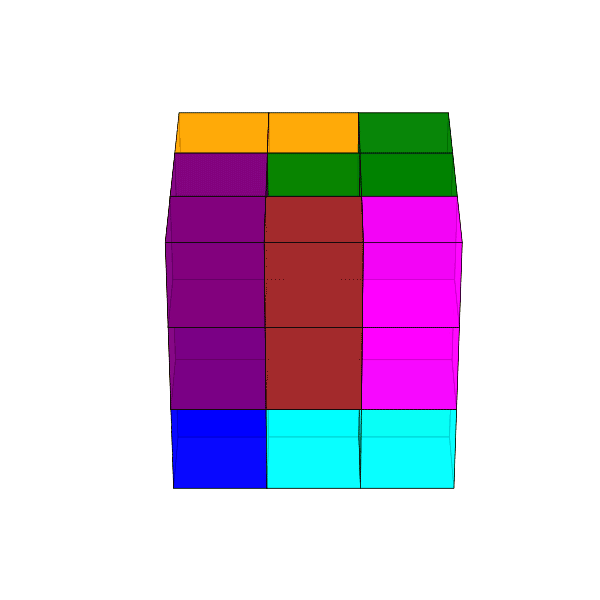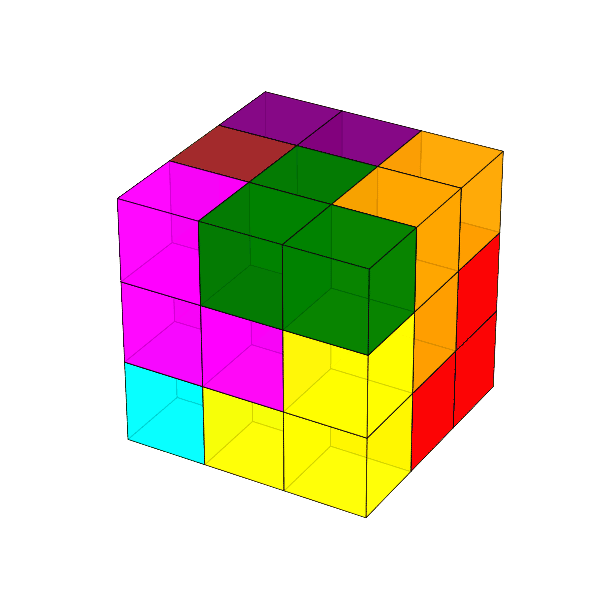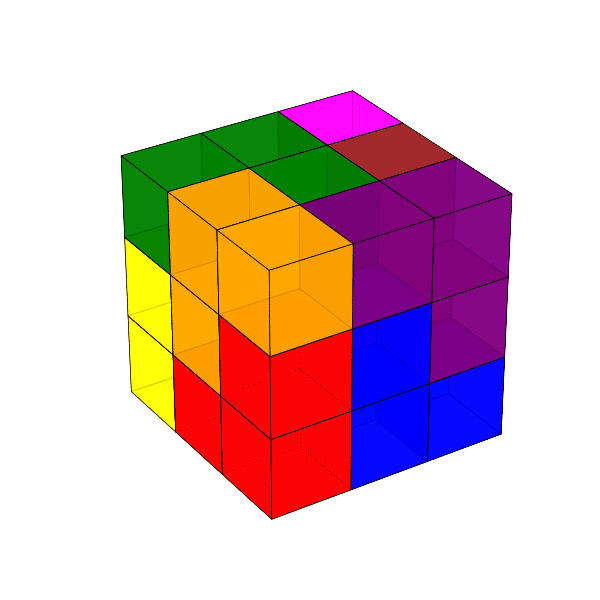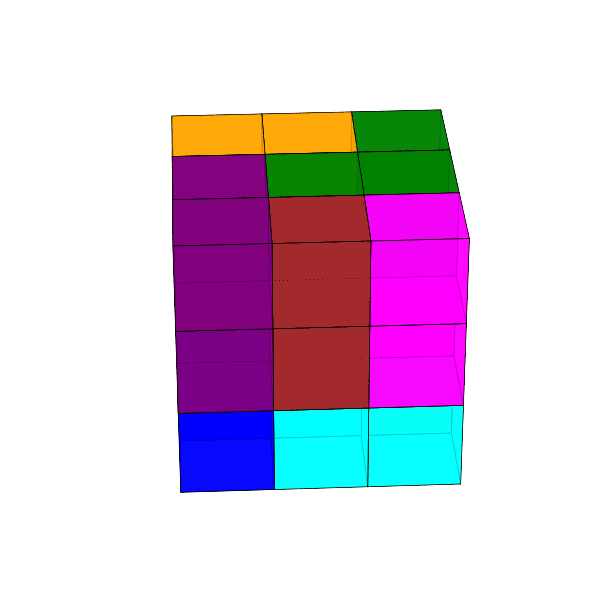
Megjegyzés. Alexander Soifer: Geometric Etudes in Combinatorial Mathematics (2. kiadás, New York, Springer, 2010) könyvében a 20.1. Tétel (Boltyanszkij–Soifer) szerint egy \(m\times n\times k\) méretű tégla pontosan akkor építhető meg L-alakú testekből (azaz trominókból), ha \(m\cdot n\cdot k\) osztható 3-mal.
65. Adott a síkon 7 különböző pont, közülük 6 egy egyenesre esik. Tekintsük azokat a háromszögeket, amelyeknek csúcsait ezen pontok közül választjuk. Legfeljebb hány egyenlő szárú háromszög lehet a háromszögek között?
A válasz: 9.
Megoldás. A hetedik pont – amely nem illeszkedik a többi 6 pont által felfeszített egyenesre – csúcsa lesz a kiválasztható egyenlő szárú háromszögeknek. Vagy ,,hegycsúcs”, azaz a két egyenlő szár közös csúcsa; vagy ,,sarokcsúcs”, azaz az egyenlő szárú háromszög alapján fekszik.
A hetedik pontot hat szakasz köti össze a többi ponttal, ezért 3 egyenlő szárú háromszögben lehet hegycsúcs.
A hetedik pont 6 háromszögben lehet sarokcsúcs, hiszen ha öszekötjük a hat pont valamelyikével, ez a szakasz lesz majd a háromszög alapja, és erre az alapra legfeljebb egy egyenlő szárú háromszöget építhetünk.
Ezért legfeljebb \(3+6=9\) egyenlő szárú háromszög lehet a háromszögek között.
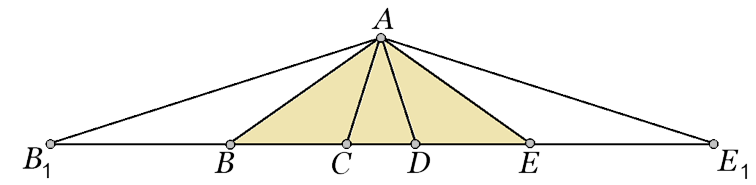
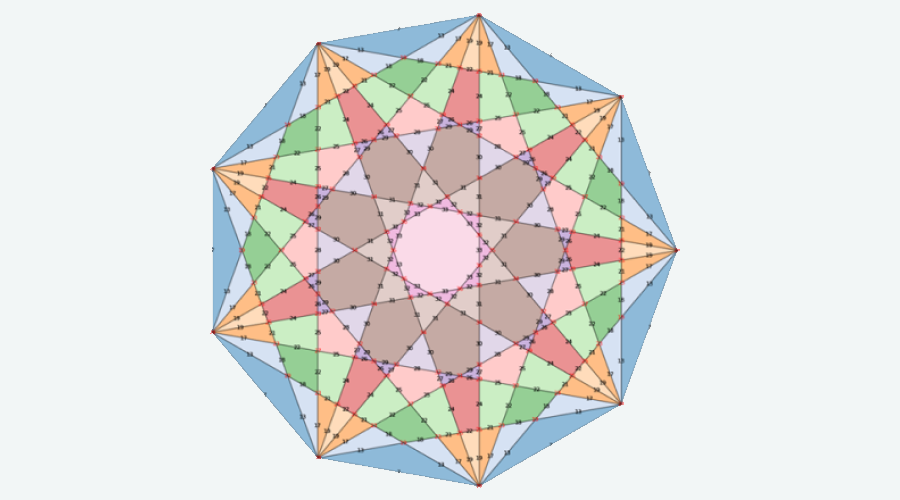
Az ábra befestett része egy szabályos ötszög ,,felső része”, amelybe behúztuk az átlókat.
Az \(ACD\) háromszög szögei \(72^{\circ}\), \(72^{\circ}\), \(36^{\circ}\), és \(BC=CA=AD=DE\), továbbá \(BA=BB_1=EA=EE_1\).
Az ábrán látjuk azt a 3 háromszöget, amelyben \(A\) hegycsúcs, és azt a 6 háromszöget, ahol \(A\) sarokcsúcs, összesen 9 egyenlő szárú háromszöget.
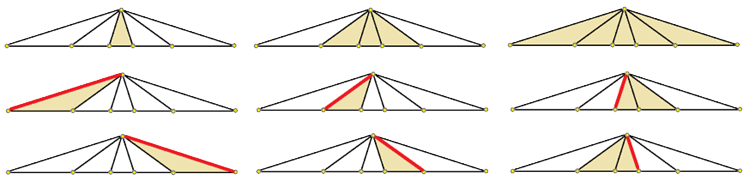
Dombi Péter írja a megoldásában, hogy a minta természetesen folytatható, így azt kapjuk, hogy \(2m+1\) olyan pont közül, amelyekből \(2m\) kollineáris, legfeljebb \(3m\) egyenlő szárú háromszög választható ki.
Berkó Erzsébet megoldásában az \(ACD\) háromszög szögei \(80^{\circ}\), \(80^{\circ}\), \(20^{\circ}\), és a többi pontot az előbbi mintázat szerint veszi fel. Az előbbihez képest a 6 sarokcsúcsos háromszög részben másképp jelenik meg, mint az előbbi esetben.

66. Egy \(5\times5\)-ös táblázat minden cellájába beírtunk egy-egy egész számot. A táblázat két sora és két oszlopa a közös mezőkkel kijelöli egy téglalap négy csúcsát. Minden ilyen téglalapban kiszámoljuk a sarokmezőkben álló négy szám összegét. Legfeljebb hány esetben lesz ez az összeg páratlan?
A válasz: 60.
Megoldás. Válasszunk két sort, és oszloponként számoljuk ki annak a két számnak az összegét, amelyek ebben az oszlopban és a választott két sorban vannak. Öt ilyen összeget kapunk, \(a\) esetben páros, és \(b\) esetben páratlan az összeg, ezekre \(a+b=5\).
Nézzük a téglalapokat, amelyeknek a sarokmezői ebben a két sorban vannak. \(a\cdot b\) olyan téglalap van, amikor a sarokmezőkben álló számok összege páratlan. Mivel \(a\cdot b\le6\), emiatt egy sorpárhoz tartozó téglalapok között legfeljebb 6 páratlan összegű téglalap van.
\(\binom{5}{2}=10\) sorpár van, ezért az \(5\times5\)-ös táblázatban legfeljebb \(10\cdot6=60\) páratlan összegű téglalap van.
Van olyan táblázat, amelyben a páratlan összegű téglalapok száma 60. A táblázat egyik átlójába írjunk 1-eseket, a többi mezőbe 0-t. Ekkor egy páratlan összegű téglalap egyik sarkában 1 áll, a többiben 0. Az ilyen téglalapok száma \(5\cdot12=60\).
Deli Lajos megoldása:
Induljunk ki abból a helyzetből, hogy minden cellába páros számot írtunk – ekkor minden összeg páros. Pontosan 100 összegről beszélünk, mert az öt sorból és az öt oszlopból 10-féleképpen választható ki kettő-kettő, és \(10\cdot10=100\).
Cseréljük le az egyik cellában (bármelyikben) a páros számot páratlanra. Ha ez a cella egy kijelölt téglalap egyik csúcsa, a vele szemközti csúcs \(25-9=16\)-féleképpen választható meg (a saját sorából és oszlopából szemközti csúcs nem választható). Ebben a 16 téglalapban a csúcs-összeg páratlan, mert a négy szám közül egy páratlan és három páros.
Nézzük, mi történik, ha újabb páros számot cserélek páratlanra (megtartva az előzőt). Két esetet különböztetek meg:
-
- Ez a második páratlan szám nincs az első páratlan számmal egy sorban vagy egy oszlopban. Ekkor egyetlen téglalap két átlós celláját alkotják, ebben a téglalapban az összeg páros, minden más esetben páratlan. \(2\cdot(16-1)=30\) páratlan összeg lesz.
- Ha a második páratlan szám egy sorba vagy egy oszlopba esik az első páratlan számmal, akkor \(2\cdot12=24\) páratlan összeg lesz, mert annál a négy téglalapnál, melynek ezek a páratlan cellák szomszédos csúcsai a csúcs-összeg páros lesz.
A leírtak miatt további páratlan számokat olyan cellákban kell becserélni, amelyek nincsenek egy sorban vagy egy oszlopban korábban elhelyezett páratlan számmal, és csak addig mehet az eljárás, amíg ez teljesíthető. Ez azt jelenti, hogy 5 cellába kerül páratlan szám, amelyek minden sort és oszlopot ,,lefednek” (például az egyik átló öt cellájába), és így \(5\cdot(16-4)=60\) páratlan összeg lesz.
67. A síkon adott 20 különböző pont, amelyek között nincs három egy egyenesre eső. Igaz-e, hogy a pontok párosíthatók úgy, hogy a párba állított pontokat összekötő 10 szakasz mindegyike metszi a többi szakaszt?
A válasz: Nem igaz.
Megoldás. Vegyünk fel 19 pontot egy körön, egyenletesen elrendezve. Jelöljük őket sorban az 1, 2, …, 19 számokkal. A huszadik pont a kör közepe. A kör közepét összeköti egy szakasz a 19 pont valamelyikével. Legyen ez az 1-es.
A 10-est bármelyik másikkal kötjük össze, az nem metszi a kör közepéből induló szakaszt.
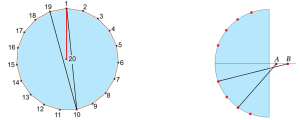
Udvari Tibor példája is páros sok különböző pontra mutat példát, ahol nincs olyan párosítás, amikor az összekötő szakaszok közül bármely kettő metszené egymást. Az \(AB\) egyenes a pontrendszernek szimmetriatengelye. Az \(AB\) szakaszt egyetlen további behúzható szakasz sem metszi, ezért nem lehetnek egymással összekötve. Ha az \(A\) pont például az \(AB\) egyenes alatti pontok közül van az egyikkel összekötve, akkor a \(B\) pontot is azok egyikével kell összekötni, hogy a két szakasznak legyen metszéspontja. Ekkor viszont az \(A\)-t tartalmazó szakasz egyik oldalán több pont marad, mint a másikon, így lesz ezen az oldalon két egymással összekötött pont. Az ezek által meghatározott szakasz pedig biztosan nem metszi az \(A\)-ból húzott szakaszt. Tehát nem tudjuk biztosítani, hogy mindegyik szakasz metssze az összes többit.
Dombi Péter szerint az állítás abban a gyengébb formában sem igaz, hogy mindegyik szakasz messe a többi szakasz valamelyikét. Legyen \(f(x)\) egy szigorúan konvex és szigorúan monoton növő függvény a \([0,1]\) intervallumon, például legyen \(f(x)=x^2\). Vegyük fel egy kivételével az összes pontot a függvénygörbén, azaz legyen \[P_i=(x_i; x_i^2), \qquad 0<x_1<x_2<\dots<x_{19}<1,\] és legyen \(P_0=(1; 0)\). Ekkor \(P_0\)-hoz akárhogy társítunk egy \(P_k\) pontot, a \(P_k P_0\) szakasz teljes egészében a függvénygörbe alatt marad, ugyanakkor mindegyik \(P_i P_j\) szakasz (\(i\), \(j \ne0\)) a konvexitás miatt a függvénygörbe felett halad, ezért egyik sem metszheti a \(P_k P_0\) szakaszt.
Megjegyzés. Más, hasonló kérdések is feltehetők. (Várhatóan lesz is ilyen kérdés a következő fordulóban.)
Ez a cikk Erdős–Szekeres típusú kérdést vizsgál:
https://ematlap.hu/wp-content/uploads/2025/12/67-aksv-crossfam-eurocg21.pdf
A síkon \(n\) pont általános helyzetű, ha nincs közte három, melyek egy egyenesre esnek. Ilyen ponthalmazban kiválasztunk két-két pontot és azokat összekötjük szakasszal. Ezen szakaszok közül \(k\) szakasz metsző családot alkot, ha bármely kettő metszi egymást. A cikk bebizonyítja, hogy bármely legalább 15 pontból álló halmazban találunk 4 szakaszból álló metsző családot.
Bizonyítja azt is, hogy bármely \(n\)-re van olyan \(n\) pontból álló halmaz, amelyben nincs \(4\lceil\frac{n}{20}\rceil\)-nál több szakaszból álló metsző család.
68. Az 1, 2, …, 20 számokat egymás után írtuk valamilyen sorrendben. Igaz-e, hogy a számok 6 lépésben nagyság szerint növekvő sorrendbe rendezhetők, ha egy-egy lépésben kiválasztunk 10 egymás után sorakozó számot, és ezek sorrendjét tetszőleges módon átrendezhetjük?
A válasz: Igaz.
Koncz Levente megoldása. Hat lépésben mindig sorbarendezhetők a számok.
-
- Az 1–10. helyen levő számok közül mozgassuk a 6–10. helyek valamelyikére az összes 16–20 közötti számot.
- A 11–20. helyen levő számok közül mozgassuk a 11–15. helyek valamelyikére az összes 1–5 közötti számot.
- A 6–15. helyen levő számok között cseréljük fel az első ötöt a második öttel. Így az 1–5 közötti számok mind az 1–10. helyek valamelyikére, a 16–20 közötti számok a 11–20. helyek valamelyikére kerültek.
- Az 1–10. helyen levő számok közül mozgassuk a helyükre az 1–5 közötti számokat.
- A 11–20. helyen levő számok közül mozgassuk a helyükre a 16–20 közötti számokat.
- Mozgassuk a helyükre a 6–15. helyen levő számokat.
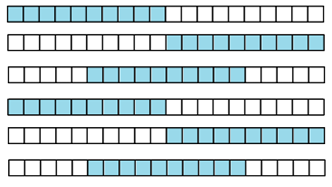
Dombi Péter megmutatta, hogy általánosan is igaz az állítás: Ha \(n\) páros, akkor minden \(n\) elemű permutáció (lista) 6 lépésben átrendezhető úgy, hogy minden lépésben \(n\!⁄\!2\) számú egymás után következő elemét rendezzük sorba.
A lépéssorozat csak \(n\) értékétől függ, és azonos felépítésű a 4-gyel osztható \(n\)-ekre, és ugyancsak azonos felépítésű az \(n=4m+2\) alakúakra is.
69. Egy körön kijelöltünk 100 különböző pontot, és ezekhez odaírtuk az 1, 2, …, 100 számokat valamilyen sorrendben. Igaz-e, hogy a számok párosíthatók úgy, hogy a párba állított számok összege páratlan, és a hozzájuk tartozó pontokat összekötő 50 szakasz nem metszi egymást?
A válasz: Igaz.
Megoldás. Az a lényeges, hogy egy a feladatban szereplő szám páros, vagy páratlan. Helyettesítsük a páros számokat 0-val, a páratlan számokat 1-gyel.
Nézzük meg kicsiben, 100 helyett kisebb páros számokra. 2-re, 4-re igaz az állítás. Bizonyítsunk teljes indukcióval. Feltehetjük, hogy valamely \(n\)-re még igaz, \(n\) db 0 és \(n\) db 1-es esetén van megfelelő párba állítás, összekötés. Ha a körön most \((n+1)\) db 0 és \((n+1)\) db 1-es van, találunk köztük két szomszédos különböző számot. Először ezt az 1-et és 0-t kössük össze szakasszal. A többi \(n\) db 0 és \(n\) db 1-es esetén az indukciós feltevés miatt van megfelelő összekötés, és ezek a szakaszok nem metszik az elsőként megrajzolt szakaszt.
Izsák Beatrix rövid indoklása: Itt mindig a szomszédos ellenkező paritású pontokat kössük össze, majd a maradék pontokat tekintsük és ott is folytassuk, amíg készen nem leszünk.
70. Egy \(4\times4\)-es táblázat celláiba beírtuk az 1, 1, 2, 2, …, 8, 8 számokat. Igaz-e, hogy mindig választhatunk 8 cellát úgy, hogy minden sorban és minden oszlopban legyen legalább egy kiválasztott cella, és a cellákban különböző számok szerepeljenek?
A válasz: Igaz.
Megoldás. Összesen \(2^8\) lehetőség van az 1, 2, …, 8 számokat tartalmazó 8 cella kiválasztására. Becsüljük meg a rossz választások számát. Ha az első oszlopból nem választunk számot, akkor ott nem lehet két egyforma szám, tehát az itteni 4 számnak a másik példányát kell választani, majd a többi \(8-4=4\) számból egyet-egyet, ez \(2^4\) lehetőség. A ,,hibás” sort vagy oszlopot \(4+4=8\)-féleképp választhatjuk, így a rossz választások száma legfeljebb \(8\cdot2^4\), és ez a szám kisebb \(2^8\)-nál, így van jó választás is.
Szemerédi Ferenc megoldása:
Elég kiválasztani 4 cellát úgy, hogy minden sorban és minden oszlopban pontosan egy kiválasztott cella legyen és a cellákban különböző számok szerepeljenek. Ha ez megtörtént, ezek mellé a 4 hiányzó számot tartalmazó cellát választva a feladatnak megfelelő kiválasztást kapunk.
Van-e 4 ilyen független cella négy különböző számmal?
Négy független cellát (ha minden sorból és minden oszlopból pontosan egy cellát választunk) \(4\cdot3\cdot2\cdot1=24\) féleképp adhatunk meg, ezeket nevezzük helyzetileg jó kiválasztásnak. Ezek közül nem megfelelő az, amiben két 1-es, vagy két 2-es, …, vagy két 8-as szerepel. Két 1-es legfeljebb 2 db helyzetileg jó kiválasztást ronthat el (azokban a másik két cella az 1-est nem tartalmazó két sorban és két oszlopban van, ez kétféleképpen lehetséges). A 8 db szám így legfeljebb \(8\cdot2=16\) kiválasztást ront el, emiatt legalább \(24-16=8\) olyan van, ami helyzetileg jó, és a számok különbözőek.
Ha a \(4\times4\)-es táblázatban találunk 4 független cellát különböző számokkal, abból következik a feladat állítása. Fordítva is igaz, ha a táblázatban megtaláljuk a kívánt 8 cellát, akkor azokból kijelölhetünk 4 független cellát, különböző számokkal. Erről szól az 1981-es Kürschák-verseny egyik feladata:
Legyen \(n\) 2-nél nagyobb páros szám. Egy \(n\times n\)-es sakktábla mezőit kiszínezzük \(n^2/2\) színnel úgy, hogy minden színű mezőből pontosan kettő van. Bizonyítsuk be, hogy el lehet helyezni \(n\) bástyát csupa különböző színű mezőre úgy, hogy semelyik kettő se üsse egymást.
Dombi Péter is ezt az utat járja.
Elég azt igazolni, hogy van négy független cella, ahol különböző számok vannak, hiszen ezeket tetszőlegesen kiegészíthetjük négy másik reprezentánssal. Nem jelent többletmunkát ezt az állítást 4 helyett \(n\)-re bizonyítani, a következő formában.
Állítás. Ha egy \(n\times n\)-es táblázatban (\(n>2\)) minden elem legfeljebb 2-szer fordul elő, akkor kiválasztható \(n\) darab független cella különböző elemekkel.
Bizonyítás. Egy \(n\times n\)-es táblázatban az összes független \(n\)-esek (transzverzálisok) száma \(n!\). Tekintsük azokat az elemeket, amik legalább – és így pontosan – kétszer fordulnak elő, ezek száma a feltétel szerint legfeljebb \(\lfloor n^2⁄2\rfloor\). Egy ilyen elempár \((n-2)!\) transzverzálist blokkol, ha két független cellában fordul elő, és persze 0-t, ha ugyanabban a sorban vagy oszlopban fordul elő, ezért az ismétlődő elemek összesen legfeljebb \(\lfloor n^2⁄2 \rfloor \cdot(n-2)!\) transzverzálist tudnak elrontani. Elég tehát belátni, hogy ez a szám kisebb, mint \(n!\), hiszen akkor biztosan van olyan transzverzális, amit egyik ismétlődő elem sem tud elrontani. Az igazolandó egyenlőtlenség \((n-2)!\)-sal való egyszerűsítés után \[\Big\lfloor \frac{n^2}2\Big\rfloor<n(n-1)\] alakú, ami még egészrész nélkül is igaz, hiszen \(n^2<2n(n-1)\), azaz \(n(n-2)>0\), hacsak \(n>2\). Az utóbbi feltételre valóban szükség van, ezt mutatja a \(\begin{pmatrix} 1 & 2 \\ 2 & 1 \\ \end{pmatrix}\) mátrix.
Többen sor- és oszlopcserékkel rendezték a táblázatot úgy, hogy ezután a főátlóban különböző számok álljanak.
Megjegyzés. A feladatra – egy \(8\times8\)-as táblázatba az 1, 2, 3, …, 32 számokat írjuk, mindegyiket kétszer, és választani kell a 32 szám mindegyikéből egyet, hogy legyen köztük 8 független cella – 2016-ban a Kvant folyóirat egyik cikke 7 különböző megoldást adott: https://kvant.ras.ru/pdf/2016/2016-02.pdf
Róka Sándor, a Héttusa rovet vezetője