A Héttusa rovatban kitűzött feladatokra bárki küldhet megoldást. Ehhez a feladatok sorszámát és a feltett kérdésekre a válaszokat kell megküldeni, indoklást, részletes megoldást nem szükséges írni.
A válaszokat a hettusa@ematlap.hu címre várjuk. A beküldési határidő: 2025. október 6.
A verseny nyilvántartása érdekében kérjük, hogy megoldásaikat névvel vagy olyan álnévvel írják alá, amit nyilvánosan közzé tehetünk.
A határidőt követően a megoldások megjelennek a Facebook-oldalunkon. Az ezután beküldött megoldásokat nem értékeljük a versenyben. A Héttusa rovatban a megoldások értékelése után olvashatják a legjobb megoldók nevét és a megjegyzéseket, kiegészítéseket a megoldásokhoz.
Versenyzőinket két kategóriában jutalmazzuk: diák (általános vagy középiskolás), illetve felnőtt. Kérjük, hogy beküldéskor jelezzék, melyik kategóriában indulnak. Ha valaki ezt nem jelzi, őt a felnőttek közé soroljuk.
Fordulónként a legjobb megoldók közül néhányan könyvjutalmat kapnak.
A Héttusába bekapcsolódók a KöMaL honlapján a Fórum rovatban megoszthatják egymással gondolataikat, ötleteiket a feladatokról, bíztatjuk versenyzőinket, használják ki ezt a lehetőséget is.
Feladatrovatunkhoz örömmel veszünk minden segítő szándékot, várjuk új feladatjavaslataikat, valamelyik feladat szép megoldását, vagy a feladat általánosítását.
A 10. forduló feladatai
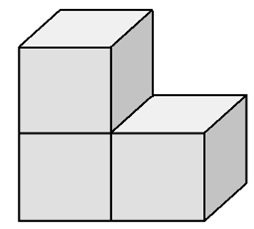
64. Megépíthető-e egy \(3\times3\times3\)-as kocka 9 db L-alakú testből? (Az L-alakú test három, az ábra szerint összeillesztett egységkockából áll.)
65. Adott a síkon 7 különböző pont, közülük 6 egy egyenesre esik. Tekintsük azokat a háromszögeket, amelyeknek csúcsait ezen pontok közül választjuk. Legfeljebb hány egyenlő szárú háromszög lehet a háromszögek között?
66. Egy \(5\times5\)-ös táblázat minden cellájába beírtunk egy-egy egész számot. A táblázat két sora és két oszlopa a közös mezőkkel kijelöli egy téglalap négy csúcsát. Minden ilyen téglalapban kiszámoljuk a sarokmezőkben álló négy szám összegét. Legfeljebb hány esetben lesz ez az összeg páratlan?
67. A síkon adott 20 különböző pont, amelyek között nincs három egy egyenesre eső. Igaz-e, hogy a pontok párosíthatók úgy, hogy a párba állított pontokat összekötő 10 szakasz mindegyike metszi a többi szakaszt?
68. Az 1, 2, …, 20 számokat egymás után írtuk valamilyen sorrendben. Igaz-e, hogy a számok 6 lépésben nagyság szerint növekvő sorrendbe rendezhetők, ha egy-egy lépésben kiválasztunk 10 egymás után sorakozó számot, és ezek sorrendjét tetszőleges módon átrendezhetjük?
69. Egy körön kijelöltünk 100 különböző pontot, és ezekhez odaírtuk az 1, 2, …, 100 számokat valamilyen sorrendben. Igaz-e, hogy a számok párosíthatók úgy, hogy a párba állított számok összege páratlan, és a hozzájuk tartozó pontokat összekötő 50 szakasz nem metszi egymást?
70. Egy \(4\times4\)-es táblázat celláiba beírtuk az 1, 1, 2, 2, …, 8, 8 számokat. Igaz-e, hogy mindig választhatunk 8 cellát úgy, hogy minden sorban és minden oszlopban legyen legalább egy kiválasztott cella, és a cellákban különböző számok szerepeljenek?
A feladatokat válogatta: Róka Sándor, a Héttusa rovat vezetője