1. Bevezető
A híres Fibonacci-sorozat évszázadok óta magával ragad matematikusokat, művészeket, tervezőket és tudósokat. A Fibonacci-sorozat kezdő tagjai a következők: \[\displaystyle F_0=0,\qquad F_1=1,\qquad F_2=1,\qquad F_3=2,\qquad F_4=3,\qquad F_5=5,\qquad \dots\] és definiciója rekurzívan adható meg a következő módon:
| \(\displaystyle F_n=F_{n-1}+F_{n-2},\qquad n >1.\) | (1) |
A Lucas-számokból álló sorozat ugyanezzel az (1) rekurzív képlettel adható meg, de a kezdő tagja eltér a Fibonacci-sorozatétól. Így a Lucas-számok sorozatának első néhány tagja: \[\displaystyle L_0=2,\qquad L_1=1,\qquad L_2=3,\qquad L_3=4,\qquad L_4=7,\qquad L_5=11,\qquad \dots\]
A Fibonacci-számsorozatot alaposan tanulmányozták és több példa van arra, hogy a természetben felfedezhetők olyan jelenségek, amelyekben ennek a számsorozatnak a tagjai megjelennek. A 2. fejezetben bemutatjuk, hogy a méhek családfájában megfigyelhető az (1) rekurzió. Ezt Fibonacci, Leonardo da Pisa (1170–1250) olasz matematikus is tanulmányozta. A 3. fejezetben a Fibonacci-sorozat tagjait megadó explicit formulát, a Binet-formulát vezetjük le, ami kapcsolatot teremt a sorozat és az aranymetszés arányszáma között. Továbbá levezetünk néhány olyan összefüggést a Fibonacci-sorozat és a Lucas-számokból álló sorozat tagjai között, amelyet alkalmazni fogunk a 4. fejezetben. A 4. fejezetben egy geometriai kapcsolatot mutatunk be a Fibonacci-sorozat és a Lucas-számokból álló sorozat között.
2. A Fibonacci-sorozat és a méhek családfája
A Fibonacci-sorozatot önmagában is különlegesen érdekes tanulmányozni, ugyanakkor rádöbbent annak a világnak az összetettségére és rendjére, amelyben élünk ([4]). Amikor Fibonaccit megkérdezték, hogy miért vizsgálja ezeket a számokat és a hányadosukat, ő ezt válaszolta: „Egy napon ezek a számok felfedik a természet titkát és érthetővé teszik, hogy egy hím méhnek miért nincs apja” ([2]). A hím méhek ugyanis a megtermékenyítetlen petesejtekből kelnek ki. Ezzel ellentétben a nőstény méhek – amelyek lehetnek anyaméhek, azaz királynők, vagy dolgozók – a hímek által megtermékenyített petesejtekből jönnek a világra. Az 1. ábra a méhek érdekes családfáját mutatja be.
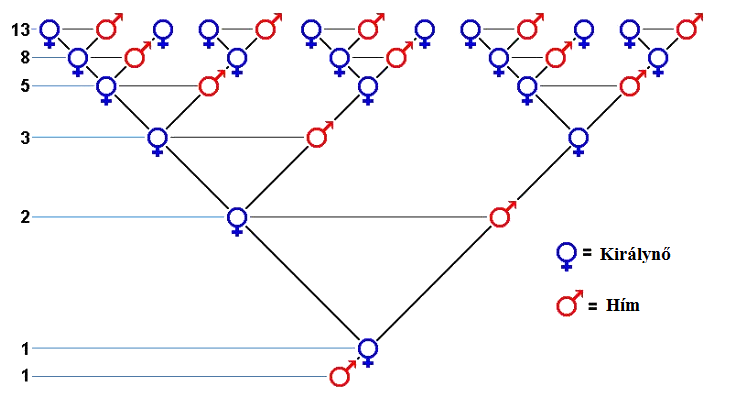
Az ábra egy kiválasztott hím méh felmenőinek számát szemlélteti. Az ábrán alul, a 0. generációs szinten van a kiválasztott hím. Neki csak anyja van, egy nőstény méhkirálynő, az 1. generációban. Ennek a nőstény méhnek két szülője van, egy hím méh és egy nőstény méhkirálynő. Ők találhatók a 2. generációs szinten. Ők ketten a kiválasztott hím méh nagyszülei. A 2. generációs szinten álló nőstény méhkirálynőnek, két szülője van, míg ezen a szinten a hímnek csak egy (a királynő), így két nőstény méh és egy hím méh áll a 3. generációs szinten, és így tovább (lásd [5]). A méhek családfája egyedülálló, hiszen mind a méhkirálynők mind pedig a hímek generációiban a Fibonacci-sorozat tagjai szerepelnek. Jelölje \(K_n\), illetve \(H_n\) az \(n\)-ik generációban a méhkirálynők, illetve a hím méhek számát, ha \(n > 0\). Legyen \(K_0=0\), \(H_0=1\). Ekkor az \((n+1)\)-ik generációban a méhkirálynők száma, illetve a hím méhek száma
| \(\displaystyle K_{n+1}=K_n+H_n,\qquad\) illetve \(\displaystyle \qquad H_{n+1}=K_n.\) | (2) |
Mivel a (2) második egyenlőségéből tudjuk, hogy \(H_n=K_{n-1}\), így az első egyenlőségből azt kapjuk, hogy \(K_{n+1}=K_n+ K_{n-1}\), azaz a méhkirálynők számára az (1) rekurzió érvényes. Mivel \[\displaystyle H_{n+1}=K_n=K_{n-1}+H_{n-1}=H_{n}+H_{n-1},\] ezért \(n \ge 1\)-től az egymást követő generációs szinteken a hím méhek száma is a Fibonacci-számok sorozata szerint növekszik.
3. A Binet-formula
A Fibonacci-sorozat a matematikában az egyik legismertebb másodrendben rekurzív sorozat. Tekintsük egy mértani sorozatot, jelölje \(a_1\) a sorozat első tagját és \(q\) a hányadosát. A sorozat \(n\)-edik tagját az \(a_n=a_1 q^{n-1}\) összefüggés adja meg. Határozzuk meg, hogy milyen \(q\) esetén kapunk Fibonacci-sorozatot, azaz milyen \(q\) esetén teljesíti egy mértani sorozat az (1) rekurziós képletet ([3]). Ekkor igaz, hogy \[\displaystyle a_{n}=a_{n-1}+a_{n-2},\] azaz \[\displaystyle a_1 q^{n-1}=a_1 q^{n-2}+a_1 q^{n-3}.\]
Ha \(a_1 \neq 0\), \(q \neq 0\), akkor egyszerűsítés után a
| \(\displaystyle q^2=q+1\) | (3) |
másodfokú egyenletet kapjuk, amelynek két irracionális valós gyöke van: \(\alpha :=\frac{1+\sqrt{5}}{2}\), ami a híres aranymetszés arányszáma, és \(\beta :=\frac{1-\sqrt{5}}{2}\). A [6] forrás alapján a Fibonacci-sorozat és az aranymetszés közötti kapcsolat Kepler egy 1608-ban írt levelében szerepelt, illetve már a 16. század elején ismert volt.
Jacques Philippe Marie Binet (1786–1856) francia matematikus a Fibonacci-sorozat tagjaira egy explicit formulát adott. Felhasználva a \(q^2=q+1\) összefüggést \(q\) hatványaira, azt nyerjük, hogy \[\begin{align} q^3&=q \cdot q^2=q(q+1)=q^2+q=q+1+q=2q+1\\ q^4&=q(2q+1)=2q^2+q=2(q+1)+q=3q+2\\ q^5&=q(3q+2)=3q^2+2q=3(q+1)+2q=5q+3\\ q^6&=q(5q+3)=5q^2+3q=5(q+1)+3q=8q+5.\end{align}\]
3.1. Lemma. Tetszőleges \(n\) pozitív egészre \(q^n=F_n \cdot q+F_{n-1}\).
Bizonyítás. A bizonyítást teljes indukció alkalmazásával végezzük el. \(n=1\) esetén a \(q=q\) azonosságot kapjuk. \(n=2\) esetén a \(q^2=q+1\) összefüggéshez jutunk. Tegyük fel, hogy \(n=k\)-ra igaz az állítás, azaz teljesül, hogy \(q^k=F_k \cdot q+F_{k-1}\). Ekkor \[\displaystyle\begin{align}q^{k+1}&=q \cdot q^k=q(F_k \cdot q+F_{k-1})=F_k \cdot q^2+F_{k-1} \cdot q=\\ &=F_k(q+1)+F_{k-1} \cdot q=(F_k+F_{k-1})q+F_k=F_{k+1} \cdot q+F_k.\end{align}\] Ezzel megkaptuk az állítást \(n=k+1\) esetén. Ez bizonyítja a lemmát. □
Mivel \(\alpha\) és \(\beta\) megoldása a (3) másodfokú egyenletnek, ezért a 3.1. Lemma miatt igaz, hogy \[\displaystyle \alpha^n=F_n \alpha+F_{n-1}, \quad \beta^n=F_n \beta+F_{n-1}.\] A második egyenlet kivonása az első egyenletből a következő eredményt adja: \[\displaystyle \alpha^n- \beta^n=F_n(\alpha -\beta).\] Mivel \(\alpha -\beta=\sqrt{5} \) ebből adódik a Binet-formula:
| \(\displaystyle F_n=\frac{1}{\sqrt{5}}(\alpha^n-\beta^n).\) | (4) |
A következő lemma analóg összefüggést ad a Lucas-számokból álló sorozat tagjai valamint az \(\alpha\) és \(\beta\) számok között ([1], Lemma 3.3.2, p. 14).
3.2. Lemma. Minden \(n \ge 0\) esetén teljesül, hogy \(L_n=\alpha^n+\beta^n\).
Bizonyítás. A bizonyítást teljes indukcióval végezzük el. Ha \(n=0\), akkor \(L_0=\alpha^0+\beta^0=1+1=2\). Ha \(n=1\), akkor \(L_1=\alpha^1+\beta^1=1\).
Tegyük fel, hogy \(n=k\) esetén igaz az \(L_k=\alpha^k+\beta^k\) összefüggés. Belátjuk, hogy \(n=k+1\)-re is érvényes, azaz \(L_{k+1}=\alpha^{k+1}+\beta^{k+1}\) teljesül. Felhasználva az (1) rekurziót, azt kapjuk, hogy:
| \(\displaystyle L_{k+1}=L_k+L_{k-1}=\alpha^k+\beta^k+\alpha^{k-1}+\beta^{k-1}=\alpha^k (1+\alpha^{-1})+\beta^k (1+\beta^{-1}).\) | (5) |
Mivel \(\alpha\) és \(\beta\) megoldásai a (3) egyenletnek, ezért \(\alpha^2=\alpha+1\), illetve \(\beta^2=\beta+1\). Osztva \(\alpha\)-val, illetve \(\beta\)-val rendezés után nyerjük, hogy
| \(\displaystyle \alpha^{-1}=\alpha -1\) és hasonlóan \(\displaystyle \qquad \beta^{-1}=\beta -1.\) | (6) |
Ezt alkalmazva az (5) azonosság jobb oldalára, kapjuk, hogy \[\displaystyle \alpha^k (1+\alpha -1)+\beta^k (1+\beta -1)=\alpha^{k+1}+\beta^{k+1}.\] Így az állítást bebizonyítottuk. □
A következőkben megvizsgálunk két, az utolsó fejezetben felhasznált összefüggést a Fibonacci-számok és a Lucas-számok kapcsolatára, amelyek bebizonyítására alkalmazzuk a (4) Binet-formulát.
3.3. Lemma. Minden \(n \ge 1\) esetén teljesül, hogy
| \(\displaystyle L_n=F_n+2 F_{n-1}.\) | (7) |
Bizonyítás. Az állítás jobb oldalát felírjuk a (4) Binet-formula segítségével:
| \(\displaystyle \frac{1}{\sqrt{5}} (\alpha^n- \beta^n)+2 \frac{1}{\sqrt{5}} (\alpha^{n-1}- \beta^{n-1})=\frac{1}{\sqrt{5}} (\alpha^n+2 \alpha^{n-1})- \frac{1}{\sqrt{5}} (\beta^n+2 \beta^{n-1}).\) | (8) |
Alkalmazva (6)-ot a (8) jobb oldalára, kapjuk, hogy \[\displaystyle \frac{1}{\sqrt{5}}\alpha^n(2\alpha-1)-\frac{1}{\sqrt{5}}\beta^n(2\beta-1).\] Mivel \(2 \alpha-1=\sqrt{5}\) és \(2 \beta -1=-\sqrt{5}\), ezért a jobb oldal egyenlő \(\alpha^n+\beta^n\)-nel, ami a 3.2. Lemma szerint bizonyítja az állítást. □
3.4. Lemma. Minden \(n \ge 2\) esetén teljesül, hogy
| \(\displaystyle L_n=F_{n+2}-F_{n-2}.\) | (9) |
Bizonyítás. Az állítás jobb oldalát felírjuk a (4) Binet-formula segítségével:
| \[\displaystyle\begin{align}\frac{1}{\sqrt{5}}(\alpha^{n+2}-\beta^{n+2})-\frac{1}{\sqrt{5}}(\alpha^{n-2}-\beta^{n-2})&=\frac{1}{\sqrt{5}}(\alpha^{n+2}-\alpha^{n-2})-\frac{1}{\sqrt{5}}(\beta^{n+2}-\beta^{n-2})=\\ &=\frac{1}{\sqrt{5}}\alpha^n(\alpha^2-\alpha^{-2})-\frac{1}{\sqrt{5}}\beta^n(\beta^2-\beta^{-2}).\end{align}\] | (10) |
A (6) felhasználásával kapjuk, hogy \(\alpha^2-\alpha^{-2}=(\alpha+\alpha^{-1})(\alpha-\alpha^{-1})=(2 \alpha -1)=\sqrt{5}\) és \(\beta^2- \beta^{-2}=(\beta+\beta^{-1})(\beta-\beta^{-1})=(2 \beta -1)=-\sqrt{5}\). Így (10)-re azt nyerjük, hogy \(\alpha^n+\beta^n\), ami a 3.2. Lemmát felhasználva éppen \(L_n\). Ez bizonyítja az állítást. □
4. Egy geometriai kapcsolat a Fibonacci-sorozat és a Lucas-számok sorozata között
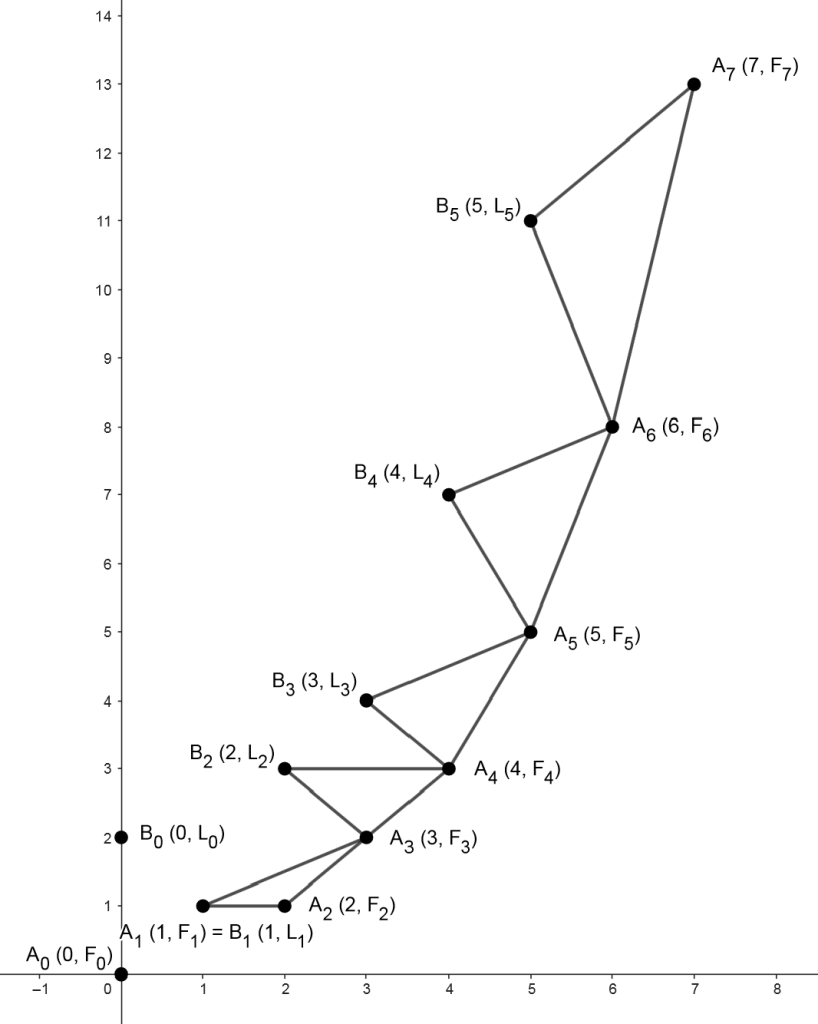
Érdekes geometriai kapcsolat fedezhető fel a 2. ábrán a Fibonacci- és a Lucas-számok felhasználásával létrehozott háromszögek sorozata között. Ha a derékszögű koordináta-rendszerben kijelöljük azokat a pontokat, amelyeknek \(x\) koordinátája \(0, 1, 2, 3, 4, 5, \dots,\) \(y\) koordinátája pedig a megfelelő indexű Fibonacci-, illetve Lucas-szám, akkor a pontokat az ábrán látható módon összekötve háromszögeket kapunk: A 2. ábrán jelölje \(B_{n}\) az \((n,L_n)\), illetve \(A_{n}\) az \((n,F_n)\) koordinátájú pontokat. Tekintsük azokat a háromszögeket, amelyek csúcspontjai \(B_{n-1}\), \(A_n\), és \(A_{n+1}\).

Jelölje rendre \(\bar{a}\), \(\bar{b}\) és \(\bar{c}\) a \(\overline{B_{n-1} A_{n+1}}\), \(\overline{B_{n-1} A_n}\), \(\overline{A_n A_{n+1}}\) vektorokat (lásd 3. ábra). Legyen \(n \ge 3\). A (9) összefüggést felhasználva kapjuk, hogy \[\displaystyle\begin{align}\bar{a}=\overline{B_{n-1} A_{n+1}}&=(n+1, F_{n+1})-(n-1, L_{n-1})=(2, F_{n+1}-L_{n-1})=\\ &=(2, F_{n+1}-F_{n+1}+F_{n-3})=(2,F_{n-3}).\end{align}\]
Az (1) és a (7) összefüggéseket alkalmazva \[\displaystyle\begin{align} \bar{b}=\overline{B_{n-1} A_n}&=(n, F_n)-(n-1, L_{n-1})=(1, F_n-L_{n-1})=(1,F_n-F_{n-1}-2F_{n-2})=\\ &=(1,F_n-F_{n-1}-2 F_n+2 F_{n-1})=(1,-F_n+F_{n-1})=(1,-F_{n-2}).\end{align}\] Alkalmazva az (1) összefüggést azt kapjuk, hogy \[\displaystyle \bar{c}=\overline{A_n A_{n+1}}=(n+1, F_{n+1})-(n, F_n)=(1, F_{n+1}-F_n)=(1, F_{n-1}).\]
A \(B_{n-1} A_n A_{n+1}\) háromszög \(B_{n-1}\) csúcsánál levő \(\theta_n\) szögének koszinuszára a koszinusztétel és az (1) segítségével azt kapjuk, hogy \[\displaystyle \cos\theta_n=\cos(B_{n-1}A_nA_{n+1}\sphericalangle)=\frac{|\bar{b}|^2+|\bar{a}|^2-|\bar{c}|^2}{2\cdot|\bar{a}|\cdot|\bar{b}|}=\frac{2-F_{n-3}\cdot F_{n-2}}{\sqrt{4+F_{n-3}^2}\sqrt{1+F_{n-2}^2}}.\]
A \(B_{n-1} A_n A_{n+1}\) háromszögek, ahol \(n \ge 3\), a következő állításokat elégítik ki ([7]).
4.1. Tétel. (i) A \(B_{n-1}\) csúcsnál lévő \(\theta_n\) szögek határértéke \[\displaystyle \lim_{n\to\infty}\theta_n=\pi.\]
(ii) A \(B_{n-1} A_n A_{n+1}\) háromszögek oldalhosszainak hányadosai a következő határértékekhez tartanak: \[\displaystyle \lim_{n\to\infty}\frac{|\overline{A_{n}A_{n+1}}|}{|\overline{B_{n-1}A_{n+1}}|}=\alpha^2,\qquad \lim_{n\to\infty} \frac{|\overline{B_{n-1}A_{n}}|}{|\overline{B_{n-1}A_{n+1}}|}=\lim_{n\to\infty} \frac{|\overline{A_{n}A_{n+1}}|}{|\overline{B_{n-1}A_{n}}|}=\alpha.\]
Bizonyítás. Meghatározzuk a \(\lim\limits_{n\to\infty}\cos (\theta_n)\) határértéket: \[\displaystyle \lim_{n\to\infty}\cos (\theta_n)=\lim_{n\to\infty}\frac{2-F_{n-3}\cdot F_{n-2}}{\sqrt{4+F_{n-3}^2}\sqrt{1+F_{n-2}^2}}=\lim_{n\to\infty}\frac{\frac{2}{F_{n-3} \cdot F_{n-2}}-1}{\sqrt{\frac{4}{F_{n-3}^2}+1} \sqrt{\frac{1}{F_{n-2}^2}+1}}=-1.\] Mivel a \([0, \pi]\) intervallumon \(\cos (\pi)=-1\), ezért \(\lim\limits_{n\to\infty}\theta_n=\pi\). Ez bizonyítja az (i) állítást.
Most kiszámítjuk a \(\lim\limits_{n\to\infty}\frac{\vert\overline{A_{n}A_{n+1}}\vert}{\vert\overline{B_{n-1}A_{n+1}}\vert}\) határértéket: \[\displaystyle \lim_{n\to\infty}\frac{\overline{|A_n A_{n+1}|}}{\overline{|B_{n-1} A_{n+1}|}}=\lim_{n\to\infty}\frac{\sqrt{1+F_{n-1}^2}}{\sqrt{4+F_{n-3}^2}}=\lim_{n\to\infty}\sqrt{\frac{\frac{1}{F_{n-3}^2}+\frac{F_{n-1}^2}{F_{n-3}^2}}{\frac{4}{F_{n-3}^2}+\frac{F_{n-3}^2}{F_{n-3}^2}}}=\lim_{n\to\infty}\frac{F_{n-1}}{F_{n-3}}.\] Felhasználva a (4) Binet-formulát és azt, hogy \(\left\vert\frac{\beta}{\alpha}\right\vert<1\) azt kapjuk, hogy \[\displaystyle\begin{align} \lim_{n\to\infty}\dfrac{F_{n-1}}{F_{n-3}}&=\lim_{n\to\infty}\dfrac{\frac{\alpha^{n-1}-\beta^{n-1}}{\sqrt{5}}}{\frac{\alpha^{n-3}-\beta^{n-3}}{\sqrt{5}}}=\lim_{n\to\infty}\dfrac{\alpha^{n-1}-\beta^{n-1}}{\alpha^{n-3}-\beta^{n-3}}=\\ &=\lim_{n\to\infty}\dfrac{\frac{\alpha^{n-1}}{\alpha^{n-3}}-\frac{\beta^{n-1}}{\alpha^{n-3}}}{\frac{\alpha^{n-3}}{\alpha^{n-3}}-\frac{\beta^{n-3}}{\alpha^{n-3}}}=\lim_{n\to\infty}\dfrac{\alpha^2-\beta^2\left(\frac{\beta}{\alpha}\right)^{n-3}}{1-\left(\frac{\beta}{\alpha}\right)^{n-3}}=\alpha^2.\end{align}\]
Tehát az állítás (ii) részében szereplő első határérték valóban \(\alpha^2\).
Hasonlóan kapjuk, hogy \[\displaystyle\begin{align} \lim_{n\to\infty}\dfrac{\overline{|B_{n-1} A_{n}|}}{\overline{|B_{n-1}A_{n+1}|}}&=\lim_{n\to\infty}\dfrac{\sqrt{1+F_{n-2}^2}}{\sqrt{4+F_{n-3}^2}}=\lim_{n\to\infty}\sqrt{\dfrac{\frac{1}{F_{n-3}^2}+\frac{F_{n-2}^2}{F_{n-3}^2}}{\frac{4}{F_{n-3}^2}+\frac{F_{n-3}^2}{F_{n-3}^2}}}=\lim_{n\to\infty}\dfrac{F_{n-2}}{F_{n-3}}=\\ =\lim_{n\to\infty}\dfrac{\frac{\alpha^{n-2}-\beta^{n-2}}{\sqrt{5}}}{\frac{\alpha^{n-3}-\beta^{n-3}}{\sqrt{5}}}&=\lim_{n\to\infty}\dfrac{\alpha^{n-2}-\beta^{n-2}}{\alpha^{n-3}-\beta^{n-3}}=\lim_{n\to\infty}\dfrac{\frac{\alpha^{n-2}}{\alpha^{n-3}}-\frac{\beta^{n-2}}{\alpha^{n-3}}}{\frac{\alpha^{n-3}}{\alpha^{n-3}}- \frac{\beta^{n-3}}{\alpha^{n-3}}}=\\ &=\lim_{n\to\infty}\frac{\alpha-\beta \left(\frac{\beta}{\alpha}\right)^{n-3}}{1-\left(\frac{\beta}{\alpha}\right)^{n-3}}=\alpha.\end{align}\]
Tehát az állítás (ii) részében szereplő második határértéket is kiszámítottuk.
Végezetül meghatározzuk az (ii) rész harmadik, \(\lim\limits_{n\to\infty}\frac{\vert\overline{A_{n}A_{n+1}}\vert}{\vert\overline{B_{n-1}A_{n}}\vert}\) határértékét: \[\displaystyle \begin{align} \lim_{n\to\infty}\dfrac{|\overline{A_{n}A_{n+1}}|}{|\overline{B_{n-1}A_{n}}|}&=\lim_{n\to\infty} \dfrac{\sqrt{1+F_{n-1}^2}}{\sqrt{1+F_{n-2}^2}}=\lim_{n\to\infty} \sqrt{\dfrac{\frac{1}{F_{n-2}^2}+\frac{F_{n-1}^2}{F_{n-2}^2}}{\frac{1}{F_{n-2}^2}+\frac{F_{n-2}^2}{F_{n-2}^2}}}=\lim_{n\to\infty} \dfrac{F_{n-1}}{F_{n-2}}=\\ &=\lim_{n\to\infty}\dfrac{\frac{\alpha^{n-1}-\beta^{n-1}}{\sqrt{5}}}{\frac{\alpha^{n-2}-\beta^{n-2}}{\sqrt{5}}}=\lim_{n\to\infty} \dfrac{\alpha^{n-1}-\beta^{n-1}}{\alpha^{n-2}-\beta^{n-2}}=\lim_{n\to\infty} \dfrac{\frac{\alpha^{n-1}}{\alpha^{n-2}}-\frac{\beta^{n-1}}{\alpha^{n-2}}}{\frac{\alpha^{n-2}}{\alpha^{n-2}}-\frac{\beta^{n-2}}{\alpha^{n-2}}}=\\ &=\lim_{n\to\infty}\dfrac{\alpha-\beta\left(\frac{\beta}{\alpha}\right)^{n-2}}{1-\left(\frac{\beta}{\alpha}\right)^{n-2}}=\alpha.\end{align}\] Így a tétel állítását bebizonyítottuk. □
Irodalomjegyzék
[1] B. Barik, Lucas sequence, its properties and generalization. MSc Thesis, National Institute of Technology Rourkela (2013), http://ethesis.nitrkl.ac.in/5270/1/411MA2130.pdf.
[2] Bees and Fibonacci Sequence, Beekeeping and aquaculture, Module 6, Livestock, Unit 18, New Agriways, EDISCO Editrice, 1-3,
https://www.edisco.it/newagriways/wpcontent/uploads/
[3] B. Énekes, G. Kós, Néhány érdekesség a Fibonacci- és a Fibonacci-típusú sorozatokról, KöMaL, 2000/december, 517–523, http://db.komal.hu/KomalHU/cikk.phtml?id=200117.
[4] A. Grigas, The Fibonacci Sequence: Its History, Significance, and Manifestations in Nature, Senior Honors Theses. 334 (2013), https://digitalcommons.liberty.edu/honors/334.
[5] T. Gross, A secret of bees, https://www.bristol.ac.uk/media-library/sites/engineering/engineering-mathematics/documents/modelling/teacher/bees_t.pdf
[6] R. Herz-Fischler, Letter to the Editor, Fibonacci Quart. 24 (4) (1986) 382.
[7] I. M. Radu, A geometric approach to Fibonacci and Lucas sequences. Parabola, 56 (1) (2020) 1–5.
Munkánkat a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal (NKFI) K132951 támogatta.
Figula Ágota
Debreceni Egyetem, TTK, Matematikai Intézet
Silling Szintia Adriána
Debreceni Egyetem, GTK, Turizmus-vendéglátás szakos BSc hallgató