A 2024-es MEMO néhány feladatának részletes megoldása

A csapat beszámolója a versenyről itt olvasható: 1. rész, 2. rész.

A teljes feladatsor és az angol nyelvű megoldások a MEMO hivatalos honlapján érhetők el.

I-1. feladat

Határozd meg az összes olyan \(k\in \mathbb{N}_0\) számot, amelyre létezik olyan \(f\colon \mathbb{N}_0\rightarrow\mathbb{N}_0\) függvény, hogy \(f(2024)=k\) és \[\displaystyle f(f(n))\leq f(n+1)-f(n)\] teljesül minden \(n\in\mathbb{N}_0\) számra.

Megjegyzés. A feladatban \(\mathbb{N}_0\) a nemnegatív egész számok halmazát jelöli.

Prohászka Bulcsú megoldása

A válasz az, hogy pontosan azok a \(k\)-k teljesítik a feltételt, amelyekre \(0\leq k\leq 2023\). Ezekre gyorsan mutatunk is egy megfelelő függvényt: \(f(n)\) legyen 0, ha \(n\leq k\), és legyen \(k\), ha \(n>k\). Vegyük észre, hogy ebben az esetben \(f(f(n))=0\) minden \(n\)-re, hisz \(f(n)\leq k\), továbbá, hogy ez a függvény (kicsit furcsán, de) monoton nő, vagyis \(f(n)\leq f(n+1)\) minden \(n\)-re. Viszont így tudjuk, hogy \(f(f(n))=0\leq f(n+1)-f(n)\), vagyis a függvényünk tényleg teljesíti a feltételt.

Lássuk, hogy miért nem teljesülhet \(f(2024)\geq2024\). Azt az erősebb állítást fogjuk belátni, hogy semmilyen \(n\geq 2\) egészre nem lehet \(f(n)\geq n\).

Az első fontos észrevétel, hogy \(f\) monoton nő, hiszen bármely \(n\)-re \(f(n+1)-f(n)=f(f(n))\geq0\), vagyis tényleg \(f(n)\leq f(n+1)\).

Először csak azt látjuk be, hogy semmilyen \(n\in\mathbb{N}_0\)-ra nem teljesülhet \(f(n)>n\). Legyen az indirekt feltevés az, hogy mégis van egy olyan \(n\) szám, amelyre \(f(n)>n\), vagyis \(f(n)\geq n+1\). Ebből a monotonitás miatt következik, hogy \(f(f(n))\geq f(n+1)\), vagyis \(0\geq f(n+1)-f(f(n))\). Viszont ekkor az alapfeltételt átrendezve kapjuk, hogy \[\displaystyle n<f(n)=f(n+1)-f(f(n))\leq 0,\] ami \(n>0\)-ra ellentmondás.

Most már tudjuk, hogy \(f(n)\leq n\), már csak azt kell belátnunk, hogy ha \(n>1\), akkor \(f(n)\neq n\). Indirekt módon tegyük fel, hogy \(f(n)=n\) valamely egynél nagyobb \(n\) egész számra. Természetesen most is a feltételt fogjuk kihasználni: ha \(f(n)=n\), akkor \[\displaystyle n=f(n)=f(f(n))\leq f(n+1)-f(n) = f(n+1)-n.\] Ezt átrendezve kapjuk, hogy \(2n\leq f(n+1)\). Ez viszont ellentmondás, hiszen azt már tudjuk, hogy \(f(n+1)\leq n+1\), tehát \(2n\leq n+1\)-ből \(n\leq1\) következne. Ezzel készen lettünk.

I-4. feladat

Egy \(n\) pozitív egészre \(\sigma(n)\) jelölje \(n\) pozitív osztóinak összegét. Határozd meg az összes egész együtthatós \(P\) polinomot, amelyre \(P(k)\) osztható \(\sigma(k)\)-val minden \(k\) pozitív egészre.

Keresztély Zsófia megoldása

A válasz az, hogy az egyedüli ilyen polinom a nullpolinom, vagyis \(P(x) \equiv 0\). A bizonyítás során jelölje \(v_p(b)\) a \(b\) egész szám prímtényezős felbontásában a \(p\) prím kitevőjét. Először belátunk egy lemmát.

Lemma: Tetszőleges \(n\geq 0\)-ra létezik \(m>0\), amelyre \(3^m\equiv1 \pmod{2^n}\).

Bizonyítás: Ez az Euler–Fermat-tétel egyenes következménye, hiszen 3 és \(2^n\) relatív prímek, vagyis \(3^{\varphi\left(2^n\right)}\equiv 1 \pmod{2^n}\). □

Legyen \(P(x) = \sum_{i=0}^n a_ix^i\). Indirekt módon tegyük fel, hogy létezik olyan \(a_i\) érték, amely nemnulla, legyen a legkisebb ilyen \(i\) az \(L\).

A lemma alapján tudjuk, hogy tetszőleges \(N\) természetes szám esetén létezik olyan \(M\), amelyre \(2^{N(L+1)+1} \mid 3^M-1\), vagyis \(2^{N(L+1)} \mid \frac{3^M-1}{2}\). Ekkor legyen \(K = 2^N \cdot 3^{M-1}\), amelyre a híres osztóösszegképlet ( \(n = \prod_{i=1}^k p_i^{\alpha_i}\) esetén \(\sigma (n) = \prod_{i=1}^k \frac{p_i^{\alpha_i+1}-1}{p_i-1}\)) alapján tudjuk, hogy \(\sigma (K) = \left( 2^{N+1}-1 \right) \cdot \frac{3^M-1}{2}\). Vagyis tudjuk, hogy \[\displaystyle 2^{N(L+1)} \mid \frac12(3^M-1) \mid \sigma (K) \mid P(K).\]

Tekintsük \(P(K)\) monomjait. Mivel minden \(i<L\)-re \(a_i = 0\), így \(2^{N(L+1)} \mid a_iK^i\) teljesül minden \(i<L\)-re. Továbbá minden \(i>L\)-re \(2^{N(L+1)} \mid \left(2^{N}\right)^i \mid K^i \mid a_iK^i\) (itt használjuk, hogy a polinom egész együtthatós). Mivel \(2^{N(L+1)} \mid P(K)\), és beláttuk, hogy \(2^{N(L+1)}\) osztja \(P(K)\) minden \(a_LK^L\)-en kívüli monomját, így \(2^{N(L+1)} \mid a_LK^L\). Vagyis \(N(L+1) \leq v_2(a_LK^L) = v_2(a_L) + NL\), tehát \(N \leq v_2(a_L)\), vagyis \(2^N \mid a_L\). Azonban \(N\) tetszőleges természetes szám lehet, ami azt jelenti, hogy \(a_L\)-nek van tetszőlegesen nagy pozitív osztója. Ebből következik, hogy \(a_L\) csak 0 lehet, ami ellentmondáshoz vezet, hiszen \(a_L\) a legkisebb indexű nemnulla együttható.

Tehát az indirekt feltevésünk hamis volt, vagyis minden \(a_i\) együtthatója 0 a \(P\) polinomnak, vagyis \(P\) valóban csak a nullpolinom lehet.

T-3. feladat

A Tisza partján 2024 matematikus ül egy sorban. Mindegyikük pontosan egy kutatási témán dolgozik, és ha két matematikus azonos témán dolgozik, akkor az összes közöttük ülő matematikus is ugyanezen a témán dolgozik.

Marvin az összes, két matematikusból álló párra ki szeretné deríteni, hogy azonos témán dolgoznak-e vagy sem. Ehhez bármely matematikustól megkérdezheti az alábbi kérdést: „A 2024 matematikus közül hányan dolgoznak a témádon?” A kérdéseket egyesével teszi fel, így mielőtt feltesz egy kérdést, már tudja az összes előzőre kapott választ.

Határozzátok meg a legkisebb \(k\) pozitív egészt, amelyre Marvin mindenképpen teljesíteni tudja a célját legfeljebb \(k\) kérdéssel.

Molnár István Ádám megoldása

Először megmutatjuk, hogy 2023 kérdéssel teljesíteni tudja a feladatot. Kérdezze meg az első 2023 matematikust. Az első matematikus válaszából tudni fogja, hogy az első hány matematikus dolgozik ugyanazon a témán. Őket figyelmen kívül hagyva (hiszen más már nem dolgozhat ugyanazon a kutatási témán), megkérdezi az újonnan első matematikust és ezt a folyamatot folytatja. Az utolsó matematikust nem kell megkérdeznie, hiszen, ha már csak ő maradt, akkor ő az egyetlen, aki azon a kutatási témán dolgozik.

A matematikusok viszont meg tudják oldani, hogy Marvinnak legalább 2023-szor kelljen kérdeznie a következő csalfa stratégiával. Hívjuk partnak a már válaszolt matematikusok egybefüggő részhalmazát, amelynek az egyik széle után nincs matematikus, másik széle után egy olyan matematikus van, aki még nem válaszolt. A szigetet definiáljuk hasonlóan, de ennek mindkét széle után egy még nem válaszolt matematikus legyen. Példa:

Válaszok számként, ismeretlenek kérdőjellel. Balról jobbra: egy part (piros), két sziget (sárga, zöld) és egy part (kék).

Hívjuk csoportnak az azonos témán dolgozó matematikusok halmazát. A matematikusok célja, hogy a parthatár csoporthatár legyen, továbbá a szigetek csak 2-esekből álljanak. (Intuitívan a parti válaszok ne adjanak információt a nem parti részekről.)

\(\bullet\) Ha a válasz egy szigetet hozna létre, szigetet bővítene vagy két szigetet csatolna össze, a matematikusok 2-vel válaszolnak.

\(\bullet\) Ha a válasz partot bővítene vagy hozna létre, a matematikusok 1-gyel válaszolnak, így a part ezen egyes csoporttal végződik.

\(\bullet\) Ha a válasz a parthoz egy szigetet kötne, akkor a matematikusok 1-essel válaszolnak, ha a sziget páros sok 2-esből áll, és 2-essel különben. Így a parthoz hozzácsatolt válaszokban egy csoport vagy teljesen benne van, vagy egyáltalán nincs benne.

Ha Marvin legfeljebb 2022 kérdést tenne fel, akkor kell lennie legalább két matematikusnak, aki még nem válaszolt.

\(\bullet\) Ha a nem válaszolt matematikusok összefüggőek, akkor nincs sziget. Nem tudhatjuk, hogy minden nem válaszolt matematikus ugyanazon témán dolgozik-e vagy különbözőn (és mivel legalább két matematikus van, ezen esetek különbözők), hiszen a partok erről nem árulnak el információt.

\(\bullet\) Különben tekintsük az első és az utolsó matematikust, aki nem válaszolt. Ha az ő általuk meghatározott zárt intervallumban páros sok matematikus van, akkor nem tudjuk megkülönböztetni az eseteket, ahol a csoportok méretek rendre 2, 2, 2, …, 2, 2, illetve 1, 2, 2, …, 2, 1; ha páratlan, akkor az 1, 2, 2, …, 2, 2, és 2, 2, 2, …, 2, 1 eseteket. Ezen két matematikus között csak szigetek lehetnek, ahol minden matematikus 2-vel válaszolt, így ezen esetek lehetségesek.

Ezzel tehát beláttuk, hogy 2023 kérdés biztosan elég Marvinnak, de 2022 kérdés nem elég biztosan.

T-5. feladat

Legyen \(ABC\) egy olyan háromszög, amelyben \(BAC\sphericalangle = 60^{\circ}\). Legyen \(D\) az \(AC\) egyenes egy pontja, amelyre \(AB = AD\) és az \(A\) pont \(C\) és \(D\) között fekszik. Tegyük fel, hogy \(E \neq F\) két olyan pont a \(DBC\) háromszög köréírt körén, amelyekre \(AE = AF = BC\). Bizonyítsátok be, hogy az \(EF\) egyenes áthalad az \(ABC\) háromszög köréírt körének középpontján.

Kovács Benedek Noel megoldása

Készítsünk ábrát, és használjuk az alábbi jelölésrendszert!

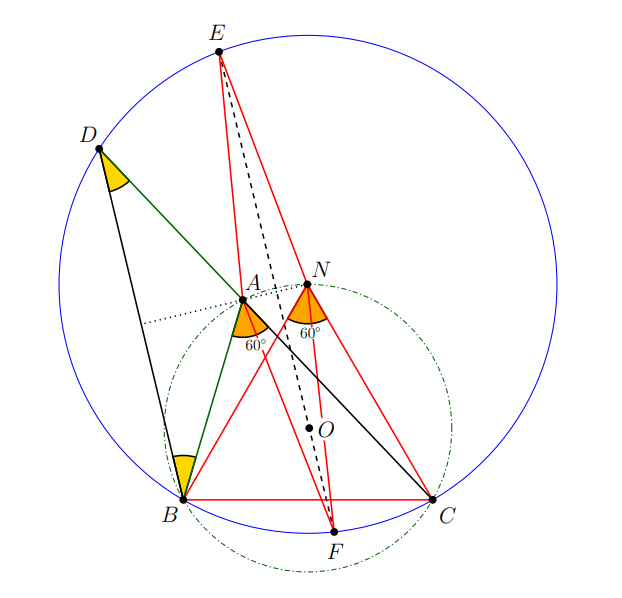
Mivel \(DAB\sphericalangle=180^{\circ}-BAC\sphericalangle=120^{\circ}\), így az \(ABD\) egyenlő szárú háromszögben \(ABD\sphericalangle=ADB\sphericalangle=\frac{180^{\circ}-DAB\sphericalangle}{2}=30^{\circ}\) lesz. A középponti és kerületi szögek tételéből következik, hogy a \(BCD\) háromszög köréírt körének \(N\) középpontjára \(BNC\sphericalangle=2\cdot BDC\sphericalangle=60^{\circ}\) teljesül.

Innen látható, hogy mivel \(BNC\sphericalangle=BAC\sphericalangle=60^{\circ}\), így a kerületi szögek tételének megfordításából következik, hogy \(N\) az \(ABC\) háromszög körülírt körén helyezkedik el.

Azt is tudjuk, hogy mivel \(BN=CN\), így \(NBC\sphericalangle=NCB\sphericalangle=\frac{180^{\circ}-BNC\sphericalangle}{2}=60^{\circ}\) lesz, azaz az \(NBC\) háromszög szabályos, amelynek eredményeképpen \(BC=BN=CN\) lesz.

Mivel \(E\) és \(F\) pontok is rajta vannak az \(N\) középpontú körön (\(BCD\) háromszög köréírt körén), így \(EN=NF=BC\) lesz. Ezen kívül a feladat szövege alapján \(AE = AF = BC\). Ebből az következik, hogy \(AE=AF=EN=EF\), tehát \(AENF\) egy rombusz lesz. Ennek alapján látható, hogy az \(EF\) egyenes az \(AN\) szakasz felezőmerőlegese lesz.

Azonban ismert, ahogy az \(A\) és \(N\) pontok egyaránt rajta vannak az \(ABC\) háromszög \(O\) középpontú köréírt körén, úgy az \(O\) pont rajta lesz az \(AN\) szakasz felezőmerőlegesén.

Mindezekből az következik, hogy az \(E\), \(F\), \(O\) pontok kollineárisak lesznek, vagyis az \(EF\) egyenes valóban áthalad az \(ABC\) háromszög köréírt körének \(O\) középpontján.

T-6. feladat

Legyen \(ABC\) egy hegyesszögű háromszög. Legyen a \(BC\) szakasz felezőpontja \(M\). Legyen \(I\), \(J\), \(K\) rendre az \(ABC\), \(ABM\), \(ACM\) háromszögek beírt körének középpontja. Legyenek \(P\), \(Q\) rendre az \(MK\), \(MJ\) egyeneseken olyan pontok, hogy \(AJP\sphericalangle=ABC\sphericalangle\) és \(AKQ\sphericalangle =BCA\sphericalangle\). Legyen a \(CP\) és \(BQ\) egyenesek metszéspontja \(R\). Bizonyítsátok be, hogy az \(IR\) és \(BC\) egyenesek merőlegesek egymásra.

Vigh Zalán megoldása

Ha megmutatjuk, hogy \(BI \perp CP\), akkor hasonlóan \(CI \perp BQ\), így azt kapjuk, hogy \(I\) a \(BCR\triangle\) magasságpontja, így \(RI \perp BC\). Tehát a célunk, hogy belássuk,  \(BI \perp CP\).

\(I\), \(J\) és \(K\) mindegyike \(A\)-ból, \(C\)-ből, \(B\)-ből és \(M\)-ből induló szögfelezők metszete, így kapjuk, hogy \(MJ \perp MK\). Megnézve az \(AJM\) háromszög belső szögeit, kapjuk, hogy \(AJM\sphericalangle = 90^\circ + \frac{ABC\sphericalangle}{2}\). Mivel \(AJP\sphericalangle=ABC\sphericalangle\), így \(PJM\sphericalangle = 90^\circ – \frac{ABC\sphericalangle}{2}\). Továbbá megnézve a \(JMP\) háromszög szögeit, kapjuk, hogy \(JPM\sphericalangle = \frac{ABC\sphericalangle}{2}\).

Legyen \(J’\) a \(J\) pont tükörképe \(M\)-re!

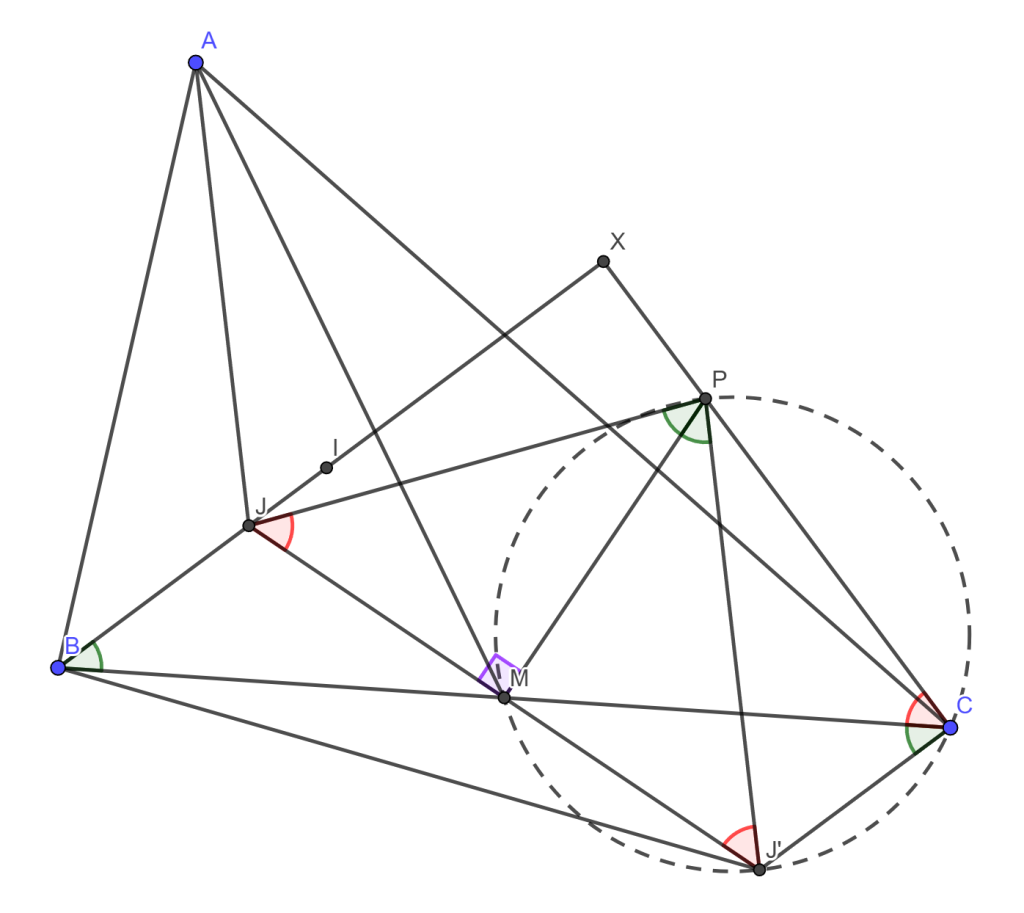
Ekkor a tükrözés miatt \(BJC\triangle \cong CJ’B\triangle\), valamint \(JMP\triangle \cong J’MP\triangle\), így azt kapjuk, hogy \(J’CM\sphericalangle = JBM\sphericalangle = \frac{ABC\sphericalangle}{2} = JPM\sphericalangle = J’PM\sphericalangle\).

Így \(P\) és \(C\) ugyanakkora szögben lát rá a \(J’M\) szakaszra, tehát \(J’MPC\) egy húrnégyszög. A kerületi szögek tétele alapján \(MCP\sphericalangle = MJ’P\sphericalangle = MJP\sphericalangle = 90^\circ – \frac{ABC\sphericalangle}{2}\). Legyen \(BI\) metszete \(CP\)-vel \(X\). Ekkor megnézve \(BXC\triangle\) szögeit, kapjuk, hogy \(BXC\sphericalangle = 90^\circ\), tehát \(BI \perp CP\).

T-7. feladat

Nevezzük pozitív egészek összeragasztásának a tízes számrendszerbeli alakjuk egymás után írását, majd a kapott eredmény leolvasását egyetlen, tízes számrendszerben írt pozitív egészként.

Adjátok meg az összes olyan pozitív egész \(k\) számot, amelyre létezik \(N_k\) egész az alábbi tulajdonsággal: minden \(n\geq N_k\)-ra az 1, 2, …, \(n\) számok összeragaszthatók valamilyen sorrendben úgy, hogy az eredmény osztható legyen \(k\)-val.

Megjegyzés. A tízes számrendszerbeli alakja egy pozitív egésznek sosem kezdődik 0-val.

Példa. A 15, 14, 7 számok ilyen sorrendbeli összeragasztása 15147.

Holló Martin megoldása

Megmutatjuk, hogy pontosan a 3-mal nem osztható számok rendelkeznek ezzel a tulajdonsággal.

Először megmutatjuk, hogy a 3-mal osztható \(k\)-k nem rendelkeznek ezzel a tulajdonsággal, ehhez elég megmutatni, hogy a 3 nem rendelkezik ezzel a tulajdonsággal. Hiszen \(k=3\) esetén az oszthatóság csak a számok számjegyeinek összegétől függ, de minden \(N_3\) szám esetén van nála nagyobb \(n\), ami 10-hatvány, ami 1-gyel változtatja az addigi számok számjegyösszegét. Így akkor az oszthatóság biztosan megváltozik, tehát vagy addig nem teljesült, vagy mostantól nem fog. Így ezt beláttuk.

Most megmutatjuk, hogy a 3-mal nem osztható számokra teljesül az állítás.

Ekkor \(k\)-t írjuk fel \(k’\cdot 2^m\cdot 5^{\ell}\) alakban, ahol \(k’\) egész és nem osztható sem 2-vel, sem 5-tel. Világos, hogy ezt mindig megtehetjük.

Az lesz a stratégia, hogy egy bizonyos \(N_k\) szám esetén elérjük, hogy az első \(N_k\) számot össze tudjuk ragasztani tetszőleges \(k’\)-vel vett maradékot adó számmá úgy, hogy az utolsónak ragasztott szám egy olyan nagy 10-hatvány legyen, ami többszöröse \(2^m\cdot 5^{\ell}\)-nek.

Belátjuk, hogy ez a stratégia valóban működik. Vegyük az \(N_k\)-nál nagyobb számok egy tetszőleges összeragasztását, és írjunk a szám végére annyi 0-t, amennyi számjegyből az első \(N_k\) szám összesen áll. Nézzük meg az így kapott szám maradékát \(k’\)-vel osztva. Ekkor ha a szám után odaragasztjuk azt az első \(N_k\) számból álló számot, ahol a maradék ennek az ellentettje, akkor egy \(k’\)-vel osztható számot kapunk, ami a nagy 10-hatvánnyal való végződés miatt \(2^m\cdot 5^{\ell}\)-lel is osztható lesz. Így a relatív prímség miatt a szám osztható lesz \(k\)-val is.

Most térjünk rá a konstrukcióra: először kezdjük azzal, hogy az elég nagy 10-hatványt a szám végére rakjuk. Ezek után úgy fogjuk elé ragasztani a számokat, hogy az tartalmazzon \(k’\) db különböző párt, ahol a pár két olyan egymás mellé ragasztott \(A\) és \(B\) számot jelöl, amelyekre \(A\) és \(B\) felcserélése 1-gyel növeli a szám \(k’\)-vel való maradékát. Ekkor \(k’\) ilyen pár esetén összesen \(k’\) helyen tudjuk egyesével növelni a maradékot, így tetszőleges értéket elérve. Most kezdjük el a szám végétől indulva egyesével létrehozni ezeket a párokat.

Induktívan tegyük fel, hogy már létrehoztunk valamennyi ilyen párt; most megmutatjuk, hogy tudunk csinálni még egyet. Ha eddig \(i\) számjegyből áll a szám, akkor ha \(N_k\) elég nagy, akkor biztos van még nem felhasznált számunk úgy, hogy annak a számnak a számjegyeinek száma tetszőleges maradékot adjon \(\varphi(k’)\)-vel osztva. Ezt megfelelően választva elérhető, hogy a szám elé írva a jelenlegi szám számjegyeinek száma \(\varphi(k’)\)-vel osztható legyen. Így ezt a számot írjuk is a szám elé. Illetve ha \(N_k\) elég nagy, akkor biztos van még \(k’\) egymást követő fel nem használt szám, amelyek számjegyeinek száma mind azonos, és \(\varphi(k’)\)-vel osztva 1-et ad maradékul. Ekkor a \(k’\) szám közül legyen \(B\) az, amelyik osztható \(k’\)-vel, és legyen \(A\) az, aminek a \(k’\)-s maradéka a 9 inverze. (Ilyen \(A\) van, hisz a 9 és \(k’\) relatív prímek, ahogy \(k\) nem osztható 3-mal.)

Ekkor ha a jelenlegi szám elejére írjuk \(A\)-t, majd utána az elé \(B\)-t, akkor egy jó párt kapunk, hiszen ha \(A\)-nak \(j\) számjegye van, és utána még \(c\) számjegy van, akkor a két szám megcserélésével a maradék változása \[\displaystyle A\cdot 10^c\cdot 10^j+B\cdot 10^c-(A\cdot 10^c+B\cdot 10^c \cdot 10^j).\]

De mivel \(B\) osztható \(k’\)-vel, a \(B\)-s tagokat elhagyhatjuk, így a változás \[\displaystyle A\cdot 10^c\cdot (10^j-1).\]

De mivel \(c\) a \(\varphi(k’)\) többszöröse és a \(k’\) és 10 relatív prímek, így az Euler–Fermat-tétel miatt a \(10^c\) szám 1 maradékot ad \(k’\)-vel osztva, így azzal leoszthatunk, és a változás \(A\cdot (10^j-1)\) lesz. De mivel \(10^{j-1}\) maradéka 1 az Euler–Fermat-tétel miatt, így \(10^j\) maradéka 10, tehát \(10^j-1\) maradéka \(k’\)-vel osztva 9. Ekkor \(A\cdot (10^j-1)\) az 1-et ad maradékul, tehát csináltunk egy párt, aminek felcserélése 1-gyel növeli a maradékot. Ez az algoritmus folytatható a következő pár létrehozásánál is, amivel kész lettünk. A megmaradó számokat pedig a szám elejére ragasztjuk.

Hegedűs Dániel és Kovács Benedek,
MEMO csapatvezetők