Interjú Veres Dorottyával
Mikor találkoztál a matematikával?
Még óvodás koromban kezdtem el matekozni – a szüleim segítettek, mert látták, hogy ügyes vagyok benne.
Ez miből derült ki számukra?
Négyévesen a kedvenc könyvem egy szorzótáblás könyv volt. Édesapám fizikus, mesélt a π-ről, a gyökvonásról. Szerettem hallgatni, érdekelt, kérdezgettem. Otthon, iskola után is szívesen matekoztam, már akkor is találtam ki magamtól saját feladatokat.
Másodikig egy 17. kerületi általános iskolába jártam, de eljártam a Fazekasba matekszakkörre, ahová harmadiktól már át is vettek. Attól kezdve minden matekversenyre elmentem, amik jól is sikerültek. A felsőben tapasztaltam meg Pereczes Marianna tanárnő révén, hogy milyen a felfedeztető matematikatanítás. El is határoztam, hogy a matek szak elvégzése után kutató leszek, mert nagyon tetszett, hogy nem leadják nekem a tananyagot, hanem magamtól jöhetek rá, találhatom ki. Hatodikosként már biztos voltam benne, hogy matematikus leszek. Hetediktől átvettek a specmatra, ahol – ha lehet – még „matekosabb” lett a környezetem– innentől Hujter Bálint, Gyenes Zoltán és dr. Kiss Géza tanítottak.
A matematika felfedezésének örömét élhettem át a MaMuT, EGMO, illetve hétvégi Pósa-táborokban is. Ezekben az tetszik különösen, hogy nem versenycentrikusak, hanem érdekesek: olyan témák kerülnek elő, amelyek nem a tananyaghoz vagy a versenyekhez kapcsolódnak, hanem inkább kitekintő témakörök.
Annyira nem is szeretek versenyezni, nem célom, hogy kijussak például az EGMO-ra. Szeretem a matekot, de főleg a kutatás vonz.
Idén nyáron mégis voltál olimpián!
Igen. Részt vettem Tajvanon a 22. Nemzetközi Nyelvészeti Diákolimpián. A nyelvek, és főleg a logikájuk – azaz, hogy hogyan épülnek fel – mindig is érdekelt. A szüleimnek szoktam előadást tartani különböző témákban, például japán nyelvtanból. Édesanyám biztatott, hogy induljak el a válogatón, mert szerinte biztosan ügyes lennék belőle. Bekerültem a top60-ba, és onnantól már nagyon szerettem volna kijutni az olimpiára. Úgyhogy elkezdtem készülni rá rendesen. Sok motivációt kaptam magyartanáromtól, dr. Oláh Tibortól is. Végül másodikként kerültem be a csapatba, ott pedig dicséretet (honorable mention) kaptam. Az Ázsiai és Óceániai Nyelvész Olimpián is indulhattam itthonról, vendég résztvevőként bronzérmet kaptam.
Szerintem olyan a nyelvészet, mint a matek, csak szavakkal. Az is jó benne, hogy kisebb a nyomás: mivel nem ez a fő profilom, nem érzem, hogy itt feltétlenül teljesíteni kellene.
A nyelveket is szereted, vagy főleg a nyelvtan érdekel?
Inkább a nyelvtan. Írni sokféle ábécével tudok – a japánt már nagyon régen megtanultam, az iskolában az oroszt is. Németül is tanultam, angolul pedig jól beszélek, de ez ma már alap.
Még hogyan kapcsolódsz ki?
Sok különleges sportot kipróbáltam már: műugrás, légtorna, műkorcsolya. Sok évig táncoltam és úsztam is. Nincs a nyelvvel vagy a sportokkal célom, elsősorban a matek érdekel, a többi csak szórakozás.
Igazából úgy szeretek matekozni, hogy közben mást is csinálok: járkálok a szobában, ordít közben a zene. Valamiért kell, hogy az agyamat egyszerre más is lefoglalja a matek mellett. Nehéz számomra csendben, egyhelyben ülve gondolkodni. Például a matektáborokban is össze szoktam tolni pár asztalt, rájuk fekszem, és úgy jobban megy a feladatmegoldás.
Annyira megy a matekozás, hogy most júliusban az Acta Mathematica Hungarica folyóiratban publikációd is megjelent. A folyóirat 75 éves történetében először közölték egy középiskolás cikkét! Mesélj erről!
Már nagyon régóta magasan a geometria a kedvenc témaköröm: a táborokban, illetve magamtól is a projektív geometriával foglalkozom a legszívesebben. Az egyik EGMO-tábor témája a topológia volt, ami magával ragadott, úgyhogy utána kértem is további olvasnivalót. Aztán szerettem volna nyitott problémákon gondolkodni, lehetőleg a geometria és a topológia metszetén belül. Keresgéltem az interneten, és amikor a hiperbolikus geometriára rátaláltam, akkor rögtön éreztem, hogy ez jó lesz: semmit sem tudok róla, de nagyon érdekes.
Reiman István A geometria és határterületei, illetve Kálmán Attila Nemeuklideszi geometriák elemei című könyveit nézegettem, de a bonyolult számolásokat nem is értettem meg, illetve nem is tartottam szépnek. Mindenhol hosszú differenciálgeometriai számolások, vagy szögfüggvények voltak. Arra gondoltam, hogy ha én egyszer kutató matematikus leszek, akkor nehogy már csak számolgatnom kelljen. Ezért nem a távolságmérős részét próbáltam olvasni a szakirodalomnak, hanem a tiszta, elemi geometriásat.
Egyik este nem tudtam aludni, és egyszer csak eszembe jutott, hogy még korábban találtam a GeoGebrának egy olyan programját, ami mindent meg tudott nekem szerkeszteni. Például, ha egy körlapon – mint a Poincaré-féle modellben – kijelölök két pontot, akkor (nagyon jó közelítéssel) összeköti őket. Arra gondoltam, hogy ezt jó lenne a papírlapon, euklideszi eszközökkel is megszerkeszteni – a cikk elejére került be ennek a megoldása. Ez egészen egyszerű, de ez indította el bennem, hogy megpróbáljak (akár már ismert) állításokat az euklideszi-geometriában megismert eszközökkel bizonyítani a hosszú, számolgatós differenciálgeometriás módszer helyett.
Az is motivált, hogy míg a téma nagyon tetszett, a bizonyításokért nem lelkesedtem, a legtöbből nem is értettem semmit, így szerettem volna, ha leírásra kerül ezek egyszerűbb, szemléletesebb levezetése is, amivel akár másoknak is emészthetőbbé tudnám tenni a hiperbolikus geometria témakörét. A folyóirat referee-je is megjegyezte a bírálatában, hogy a közölt módszerem hiánypótló az irodalomban.
A tanáraiddal egyeztettél közben?
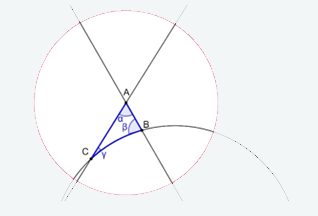
Amikor már megvolt egy körülbelül három oldalas iromány, akkor Hujter Bálint tanár úr véleményét kértem ki, aki biztatott. Azt mondta, hogy ezzel megéri foglalkozni. Majd összekötött dr. Moussong Gáborral, az ELTE adjunktusával, aki azt a problémát adta, hogy a hiperbolikus geometriában három, 180°-nál kisebb összegű szögből mindig szerkeszthető-e háromszög (amelynek tehát a szögei pontosan a megadottak).
És mi a válasz?
Igen, mindig szerkeszthető. Erre egy konstruktív bizonyítást adtam.
Forrás: https://link.springer.com/article/10.1007/s10474-025-01551-1
Ezzel, és még további eredményekkel indultam a BME kari TDK-n, ahol első díjat kaptam, és a Polygon-pályázaton, ahol második díjat nyertem. Ekkor már Koós Krisztiánné Dr. Szilágyi Brigitta volt a BME Algebra és Geometria Tanszékről a témavezetőm. Aztán édesapám segített, hogy a cikknek megfelelő folyóiratot találjunk: az Acta Mathematica Hungarica-ra esett a választásunk. Édesanyám pedig az ábrák esztétikájáért, és az egész cikk – formai szempontból – színvonalasabbá tételéért tett sokat.
Milyen problémán gondolkozol most? Hogyan tovább?
A cikk egyik eredménye volt, hogy karakterizálta, mely n pozitív egész esetén lehet a hiperbolikus síkon egy szakaszt n egyenlő részre osztani. Ugye az euklideszi síkon bármely n-re felosztható, de a hiperbolikus síkon csak a 2-hatványokra.
Ezzel ellentétben a körnégyszögesítés (vagyis, hogy lehet-e egy tetszőleges kör esetén a kör területével megegyező területű négyzetet szerkeszteni) az euklideszi síkon nem lehetséges, viszont én úgy olvastam, hogy a hiperbolikus síkon megoldható. Nagyon szép lenne, ha erre lehetne adni egy elemi, konstruktív bizonyítást.
Pár hónapja elkezdtem készülni a Cambridge-i Egyetem felvételijére, ahol rengeteg számolós feladat van – integrálok, polárkoordináták, mindenfélék. A sok gyakorlás következtében kezdem a matematikának ezeket az ágait megszeretni. Még az is lehet, hogy a végén én is differenciálgeometriával fogok foglalkozni.
Az interjút Paulovics Zoltán készítette.








