Beszámoló a 9. fordulóról
Ebben a fordulóban 11-en küldtek válaszokat, megoldásokat, ezek közül összesen 59 volt helyes. Öten adtak mind a 7 feladatra hibátlan választ. A táblázat fejléce a feladatok számát mutatja, a színes cellák jelentik a jó válaszokat.
\(\bullet\) Building Bridges Between Mathematics and Computer Science, Szerkesztette: Grötschel, Martin; Katona, Gyula O. H.
\(\bullet\) Bessenyei Mihály–Páles Zsolt: Fixponttételek és alkalmazásaik
Megoldások, megjegyzések a Héttusa 9. fordulójának feladataihoz
57. Az 1, 2, 3, 4, 5 számjegyek különböző sorrendjeivel ötjegyű számokat készítünk. Van-e közöttük 9 különböző szám, amelyek beírhatók egy \(3\times 3\)-as táblázatba úgy, hogy minden sorban és minden oszlopban ugyanaz lesz a három szám összege?Javasolta: Berkó Erzsébet (Szolnok)
A válasz: Vannak ilyen számok és van ilyen táblázat.
Megoldás. Dombi Péter a kereséshez helyiértékenként készített \(3\times 3\)-as négyzeteket az 1, 2, 3, 4, 5 számokból (egy-egy négyzetben a sor- és oszlopösszegek azonosak), és ezeket egymáshoz fűzve kapja a táblázat kitöltését. \[\begin{matrix}2&1&2\\1&3&1\\2&1&2\end{matrix}\qquad \begin{matrix}4&2&4\\3&4&3\\3&4&3\end{matrix}\qquad \begin{matrix}3&3&5\\4&5&2\\4&3&4\end{matrix}\qquad \begin{matrix}1&4&3\\2&2&4\\5&2&1\end{matrix}\qquad \begin{matrix}5&5&1\\5&1&5\\1&5&5\end{matrix}\]
Például a fenti négyzetekből kapjuk ezt a jó kitöltést: \[\begin{array}{|c|c|c|@{}}\hline24315&12345&24531\\\hline13425&34521&13245\\\hline23451&14325&23415\\\hline\end{array}\]
Megjegyzés. Ezzel a módszerrel persze kaphatunk olyan táblázatot is, amelyben van két azonos ötjegyű szám. Dombi megad egy sablont, amely alkalmas feltételekkel elkerüli ezt a zsákutcát, és ezen az úton jó ötjegyű számokat lehet generálni.
Megoldás. Berkó Erzsébet nyomán. Ügyes próbálkozással találhatunk ilyen táblázatot.
A közös sor-, oszlopösszeg legyen \(B\). Ha a háromtagú összegekben helyiértékenként nézzük az összegeket, és ezt az öt összeget összeadjuk, az eredmény \(3\cdot (1+2+3+4+5)=45\).
Legyenek az összegek helyiértékenként például 6, 10, 7, 9 és 13, ezekre teljesül, hogy összegük 45. Ekkor \(B=70803\).
\(\begin{array}{|c|c|c|@{}}\hline3\_\,\_\,\_\,\_\,&1\_\,\_\,\_\,\_\,&2\_\,\_\,\_\,\_\,\\ \hline2\_\,\_\,\_\,\_\,&1\_\,\_\,\_\,\_\,&3\_\,\_\,\_\,\_\,\\ \hline1\_\,\_\,\_\,\_\,&4\_\,\_\,\_\,\_\,&1\_\,\_\,\_\,\_\,\\\hline\end{array}\) \(\begin{array}{|c|c|c|@{}}\hline31\_\,\_\,\_\,&15\_\,\_\,\_\,&24\_\,\_\,\_\,\\ \hline25\_\,\_\,\_\,&13\_\,\_\,\_\,&32\_\,\_\,\_\,\\ \hline14\_\,\_\,\_\,&42\_\,\_\,\_\,&14\_\,\_\,\_\,\\\hline\end{array}\)
Folytatva az építkezést, kapunk egy jó táblázatot:
\(\begin{array}{|c|c|c|@{}}\hline31435&15243&24135\\ \hline25143&13245&32415\\ \hline14235&42315&14253\\\hline\end{array}\)
58. Egy kocka egyik csúcsában egy hangya található. A hangya minden nap átmegy az egyik élen egy szomszédos csúcsba. Hány különböző hatnapos vándorlás végződhet az eredeti csúcsban?A válasz: 183.
Megoldás. Helyezzük el a kockát a koordináta-rendszerbe úgy, hogy az \((x,y,z)\) csúcsok \(x,y,z\) komponenseinek értéke 0 vagy 1. Ahol a hangya van, annak a csúcsnak a koordinátái közül az egyik 0-ról 1-re, vagy 1-ről 0-ra változik egy nap elteltével.
A hangya a \((0,0,0)\) csúcsból indul, a hat nap alatt az \(x\) koordináta a-szor, az \(y\) koordináta \(b\)-szer, a \(z\) koordináta \(c\)-szer változik. Ekkor \(a+b+c=6\), mert 6 napig tart az utazás, és \(a,b,c\) mindegyike páros, mert a hangya visszatér a \((0,0,0)\) csúcsba.
Ezeket a feltételeket az \((a,b,c)\) számhármasokból
(1) \((6,0,0)\), \((0,6,0)\), \((0,0,6)\),
(2) \((4,2,0)\), \((4,0,2)\), \((2,4,0)\), \((2,0,4)\), \((0,4,2)\), \((0,2,4)\), és
(3) \((2,2,2)\)
teljesíti.
Az (1) esetben a hangya a kezdő csúcsból induló három él valamelyikét választja, és azon az élen járkál oda-vissza. Ez 3 különböző hatnapos utazás.
Nézzük a (2) esetek közül a \((4,2,0)\)-hoz tartozó lehetőségeket. Az \((x,y,z)\) koordinátákból a hat nap alatt \(x\) 4-szer, \(y\) 2-szer változik. Az \(x,x,x,x,y,y\) karaktereknek \(\dbinom{6}{2}=15\) sorrendje van. A (2) esetekhez tartozó útvonalak száma \(6\cdot 15=90\).
A (3) esetekhez tartozó útvonalakat az \(x,x,y,y,z,z\) karakterek különböző sorrendjei mutatják, ez összesen \(\dbinom{6}{2}\cdot\dbinom{4}{2}=15\cdot 6=90\) lehetőség. Összesen \(3+90+90=183\) különböző hatnapos utazás lehetséges.
Makay Géza megoldása: A kocka csúcsai legyenek a \(\pm 1\) koordinátájú pontokban. Amikor a hangya egy szomszédos csúcsra átmegy, akkor az egyik koordináta az ellentettjére változik, tehát egy lépés a \((-1,1,1)\), \((1,-1,1)\), \((1,1, -1)\) vektorok valamelyikével való koordinátánkénti szorzásnak felel meg. 6 lépéses a vándorlás, de vissza kell térnie a kiinduló csúcsba, így minden ilyen „szorzótényezőnek” páros sokszor kell szerepelnie.
Ha csak egy szorzótényező szerepel hatszor, akkor azt egyféleképpen lehet sorba rakni, ebből akkor 3 lehetőséget kapunk.
Ha egy szorzótényező négyszer szerepel, egy másik kétszer, akkor ezeket \(3\cdot 2=6\)-féleképpen tudjuk kiválasztani, és az ilyeneknek \(\dbinom{6}{2}=15\)-féle sorrendjük van, ebből akkor 90 esetet kapunk.
Végül, ha mindhárom szorzótényező szerepel az úton (mindegyik kétszer), akkor azok még \(\dfrac{6!}{2!\cdot 2!\cdot 2!}=90\)-féle utat adnak, összesen tehát 183-féleképpen vándorolhat a hangya.
Udvari Tibor megoldása: A kocka csúcsait két csoportra oszthatjuk. Négy olyan csúcs van, amelyben páros sok nap után tartózkodhat a hangya, és négy olyan, amelyben páratlan sok lépés után. Jelölje a kiindulási csúcsot \(A\), azokat a csúcsokat pedig, amelyekbe páros sok nap után kerülhet, \(B\), \(C\) és \(D\). A továbbiakban legyen egy lépés kétnapi út. Azt, hogy a különböző csúcsokból melyik csúcsokba és hány lehetséges úton juthat el a hangya, egy ábrával adhatjuk meg:

A továbbiakban \(x\) és \(y\) különböző betűket jelentenek \(B\), \(C\) és \(D\) közül. \(A\)-ból indulva három lépés a következők valamelyikét jelentheti csak:
a) \(A\to A\to A\to A\); b) \(A\to A\to x\to A\); c) \(A\to x\to A\to A\); d) \(A\to x\to x\to A\); e) \(A\to x\to y\to A\).
Az a) eset 27 utat, a b), c) és d) mindegyikének három esete \(3\cdot 12=36\) utat, összesen 108 utat, míg az e) hat esete \(6\cdot 8=48\) utat ad meg. Ezek együtt \(27+108+48=183\) különböző hatnapos utat jelentenek.
Általában, ha \(n\) páros, akkor \(n\) napi vándorlás esetén \(\dfrac{3^n-1}{4}+1=\dfrac{3^n+3}{4}\) különböző út végződhet az eredeti csúcsban. A további három (páros lépésben elérhető) pont mindegyikében \(\dfrac{3^n-1}{4}\) út végződhet.
Az AI (Gemini) megoldása:
Matematikai megközelítés
Ez a probléma a gráfelmélet és a kombinatorika területére tartozik. A kocka csúcsai alkotják a gráf csúcsait, az élek pedig a gráf éleit. A hangya vándorlása lényegében egy séta (walk) a gráfon.
A hangya minden nap átmegy egy szomszédos csúcsba, tehát minden lépésben a hangya az aktuális csúcstól 3 él mentén választhat.
Rekurzív megközelítés
Definiáljuk a következőket:
\(\bullet\) \(a_n\): A hangya \(n\) lépés után az eredeti csúcsban van.
\(\bullet\) \(b_n\): A hangya \(n\) lépés után az eredeti csúccsal szomszédos csúcsok egyikén van (1 élre).
\(\bullet\) \(c_n\): A hangya \(n\) lépés után az eredeti csúcstól 2 élre lévő csúcsok egyikén van.
\(\bullet\) \(d_n\): A hangya \(n\) lépés után az eredeti csúccsal átellenes csúcson van (3 élre).
Tekintsük a lehetséges átmeneteket egy lépésben:
\(\bullet\) Ha a hangya az eredeti csúcsban van (\(a_n\)), akkor a következő lépésben (mindhárom irányba) egy szomszédos csúcsba kerül.
\(\bullet\) Ha a hangya egy szomszédos csúcsban van (\(b_n\)), akkor egy irányba visszamehet az eredeti csúcsba, vagy két irányba mehet egy 2 élre lévő csúcsba.
\(\bullet\) Ha a hangya egy 2 élre lévő csúcsban van (\(c_n\)), akkor két irányba mehet egy szomszédos csúcsba, vagy egy irányba mehet az átellenes csúcsba.
\(\bullet\) Ha a hangya az átellenes csúcsban van (\(d_n\)), akkor (mindhárom irányba) egy 2 élre lévő csúcsba kerül.
Ezeket összegezve kapjuk a következő rekurzív összefüggéseket:
\(a_{n+1}=b_n\) (Minden \(b_n\) állapotból 1 út vezet \(a_{n+1}\)-be.)
\(b_{n+1}=3a_n+2c_n\) (Minden \(a_n\) állapotból 3 út vezet \(b_{n+1}\)-be. Minden \(c_n\) állapotból 2 út vezet \(b_{n+1}\)-be.)
\(c_{n+1}=2b_n+3d_n\) (Minden \(b_n\) állapotból 2 út vezet \(c_{n+1}\)-be. Minden \(d_n\) állapotból 3 út vezet \(c_{n+1}\)-be.)
\(d_{n+1}=c_n\) (Minden \(c_n\) állapotból 1 út vezet \(d_{n+1}\)-be.)
Kezdeti feltételek
\(n=0\). nap: a hangya az eredeti csúcsban van.
\(a_0=1\),
\(b_0=0\),
\(c_0=0\),
\(d_0=0\).
Számítások lépésről lépésre
\(n=1\) nap után:
\(a_1=b_0=0\),
\(b_1=3a_0+2c_0=3\cdot 1+2\cdot 0=3\),
\(c_1=2b_0+3d_0=2\cdot 0+3\cdot 0=0\),
\(d_1=c_0=0\).
\(n=2\) nap után:
\(a_2=b_1=3\),
\(b_2=3a_1+2c_1=3\cdot 0+2\cdot 0=0\),
\(c_2=2b_1+3d_1=2\cdot 3+3\cdot 0=6\),
\(d_2=c_1=0\).
\(n=3\) nap után:
\(a_3=b_2=0\),
\(b_3=3a_2+2c_2=3\cdot 3+2\cdot 6=9+12=21\),
\(c_3=2b_2+3d_2=2\cdot 0+3\cdot 0=0\),
\(d_3=c_2=6\).
\(n=4\) nap után:
\(a_4=b_3=21\),
\(b_4=3a_3+2c_3=3\cdot 0+2\cdot 0=0\),
\(c_4=2b_3+3d_3=2\cdot 21+3\cdot 6=42+18=60\),
\(d_4=c_3=0\).
\(n=5\) nap után:
\(a_5=b_4=0\),
\(b_5=3a_4+2c_4=3\cdot 21+2\cdot 60=63+120=183\),
\(c_5=2b_4+3d_4=2\cdot 0+3\cdot 0=0\),
\(d_5=c_4=60\).
\(n=6\) nap után:
\(a_6=b_5=183\),
\(b_6=3a_5+2c_5=3\cdot 0+2\cdot 0=0\),
\(c_6=2b_5+3d_5=2\cdot 183+3\cdot 60=366+180=546\),
\(d_6=c_5=0\).
Válasz: A hangya 6 napos vándorlása \(a_6=183\) különböző módon végződhet az eredeti csúcsban.
59. Egy szabályos háromszöget kilenc egybevágó háromszögre osztottunk, és ezekbe mint cellákba 0-kat írtunk. Ezután egy-egy lépésben kiválasztunk két, oldalban szomszédos cellát, és az ottani két számot vagy 1-gyel nagyobbra, vagy 1-gyel kisebbre cseréljük. Az a célunk, hogy ilyen lépésekkel eljussunk olyan kitöltéshez, amikor 9 egymást követő pozitív egész szám, \(n+1\), \(n+2\), \(n+3\), …, \(n+9\) van a háromszög celláiban. Hány olyan \(n\) egész szám van, amelyre ez elérhető?A válasz: 1.
Megoldás. Kezdetben a számok összege 0, ez az összeg minden lépésben 2-vel változik. Ez azt jelenti, hogy az összeg mindig páros, így a 45-ös összegű 1, 2, …, 9 számok nem kaphatók meg.
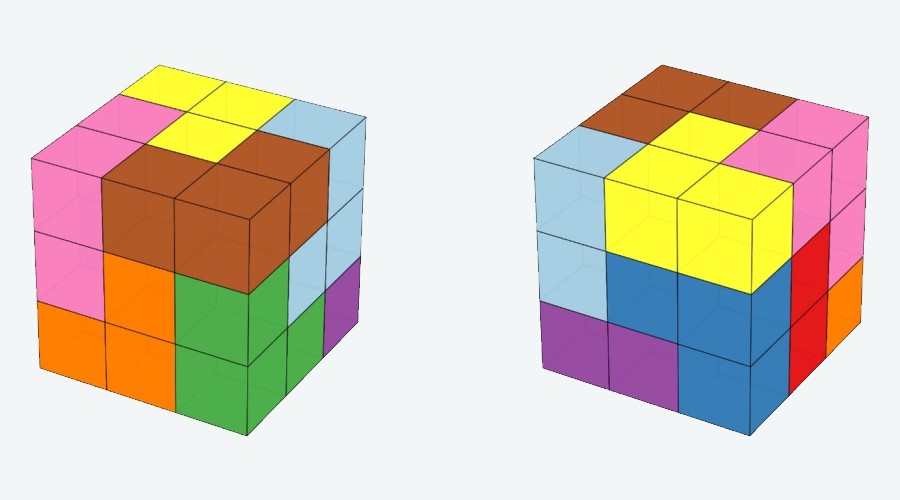
A 2, 3, …, 10 számok összege 54, ez páros, ezeknek a számoknak van esélye. Az ábrán látjuk, hogy ez a lehetőség megvalósítható.

Az első három háromszög mutatja, hogy szomszédos cellapárokban hányszor növeljük a számokat 1-gyel. Ha ezeket a lépéseket mind elvégezzük, megkapjuk a jobb szélső ábrán lévő kitöltést, amelyben 9 egymást követő szám áll.
Belátjuk, hogy ez az egyetlen elérhető olyan kitöltés, amelyben 9 egymást követő pozitív egész szám áll.
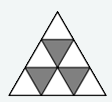
Színezzük a háromszögeket az ábrán látható módon. Egy lépésben egy fehér és egy fekete cellában változtatjuk meg az ottani számot. Kezdetben a fekete és a fehér mezőkben a számok összege ugyanaz, mindkét összeg 0. Egy lépésben mindkét összeg ugyanúgy változik, ezért a fekete és a fehér mezőkben a számok összege mindig ugyanannyi.
Ha a háromszögben 9 egymást követő pozitív egész szám van, \(n+1,n+2,\ldots ,n+9\), ahol \(n\ge 0\), akkor a fehér mezőkben a számok összege \[V\ge (n+1)+(n+2)+(n+3)+(n+4)+(n+5)+(n+6)=6n+21;\] a fekete mezőkben a számok összege \[S\le (n+7)+(n+8)+(n+9)=3n+24.\] A két összeg egyenlő, \(V=S\).
Ezek miatt: \(6n+21\le V=S\le 3n+24\), azaz \(6n+21\le 3n+24\), tehát \(n\le 1\), így \(n=0\) vagy 1. Láttuk, hogy ebből a két lehetőségből csak a másodikhoz tartozó kitöltés valósul meg.
60. Egy síkon felvettünk 12 különböző pontot, majd pirosra festjük a pontpárokat összekötő szakaszok felezőpontját. Legkevesebb hány pontot festünk pirosra?A válasz: 21.
Udvari Tibor megoldása: Keressük meg a pontok közötti távolságok legnagyobbikát, legyen ez \(d\). Válasszuk ki az egymástól legtávolabb levő két pontot, \(A\)-t és \(B\)-t. (Ha több pont is van a legnagyobb távolsággal, akkor valamelyik kettőt.) Mindkettő a többi ponttal 11 szakaszt alkot, amelyek egyik végpontja közös. Ezeknek a szakaszoknak különbözőek a másik végpontjaik, ezért a szakaszfelező pontjaik is. A többi pont az \(A\) körüli \(d\) sugarú körön belül vagy a határán van, ezért a felezőpontok az \(A\) körüli \({d}/{2}\) sugarú körön belül vagy a határán. Ugyanez igaz \(B\)-re is. A két \({d}/{2}\) sugarú kör egy pontban, az \(AB\) felezőpontjában érinti egymást, ez a pont kétszer is piros színt kap. Más szakaszfelezők nem lehetnek azonosak. Így \(2\cdot 11-1=21\) piros pontunk biztosan lesz. Ezt el is tudjuk érni, ha a 12 pont egy egyenesen, egymástól egyenlő távolságra van. (Válasszuk a számegyenesen a 2, 4, 6, …, 24 számokat. Ha ezt a 12 pontot nézzük, a közöttük lévő szakaszoknak 21 különböző felezőpontja van, ezek 3, 4, 5, …, 23.)
Általában, ha \(n\) pontunk van, akkor legalább \(2n-3\) piros pontunk lesz és az egy egyenesen, egymástól egyenlő távolságra elhelyezett pontokkal meg is valósítható ennyi piros pont.
Megjegyzés: Érdemes elolvasni Pintér Lajos cikkét a Polygon-ban, amelyben a 10. példa épp az általános \(n\) pontos eset, és a megoldás gondolatmenete is a fenti: https://www.math.u-szeged.hu/polygonlap/p129.pdf.
Dombi Péter az előbbi általános állítást teljes indukcióval bizonyítja, és ad egy másik bizonyítást is:
Vegyünk egy olyan egyenest, amire a pontok merőleges vetülete mind különböző. Mivel a felezőpont vetülete a vetületek felezőpontja, elég az állítást a számegyenesen igazolni, azaz elég belátni, hogy \(n\) darab \(x_i\) szám közül legalább \(2n-3\) párnak különböző a számtani közepe. Ha \(x_1<x_2<\ldots <x_n\), akkor az \[\dfrac{x_1+x_2}{2}<\dfrac{x_1+x_3}{2}<\ldots<\dfrac{x_1+x_n}{2}<\dfrac{x_2+x_n}{2}<\dfrac{x_3+x_n}{2}<\ldots<\dfrac{x_{n-1}+x_n}{2}\] átlagok mind különbözők, és a számuk \(2n-3\).
https://math.stackexchange.com/questions/4590494/minimum-number-of-midpoints
61. Ottó a hatoslottón nyolc szelvényt töltött ki, mindegyiken hat számot jelölt meg az 1, 2, …, 45 számokból. Egy számot több szelvényen is megjelölhet, de nincs két olyan szám, amelyeket együtt egynél több szelvényen is megjelöl. Legkevesebb hány különböző szám van ezen a nyolc szelvényen?A válasz: 23.
Makay Géza megoldása: Kezdjük el kiosztani a számokat a szelvényekre „optimálisan”, vagyis minden újabb szelvényen legyen egy-egy szám a korábbi szelvényekről, és annyi új szám, hogy az kiadja a szelvényenkénti 6 számot:
\((1,2,3,4,5,6)\) \((1,7,8,9,10,11)\) \((2,7,12,13,14,15)\) \((3,8,12,16,17,18)\) \((4,9,13,16,19,20)\) \((5,10,14,17,19,21)\) \((6,11,15,18,20,21)\)
Az eddig felhasznált számok mindegyike két szelvényen szerepel. Így az utolsó szelvényre ezek közül legfeljebb 3-at választhatunk ki, mert különben lenne egy számpár két szelvényen is, tehát a nyolcadik szelvény például ez lehet: \((1,12,19,22,23,24)\). Így a különböző számok minimumára van egy 24-es felső becslésünk.
Ha egy szám öt szelvényen is szerepel, akkor az azokon a szelvényeken levő többi számnak egymástól különbözőnek kell lenniük, ez már legalább \(5\cdot 5+1=26\) különböző számot jelentene.
Ha egy szám négy szelvényen is szerepel, akkor a maradék szelvényeken az nem szerepelhet, a többi számból minden szelvényről csak 1-1 szám jöhet szóba, így a maradék szelvényeken kell lennie legalább két számnak, amelyek eddig még nem szerepeltek.
Ugyanaz a két szám nem szerepelhet a maradék szelvényeken, mert akkor az a számpár több szelvényen is szerepelne, tehát legalább 3 újabb számról beszélünk, és akkor a számok száma legalább \(1+4\cdot 5+3=24\) lenne. Így csak az az eset marad, hogy minden szám legfeljebb 3 szelvényen szerepel, a fenti példánk is ilyen.
Próbáljuk meg kicsit tömöríteni a számokat, lehetőleg minden szám 3 szelvényen szerepeljen. Kis kísérletezés után például erre az eredményre juthatunk:
\((1,2,3,4,5,6)\) \((1,7,8,9,10,11)\) \((1,12,13,14,15,16)\) \((2,7,12,17,18,19)\) \((2,8,13,20,21,22)\) \((3,9,14,17,20,23)\) \((4,10,15,18,21,23)\) \((5,11,16,19,22,23)\)
Vajon meg lehet-e oldani a feladatot 22 számmal is? Ekkor, ha minden számot kétszer számolok, akkor 44 számunk van, a 8 szelvényen összesen 48 szám kell, úgyhogy legalább 4 szám háromszor fog szerepelni, legyenek ezek az 1, 2, 3, 4 számok. Bármelyik két hármashoz csak egyetlen szelvény tartozhat, amelyen mindkét szám szerepel, és mivel a négy darab hármas összesen 12 szám, kell is, hogy legyen átfedés a hármasok között. Feltéve, hogy az 1-es és 2-es számok között van átfedés, töltsük ki a szelvényeket a következő sorrendben: előszőr az 1-eseket tartalmazó szelvényeket, aztán az 1-es és 2-est tartalmazó szelvény, utána a maradék két szelvényt, ami 2-eseket tartalmaz, és azután a többit. Számoljuk meg, hogy kitöltés közben hány új számot kell felhasználnunk. Az első szelvényen 6-ot, a következő kettőn 5-öt (hiszen az 1-es már közös a szelvényeken). A rákövetkező kettőn 2-es van, a harmadik szelvényről nem választhatunk számot, csak az első kettőről, így ott minimum 3-3 új szám kell. Végül a hatodik szelvényen is kell egy új számjegy, hiszen az első öt szelvényről csak 1-1 számot választhatunk. Ez összesen \(6+5+5+3+3+1=23\) szám, ami ellentmond annak, hogy 22 számmal oldanánk meg a feladatot. Tehát 23-nál kevesebbel a feladat nem megoldható. Vegyük észre, hogy a fenti példában is teljesül, hogy a hatodik szelvényig bezárólag már leírtuk az összes felhasznált számot.
Udvari Tibor megoldása: Mind a 8 darab szelvényen 6 számot kell bejelölni. Ez összesen 48 bejelölt szám. Ha minden számot két különböző szelvényen használunk fel, akkor 24 különböző szám lesz a nyolc szelvényen. Ilyen például az alábbi nyolc szelvény:
\((1,8,9,15,17,22)\), \((1,2,10,16,18,23)\), \((2,3,9,11,19,24)\), \((3,4,10,12,17,20)\), \((4,5,11,13,18,21)\), \((5,6,12,14,19,22)\), \((6,7,13,15,20,23)\), \((7,8,14,16,21,24)\).
Lehet-e 23 számmal is kitölteni úgy, hogy egy számot kettőnél több szelvényen használunk fel? Ha igen, akkor valamelyik számnak kettőnél több szelvényen kell szerepelnie. Ha egy szám három különböző szelvényen szerepel, akkor azokon a szelvényeken a továbbiaknak már csupa különböző számnak kell lennie. Tehát így 16 különböző számot biztosan használunk. A maradék öt szelvény mindegyikén szerepelhet egy a három szelvényről: a mindhárom szelvényen szereplő számon kívül bejelölt öt szám egyike. Ez együtt 33 bejelölt szám, 15 szám kétszer, egy pedig háromszor. Mivel még \(48-33=15\) bejelölés kell és \(23-16=7\) számot használhatunk fel, lesz még olyan szám, amelyet kettőnél többször használunk. Használjuk megint az egyiket háromszor. Egy kis próbálkozással megtalálható például a nyolc szelvény alábbi kitöltése 23 különböző számmal:
\((1,2,3,4,5,6)\), \((1,7,8,9,10,11)\), \((1,12,13,14,15,16)\), \((2,7,12,17,18,19)\), \((3,8,13,17,20,21)\), \((4,9,14,17,22,23)\), \((5,10,15,18,20,22)\), \((6,11,16,19,21,23)\).
Próbálkozhatunk azzal is, hogy háromnál több szelvényen legyen valamelyik szám. Gyorsan látható, hogy már öt szelvény esetén legalább 26 számra lenne szükség. Ha négy szelvényen van közös szám, akkor 21 szám mindenképpen kell és a maradék négy szelvényre ezek közül legfeljebb 4-4, összesen 16 kerülhet fel.
Ez \(24+16=40\) bejelölés, és a hiányzó 8-at a \(23-21=2\) számból kellene teljesíteni a 4 szelvényen. Ezt nem tehetjük meg ismétlődő párok nélkül.
Az előző gondolatmenetekből adódik az is, hogy 22 vagy kevesebb szám felhasználásával a kitöltés nem hajtható végre.
Dombi Péter megoldása: Legalább 23 szám lesz a nyolc szelvényen. Ha csak 22 számot használunk, akkor először is egyszerű fokszám-okoskodással látszik, hogy valamelyik szám három szelvényen is szerepel, hiszen \(22\cdot {2}/{6}\) csak 7 szelvényt engedne meg. Legyen például az 1-es szám az első három szelvényen, ezen a három szelvényen több közös szám nem lehet, így feltehetjük, hogy az első 16 szám van rajtuk: \[L_1=\{1;2;3;4;5;6\}, L_2=\{1;7;8;9;10;11\}, L_3=\{1;12;13;14;15;16\}.\] A skatulyaelv miatt a többi szelvényen legfeljebb 3 szám lehet a fentiek közül, így az \(L_i\setminus (L_1\cup L_2\cup L_3)\), (\(i=4,\ldots,8\)) öt hármas a maradék, \(\{17,\ldots,22\}\) hat számon 3-as lottót játszana ugyanúgy, legfeljebb egy egyezést engedve. Ismét fokszámindoklással, \(6\cdot {2}/{3}<5\) miatt ez csak akkor lehetne, ha valamelyik szám 3 hármasban is szerepelne, viszont az a 3 csillagszerű hármas már 7 számot tartalmazna, ami hatelemű halmazon nyilván ellentmondás. Ottó 23 számmal a következő szisztémát játszhatja: \[\begin{array}{@{}l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{\;\ }l@{}} 1&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16&17&18&19&20&21&22&23\\ \hline 1&2&3&4&5&6\\ 1& & & & & &7&8&9&10&11\\ &2& & & & &7& & & & &12&13&14&15&16\\ \hline\\ & &3& & & & &8& & & & &13& & & &17&18&19\\ & & &4& & & & &9& & & & &14& & &17& & &20&21\\ & & & &5& & & & &10& & & & &15& & &18& &20& &22\\ & & & & &6& & & & &11& & & & &16& &18& & &21& &23\\ \hline \end{array}\] Látható, hogy \(23\cdot{2}/{6}<8\) miatt itt is kell harmadfokú pont, az erre a pontra csillagszerűen illeszkedő 3 szelvényt mutatja az első 3 sor. A maradék 5 szelvény ezt a 3 hatost egy-egy pontban „körbemetszi”, egymással pedig a \(\{17,\ldots, 23\}\) hételemű halmazon, a tábla jobb alsó részében az 5 hármas úgy viselkedik, hogy könnyű bennük felismerni a Fano-sík 5 egyenesét (olyan 5 hármast, amit az indirekt bizonyítás végén 6 elemű halmazon nem lehetett felvenni).
Turchányi Gyula faggatta a feladatokról az AI-t, erről olvasható cikke a Héttusa rovatban: Hogyan használtam az AI-t a Héttusa-feladatok megoldásaihoz?
A lottószelvényeken szereplő számok számára az AI adott egy gyenge és egy erős becslést is. Ezeket a bizonyításokat leírtam gördülékenyebben.
A gyenge becslés. Minden szelvényen 6 szám van, a szelvényeken összesen \(8\cdot\dbinom{6}{2}=8\cdot 15=120\) különböző számpárt látunk. Ha összesen \(n\) darab különböző szám szerepel a szelvényeken, akkor az ezekből képezhető számpárok száma emiatt legalább 120, azaz \(\dbinom{n}{2}\ge120\), \(n\ge 16\).
Legalább 16 különböző szám van a szelvényeken.
Az erős becslés. A szelvényeken \(n\) darab különböző szám szerepel, és az \(i\)-edik számot a szelvényeken \(r_i\) alkalommal látjuk.
\(r_1+r_2+\ldots+r_n=6\cdot 8=48\), hiszen az összegzéssel megszámoljuk a szelvényeken lévő számokat.
Két szelvényen legfeljebb 1 közös szám lehet a feltétel miatt. Legyen \(N\) azon szelvénypárok száma, amelyekhez tartozik közös szám. \(N\le\dbinom{8}{2}=28\).
Egy adott szám, amely \(r_i\)-szer fordul elő, éppen \(\dbinom{r_i}{2}\) ilyen szelvénypárt generál, tehát \[\dbinom{r_1}{2}+\dbinom{r_2}{2}+\ldots+\dbinom{r_n}{2}=N.\]
\(r_i^2=r_i+2\dbinom{r_i}{2}\), ezért \begin{gather*} r^2_1+r^2_2+\ldots +r^2_n=\left(r_1+r_2+\ldots +r_n\right)+2\dbinom{r_1}{2}+\dbinom{r_2}{2}+\ldots +\dbinom{r_n}{2}=\\ =48+2N\le 48+2\cdot 28=104. \end{gather*} Használjuk a számtani és a négyzetes közepek közötti egyenlőtlenséget: \[\frac{r^2_1+r^2_2+\ldots +r^2_n}{n}\ge {\left(\frac{r_1+r_2+\ldots +r_n}{n}\right)}^2,\] azaz \[\frac{104}{n}\ge {\left(\dfrac{48}{n}\right)}^2.\] Rendezés után \(n\ge \dfrac{{48}^2}{104}>22\). Tehát a szelvényeken legalább 23 különböző szám szerepel.
62. A LogikuSakk Egyesület edzőtábort szervez 16 sakkozójának, ahol minden játékosra 3 mérkőzés vár, és ezt a beosztást, hogy ki kivel fog játszani, már elkészítették. Igaz-e, hogy az előírt edzőmérkőzések lebonyolíthatók 3 nap alatt úgy, hogy senki sem játszik 1-nél több mérkőzést naponta?A válasz: Nem igaz.
Berkó Erzsébet megoldása: Van olyan beosztás, amikor 3 nap alatt nem lehet lejátszani az edzőmérkőzéseket.

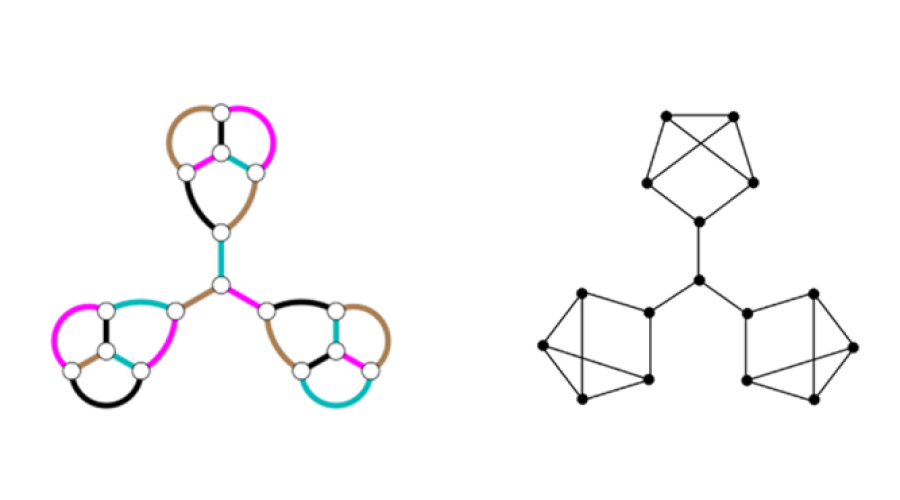
Ennek a 3-reguláris síkba rajzolható gráfnak 16 csúcsa és 24 éle van, de a maximális elemszámú párosításai csak 7 élt tartalmaznak. Ezért élszínezéséhez négy színre van szükség.
(A két gráf azonos. A játékosokat a gráf csúcsai jelölik, és egy játékos azokkal fog játszani, akikkel él köti össze. A középpontban álló játékos a beosztás szerinti 3 ellenfele közül valamelyikkel játszik, de ekkor a másik két ellenfél ötös csoportjában nem játszhat mindenki az első napon, mert az 5 sakkozóból valakinek nem jut pár.)
Udvari Tibor megoldása: A versenyzőket és a mérkőzéseket egy gráf 16 csúcsa és 24 éle jelképezze. A gráf minden csúcsának 3 a fokszáma. Nézzük az alábbi gráfot.

Egy nap legfeljebb 8 mérkőzés lehet a 16 játékos részvételével, ha senki sem játszik egynél több mérkőzést naponta. Így a 24 mérkőzést 3 nap alatt akkor lehet lejátszani, ha minden nap pontosan 8 mérkőzést rendeznek. Ez azt jelenti, hogy a gráfot 3 elsőfokú faktorra kell felbontani. Ez a bal oldali részgráfnál nem valósítható meg (lásd pl. Andrásfai Béla: Ismerkedés a gráfelmélettel, 5. fejezet, 39. feladat megoldása), így a teljes gráfban sem.
Dombi Péter megoldása: Nem, nem mindig lehet ilyen lebonyolítást találni. A következő ábrán látható beosztást például azért nem lehet megvalósítani, mert azon a napon, amikor a megjelölt pár (\(AB\)) játszana egymással, akkor a CDE hármasból valaki biztos ki fog maradni. Ehhez hasonló beosztás minden \(n\ge 10\) páros szám esetén készíthető, a 11-szög helyett más, 5 vagy annál nagyobb páratlan oldalú sokszöget használva, hasonló párosítással, mivel a napi fordulókra való szétosztást az \(ABCDE\) rész párosítása teszi lehetetlenné.

Adható más szerkezetű ellenpélda is, a Petersen-gráf felhasználásával. Az alábbi ábra bal oldala mutatja a 10 csúcsú Petersen-gráfot, a szokásostól kicsit eltérő ábrázolásban, az \(ABQKP\) az egyik (pl. „külső”), és \(TRA’SB’\) a másik ötszög.

Belátjuk, hogy ha ilyen részgráfot tartalmaz a sorsolás, akkor szintén nem lehet 3 fordulóba szétosztani a mérkőzéseket. Tekintsük most is azt a napot, amikor \(A\) és \(B\) játszanak egymással. Ezen a napon a többi 8 játékos egymással játszik, tehát töröljük \(A\)-t és \(B\)-t, a hozzájuk tartozó élekkel. Így egy nyolcas kört kapunk, két nagy (\(KS\), \(RT\)) átlóval, ez látszik a jobb oldali ábrán (a \(K\) csúcsot „lehúztuk alulra”, hogy látszódjon a nyolcszög teljes szimmetriája). A letisztított ábrán látjuk, hogy \(A’\) aznap vagy \(R\)-rel, vagy \(S\)-sel játszhat. Ha pl. \(S\) ellen játszik, akkor ez már a nyolcszögön a forduló többi mérkőzését is meghatározza: (\(B’T\)), (\(PK\)) és (\(QR\)).
Így a másik két napra marad a zölddel jelölt 6 él, valamint \(A\) és \(B\) le nem játszott 2-2 mérkőzése. Vegyük észre, hogy a zöld élek szétesnek két összefüggő részre, méghozzá pont úgy, hogy az egyik út \(A’\) és \(P\) végpontja az \(A\)-nak, a másik út \(B’\) és \(Q\) végpontja \(B\)-nek volt kisorsolva. Vagyis arra a két napra két, közös pont nélküli 5-ös csoport (ciklus) alakul ki. Mivel a csoportok között nincs már mérkőzés, páratlan elemű csoporton belül valakinek nem lesz párja.
A 10 elemű ellenpéldából könnyen kaphatunk \(n\ge 14\) résztvevős ellenpéldát, csak ki kell egészíteni bármilyen 3-reguláris komponenssel, például egy \(2k\) elemszámú „kerékkel”, azaz egy szabályos \(2k\)-szöggel, ahol minden csúcs a szomszédos és a szemköztes csúccsal van összekötve.
https://en.wikipedia.org/wiki/Petersen_graph
https://en.wikipedia.org/wiki/Snark_(graph_theory)
63. A tér minden egyes pontja öt szín egyikével van színezve, és a színezéshez mindegyik színt felhasználtuk. Igaz-e, hogy mindig van olyan sík, amelyen legalább 4 szín szerepel?A válasz: Igaz.
Makay Géza megoldása: Ha van olyan egyenes, amin legalább 3 különböző szín is szerepel, akkor ehhez hozzávéve egy ezektől különböző színű pontot, az egyenes és a pont meghatároznak egy olyan síkot, amin legalább 4 különböző szín van. Vagyis, ha nem igaz az állítás, akkor minden egyenesen legfeljebb 2 különböző színű pont lehet.
Vegyünk három különböző színű pontot, ezek akkor nincsenek egy egyenesen, meghatároznak egy \(S\) síkot. Vegyünk a maradék két színből egy-egy pontot, azok meghatároznak egy egyenest. Ha a síknak és az egyenesnek lenne közös pontja, akkor azt a sík miatt csak az első három szín valamelyikére lehetne színezni, az egyenes miatt viszont csak az utóbbi két szín egyikére, amiből ellentmondásra jutnánk. Így tehát a sík és az egyenes párhuzamos kell legyen, amiből következik, hogy az utóbbi kétféle színű pontok mindegyike az \(S\) síkkal párhuzamos síkon kell legyen. Ezt bármelyik színpárra be tudjuk látni, amivel azt is bebizonyítottuk, hogy az összes színezett pont az \(\dbinom{5}{2}=10\) színpár által meghatározott 10 sík valamelyikén kell legyen. 10 sík viszont nem adja ki a teljes teret, ellentmondásra jutottunk. Tehát kell legyen olyan sík, amelyiken legalább 4 különböző színű pont van.
Udvari Tibor megoldása: Tegyük fel, hogy sikerült úgy kiszínezni a teret, hogy bármelyik síkon legfeljebb 3 szín szerepel.
Jelölje az öt színt \(A\), \(B\), \(C\), \(D\) és \(E\). Mivel mindegyik színt felhasználtuk, ki tudunk választani öt pontot, amelyek ezekkel a színekkel vannak színezve. Nézzük azt a két síkot, amelyet az \(A\), \(B\), \(C\), illetve az \(A\), \(D\), \(E\) színű pontok alkotnak. A két síknak van közös pontja (az \(A\) színű) és nem esnek egybe (mert akkor 5 szín lenne egy síkon). Ezért van egy közös egyenesük. Ennek egyik pontja az \(A\) színű pont. De ennek az egyenesnek minden más pontja is biztosan \(A\) színű. Ellenkező esetben az előbbi két sík egyikén lenne egy negyedik színű pont.
Nézzük most a \(B\), \(C\), \(D\), a \(B\), \(C\), \(E\), a \(B\), \(D\), \(E\) és a \(C\), \(D\), \(E\) színű pontok alkotta négy síkot. Bármelyik kettőnek van két közös pontja és semelyik kettő nem lehet azonos sík (mert lenne 4 színnel színezett síkunk). Ezért a négy sík egy tetraéder négy lapsíkja.
Egy egyenes nem lehet egy tetraéder mind a négy lapsíkjával párhuzamos, így az előbbi egyenesünknek van közös pontja valamelyik lapsíkkal. Ennek a közös pontnak a színe egyrészt \(A\) lenne (az egyenes miatt), másrészt a maradék négy szín valamelyike (a lapsík három színéből az egyik). Ez ellentmondás, így feltételezésünk hibás. Tehát mindenképpen kell lennie olyan síknak, amelyen legalább 4 szín szerepel.
Dombi Péter (egyik) bizonyítása: Igen, mindig lesz legalább 4-színű sík. Csak 4 színt használva viszont el lehetne kerülni. Vegyünk fel egyre bővülő affin altereket, például valamilyen koordinátarendszerben az origót fessük pirosra, az \(x\) tengely többi pontját kékre, az \(xy\) sík többi pontját zöldre, a tér többi pontját lilára. Ennél a színezésnél minden egyenes legfeljebb 2-színű, és minden sík legfeljebb 3-színű.
A feladathoz elég belátni azt a – valójában ekvivalens – állítást, hogy ha mind az 5 színt felhasználjuk, akkor mindig lesz legalább 3-színű egyenes. Először lássuk be az ekvivalenciát. A feltétel elégséges, mert ha van 3-színű egyenes, akkor egy negyedik színű pontot és a 3-színű egyenest tartalmazó sík már 4-színű. De fordítva is igaz, mert ha valamelyik síkban van 4 különböző színű pontunk, akkor ha ebből 3 kollineáris, akkor ez egy 3-színű egyenes, ha nem, akkor valamelyik két pont egyenese metszi a másik két pont egyenesét, így ha az első egyenes az 1. és 2. színű, a másik a 3. és 4. színű pontokra illeszkedett, akkor a metszéspont akármilyen színű is, e két egyenes valamelyikét háromszínűvé teszi.
A következőkben belátjuk, hogy nem lehet a teret 5 színnel kiszínezni úgy, hogy minden egyenes legfeljebb kétszínű legyen. Legyen \(P\) piros, \(Q\) kék és \(R\) rózsaszínű pont, amikről feltehetjük, hogy nem kollineárisak. Az előző bekezdésben látottak miatt azt is feltehetjük, hogy a \(PQR\) síkon csak ez a három szín fordul elő. Legyen \(S\) sárga és \(T\) türkiz pont a \(PQR\) síkon kívül. Ha az \(ST\) egyenes metszi a \(PQR\) síkot, akkor készen vagyunk: a metszéspont vagy a \(PQR\) sík negyedik, vagy az \(ST\) egyenes harmadik színű pontja lenne. Tehát \(ST\) párhuzamos a \(PQR\) síkkal. A \(PQR\) háromszögnek van olyan oldala, amelyikkel az \(ST\) nem párhuzamos, legyen ez a \(PQ\) oldal. Húzzunk a szemközti \(R\) csúcson át az \(ST\)-vel párhuzamos egyenest, ez metszeni fogja a \(PQ\) oldalegyenest (hisz a csúcsot pont így választottuk), legyen a metszéspont \(M\). Ez az \(M\) egyrészt eleme lenne a csak piros és kék színekkel színezett \(PQ\) egyenesnek, másrészt a csak rózsa, sárga és türkiz színekkel színezett \(RST\) síknak, ami lehetetlen.
Róka Sándor, a Héttusa rovat vezetője