A cikk szerzője a Héttusa verseny aktív és eredményes feladatbeküldője, a megoldásaihoz rendszeresen igénybe veszi a mesterséges intelligencia különböző változatait. Bár érettségiig magas szintű zenei és matematikai képzésben is részesült, végül informatikával foglalkozó mérnök lett. Immár nyugdíjasként rengeteg (és vegyes) tapasztalatra tett szert a ChatGpt, a Gemini, a DeepSeek, vagy a Grok alkalmazásáról matematikai vagy műszaki problémák megoldásában, programkódok készítésében. A Héttusa legutóbbi feladatsorán mutatja be saját és az AI ötleteit, valamint azt, hogy ezt miként lehet kombinálni, ezzel az AI-t jobb válaszok készítésére bírni, s mennyire fontos a válaszok ellenőrzése.
57. Az 1, 2, 3, 4, 5 számjegyek különböző sorrendjeivel ötjegyű számokat készítünk. Van-e közöttük 9 különböző szám, amelyek beírhatók egy \(3\times 3\)-as táblázatba úgy, hogy minden sorban és minden oszlopban ugyanaz lesz a három szám összege?
Válasz: van.
Indoklás: Bár könnyű lett volna kézzel is találni megoldást, gondoltam, íratok egy programot a mesterséges intelligenciával, ami megkeresi az összeset. Az első utasításomra olyan kódot kaptam, amely \(3\;794\;488\;348\;147\;660\;800\) esetet (a legenerálható számok valamennyi 9-es csoportjának száma) akart megvizsgálni. Mivel a határidőt nem a napunk vörös óriássá alakulása utánra tűzték ki, ezt az algoritmust eldobtam, és adtam a gépnek pár ötletet, mitől lehetne gyorsabban keresni. Arra is megkértem, hogy ne sorolja fel azokat a megoldásokat, amelyek egyszerű átrendezésekkel egymásba transzformálhatóak. Ennek alapján működő kódot kaptam minden további segítség nélkül. Nem volt szuper gyors, de kit érdekel, tulajdonképpen egy találat után is leállíthattam volna, én mégis kértem, hogy az összeset keresse meg, mert kíváncsi voltam rá, hány van.
510 másodperc után kiderült, hogy összesen \(13\;520\) darab, precízen definiált alapmegoldás létezik. (Alapmegoldás, amikor két megoldás nem vihető át egymásba sorok/oszlopok cseréjével és transzponálással.)
Az összeg maga is 2040-féle lehet, és vannak olyan összegek, amelyek mögött 58-féle megoldást találunk (120 ilyen van). Példaként megmutatom a legkisebb összeget, \(49\;023\)-at eredményező megoldást: \[\begin{array}{|l|l|l|} \hline 12345&15243&21435\\ \hline 15324&21345&12354\\ \hline 21354&12435&15234\\ \hline \end{array}\]
Van-e köztük valódi bűvös négyzet – jutott eszembe a következő kérdés. Azaz van-e olyan négyzet, amikor az átlók is ugyanazt az alapösszeget adják. Ehhez bővítettem az eredeti programot. Csak a már megtalált megoldásokat vizsgáltam. Ahhoz, hogy ez teljesüljön, az összegnek 3-mal oszthatónak kell lennie, és a táblázat középső mezőjében ennek az összegnek a harmada áll. (Ha van ilyen szám a táblázatban, azt sor/oszlop cserékkel középre lehet vinni.) Ha a kódom jó – annak tűnik –, akkor nincs ilyen megoldás, amin azért nem lepődtem meg különösebben az erős megkötések miatt.
A kódot kitettem a github oldalamra.
58. Egy kocka egyik csúcsában egy hangya található. A hangya minden nap átmegy az egyik élen egy szomszédos csúcsba. Hány különböző hatnapos vándorlás végződhet az eredeti csúcsban?
Válasz: 183.
Indoklás: Ezt a feladatot sokféle módon megoldottam, pontosabban alapötleteket dolgoztattam ki a mesterséges intelligenciával, majd az így kapott eredményt értékeltem, átolvastam, átszerkesztettem. A megoldások alapötlete tőlem származott, a kidolgozásban és megjelenítésben használtam mesterséges intelligenciát.
Legjobban ezt a táblázatos megoldást szeretem. A megoldás szövegét rövidítettem, remélhetőleg emberibbre, azaz ember által könnyebben emészthetővé alakítottam.

A táblázatot soronként haladva töltjük ki. A táblázat értelmezése: a kocka egyes csúcsait 3-jegyű bináris kódok jelölik, ezek adják a táblázat fejlécét. Az egymás melletti oszlopok csupán egy bittel térnek el egymástól (az utolsó és az első oszlop is szomszédos). Egy csúcsnak azonban 3 szomszédja van 1 bit távolságra, a harmadik szomszéd a vele azonos színű oszlopban található.
A 0. napon a hangya a 000 csúcson van. Az egyes sorok azt fejezik ki, hogy az adott napon hányféle módon lehet megérkezni az adott csúcsra. Ehhez az 1. naptól kezdve a felette lévő sor két szomszédos elemét, s az oszlopunk színével egyező harmadik számot kell összeadni. Példaként: a megoldást adó 183 a bekeretezett 3 szám összege. A táblázat minden sora így készült.
Merőben más megközelítéssel is ugyanezt az eredményt kaptam, és ez megnyugtató volt.
59. Egy szabályos háromszöget kilenc egybevágó háromszögre osztottunk, és ezekbe, mint cellákba 0-kat írtunk. Ezután egy-egy lépésben kiválasztunk két, oldalban szomszédos cellát, és az ottani két számot vagy 1-gyel nagyobbra, vagy 1-gyel kisebbre cseréljük. Az a célunk, hogy ilyen lépésekkel eljussunk olyan kitöltéshez, amikor 9 egymást követő pozitív egész szám, \(n+1, n+2, \ldots, n+9\) van a háromszög celláiban. Hány olyan \(n\) egész szám van, amelyre ez elérhető?
Válasz: 1 (\(n=1\)).
Indoklás: A feladatot amellett a valószínűleg igaz – de általam nem bizonyított – feltevés mellett oldottam meg, miszerint egy szabályos háromszöget csak egyféle módon lehet 9 egybevágó háromszögre bontani. Könnyíthette volna a feladatot egy ábra, vagy a „kilenc egybevágó szabályos háromszögre osztottuk” megfogalmazás.
Osszuk a 9 egybevágó háromszöget két csoportba: a nagy háromszög csúcsaival azonos állású kis háromszögek legyenek A típusúak, a fordított állásúak pedig B típusúak.
\(\bullet\) A szabályos háromszög felosztásánál 6 darab A típusú (felfelé mutató) és 3 darab B típusú (lefelé mutató) cella van.
\(\bullet\) Fontos megfigyelés, hogy bármely két, oldalban szomszédos cella mindig különböző típusú: az egyik A, a másik B típusú.
\(\bullet\) Legyen \(S_A\) az A típusú cellákban lévő számok összege, és \(S_B\) a B típusúaké.
\(\bullet\) Kezdeti állapot: \(S_A=0\) és \(S_B=0\).
\(\bullet\) Egy lépés hatása: Mivel mindig egy A és egy B cellát választunk, mindkét összeg vagy 1-gyel nő, vagy 1-gyel csökken, ezért az \(S_A-S_B\) állandó, így mindig 0.
Ez azt jelenti, hogy bármely elérhető állapotban \(S_A=S_B\).
A célállapot teljes összege \(S_A+S_B=2\cdot S_B\).
Válasszuk ki az \(\{n+1, n+2, \ldots, n+9\}\) halmazból azt a három elemet, amelyek a B cellákba kerülnek. Legyenek ezek \(n+i, n+j, n+k\), ahol \(i, j, k\) különböző számok 1 és 9 között. \[S_B=(n+i)+(n+j)+(n+k)=3n+(i+j+k).\] A teljes összeg a kívánt állapotban ennek kétszerese: \(2\cdot (3n+i+j+k)\) ugyanannyi, mint a teljes összeg \(9n+45\). A kapott egyenletet \(n\)-re rendezve: \[n=\dfrac{2\cdot (i+j+k)-45}{3}.\] Ahhoz, hogy \(n\) egész szám legyen, a \(2\cdot (i+j+k)-45\) kifejezésnek oszthatónak kell lennie 3-mal. Mivel 45 osztható 3-mal, \(2\cdot (i+j+k)\)-nak is oszthatónak kell lennie 3-mal. Mivel 2 és 3 relatív prímek, ez azt jelenti, hogy az \(s=i+j+k\) összegnek oszthatónak kell lennie 3-mal.
Az \(i, j, k\) három különböző szám 1-től 9-ig, összegük \(s\)
\(\bullet\) \(s\) minimuma: \(1+2+3=6\),
\(\bullet\) \(s\) maximuma: \(7+8+9=24\).
Az \(s=i+j+k\) lehetséges, 3-mal osztható értékei: 6, 9, 12, 15, 18, 21, 24. Számoljuk ki ezekből \(n=\dfrac{2\cdot (i+j+k)-45}{3}\) lehetséges értékeit.
Mivel \(n+1\) pozitív a feladat kitételei szerint, így \(n\ge 0\), tehát \(s\ge {45}/{2}\), azaz csak az \(s=24\) eset ad nekünk megfelelő megoldást, amiből következik, hogy \(n=1\).
Eddig eljutott az általam használt mesterséges intelligencia is – kicsit komplikáltabban, de eljutott –, én azonban azt mondtam neki: tulajdonképpen csak azt bizonyítottuk be, hogy \(n=1\) szükséges feltétel.
Ahelyett, hogy tüzetesen átnéznénk, hogy e feltétel elégséges-e, egyszerűbb, ha adunk egy konstrukciót (ami tehát a kilenc 0-ból 2, 3, 4, …, 10-et készít). Na, az erre tett kísérletei mind hibásak voltak, és kódot sem volt képes készíteni, ami keres egyet, vagy legalábbis olyan lassú volt, hogy én előbb készítettem egyet kézzel, papírt és ceruzát használva. Készítés közben ismét használtam a tényt, hogy a lefelé és a felfelé mutató háromszögek összege azonos. Mivel a végállapotban a teljes összeg 54, ennek fele 27 kell, hogy lefelé álló háromszögekben legyen. Az adott 10 számból 27 csak egyféleképpen állítható elő 3 szám összegeként, tehát csak a 8, 9 és a 10 lehet ebben a 3 háromszögben.
Ekkor leállítottam a keresőkódot, és megmutattam neki az ábrám fényképét, és kértem, hogy ebből csináljon normális ábrát, pontosabban egy kódot, ami a kép alapján legenerálja az ábrát. Ez 3 kísérletből sem sikerült neki. No, erre megnéztem mit csinál, két ponton kijavítottam a kódot, majd átírattam vele, hogy kézi megoldás listájából generáljon ábrákat. Az ábra nem tökéletes, de elég jó ahhoz, hogy már ne javítsam, és sokkal szebb, mint az én kézi ábráim.
Ezt a kódot használva rajzoltam 4 példamegoldást: az első, amely az első heurisztikával előállított ábrámon volt, a második ennek javított kiadása – nincs benne negatív számot használó lépés, ezáltal a létrehozó lépések száma a minimális 27. Utána készítettem még egyet, ami különböző végeredményét illetően is, majd egy utolsót, amely abban is minimális, hogy hányféle szomszéd páron végzek műveletet.
Mindegyik ábrán az élekre írt számok azt reprezentálják, hogy az él két szomszédján végeztük el a műveletet.


Megnéztem az elég jó ábrákat, és akkor jöttem rá, akárhogy írom be a maradék 6 számot, mindig található olyan lépéssorozat, hogy ezt az elrendezést létrehozzuk. Tehát összesen \(6!=720\) különböző kitöltés van, ha a forgatással, tükrözéssel egymásba vihető megoldásokat nem tekintem különbözőnek. Vajon az AI generált kód mi a csudáért nem talált meg egyet sem ebből sok perc alatt?
60. Egy síkon felvettünk 12 különböző pontot, majd pirosra festjük a pontpárokat összekötő szakaszok felezőpontját. Legkevesebb hány pontot festünk pirosra?
Válasz: 21.
Indoklás: A mesterséges intelligenciák láthatólag ismerték a feladattípust, és általam nem ismert matematikai tényekre hivatkozva állították, hogy a legjobb elrendezés ez vagy az, kettő ténylegesen az optimális elrendezést (a számtani sorozatot) ajánlotta, de belőle az egyik 21 helyett 23-at számolt.
Két út állt előttem, megkeresem (ideális esetben meg is értem) ezeket a tételeket és hivatkozom rájuk, vagy készítek egy indoklást magam. Mivel elég sok időt kaptunk a feladatokra, és tetszett a kihívás, az utóbbit választottam. Íme:
1. lépés: Miért elegendő olyan elrendezéséket vizsgálni, amikor a 12 pont egy egyenesen van?
A 12 pontot összekötő szakaszok legfeljebb 66 irányt jelölnek ki a síkon. Válasszunk egy olyan irányt, amely ezektől különböző. Ezt az irányt használva vetítsük az összes pontot egy, az erre az irányra merőleges egyenesre. Az irány garantálja, hogy a 12 pont mind különböző vetületet kap. A vetítés aránytartó (párhuzamos szelők tétele), szóval, ha két szakasz felező pontja egybe esik eredetileg, akkor a vetített párjuk felezőpontja is egybe esik, ezért a vetített 12 pont különböző felezőpontjainak száma nem lehet nagyobb, mint az eredetileg volt.
Tehát elegendő egy egyenesen lévő 12 pont eseteit vizsgálni, ha minimális számra törekszünk.
2. lépés: Miért az a legjobb, ha a pontok az egyenesen számtani sorozatot alkotnak?
Kértem a mesterséges intelligenciát, hogy magyarázza el lényeges hivatkozások nélkül, középiskolás matematikát használva. Nem tetszett a lényegében intuícióra hivatkozó magyarázata, és közben rájöttem, hogy erre a bizonyításra tulajdonképpen nincs is szükségem. Helyette bebizonyítom, hogy 21-nél nem lehet kevesebb, és a 21 előállítható a számtani sorozatos elrendezéssel.
a) A minimum 21. Van az egyenesen 12 különböző pontunk, nevezzük el ezeket rendezetten \(x_1<x_2<\ldots <x_{11}<x_{12}\). A felezőpontok akkor és csak akkor esnek egybe, ha közülük valamelyik kettő összege megegyezik másik kettő összegével.
Nézzük ezt a 11 növekedve sorakozó összeget: \(x_1+x_2\), \(x_1+x_3\), \(x_1+x_4\), …, \(x_1+x_{11}\), \(x_1+x_{12}\); és ezt a 10 növekedve rendezett összeget: \(x_2+x_{12}\), \(x_3+x_{12}\), \(x_4+x_{12}\), …, \(x_{10}+x_{12}\), \(x_{11}+x_{12}\). Vegyük észre, hogy \(x_1+x_{12}<x_2+x_{12}\), így kaptunk \(11+10=21\) garantáltan különböző összeget. Tehát az összegek, és így felezőpontok száma nem lehet kisebb, mint 21.
b) A 21 elérhető, pl. az \(x_1=0, x_2=1, \ldots ,x_{11}=10, x_{12}=11\) sorozattal.
Indoklás: Az összegek értéke egész szám, közülük a legkisebb \(0+1=1\), a legnagyobb \(10+11=21\). Tehát legfeljebb 21 különböző összeget kapunk, és az a) pont szerint van is 21 különböző összeg.
61. Ottó a hatoslottón nyolc szelvényt töltött ki, mindegyiken hat számot jelölt meg az 1, 2, …, 45 számokból. Egy számot több szelvényen is megjelölhet, de nincs két olyan szám, amelyeket együtt egynél több szelvényen is megjelöl. Legkevesebb hány különböző szám van ezen a nyolc szelvényen?
Válasz: 23.
Indoklás: A 23 elérhető. Ezt elég hamar beláttam, amikor megpróbáltam kézzel lottószelvényeket kitölteni, józan eszem használva csupán, kitöltöttem jól a 8 szelvényt mindössze 23 számmal. \((1, 2, 3, 4, 5, 6)\), \((3, 8, 13, 17, 20, 21)\), \((1, 7, 8, 9, 10, 11)\), \((4, 9, 14, 18, 20, 22)\), \((1, 12, 13, 14, 15, 16)\), \((5, 10, 15, 19, 21, 23)\), \((2, 7, 12, 17, 18, 19)\), \((6, 11, 16, 17, 22, 23)\)
Hogyan készült ez a konstrukció?
24 számra találtam konstrukciót úgy, hogy minden számot csak kétszer használtam, de próbáltam lejjebb menni. Ha van 24 számnál kevesebből álló megoldás, akkor azon kell lennie olyan számnak, amely legalább 3 szelvényen szerepel (\(6\cdot 8=48\) számot jelölünk meg, és a számokat legfeljebb kétszer használva legalább 24 szám kell). Legyen a legalább 3-szor előforduló szám az 1-es. Ezen a legalább 3 szelvényen tehát legalább \(3\cdot 5\) további számot is fel kell használnunk (az 1 ismétlődése akadályozza, hogy bármely számot egy másik szelvényen újra felhasználjunk), tehát beláttuk, hogy 16 számnál kevesebb biztosan nem elég.
Ki van töltve 3 szelvény. Hogyan tovább? A \(3\cdot 5\) már használt számot most mind különbözőre tesszük. Igazából nem látszik nyilvánvalóan más (közel) optimális megoldás. Marad az 5 szelvényen további 3-3 kitöltendő. Ez lényegében 5 szelvény hármas lottón való kitöltése új számokkal, mert a régiek már mind konfliktusban lennének. Ha legfeljebb 7 újabb számot szeretnénk használni, akkor \(2\cdot 7<15\) miatt legalább az egyik számot megint háromszor kell használni, legyen ez a 17. Ehhez viszont legalább \(3\cdot 2=6\) új szám kell. Szerencsére a kimaradó 6 helyre ezt a 6 számot újból fel tudtam használni. Szóval kaptam megoldást 23 számmal. Öröm, de van-e kevesebb?
Úgy éreztem, hogy akárhogyan próbálom másképp, nem lesz jobb a helyzet. Pl. ha 4 szelvényen 1-essel indulok, akkor ahhoz rögtön 20 további szám kell – együtt már 21, és a maradék kitöltése nem oldható meg egyetlen új szám bevezetésével. De nem hagyott nyugodni, hátha van jobb megoldás. Hogy 22-nél kevesebb szám nem elég, azt lényegében beláttam, de akárhogy erőlködtem, nem tudtam 22 számmal megoldást találni.
Öt mesterséges intelligenciával is hosszas beszélgetésbe kezdtem a feladatról. Előjött a Steiner-rendszer, a Fano-ábra – ezeknek némileg utána is olvastam, mert hihetően hangzott, hogy jó kiindulás lehet a feladathoz, még nézegettem is ezzel kapcsolatos hasonló matematikai problémákat. Három AI arról győzködött, hogy 16 szám elég, a negyedik pedig 48-t mondott megoldásnak (a 45 számos lottón, haha), na vele le is zártam a témát. Az ötödik hosszas gondolkodás után feladta a megoldás keresését. Én már tudtam, hogy 16 nem jó, de kíváncsi voltam, mi lesz, ha szembesítem „őket” hibáikkal.
Egyiküknek annyira tetszett a teljes konstrukcióm, hogy meg akart győzni, megvagyunk a feladattal, semmi ötlet nem támadt a vele való beszélgetésből a továbbiakban.
Ebből tanulva a másiknak csak annyit mondtam, hogy hallucinál, a 16 nem jó, be is tudom bizonyítani. Na, erre „mélyen magába nézett”, és valamilyen Fisher-egyenlőtlenségre és Wilson-féle létezési tételre hivatkozva azt mondta, hogy 31 szám kell, és arra van is megoldás.
Mondom neki: „Ez sem igaz, mivel van már 23 számból álló korrekt megoldásom. Csak arra vagyok kíváncsi, hogy lehet-e 22. Annál kevesebbel már bebizonyítottam, hogy nem lehet megoldást konstruálni” – kicsit túloztam, a 22-es bizonyítást is szőrözni kellett volna még.
Ekkor megtörtént a csoda, két merőben rossz válasz után előállt egy elegáns bizonyítással, hogy miért 23 a minimum. Ez nekem elsőre nehéz (túl tömény) olvasmány volt, így megkértem egy másik mesterséges intelligenciát, segítsen értelmezni a lépéseket.
Íme ennek az átírásnak az eredménye (némi kézi módosítással):
Az alsó korlát bizonyítása
A cél annak bizonyítása, hogy a feladat feltételei mellett legalább 23 különböző számra van szükség.
1. Változók definiálása
Legyen \(v\) a felhasznált különböző számok száma. Legyen \(r_{i}\) az \(i\)-edik szám előfordulásainak száma a 8 szelvényen (ahol \(i\) 1-től \(v\)-ig fut). Mivel 8 szelvényen 6-6 szám van, a számok összes előfordulása: \[\displaystyle\sum^v_{i=1}{r_i}=8\cdot 6=48.\]
2. A négyzetek összegének becslése
Tekintsük a \(\displaystyle\sum r_{i}^{2}\) összeget. Felhasználjuk a következő azonosságot: \(r^2=r+\dfrac{2r(r-1)}{1\cdot 2}=r+2\dbinom{r}{2}\). Ezt összegezve minden \(i\)-re: \[\displaystyle\sum^v_{i=1}{r^2_i}=\displaystyle\sum^v_{i=1}{r_i}+2\displaystyle\sum^v_{i=1}{\dbinom{r_i}{2}}.\] A \(\displaystyle\sum^v_{i=1}\dbinom{r_i}{2}\) tag a közös számokon osztozó szelvény-párok teljes számát jelenti. Az összes lehetséges szelvény-pár száma \(\dbinom{8}{2}=28\). Ebből adódik a becslés, hogy \(\displaystyle\sum^v_{i=1}{\dbinom{r_i}{2}}\le28\). Behelyettesítve: \[\displaystyle\sum^v_{i=1}{r^2_i}\le 48+2\cdot 28=104.\]
3. A Cauchy–Bunyakovszkij–Schwarz-egyenlőtlenség alkalmazása
\(\left(\displaystyle\sum^n_{i=1}{x_iy_i}\right)^2\le \left(\displaystyle\sum^n_{i=1}{x^2_i}\right)\left(\displaystyle\sum^n_{i=1}{y^2_i}\right)\). Legyen \(x_{i}=1\) és \(y_{i}=r_{i}\).
Ekkor \[\left(\displaystyle\sum^v_{i=1}{r_i}\right)^2\le \left(\displaystyle\sum^v_{i=1}{1^2}\right)\left(\displaystyle\sum^v_{i=1}{r^2_i}\right),\] azaz \[\left(\displaystyle\sum{r_i}\right)^2\le v\cdot \left(\displaystyle\sum{r^2_i}\right).\] Behelyettesítjük az ismert értékeket és a kapott becslést: \[48^2\le v\cdot 104.\] Átrendezve: \[2304\le 104v.\]
4. Konklúzió
Az egyenlőtlenséget \(v\)-re rendezve kapjuk: \[v\ge \dfrac{2304}{104}\approx 22{,}15.\] Mivel \(v\) egész szám, ebből következik, hogy \(v\ge23\). Mivel létezik konstrukció 23 számra, ez a minimális érték.
62. A LogikuSakk Egyesület edzőtábort szervez 16 sakkozójának, ahol minden játékosra 3 mérkőzés vár, és ezt a beosztást, hogy ki kivel fog játszani, már elkészítették. Igaz-e, hogy az előírt edzőmérkőzések lebonyolíthatók 3 nap alatt úgy, hogy senki sem játszik 1-nél több mérkőzést naponta?
Válasz: nem igaz.
Indoklás: Sokszor el kellett olvasnom a feladatot, mire megértettem. A beosztás számomra azonos a napokra osztással, hogy a feladatnak értelme legyen, a beosztás csak azt tartalmazza, hogy ki melyik 3 másikkal kell, hogy megmérkőzzön, ezt valaki már kőbe véste, most azt kell megnéznünk, hogy ez minden esetben lebonyolítható-e 3 nap alatt.
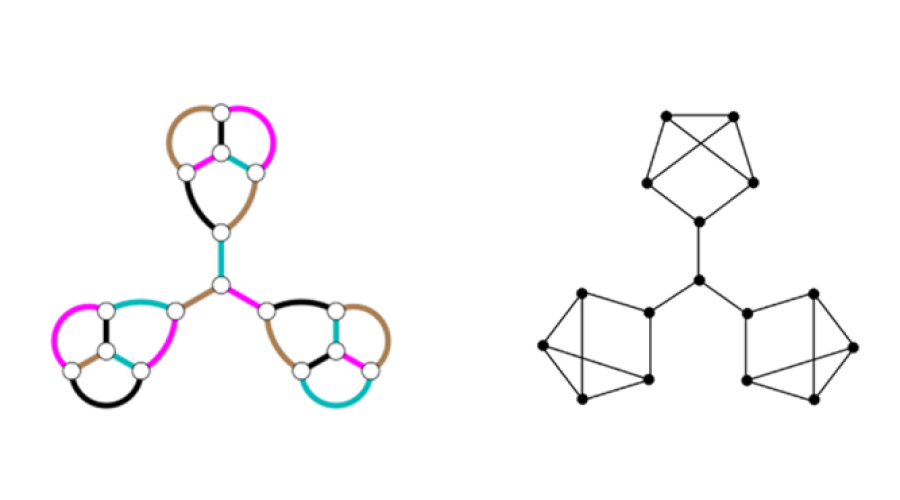
Fogalmazzuk át a feladatot a gráfok nyelvére. A gráf csúcsai a játékosok, az élek pedig a mérkőzések. Minden csúcsból 3 él indul. Színezzük ki az éleket aszerint, hogy melyik nap játszák az adott mérkőzést. Ha a színezéshez mindig elég 3 szín, akkor a feladat állítása igaz.
Elkezdtem színezgetni kis gráfokat, és már 5 csúcspontnál gondokat láttam, igaz ekkor az egyik csúcspont még csak két éllel rendelkezik. Rendben, kössünk össze 3 ilyen készletet 1 összekötő ponttal, ez összesen 16 pont, s rögtön van példánk arra, hogy legalább 3 mérkőzésnek is egy negyedik napra kell kerülnie.
Készítettem egy vázlatot, amit mesterséges intelligencia segítségével szépítettem. Egy arcot szerettem volna rajzolni. Nehezebben ment, mint vártam, de a végén csak összejött elfogadhatóra, íme:

A szimmetria megsértése nélkül feltehetjük, hogy a 0, 1, 2 csúcsok közötti éleket az ábra szerint beszínezzük pirosra, zöldre és kékre, ekkor a \((0,3)\) és a \((2,3)\) élek színe adódik. A 13-as csúcsba az 1 és a 3 csúcsokból is kékkel kéne indulni, ami miatt az egyiknél egy negyedik színt kell alkalmaznunk. Ez az 5 pontos alap, amiről írtam. A 12-es pont, ami összeköti a három, külön-külön is problémás alakzatot.
Persze megkérdeztem a mesterséges intelligenciát is. Elmondta, hogy ezt a feladatot egy 19. századi dán matematikus, Julius Petersen már megoldotta.
63. A tér minden egyes pontja öt szín egyikével van színezve, és a színezéshez mindegyik színt felhasználtuk. Igaz-e, hogy mindig van olyan sík, amelyen legalább 4 szín szerepel?
Válasz: igaz.
Indoklás: Sokáig hittem, hogy nem igaz, és tudok ellenpéldát konstruálni. Az egyik mesterséges intelligencia is arról győzködött, hogy a csavart köbös görbe kiváló ellenpélda. Ez a görbe gyönyörű, sok időt töltöttem vele, míg megértettem, de sajnos nem ellenpélda.
Végül a sok beszélgetés formálta a gondolataimat a feladatról, és beugrott egy konstruktív kereső algoritmus: adj nekem egy pontosan 5 színnel kiszínezett teret, és meg tudom mondani, hogyan találj benne olyan síkot, amiben legalább 4 szín van.
Az alapötlet egy gondolat ismételt alkalmazása: ha egy bizonyos konstrukció nem vezet eredményre, akkor arról a konstrukcióról többet tudok, és a többletet felhasználva újabb lehetséges síkokat jelölök ki. A legvégén pedig két olyan állapothoz jutok, ami közül az egyik biztos megoldás.
Legyen az 5 szín \(A\), \(B\), \(C\), \(D\), \(E\).
Válasszunk ki a térből öt pontot, \(P_A\), \(P_B\), \(P_C\), \(P_D\), \(P_E\) jelöléssel, egyet-egyet mind az öt különböző színből. Mivel mind az öt színt használtuk, ilyennek kell lennie. Ha e pontok közül bármelyik négy egy síkba esik, akkor megtaláltuk a keresett négyszínű síkot.
Ha nem, a keresést folytatjuk. Ebben az esetben a \(P_A\), \(P_B\), \(P_C\), \(P_D\) pontok egy tetraéder csúcsait alkotják.
Vizsgáljuk meg a tetraéder lapjait, például a \(P_A\), \(P_B\), \(P_C\) pontok által alkotott \(S_{ABC}\) síkot. Ha ez a sík tartalmaz a csúcsok színein kívül egy negyedik színt is (pl. \(D\) vagy \(E\)), akkor megtaláltuk a keresett síkot.
Ha nem találunk ilyen síkot, az azt jelenti, hogy a tetraéder minden lapja kizárólag a három csúcsának megfelelő színt tartalmazza. Például az \(S_{ABC}\) síkon csak \(A\), \(B\) és \(C\) színű pontok vannak.
Most vizsgáljuk a tetraéder éleit, például a \(P_A\) és \(P_B\) pontot összekötő \(e_{AB}\) egyenest.
Ez az egyenes teljes egészében benne fekszik az \(S_{ABC}\) síkban. Az előző lépésben megállapítottuk, hogy ezen a síkon csak \(A\), \(B\) és \(C\) színű pontok lehetnek. Ebből következik, hogy ha az \(e_{AB}\) egyenes a két végpontján kívül tartalmaz más színű pontot, annak a pontnak szükségszerűen \(C\) színűnek kell lennie.
Hasonlóan az összes élre, ha valamelyik élegyenes 3-színű, akkor ez az egyenes és \(P_E\) pont egy 4-színű síkot feszít ki.
Most már csak azt az esetet kell vizsgálnunk, amikor a tetraéderünk bármely élének egyenese pontosan 2-színű (az a kettő csúcs színe, ami az élt meghatározza).
Vegyük a tetraéder két kitérő élét, például az \(e_{AB}\) és \(e_{CD}\) egyeneseket és \(S_{ABE}\), valamint az \(S_{CDE}\) síkokat (a \(P_A\), \(P_B\), \(P_E\) pontok és a \(P_C\), \(P_D\), \(P_E\) pontok síkjait). Az \(S_{ABE}\) és az \(S_{CDE}\) síkok metszik egymás, hiszen van közös pontjuk (a \(P_E\)), és van nem közös pontjuk is (a kitérő egyenesek pontja). Legyen ez a metszésvonal \(m\).
Ha az \(e_{CD}\) egyenes nem metszi az \(S_{ABE}\) síkot, akkor az \(e_{CD}\) egyenes párhuzamos \(m\)-mel, hasonló állítás igaz, ha az \(e_{AB}\) egyenes nem metszi az \(S_{CDE}\) síkot, az \(e_{AB}\) egyenes párhuzamos \(m\)-mel. De az \(m\) egyenes legfeljebb a két kitérő egyenes egyikével lehet párhuzamos.
Legalább az egyik metszés megvalósul, és az egy negyedik színt visz be az adott háromszínű síkba. (Az 1. esetben az \(S_{ABE}\) síkba kerül egy \(C\) vagy \(D\) színű pont, a 2. esetben pedig az \(S_{CDE}\) síkba egy \(A\) vagy \(B\) színű pont.)
Mindkét esetben megtaláltuk a legalább négyszínű síkot.
Az eljárás minden lehetséges kimenetele egy legalább négyszínű sík felfedezéséhez vezetett.
Turchányi Gyula