1. Bevezetés
Világunk térbeli törvényszerűségeinek megismerése, továbbá megfogalmazása kapcsolatot hoz létre a matematika és a minket körülvevő művészet között, a logikai, valamint az esztétikai szépség együttes megjelenítésével. Az ezzel foglalkozó geometria viszont olyan mély gondolatokat rejt magában, amelyekről az emberek túlnyomó hányadának nincs is és nem is lehet ismerete. E teóriákból felvillantva néhányat, eljutunk egy olyan − számítógéppel megvalósítható − világba, amelyben figyelemre méltó alkotások találhatók, illetve hozhatók létre.
Először is ismerjük meg azt a három matematikust, akik sokat tettek a matematika két ága, a topológia és a geometria területén. (Ismeretes, hogy a topológia az alakzatok olyan tulajdonságaival foglalkozik, melyek folytonos − vagyis szétszakítás és összeragasztás nélküli − leképezések során változatlanok maradnak.)

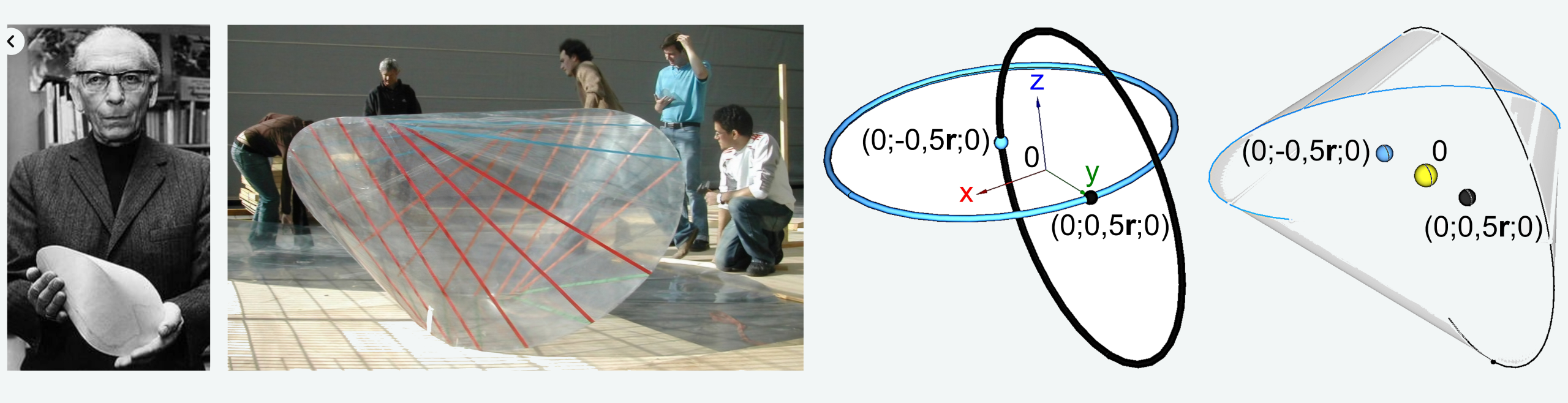
Topológiában a vizsgált csomóknak nincsenek végeik, zártak. (A csomó tulajdonképpen egy síkbeli kör 3 dimenziós térben való elhelyezése.) Az ilyen tárgyú szakmunkákban általában vizsgált csomókat és láncokat az [1] és [2] tanulmány látványosan jeleníti meg, mintegy hidat képezve a művészi szépség felé. Az [1] cikkből vettük át a két alkotógörbéjű Seifert-felület rajzát az 1.1. ábrán. Az említett felület határa a feltüntetett Hopf-lánc. (Ezen orientált felület átlagos görbülete zérus, lokálisan a területe a legkisebb.) A következőkben leírtak egyik inspiráló forrása ez a felület volt. A másik kiindulópont, egy olyan szemrevaló – és figyelemre méltó tulajdonságokkal bíró – alakzat, ami egyszerűsége ellenére számos gondolatot indukált. A sokoldalú Paul Schatz által felfedezett oloid testet (egyszeres) vonalfelület határolja. (Vonalfelület az, amelynek minden pontjára illeszthető olyan szakasz, amelynek pontjai a felületre illeszkednek.)
Az oloidhoz elvezető alapgondolat ez volt: egy kocka három részre felbontható úgy, hogy az elemek rugalmas csatlakoztatásával egy teljesen kifordítható lánc jön létre. A testláncnak három egyenlő és állandó hosszúságú átlója van az ellentétes csuklók (ízületek) között, amelyek az eredeti kocka térbeli átlói. Schatz megfigyelte azt az utat, amit egy ilyen átló megtesz (végigsöpör), ahogyan a testlánc kifordul, és rájött erre az egyszerűen nagyszerű testformára. A „kifordítható” kocka (invertible cube) ötletét általánosítva azután a további négy szabályos (platoni) poliédernek is megalkották a „kifordítható” alakzatát.
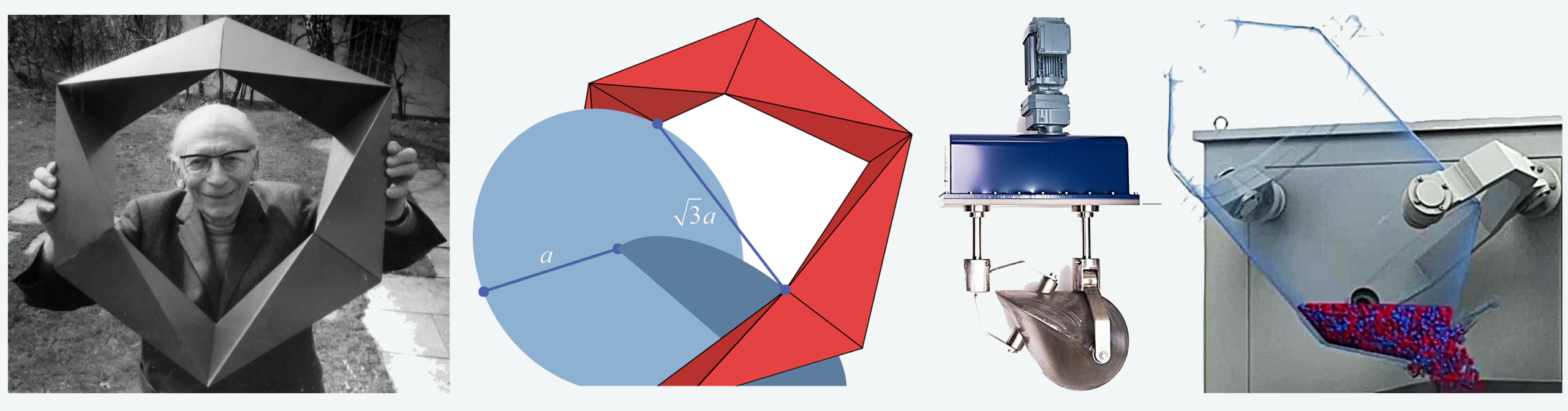
Az oloid test síkon való „tántorgóan” gördülő mozgásának mélyreható elemzése, egy olyan térbeli 6-rudas, forgócsuklós mechanizmus megalkotását is elősegítette, amelynél a középső tag „oloid-mozgású”. Ez utóbbi azt jelenti, hogy a meghajtott mechanizmus ezen rúdjának mozgásakor, annak minden pontjára, a tér minden irányát bejáró tehetetlenségi erő hat. Ha ez a mechanizmustag egy áramoltató elem vagy anyagtartály, akkor létrehozhatunk egy kiválóan működő hullámgenerátort, vagy egy keverőegységet.
2. Egy új geometriai alakzat lehetősége és létrehozása
Az alapötlet a következő: az oloid származtatását kiterjesztve, a két merőleges síkú alkotókör közepeit excentrikusan toljuk el síkjaikban egy bizonyos mértékben. A koordináta-rendszer két nem ugyanazon síkjához képest a körközéppontok lehetnek a sugaruk egy hányadának megfelelő távolságra is, pl. ahogy a 2.1. ábra baloldala mutatja. A két alkotó-görbe által meghatározott és abból megszerkeszthető vonalfelületet − önkényesen − nevezzük el duploidnak.

(A duploid és az alakzat körsíkjai a koordináta-rendszer síkjai, továbbá \(e= r/\psi\) \((\psi>1)\) távolság az excentricitás.)
A hármas (Borromean) lánc ötletéből kiindulva, alkalmasan megválasztott elhelyezésű 3 alkotókör (lásd a 2.1. ábra jobboldalát), meghatározhat egy eddig még nem ismert – és a \(\psi=r/e\) aránytól függő formájú – alakzatot. (A köregyenletek: \((x+e)^2+(y-e)^2=\psi^2e^2\), \(z=0\); \((x-e)^2+(z+e)^2=\psi^2e^2\), \(y=0\); \((y+e)^2+(z-e)^2=\psi^2e^2,\) \(x=0\).)
Az \(r/\psi=e\) excentricitású duploid (lásd 2.2. ábra) megrajzolásához meg kell választani a \(\psi\) excentricitási arány értékét. Többfélét kipróbálva, végül a \(\psi=10^{0,5}\) arányszám tűnt célszerűnek. (Ez esetben, a koordinátasíkbeli alkotókörök az origótól vett \(2e\) távolságban metszik egymás síkját, lásd az alábbi ábrán feltüntetett zöld, mályva és kék színű pontokat!)
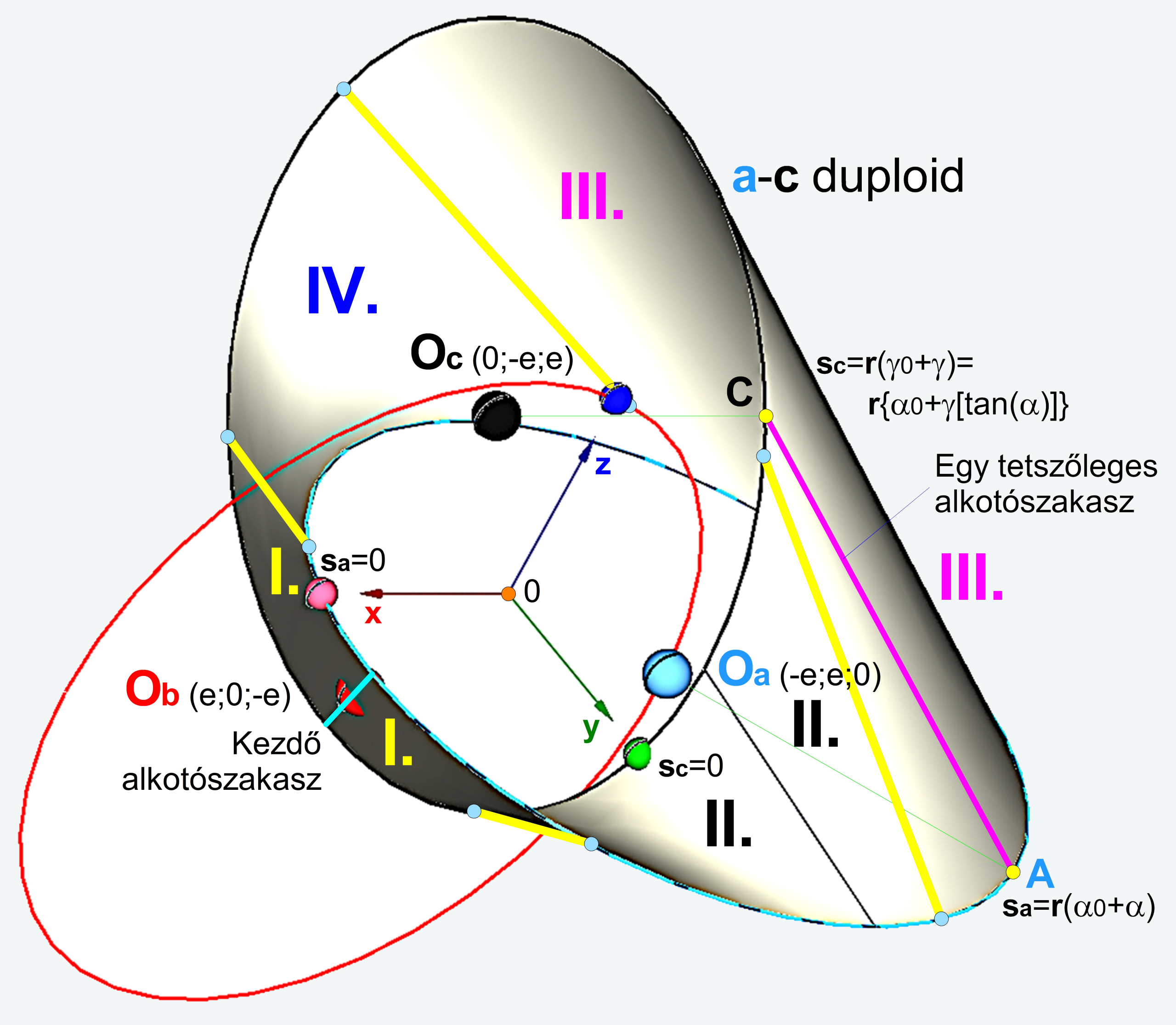
[Duploid résztartományai: I. (konkáv felületrész), II. (innenső felületátmenet), III. (konvex felületrész), IV. (túloldali felületátmenet), valamint \(s_a\), \(s_c\) a leíró ívhossz-koordináták.]
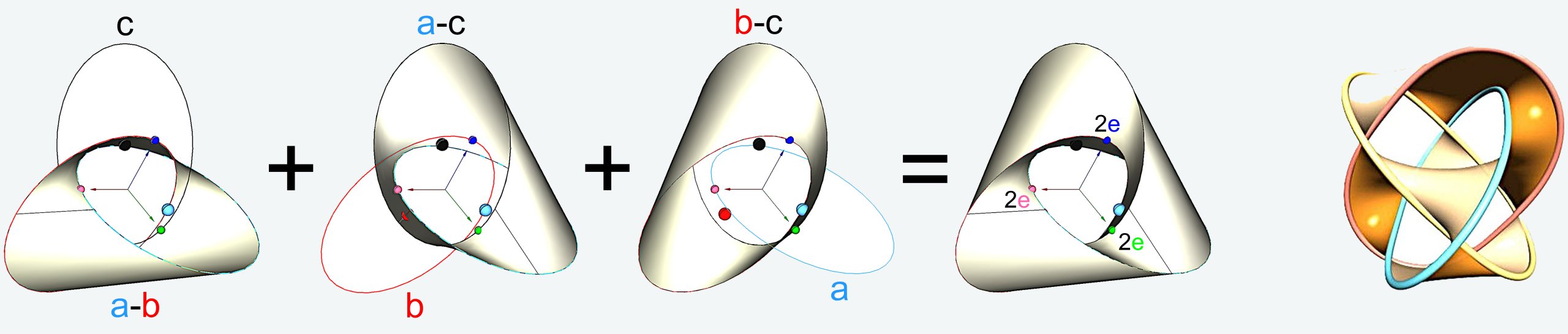
(az „anti-” névelőtag a „lyukasságot” jelenti, ez fejezi ki az előzetes várakozással ellentétes – nem várt – formát, ami topológiailag azt is jelenti, hogy az ilyen alakzat a tórusszal homeomorf, nem pedig a gömbbel).
A kívánt 3-alkotógörbés alakzat duploidjai egy lyukas testet alkotnak. Láthatjuk a 2.3. ábrán azt is, hogy a kapott három vonalfelület együttese mennyire más, mint a Seifert-féle minimálfelület [1]. (Az előállt anti-trioid test tulajdonképpen az oloid egyfajta általánosítása.)
A duploid származtatási módjai:
- Érintőmódszer (itt az alkotószakasz végpontjaihoz illesztett körérintők a hozzátartozó koordinátatengelyen metszik egymást) alkalmazása a [3] szakirodalom alapján.
- Kinematikai metódus, itt két geometriai pontot indítunk útnak adott \(A\), illetve \(C\) kezdőpozícióval megadott érintési helyekről és egyenletes sebességet, valamint azonos befutási időt tételezzünk fel. Ekkor a két mozgó pontot összekötő – változó hosszúságú – vonalszakasz végigsöpör egy felületet.
- CAD-programokban alkalmazott pásztázási mód/parancs (loft-method).
A külpontossági tulajdonság miatt lett az ilyen és hasonló alakzatok összességének elnevezése excentoidok.
3. Az új alakzatcsalád áttekintő bemutatása
Az excentoidok kijelölő alkotógörbéi zárt görbék (a matematikai csomókéhoz hasonlóan, ugyanis, ha nyitottak lennének, akkor megjelennének egyenes lezáró élek). Nem feltétel, hogy a görbék síkjai egymásra merőlegesek legyenek. Excentricitási arányuk jellemzően \(\psi=10^{0,5}\) (ha ettől eltérő, akkor az külön jelölöm, pl. nagyon „lyukas” anti-trioidnál, \(\psi\) is nagy értékű). A térben tervezetten konfigurálva vannak elhelyezve, a jellemző szimmetriasíkokhoz képest eltolt középponttal, különféle sík-szögállással.
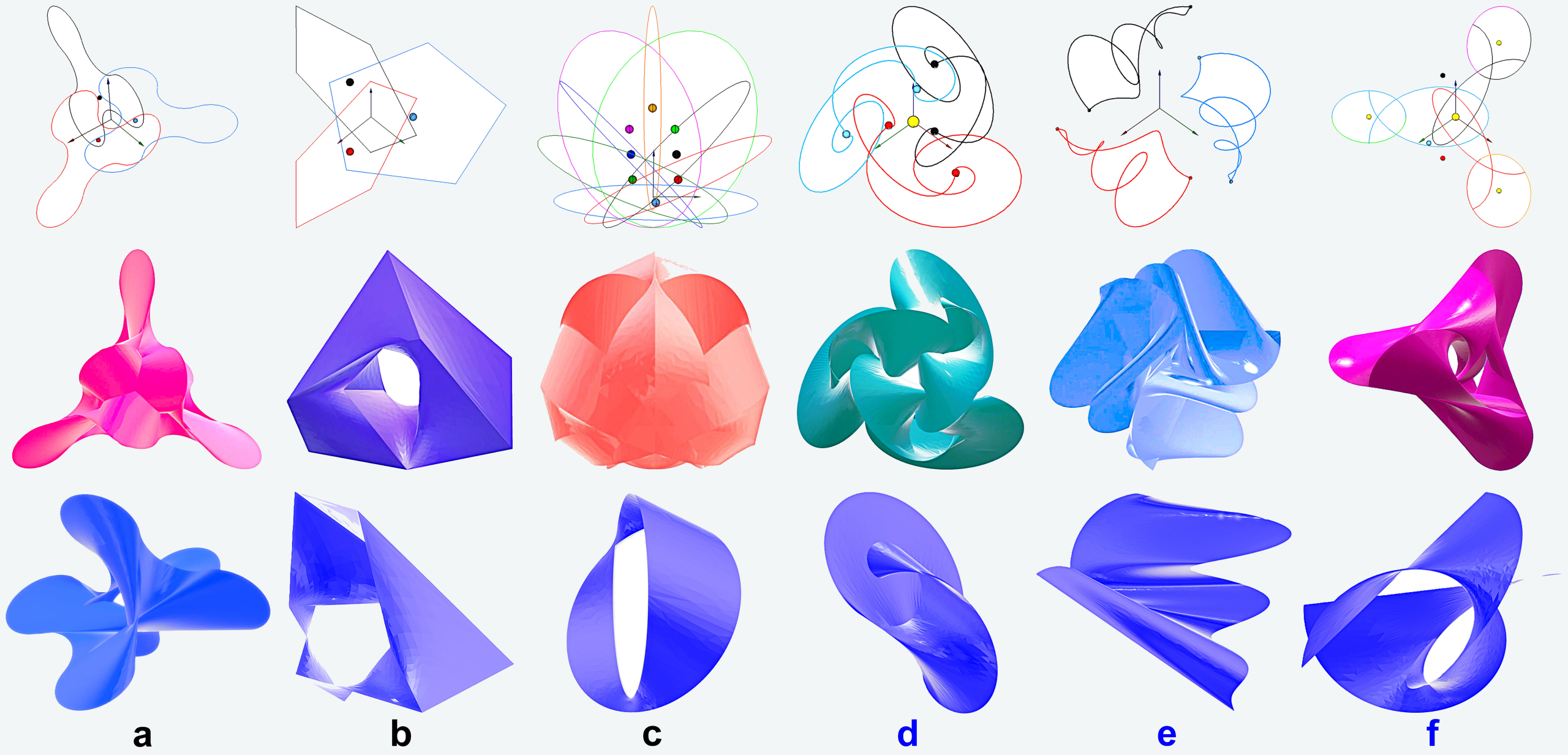
A több mint 150 különféle alakzat léte már megkövetelte az informáló sorszámozást. Síkbeli alkotógörbéjű excentoidoknál az első (piros) szám a kijelölő görbék számát jelenti (1.-től 9.-ig). Térbelieknél 1000 fölött kezdődik a számozás, mégpedig 10: Spiraloidok, 11: Helixoidok, 12: Curvoidok, végül 13: Hibridek.

A mutatós alkotófelületekből igen sok van, ezek számozása csak a hozzátartozó excentoidra utal.
4. Excentoidok világa
Alkalmazott alkotógörbék:
- síkbelieknél – kör, ellipszis, tojásgörbe, többféle egyedi szerkesztett mérnöki görbe;
- térbelieknél – kör, körív, arkhimédeszi spirál, hélix és (kétféle módon is kúpos) hélix görbékből összetett görbepárok.
Nem kötelező az azonos méretű alkotógörbék alkalmazása.
4.1. Síkban fekvő alkotógörbékből származtatott alakzatok (2D-görbékből születő 3D-alakzatok)
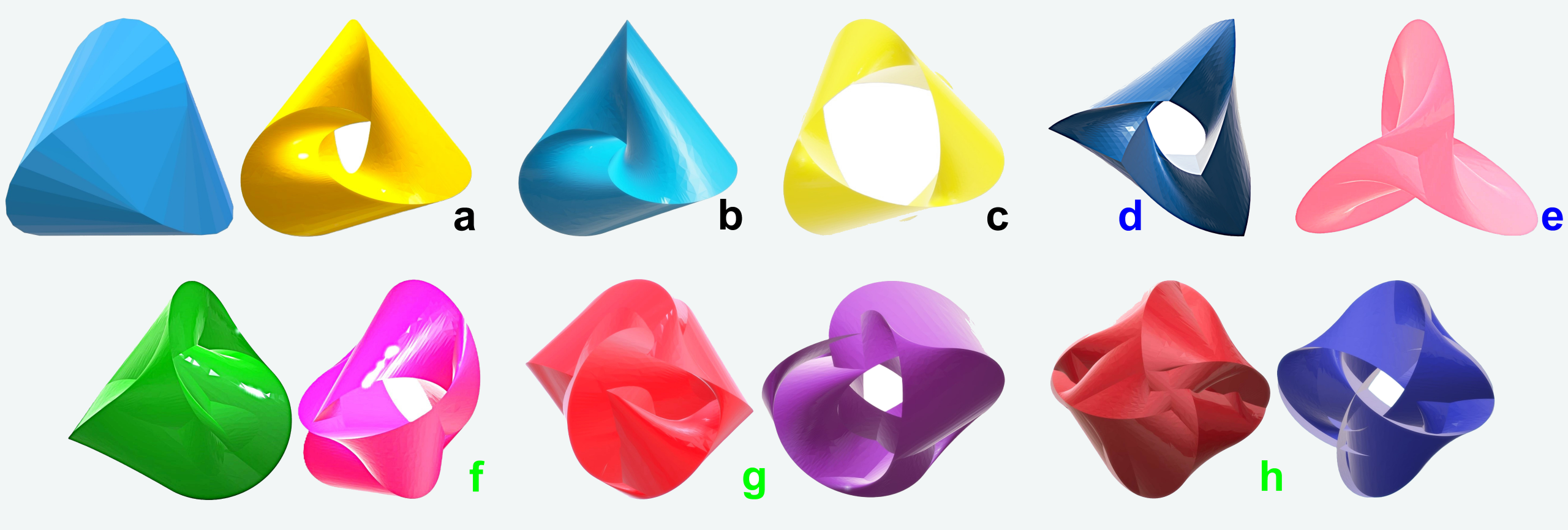
Egy-egy excentoidnál a választott alkotógörbe konfiguráció már mutatja azt, hogy van-e esély „szemrevaló” alakzat megalkotására, vagy sem. Sok görbénél alkalmazható az aranymetszés arányszáma, a \(\varphi=0,5(1+5^{0,5})=1{,}61803\) érték, épp a harmonikus megjelenés előállítása miatt.


4.2. Térbeli alkotógörbékből származtatott alakzatok (3D-görbékből alkotott 3D-alakzatok)
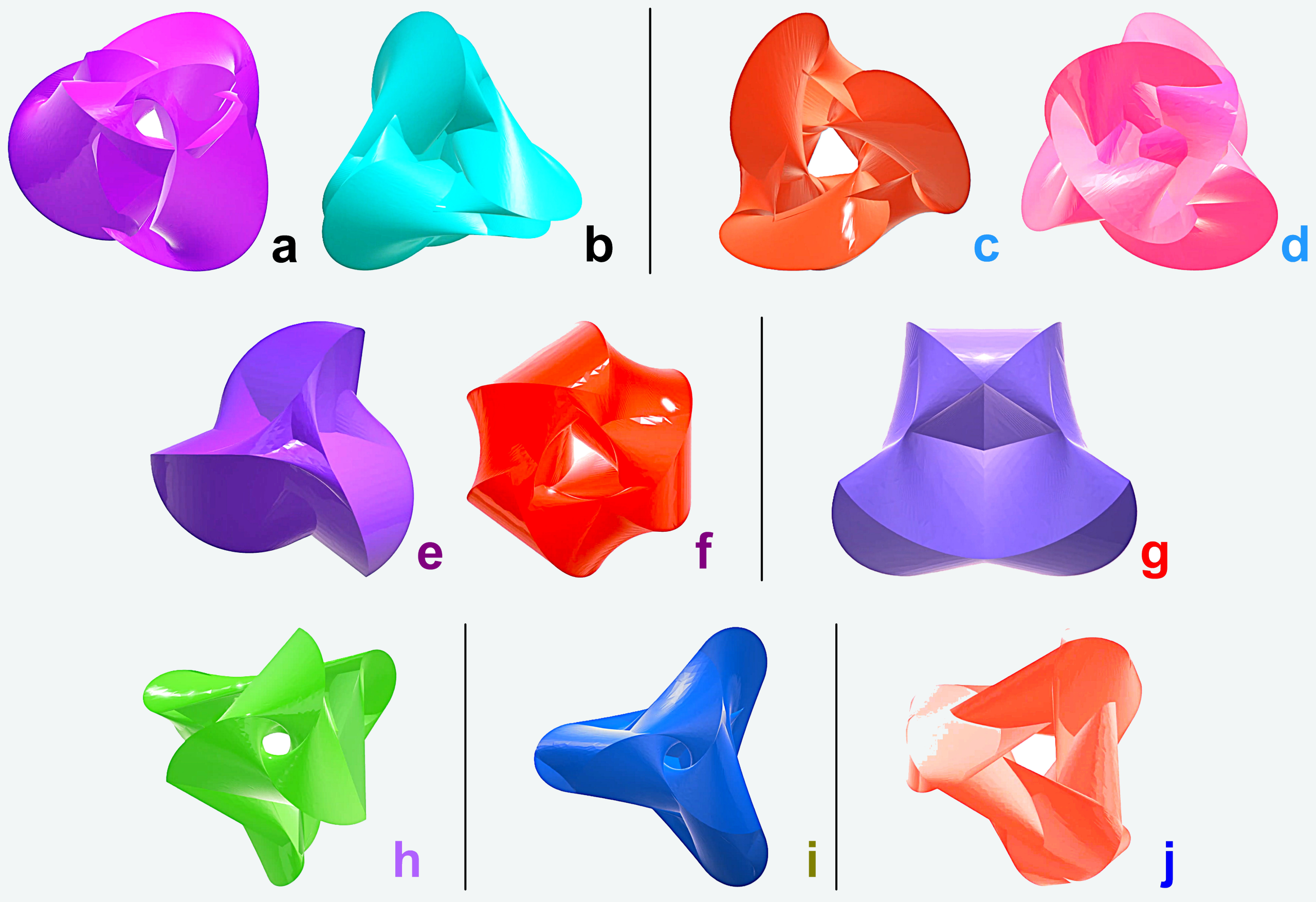
Jellemzően egymásra merőleges síkú kijelölő görbepárok alkotják a térbeli görbéket. A görbepár-tagok körök, körívek, arkhimédeszi spirálok, hélixek, (csonka)kúphélixek és kúphélixek lehetnek. A hibridek alkotó görbepár-tagjai nem azonos geometriájúak.
Az alkotógörbe-tagok középpontjai: helixoidoknál, egy-egy hélix (indító) alapkörének középpontja; spiraloidoknál, egy-egy spirál kezdőpontja; curvoidoknál, a körívek középpontjai.
Az excentricitási arányok ugyanazok: helixoidoknál, az alapkörsugárt véve, \(\psi=r/e=10^{0,5}\); spiraloidoknál, a spirálpár-
A térbeli konfigurációs lehetőségek rendkívül sokfélék, akár a síkbeli alkotógörbés alakzatoknál.
5. Alkalmazási lehetőségek
Az excentricitással eltolt alkotógörbe-középpontú alakzatok (felületek és testek) meglepően nagy formagazdasága (az esztétikustól a bizarrig) sokféle használati irányt jelöl ki. Vegyük ezeket sorra.
- Szereléstechnológiai tesztelésekhez célszerűen kiképzett mintaalkatrészek. Az ipari robotokat alkalmazó automata rendszereknél fontos a megbízható és konfigurálható (és gépi látással segített) robotmegfogó alkalmazása. Ez legjobban az igazodó (compliant) „ujjvégződésű”, és az „ujjaikat” szükség szerint átcserélő, automata eszközökkel érhető el. (Valójában, ez a fejlesztési feladat ösztönözte a nehezen manipulálható, görbült alkatrészformák keresését a megfogási próbákhoz!)
- Absztrakt vagy kinetikus szobrászat világa: például, térbeli giroszkóp-szerű szobrok, illetve fény- és vízjátékok, bel- és kültéri statikus vagy dinamikus installációk.

- Olyan új térbeli mechanizmusláncok (pl. 2, 3 vagy több forgó- és gömbcsuklóval rendelkező, rudas mechanizmusok összekapcsolásával) felfedezése, melyek gömbcsuklós végű csatlórúdjai teleszkóp kialakításúak (golyós csavarorsósak), a hosszúságuk változtathatósága végett. Ha ezt szabályozni akarjuk, akkor elektromechanikus működtetővel („slave servo drive”) megtehetjük.
- Parametrikus építészeti térformák szisztematikus keresése (koncepció-katalógusban való összeállítása, külön jelölve a homorú felületrészekkel járó alkalmazási veszélyeket), elkerülve a Bézier-görbés megoldásokat, amelyeket csak a leggazdagabb megrendelők engedhetnek meg maguknak, a drága technológiai megoldási igény, illetve a legyártás nehézségei miatt.
- Ékszerek tervezése. (Például: a születési dátumot geometriailag kódoló amulettek additív gyártása.)

- Lámpaernyők, művészi használati tárgyak (például: fraktál ornamentikájú felülettel vagy áttört neuron-hálós mintázatú palásttal), 3D-s céglogók, formatervezett dizájn- és reklámtárgyak.
6. További kutatási és fejlesztési irányok
- Egy-egy kiemelkedően attraktív, de nem túlságosan összetett konfigurációjú, kevésbé bonyolult geometriájú excentoid alakzat matematikai leírása algoritmussal.
- Egy-egy egyszerűbb konfigurációjú excentoid algoritmusos 4-dimenziós modelljének megalkotása (már ismert 2D-s vagy 3D-s függvényekből), amelynek 3-dimenziós nézetei újabb ígéretesen látványos alakzatokat generálhatnak.
- Az előbb említett alakzatok jellemzését szolgáló „skeleton”-ok [középtengely-transzformációs „csontvázak” (medial axis transform)] megállapítása.
- Minőségi 3D-s nyomtatást elősegítő – pl. adaptív Delaunay-sokszögű – felületi hálók kidolgozása (STL (Standard Triangle Language) helyett). Ez különösen a „megcsavart” felület-átmeneteknél problémás, ha a technológiai gyárthatóságot nézzük (vizsgálva e palástrészek kiteríthetőségét).
Az ábrákon bemutatott excentoidokhoz (illetve még annál jóval több alakzathoz) készültek − a származtatást bemutató és a térbeli geometriát megjelenítő – animációk. Ezek a nem túl távoli jövőben mindenki számára elérhetők lesznek. Mert ezt az inspirálóan különleges geometriai világot sokak számára ismertté tenni – hitem szerint – érdemes.
Zsák Zoltán gépészmérnök
Irodalom
[1] Jarke J. van Wijk and Arjeh M. Cohen. Visualization of Seifert Surfaces. Technische Universiteit Eindhoven, 2006.
[2] Mathias Carlen. Computation and visualization of ideal knot shapes. 2010.
[3] Hans Dirnböck and Hellmuth Stachel. The Development of the Oloid. Institute of Mathematics, University Klagenfurt – Institute of Geometry, Vienna University of Technology, 1997.