Egy klasszikus csomóelméleti kérdés megoldása

Bár a csomók − önmagukba záródó, és magukat nem metsző hurkok a háromdimenziós térben, amelyeket mozgatni-nyújtani-zsugorítani szabad, de elvágni és ragasztani nem − matematikai elmélete csak a 19. század vége felé körvonalazódott, számos előkép és legenda előzte azt meg. Használták a kultúrák hajnalán törzsek jelölésére, állítólag a legegyszerűbb (nemtriviális) csomó még Thor kalapácsán is megjelent.

De a történelem leghíresebb csomója azért a nevezetes gordiuszi csomó marad. A legenda szerint a Gordion városában található csomót (amely Gordiosz későbbi király – Midász király apja – szekerének jármát rögzítette a rúdhoz) kell annak kicsomózni, aki Ázsiát (vagy Kis-Ázsiát, ez nem volt világos) akarja meghódítani. A kicsomózást nehezítette, hogy a csomó két vége a csomó belsejébe lett elrejtve (tehát itt nem a matematikai értelemben vett csomó fogalmáról volt szó).

Ismét a legenda szerint Nagy Sándor ázsiai hadjárata alkalmával, miután rövid ideig nézegette a csomót, kardjával egyszerűen kettévágta, megteremtve a nehezen megoldható problémák könnyed, nem konvencionális megoldásának archetípusát. A történeti hűséghez hozzátartozik, hogy ugyan a csomót nem a szabályoknak megfelelően csomózta ki, de Ázsiát (legalábbis az akkor ismert terület jelentős részét) meghódította.

Ezen túl azonban ötletet is adott arra, hogyan lenne érdemes csomók bonyolultságát mérni. Egy matematikus számára két csomó akkor ugyanolyan, ha egyik a másikba alakítható anélkül, hogy elvágnánk, majd később a szabad végeket újra összeragasztanánk. (Az olyan csomók, amelyek egy szakaszon, vagy köznapibb helyzetben, egy cipőfűzőn keletkeznek, mindig kicsomózhatók, ilyenkor a kicsomózásnak pusztán türelmünk szabhat határt.) A matematikai csomók kicsomózásának egy elemi lépése a következő: vetítsük le a csomót a síkra. A gyakorlatban ezt úgy képzelhetjük el, hogy a kötélből készített csomónkat (amelynek tehát nincs vége, a kötelünk két végét a csomózás után gondosan összeforrasztottuk) ejtsük le a földre. Általában így a vetületben keletkeznek olyan pontok, ahol a csomónak két szála is átmegy, az egyik alul, a másik felül. (Egy általános vetületben nem lesznek például háromszoros vagy négyszeres pontok, a továbbiakban mindig feltesszük, hogy a vetületünk általános.) A vetületben jelezzük, hogy melyik szál megy alul: szakítsuk meg a rajzunkban ezt a szálat. Az így kapott rajzot a csomó diagramjának szokás nevezni. Triviális csomónak nevezzük azt a csomót, amelynek van olyan vetülete, amiben egyetlen kereszteződés sincs. (Nem nehéz belátni, hogy csak egyetlen ilyen csomó van, így az elnevezés valóban csak egy csomóra mutat.)

Az adott \(K\) csomó vetületében keletkező kereszteződések minimális száma (tehát a lehető legkevesebb kereszteződést tartalmazó vetületben lévő kereszteződések száma) a \(K\) csomó kereszteződési száma, melynek jele (az angol crossing number) alapján \(cr(K)\). A kereszteződési számot alapul véve kezdték matematikusok táblázatokba foglalni a csomókat. Az első ilyen táblázat Tait munkája, aki Lord Kelvinnel (igen, azzal a Lord Kelvinnel, akinek az abszolút zérus fokot is köszönhetjük) kezdett az 1800-as évek vége felé csomókkal szisztematikusan foglalkozni.

De térjünk vissza a kicsomózáshoz. Egy kicsomózási lépés legyen az, hogy a felső szálat elvágjuk, és ez alsó alatt átbújtatva rögtön ismét összeforrasztjuk. Tehát Nagy Sándor módjára megváltoztatjuk a csomót, de csak épp egy kicsit. (Kis Sándor módjára?) A fent említett manőver neve kereszteződés-csere; egy eredetileg alul menő szál hirtelen felül megy, a másik épp fordítva.

A csomó bonyolultságát méri például az, hogy mi a kereszteződés-cserék minimális száma ahhoz, hogy a csomót kicsomózzuk, vagyis egészen a triviális csomóig alakítsuk. Ez a minimális szám a \(K\) csomó kicsomózási száma, más néven a csomó gordiuszi száma (utalva Nagy Sándor fent leírt, kicsit drasztikusabb kicsomózására). Jele (az angol unknotting number alapján) \(u(K)\).

A matematika iránt érdeklődő olvasóban felmerülhet a kérdés, hogy jó-e egyáltalán ez a definíció: létezik-e egyáltalán ez a kicsomózási szám minden csomóra. Ha van olyan kereszteződés-cseresorozat, ami kicsomózza a csomónkat, akkor rendben vagyunk: \(u(K)\) az ilyen sorozatok legrövidebbikének hossza, valamilyen nemnegatív egész szám. De van-e mindig ilyen sorozat? A válasz persze az, hogy van; a bizonyításhoz a következőt kell meggondolni (belátását az olvasóra bízzuk):

Feladat: Tegyük fel, hogy a \(K\) csomónak van egy olyan vetülete, amely a következő (kicsit hosszadalmasan leírható) tulajdonsággal rendelkezik. Van a vetületben egy olyan pont, és abban a pontban egy olyan irány, hogy ha onnan abba az irányba indulunk a csomón, akkor minden kereszteződéshez először a felül menő szálon érkezünk. (Nyilván minden kereszteződést kétszer látogatunk meg, míg az adott pontunkból elindulva és körbe menve vissza nem érünk az adott pontba − a tulajdonság az, hogy az első alkalom mindig a felül menő szálon történik.) Rendelkezzen tehát a vetületünk evvel a tulajdonsággal. A feladat: Lássuk be, hogy ha egy csomónak van a fenti tulajdonsággal rendelkező vetülete, akkor az valójában a triviális csomó.

Ebből a feladatból rögtön következik, hogy a csomónk kereszteződés-cserékkel kicsomózható, hiszen egy tetszőleges vetületet cserékkel olyanná tudunk alakítani, ami a fenti tulajdonsággal rendelkezik, ami (a feladat szerint) viszont a triviális csomó lesz. Bónuszként azt is megkapjuk persze, hogy az \(u(K)\) kicsomózási szám legfeljebb a \(cr(K)\) kereszteződési szám lehet, hiszen a legkevesebb kereszteződést tartalmazó vetülettel indulva legfeljebb annyit kell változtatni, mint a kereszteződések száma. (A figyelmes olvasó azt is beláthatja, hogy \(u(K)\) valójában legfeljebb \(cr(K)\) fele lehet csak − ezen is érdemes eltöprengeni egy pillanatra.)

Az \(u(K)\) kicsomózási szám meghatározásának fő nehézségét az adja, hogy nem tudjuk, melyik vetületet (pontosabban diagramot) kell vizsgálnunk ahhoz, hogy a minimális csereszámot megtaláljuk − és persze egy csomónak végtelen sok diagramja van.

De hagyjuk most a kereszteződési és kicsomózási számokat egy kicsit, és vezessünk be egy műveletet csomókon: az összefüggő összeget. Ehhez vegyünk két csomót, nevezzük ezeket \(K_1\)-nek és \(K_2\)-nek. Tegyük fel, hogy a két csomó a térben úgy helyezkedik el, hogy azok egy síkkal elválaszthatók. Másképp mondva, a diagramjaik a síkon valamely egyenes két különböző oldalán vannak. A két csomóból ekkor egy készíthető (amelyet a csomók összefüggő összegének hívunk majd, és \(K_1\# K_2\)-vel jelölünk): ragasszunk \(K_1\)-hez egy szalagot az egyik végénél, majd a szalag másik végét ragasszuk \(K_2\)-höz úgy, hogy a szalag az elválasztó síkot csak egyszer messe.

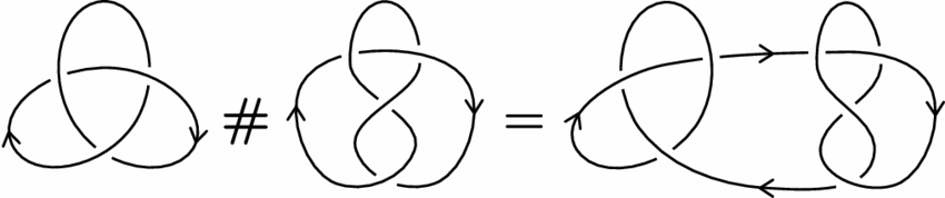
Nem nehéz belátni, hogy az eredmény nem fog függeni sem a választott szalagtól, sem a két csomó sorrendjétől, továbbá ha \(K_2\) a triviális csomó, akkor \(K_1\# K_2\) meg fog egyezni \(K_1\)-gyel.

Kis kitérő: ezzel a művelettel a csomók egészen úgy viselkednek, mint a számok. Valóban, azt mondjuk, hogy a \(K\) csomó prím, ha minden \(K=K_1\# K_2\) felbontás esetén \(K_1\) vagy \(K_2\) a triviális csomó (ez a definíció emlékeztet a prímszámok definíciójára: egy \(p\) szám prím, ha \(p=ab\) esetén \(a\) vagy \(b\) 1-gyel egyenlő). Az analógia tovább vihető: minden \(K\) csomó felírható, mint prímcsomók összefüggő összege, és a felírás sorrendtől eltekintve egyértelmű − csakúgy, mint a számelmélet alaptételében a számok prímtényezős felbontása. Valójában a korábban említett csomótáblázatokban csak a prímcsomók lettek feltüntetve, hiszen a többi ezekből az összefüggő összeg segítségével kirakható.

Mielőtt a fő kérdésre térnénk, még egy egyszerű csomóelméleti konstrukcióval kell megismerkedjünk, ez pedig a tükörkép képzése. Egy \(K\) csomó tükörképe (az angol mirror szó alapján \(m(K)\)) az a csomó, amelyet \(K\)-ból egy síkra való tükrözéssel kapunk. (Mindegy, mely síkot választjuk, az eredmények egymásba alakíthatók.) Ha \(D\) egy \(K\) csomó diagramja, akkor \(m(K)\) egy diagramját úgy kapjuk, hogy \(D\) minden kereszteződésében átcseréljük a felül menő szálat alul menőre, és fordítva.

Egyszerű feladat annak igazolása, hogy \(u(K)=u(m(K))\), vagyis egy csomó és tükörképe ugyanannyi lépésben csomózható ki.

Álljon itt egy példa olyan csomókra, amelyeknek ismert a kicsomózási számuk. A csomócsalád konstrukciója a következő. Vegyünk két szálat a síkon, és csavarjuk meg pozitív irányba \(2n+1\)-szer. (Tehát mindig a bal oldali szál kerüljön felülre.) Ezután a végeket ragasszuk össze, megkapva a \(T(2,2n+1)\) csomót valamilyen pozitív \(n\) számra. Egyszerűen látható, hogy \(n\) lépésben ez a csomó kicsomózható: cseréljünk meg minden második kereszteződést. Annak belátása, hogy kevesebb kereszteződés-cserével nem tudjuk \(T(2,2n+1)\)-et kicsomózni, már sokkal nehezebb. Ehhez bizonyos csomóinvariánsokat kell alkalmazni, amelyek szerencsés módon alulról tudják becsülni \(u(T(2,2n+1))\)-et. Ilyen invariáns például a csomó szignatúrája − ennek bemutatásától ehelyt eltekintünk, mivel néhány további technikai lépésre lenne szükség (de a fogalom, a szingatúra által adott becslés \(u\)-ra, és kiszámolása a fenti csomókra nem igazán nehéz). Például megkapjuk, hogy \[u(T(2,7))=3.\] Ideje most már rátérnünk cikkünk fő problémájára. Természetes kérdés, hogy az összefüggő összeg mennyire bonyolult. Esetleg a két komponens bonyolultságát kell összeadni? A kicsomózási szám esetében természetes kérdés volt, hogy \[\begin{align}&\ \ ?\\ u(K_1\# K_2)&=u(K_1)+u(K_2).\end{align}\]

Megjegyzés: A korábban említett csomóinvariánsok (például a szingatúra) általában additívak, tehát összefüggő összegre a komponensek invariánsainak összegét adják. Természetes elvárás volt tehát hosszú időn át, hogy a fenti egyenlet teljesül.

Jelen cikk címében az említett klasszikus kérdés épp a fenti egyenlőség igaz volta, a megoldást pedig (amely 2025 júniusában jelent meg az arXiv-on) cikkünk további része tartalmazza. A válasz pedig, meglepő módon, és évtizedek várakozása ellenére NEGATÍV.

Mark Brittenham és Susan Hermiller amerikai matematikusok találtak két csomót (valójában a \(T(2,7)\) csomót és annak \(m(T(2,7))\) tükörképét), amelyekre az egyenlőség nem teljesül! Mint korábban említettük, \(u(T(2,7))=3\), és \(u(m(T(2,7)))=u(T(2,7))\) szintén 3. A Brittenham-Hermiller cikk valódi tartalma, hogy \(u(T(2,7)\# m(T(2,7)))\) legfeljebb 5 (a pontos értéket a cikk nem adja meg, az a mai napig nem ismert). Az egyenlőtlenség belátása (amint megvan a megfelelő csomó) nem nehéz: megadható egy diagram, és azon öt kereszteződés, amely kicsomózza a csomót. (Az eredeti bizonyítás valamennyivel bonyolultabb volt, a megfelelő \(T(2,7)\# m(T(2,7))\) diagramot C. Wang és Y. Zhang találta meg − ez utóbbi diagramot mutatjuk be alább.

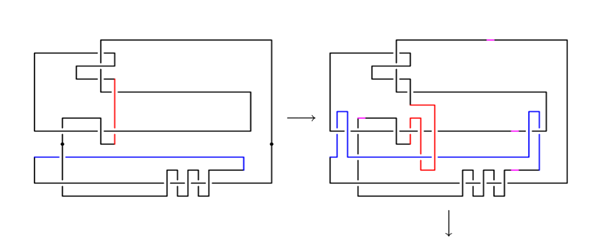
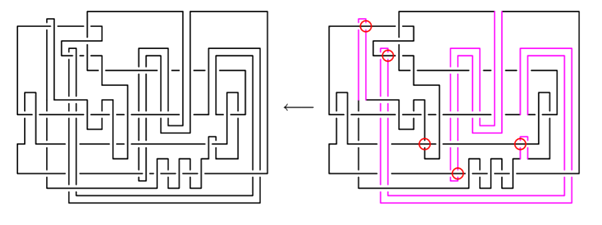
Ez az egyszerű rajz tehát megold egy hosszú ideje nyitott (és nagyon alapvető) csomóelméleti problémát. A szerzők azonban rögtön egy hasonló kérdést ajánlanak az olvasó figyelmébe: Igaz-e az, hogy minden \(K_1\), \(K_2\) csomópárra teljesül, hogy \(u(K_1\# K_2)\) legalább akkora, mint \(u(K_1)\) és \(u(K_2)\) közül a nagyobbik? Ez az elvárás nagyon kézenfekvő. Tegyük fel, hogy \(u(K_2)\) nem kisebb, mint \(u(K_1)\), és tekintsünk az összefüggő összegre úgy, mintha \(K_2\) egy szálát \(K_1\)-é bogoztuk volna. (Ez teljesen rendben lévő interpretáció.) Ha az összefüggő összeg kicsomózási száma kisebb, mint \(u(K_2)\), akkor valójában az történt, hogy \(K_2\) egy szálát bogozva, egy „egyszerűbb” (hamarabb kibogozható) csomóhoz jutottunk, ami ellentmond szemléletünknek. Bár a \[\max(u(K_1), u(K_2))\leq u(K_1\# K_2)\] egyenlőtlenség a fentiek értelmében természetesnek tűnik, precíz bizonyításunk erre még nincs. De nem is baj, fontos, hogy maradjon teendő a jövő csomóelmélészeinek is!

Irodalom:

Mark Brittenham, Susan Hermiller, Unknotting number is not additive under connected sum, arXiv:2506.24088

C. Wang and Y. Zhang, A remark on the counterexample to the unknotting number conjecture, preprint, 2 pp.,arXiv:2507.14265

Stipsicz András
HUN-REN Rényi Alfréd Matematikai Kutatóintézet