A Bolyai János Matematikai Társulat 2004 óta rendezi meg a Rátz László Vándorgyűlésen a Tanárversenyt. Az általános és a középiskolai tanárok részére két kategóriában szervezett 21. verseny feladatait az elmúlt néhány évhez hasonlóan az idén is Fonyóné Németh Ildikó és Fonyó Lajos állították össze. A szellemi erőpróbára a négynapos kora nyári rendezvény második napján, csütörtökön kora délután került sor. A résztvevőknek 90 perc alatt 30 tesztfeladatot kellett megoldaniuk matematikai segédeszközök nélkül.
A feladatok a matematika szinte minden fontos területét érintették, pontos fogalmi ismereteket, szövegértést, logikus gondolkodást és magasszintű problémamegoldó képességet igényeltek a versenyzőktől. Emellett a felnőttek is átélhették azokat az izgalmakat, amelyeket a tanítványaik is érezhettek a hasonló versenyek során. A legnagyobb kihívást talán az időkorlát jelentette a tanároknak.
A versenyen sokan indultak, a vándorgyűlés résztvevőinek közel harmada, 58 közép- és általános iskolában tanító vett részt ezen a programon. Mindkét kategóriában 80% körüli teljesítménnyel lehetett nyerni, az indulók szép eredményeket értek el.
A versenyzők elégedetten távoztak, mivel 60 olyan, a magyar szakirodalomban nem szereplő feladattal és azok megoldásaival gazdagodtak, amelyeket majd jól tudnak hasznosítani későbbi, iskolai szakköri munkájukban.
A részletes eredményeket és a feladatsorokat az ABACUS és a KöMaL folyóiratok egyik őszi számából ismerhetik meg az érdeklődők.
Ízelítőül megmutatunk 4-4 versenypéldát, a középiskolai példák közül a 14., 24., 29. és a 30.-at, az általános iskolai feladatok közül a 13., 18., 26. és a 30.-at.
A versenyen íróeszközön, papíron, körzőn és vonalzón kívül semmilyen más segédeszköz nem használható.
Középiskolai tanárverseny:
14. Az \(ABCD\) négyzetet az \(O\) középpontja körül az óramutató járásával megegyező irányba \(20^\circ\)-kal elforgatva az ábra szerint az \(EFGH\) négyzetet kapjuk. Hány fokos az \(EAD\sphericalangle\)?

| (A) | 20 | (B) | 24 | (C) | 30 | (D) | 32 | (E) | 35 |
24. Andris megrajzolta az \(5\times5\)-ös négyzetrácsban az összes olyan rácsvonalakon haladó útvonalat, amely a bal alsó sarokból a jobb felső sarokba vezet, és 1 egység hosszúságú jobbra vagy felfelé irányuló szakaszokból áll. Minden egyes esetben kiszámította a négyzetrácsnak az útiránytól jobbra eső területét. Az alábbi ábrákon két példa látható. Hány egység az Andris által kiszámolt területek összege?

| (A) | 2520 | (B) | 3150 | (C) | 3840 | (D) | 4730 | (E) | 5050 |
29. Bea véletlenszerűen kiválaszt 3 különböző számot az \(\{1, 2, 3, 4, 5, 6\}\) halmazból, és csökkenő sorrendbe rendezve azokat egy háromjegyű számot képez belőlük. Balázs az \(\{1, 2, 3, 4, 5\}\) halmazból választ véletlenszerűen 3 különböző számot, és ő is csökkenő sorrend szerint felír belőlük egy háromjegyű számot. Mennyi a valószínűsége annak, hogy Bea száma nagyobb, mint Balázsé?
| (A) | \(\dfrac{11}{20}\) | (B) | \(\dfrac{29}{40}\) | (C) | \(\dfrac{3}{4}\) | (D) | \(\dfrac{5}{6}\) | (E) | \(\dfrac{19}{20}\) |
30. Van néhány egyforma négyzet alakú papírlapunk, mindegyiknek az egyik oldala fehér, a másik fekete. 6 papírnégyzetet összeillesztünk, így egy \(3\times 2\)-es téglalap alakú kártyát kapunk. Minden kis négyzet esetén szabadon megválaszthatjuk, hogy a felfelé néző lapja milyen színű legyen. Ha két \(3\times 2\)-es kártyát nem lehet elforgatni vagy átfordítani úgy, hogy pontosan ugyanúgy nézzenek ki, akkor azokat különbözőnek tekintjük. Hány különböző \(3\times 2\)-es kártya készíthető?
| (A) | 20 | (B) | 23 | (C) | 26 | (D) | 27 | (E) | 28 |
Általános iskolai tanárverseny:
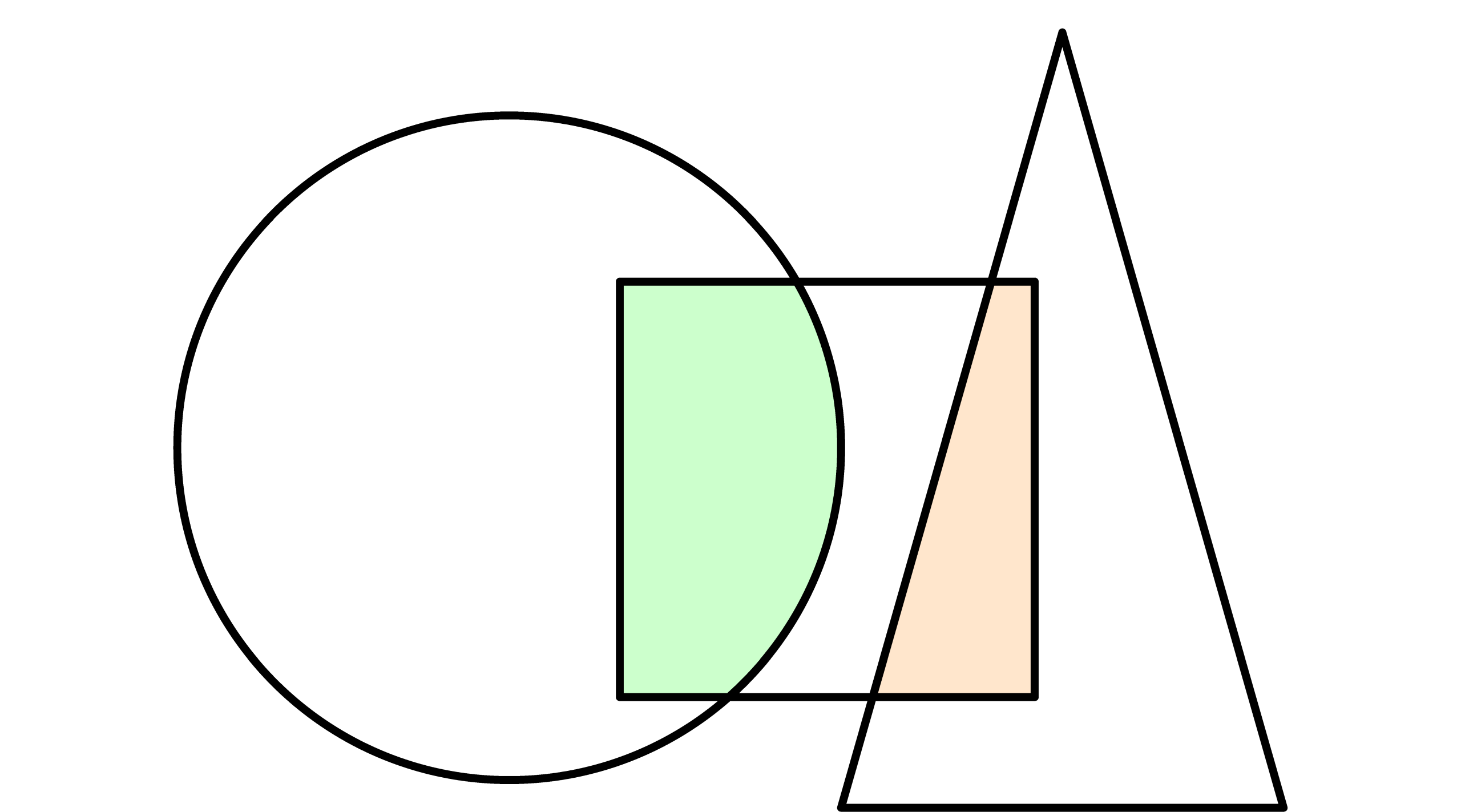
13. Az ábra szerint a körön belül besatírozott tartomány a körnek \(1/6\), a négyzet területének \(1/5\) része. A háromszögön belül besatírozott tartomány a háromszögnek \(1/9\), a négyzet területének \(1/4\) része. Ha a területek aránya \(T(\text{kör}):T(\text{négyzet}):T(\text{háromszög})=24:m:n\), akkor mennyi \(m+n\) értéke?

| (A) | 44 | (B) | 48 | (C) | 50 | (D) | 65 | (E) | 69 |
18. Az ábrán látható 5 négyzet mindegyikének területe \(16~\text{cm}^2\). Az \(A\), \(B\), \(C\), \(D\) pontok csúcsai egy-egy négyzetnek, \(E\) pedig a \(CD\) szakasz azon pontja, amelyre az \(AE\) szakasz felezi a teljes alakzat területét. Hány cm hosszú a \(CE\) szakasz?

| (A) | \(\dfrac{9}{2}\) | (B) | \(\dfrac{24}{5}\) | (C) | 5 | (D) | \(\dfrac{21}{4}\) | (E) | \(\dfrac{16}{3}\) |
26. Egy dobozban 3 piros és 2 fehér golyó van. A golyókat egyesével, visszatevés nélkül, véletlenszerűen húzzuk ki a dobozból addig, amíg az összes piros vagy az összes fehér golyót ki nem húzzuk. Mennyi a valószínűsége annak, hogy a 3 piros golyó kihúzásra kerül?
| (A) | \(\dfrac{3}{10}\) | (B) | \(\dfrac{2}{5}\) | (C) | \(\dfrac{1}{2}\) | (D) | \(\dfrac{3}{5}\) | (E) | \(\dfrac{7}{10}\) |
30. Az \(\overline{abcde}\) ötjegyű számot ,,hullámvasút” típusú számnak nevezzük, ha megfelel az alábbi feltételeknek:
– \(a\), \(b\), \(c\), \(d\), \(e\) 1-től 9-ig terjedő különböző egész számok,
– \(d>c\) és \(d>e\),
– \(b>a\) és \(b>c\).
Hány ilyen tulajdonságú ötjegyű szám létezik?
| (A) | 126 | (B) | 1260 | (C) | 1440 | (D) | 1512 | (E) | 2016 |
Fonyóné Németh Ildikó, Fonyó Lajos