Kutató diákok, avagy miből lesz a cserebogár…

Sok évvel ezelőtt egy karinthys diák keresett meg, hogy mentoráljam a kutatómunkáját. A Karinthy Gimnázium volt az első IB iskola Magyarországon, tehát az első, amely International Baccalaureate fokozathoz vezető középiskolai képzést nyújtott. A diploma megszerzésének egyik feltétele az „Extended Essay” (egy mentorált kutatómunka) és annak írásbeli összefoglalója, amit egy külsős, nemzetközi bizottság bírál el¹.

Nagyon tetszett ez a fajta kihívás, gondolkodtam rajta, miképp tudnám saját Fazekas gimnazista diákjaimnak bevezetni. Nem akartam az érettségivel versenyezni, de fontosnak tartottam a kutatómunkát a pályaválasztás előtt. A 10. évfolyam mellett döntöttem. A kollégákkal egyeztettem és a diákoknak is tetszett az ötlet. Nem volt külsős bizottság, a nebulók esszével és egymásnak tartott előadással készültek.

Csodálatos élményeink voltak már az első évben. Olyan értékekről adtak számot a diákok, amilyenekre nem számítottam. Káldi Tamás a felhőkarcolókról tartott remek ismertetőt, a kiváló fizikus Karsa Anitát szerencsére nem tudtam lebeszélni, hogy a Queen együttesről beszéljen nekünk órákon keresztül, erre vágyott, és így is díjas lett az Eötvös versenyen.

Tapasztaltam, hogy a 7-8-os diákoknak minden egyes tanóra egy külön világ, gyakran nem emlékeznek vissza, nem tudnak építeni arra, ami korábban történt, ráadásul tankönyvük sincs. Én magam nem voltam olyan rendezett, hogy rendszeresen megnézzem a füzetüket, vagy jegyzetelésre tanítsam őket. Ehelyett elvártam tőlük, hogy tanév végére saját maguknak állítsanak össze valamiféle lexikont, és ennek alakulását alkalmanként ellenőriztem. Ez szerencsés kihívás volt a gyerekeknek, 10. évfolyamra hárman összeálltak és egy színvonalas internetes lexikont szerkesztettek össze. Szabó Dávid volt a matek, Balogh Máté a fizika rész kidolgozója, míg Danka Miklós felelt a webes megvalósításért. Lásd: http://lexikon.fazekas.hu/.

Amikor Tomon Istvánt kérdeztem, hogy miről írt, akkor egy olyan számelméleti állítást fogalmazott meg, amit nem akartam elhinni. Felhívtam egyetemi tanáromat, Freud Róbertet, szavaira már nem, csak elképedésére emlékszem, és hogy a Rényi Matematikai Kutatóintézet Számelméleti Osztályának akkori vezetőjét, Ruzsa Imrét ajánlotta. Amikor szabadkozva megkerestem őt, és elmondtam Pityu állítását, felajánlotta, hogy az ifjú tartson egy előadást a következő péntek délután az intézetben. Ruzsa Imre Matolcsi Mátéval és velem hallgatta az előadást, a végén percekig néma csöndben figyelte még a táblát, aztán amikor megszólalt, ennyit mondott: „Ez csinos, nagyon csinos!”.

Bóra Eszter története különösen kerek lett. Ő megkérdezte, hogy én mit gondolnék jó témának neki, és mivel emlékeztem az elpusztult kőröshegyi zsidó közösségről írt korábbi remek kutatómunkájára, egy hasonló témával álltam elő: „Itt van az Arany Dániel matematikaverseny; Arany Dániel alapította a Középiskolai Matematikai és Fizikai Lapokat is; én még annyit tudok róla, hogy éhen halt a gettóban. Jó lenne többet tudni róla.” Eszter egy kis könyvvel válaszolt, amelynek néhány példánya már forgott a tanári karban és azon túl, amikor egy péntek délután előadást tartott a témában a diákoknak. Aztán mennie kellett, mert a Rényi Intézetben várták az Arany Dániel Matematikai Tanulóverseny eredményhirdetésére, ahol feladatmegoldásaira dicséretet kapott, és mellesleg a felvezetésben az ő könyvéből idézve emlékeztek meg a verseny névadójáról. Írásával később a Természet Világa pályázatán nyert díjat Eszter².

Egy szívemnek nagyon kedves kutatómunka, amelyet Szabó Dávid végzett, kissé később, nem ebben a keretben történt. Nem tudom már, hogyan akadtam bele egy szép összefüggésbe a Pascal-háromszöggel kapcsolatban, de amikor Surányi László kollégám azt mondta, hogy nem ismer rá elemi megoldást, akkor bepöccentem, és csináltam rá egyet, sőt általánosítottam is. Amikor bevittem az osztályba, Dávid lelkesedett fel a kérdésen, meg is oldotta, aztán az általánosítást is elintézte. Mondtam neki, hogy szerintem érdemes lenne továbbmenni a gamma-függvénnyel, de azt én már nem látom át. Dávid később elment Cambridge-be három évre, és utána írt egy cikket az azonosság messzemenő általánosításairól: https://archive.org/details/eureka-63/page/18/mode/2up~.

Amikor 11. évfolyamuk elején az orvosnak készülő Fésűs Szilvia és Szőllősi Annamária a matematika fakultációt választották, én is csodálkozva kérdeztem rá döntésükre, amire így válaszoltak: „De Tanár Úr, mi még nagyon sok biológiát fogunk tanulni az orvosin is, de matekot csak most tudunk!” – kevés diák van, aki így céltudatos és aki ilyen fiatalon is a közt szolgálja: fordításuk révén diák és tanár is hozzáfér az elemi geometria legkülönösebb konfigurációjának, Feuerbach tételének bizonyításához: https://matek.fazekas.hu/solo/szollosi_feuerbach/.

Nem tudtam róla, hogy fazekasos kísérletem előtt pár évvel Horváth Eszter a Szegedi Egyetemen már meghirdetett egy kutatási pályázatot diákoknak. Ez nagyon jól jött, az egyetemi szintű bizottságnak beküldött kutatómunka mélyebb átgondoltságot, pontosabb kidolgozottságot követel meg, mint egy iskolai előadás, vagy dolgozat, de remek folytatás lehet az iskolai munka után.

Tomon István méltán nyert ott I. díjat 2008-ban, de egy másik diákom, Wágner Zsolt, következő évi I. díjas munkájára is jól emlékszem. A Steiner-rendszerek nagyon szép, szimmetrikus részhalmazrendszerek, elég könnyű felírni a feltételeket, hogy milyen paraméterértékek esetén létezhetnek csak, de messze nem olyan nyilvánvaló konstruálni megfelelő rendszereket a nem kizárt értékekre. Zsolti megcsinálta a konstrukciókat. Úgy tíz évvel később, amikor már egy ideje Londonban éltem, Zsolt meghívott egy előadására, amit vendégként tartott a London School of Economics-en, ahol egy nagyon erős kombinatorikai tanszék működik. Ez nekem nagyon nagy élmény volt, ritka alkalom, mert nem nőttem bele a londoni matematikai életbe úgy, ahogy még Pesten benne voltam.

A következő osztályomban már bejáratottabban ment a kutatómunka, de kevésbé emlékszem a részletekre, nagyon nehéz két év volt nekem 2013 és 2014, az utóbbi nyarán mentem ki Angliába. Csigi Máté kétszer is díjazott lett, mindkétszer a tér és a sík kapcsolatát vizsgálta, de nagyon különböző kérdések kapcsán, és ehhez hasonló dologban ügyeskedett mostani londoni diákom, Sarvesh is (nyilván az én hasonló érdeklődésem is közrejátszik ebben). Maga Balázs és Török Misi együtt dolgoztak az egyetemi pályázatra, I. díjas munkájuk címe „Háromszögszámok és négyzetszámok összegéről” volt. Balázs így mesélte el az inspirációt: „A nyíregyházi hálószobaajtómon az üveg háromszögrácsban elhelyezkedő körlapokkal volt díszítve. Egyszer betegen otthon feküdve felfigyeltem arra a rácsról vizuálisan könnyen leolvasható összefüggésre, hogy minden háromszögszám felírható négy kisebb háromszögszám összegeként. A négy helyett három is mondható. De kettő…? Ebből indult ki az egész, s derült ki, hogy igencsak hasonlít ez az egész ahhoz, amit a négyzetszámokról addigra már tanultunk Nálad, s nagyon élveztem. A kutatás közösségileg is hasznos melléktermékeként pedig néhány KöMaL-feladatot javasoltam az azt követő évben, ami háromszögszámok összegeivel kapcsolatos.”

Angliában egy ideig nem is tanári állásban, hanem „Exam Officer and Data Manager” státuszban dolgoztam, de lelkesen tartottam a munkaidőn túl a Cambridge-be készülőknek szakkört. Amikor feladtam nekik Wallis integrálokat tartalmazó táblázatát, Khalid Hassan felismerte a mintát, de kérésemre, hogy bizonyítson, váratlan irányba indult el. Végül eljutott a megoldáshoz, de ehhez egy rendkívül szokatlan Pascal-háromszöges azonosság igazolására volt szükség, ami egy együttható reciprokát fejezte ki más együtthatókkal, és jól bele kellett ásnia magát a szitaformulába, hogy befejezze a gondolatmenetet. Lenyűgöző volt Khalid kifejezésmódja, tartalmas, szép dolgozatára I. díjat kapott a Polygon Pályázaton, ez biztosan segítséget jelentett neki, hogy bejusson a Cambridge Egyetemre.

Belekezdtünk egy új matematikaszakköri iskola létrehozásába Londonban; egy ideig elemibb feladatokra kellett koncentrálnom, mint a diák-kutatómunka. Bő két éve viszont az oktatás lényeges elemévé tettem a Szegedi Egyetem pályázatát. Talán ez Magyarországról nem látszik, de amit Horváth Eszterék csinálnak – eleinte Pintér Lajos, majd Hajnal Imre zsürielnök szakértői figyelmével – az egyedülálló, nagyon jó, és változó világunkban is remekül megállja a helyét. Organikusan szép és megnyugtató, hogy az inspiráló pályázat szervezését egy volt versenyző, ma már egyetemi oktató, Kunos Ádám viszi tovább. Nagyon jó, hogy néhány éve a BME megnyitotta kutatási programját, a BME-TDK-t középiskolásoknak is. A programban átélt első tapasztalatairól az Érintőben nemrég számolt be Burai Pál egyetemi oktató.
A Szegedi Egyetemről kerül a katedrára a nem fővárosi tanárok jelentős része. Kutatási pályázatuk a középiskolai tanárokat is ösztönzi, az ő nyitottságukra és érdeklődésükre is alapoz, úgy érzem, engem is megszólít.

Szakköreimen és az emailes tájékoztatókban februárban beszélek először a Szegedi Egyetem versenyéről a diákoknak, aminek határideje a következő év januárja. Elsősorban a 11-edikeseknek ajánlom, akik ugyan nyár elejéig a GCSE vizsgájukkal (kisérettségi) vannak elfoglalva, de utána egy viszonylag szabadabb évük jön. Egy évvel később, az egyetemi jelentkezés és az A-level vizsgák küszöbén nehéz már a kutatásra koncentrálni. Persze a tizedikeseknek is megfelelhet a kutatás, ezt két első díjas angliai nebulóm is igazolja.

A gyerekek a tavaszi szünet egy részében olvasnak, problémákon gondolkodnak, témát keresnek. Van aki maga jön elő témával, van, aki ebben az értelemben nem annyira önálló, az ilyen diákot kikérdezem, hogy milyen területek érdeklik, vagy mely korábbi kérdések izgatták és javasolok újabbakat, vagy ajánlok nekik cikket, könyvet.Daria Gal hozott egy témát, azon nem találtunk jó fogást, ezért később másikat javasolt, ami nekem is új volt. Egy majdnem teljesen igazolt sejtés szerint minden síkbeli zárt görbén található négy különböző pont, amelyek egy négyzet csúcsai. Kerestünk eseteket, ahol elemien megtalálható a négyzet, pl. egy háromszögben, négyzetben. Dasha vizsgált nehezebb eseteket, mint egy parabolaív egy azt lezáró húrral és meglepetésemre a folytonos függvényekről való olvasmányai után elintézett egy sokkal kevésbé elemi esetet: bizonyította ilyen négyzet létezését olyan formára, amelynek egyik oldala az x-tengely egy szakasza, másik része pedig egy folytonos függvény grafikonja, amelynek két zérushelye a szakasz két végpontja.

Ryan Bashkar lelkesedett a véges geometriákért. Ehhez kapcsólódó példákat kért, még és még. Én inkább frusztrált voltam, ez így nem volt igazi kutatómunka, bár fokozatosan igazán nehéz kérdésekig jutottunk el. Amikor el kellett döntenie, hogy két Steiner-rendszer ekvivalens-e, akkor elkezdte ügyesen használni a számítógépet, és a gép eredményei nélkül megfogalmazható szép indokot talált a különbözőségre. Aztán tovább vizsgálódott a géppel és észrevett valamit, amit sokáig hiába magyarázott nekem. „Ezt miért csinálod?” „Oké, de hogy jön ez a Steiner-rendszerekhez?” „Várjál, mit állítasz?” „Úristen, ez tényleg igaz?” „És ezt te tudod igazolni?” – ezek voltak sorban a reakcióim. Korábban kölcsönadtam neki a könyvet, ami Tomon Pityut is elindította egy másik, de a kvadratikus maradékok miatt pont idevágó témában, de a „gaz” Ryan kikerülte a könyvet, és közvetlenül a köbös maradékokkal rendezte le a témát. Azt is igazolta, hogy az ő Steiner-rendszerei különböznek Zsolt rendszereitől.

Dasha és Ryan is I. díjat kaptak két éve a Polygon Pályázaton, és tanév végi összejövetelünkön ízelítőt adtak a többi diáknak kutatásukból.

Van egy nyári „Super Maths Camp”-ünk, ezen a gyerekek egymást oktatják, egymásnak adnak fel példákat és tartanak előadásokat. Ez a tábor és a rá való készülés is része lehet a kutatási folyamatnak. Tavaly nyáron például Ran Sharkar a gráfokról mesélt, Siddharth Shah a szita-formuláról és a Stirling-számokról. Mindketten hosszú utat jártak be sok olvasással, egymásnak tartott előadásokkal, a számítógép rendszeres alkalmazásával, míg január végén beadták távolról egymáshoz kapcsolható munkáikat a Szegedi Egyetemen. Rian I. míg Siddhart II. díjat ért el. Két másik diákom csak ősszel fogott bele a kutatásba, rövid idő alatt sokat tanultak és dolgoztak; ennyi idő III. díjhoz és Kiemelt dicsérethez volt elegendő.

Május legeleje van, néhány diák már nekifogott egy későbbi lehetséges kutatómunka első lépéseinek, néhányan belelkesedtek, de még a vizsgáikra koncentrálnak. Izgatott vagyok, ki milyen irányba megy. Lassan 60 éves rutinos tanár vagyok, de néha már unom magam, nagyon jólesik, hogy a diákok elvisznek olyan utakra, amelyekről már magam is álmodoztam vagy olyanokra, amelyek eszemben sem voltak.

Tomon István, már ifjú matematikusként, több mint 50 megjelent cikke után írja: „Visszagondolva a középiskolára, de főleg az egyetemre, kicsit hiányzott, hogy jobban ki legyünk téve matekkutatásnak. Rengeteg probléma van, aminek a megoldására egy tehetséges diáknak is van esélye”

Ezt mondja a népdal: „Sej, Nagyabonyban csak két torony látszik, de Majlandban harminckettő látszik. Inkább nézem az abonyi kettőt, mint Majlandban azt a harminckettőt.”

A matek egyszerűbb. Olyan diákpályázat, mint a Polygon Pályázat, amit Horváth Eszterék 20 éve megálmodtak és működtetnek a Szegedi Egyetemen, a hires Majlandban vagy Londonban 0 darab van.

A Polygon Pályázat honlapja: https://www.math.u-szeged.hu/~horvath/palyazat.htm.

Hraskó András, Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.
London School of Mathematics and Programming,
korábban: Fazekas Mihály Gyakorló Ált. Iskola és Gimnázium, Budapest

Köszönetnyilvánítás

A szerző köszönettel tartozik a Fazekas Gimnázium vezetőségének, tanárainak és diákjainak a szabad, intellektuális légkörért, különösen Surányi Lászlónak és Pataki Jánosnak a kutatással kapcsolatos inspirációikért, valamint a London School of Mathematics and Programming alapító vezetőinek, Anastasia és Fred Stone-nak az állandó támogatásért.

Appendix

1. Kvadratikus maradékok. Könnyű ellenőrizni, hogy a négyzetszámok utolsó jegye a 0, 1, 4, 5, 6, 9 számjegyek közül kerülhet ki. Ehhez hasonlóan vizsgálható tetszőleges 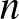$n$ pozitív egész szám esetén, hogy mi lehet és mi nem lehet négyzetszám 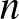$n$ -es maradéka. 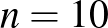$n=10$ esetén ezt láttuk:

0 – igen
1 – igen
2 – nem
3 – nem
4 – igen
5 – igen
6 – igen
7 – nem
8 – nem
9 – igen

Tomon István állítása 16 éves korában:Tetszőleges véges igen-nem sorozathoz tartozik egy korlát úgy, hogy a korlátnál nagyobb minden egyes p prímszám esetén, ha a p-vel való lehetséges osztási maradékok, tehát 0, 1, 2, …, 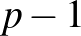$p-1$ mindegyikére odaírjuk, hogy „igen” (lehet négyzetszám maradéka) vagy „nem” (nem lehet négyzetszám maradéka), akkor az előre adott sorozat ott lesz benne a válaszokban egymás után, hézag nélkül.

2. A Pascal-háromszög:

Ha felírjuk a Pascal-háromszög középső oszlopának első néhány elemét az eredeti és fordított sorrendben is, akkor a számok szorzatának összege mindig a 4 egy hatványa lesz. Például:

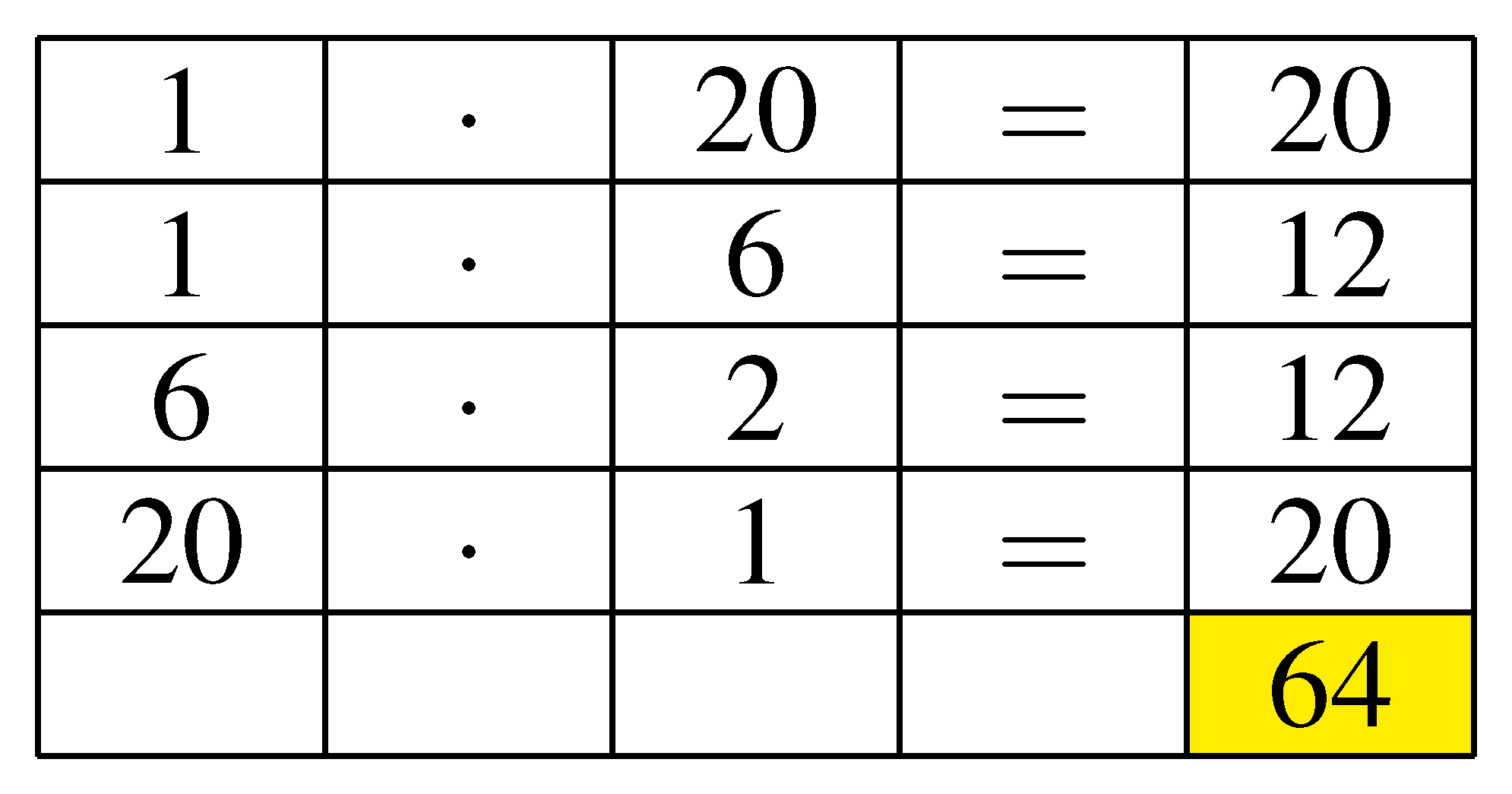
Próbálkozhatunk két különböző oszloppal is, de ahhoz felfelé is folytatnunk kell a Pascal-háromszöget, és az egyiket rendesen, a másikat fordítva kell leírnunk. Ha például a középső oszlop két oldalán ugyanakkora távolságban választjuk az oszlopokat, akkor minden kerek.

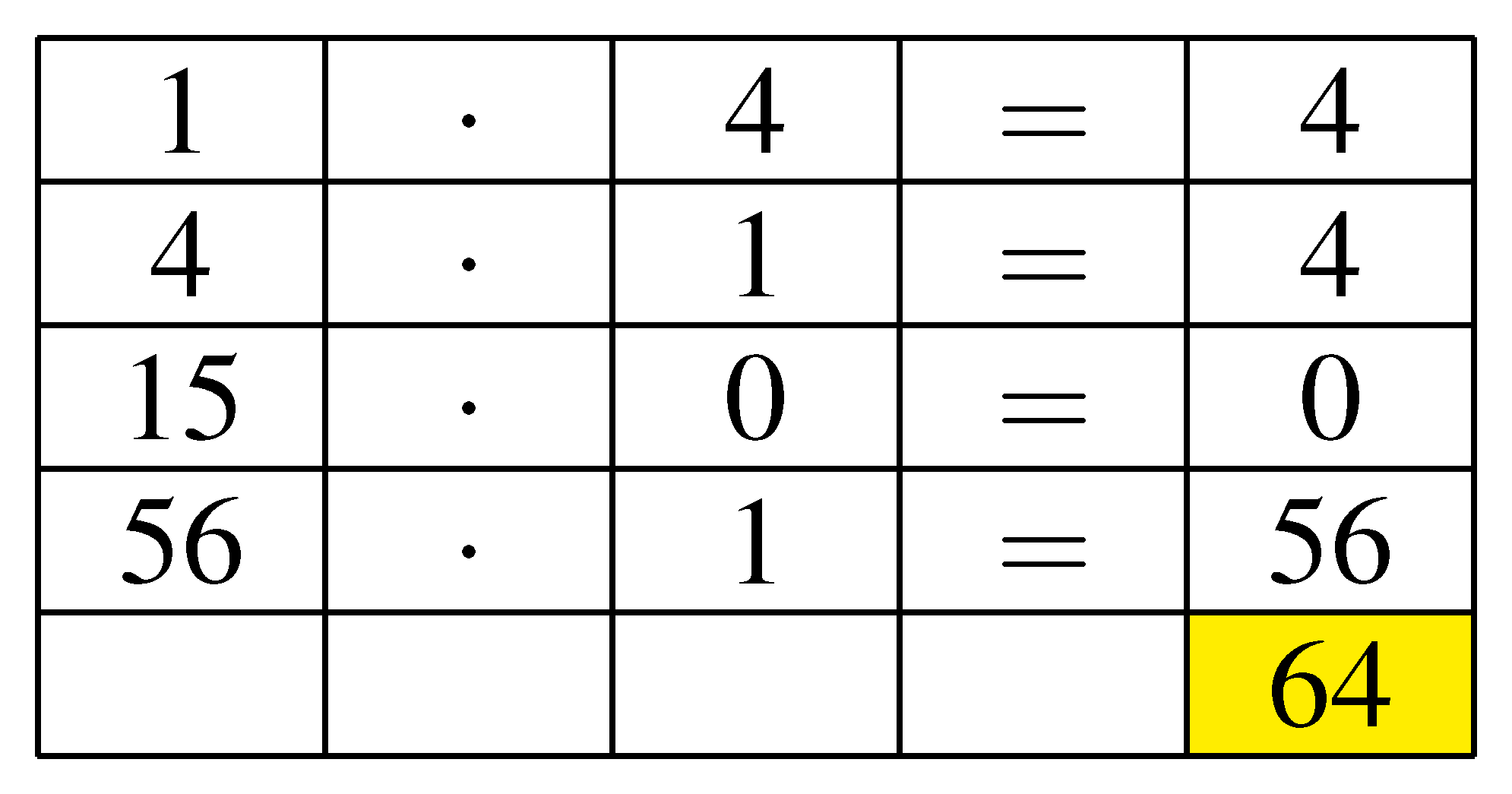
Ha nem ilyen szépen választunk, akkor mi lesz a jó formula?

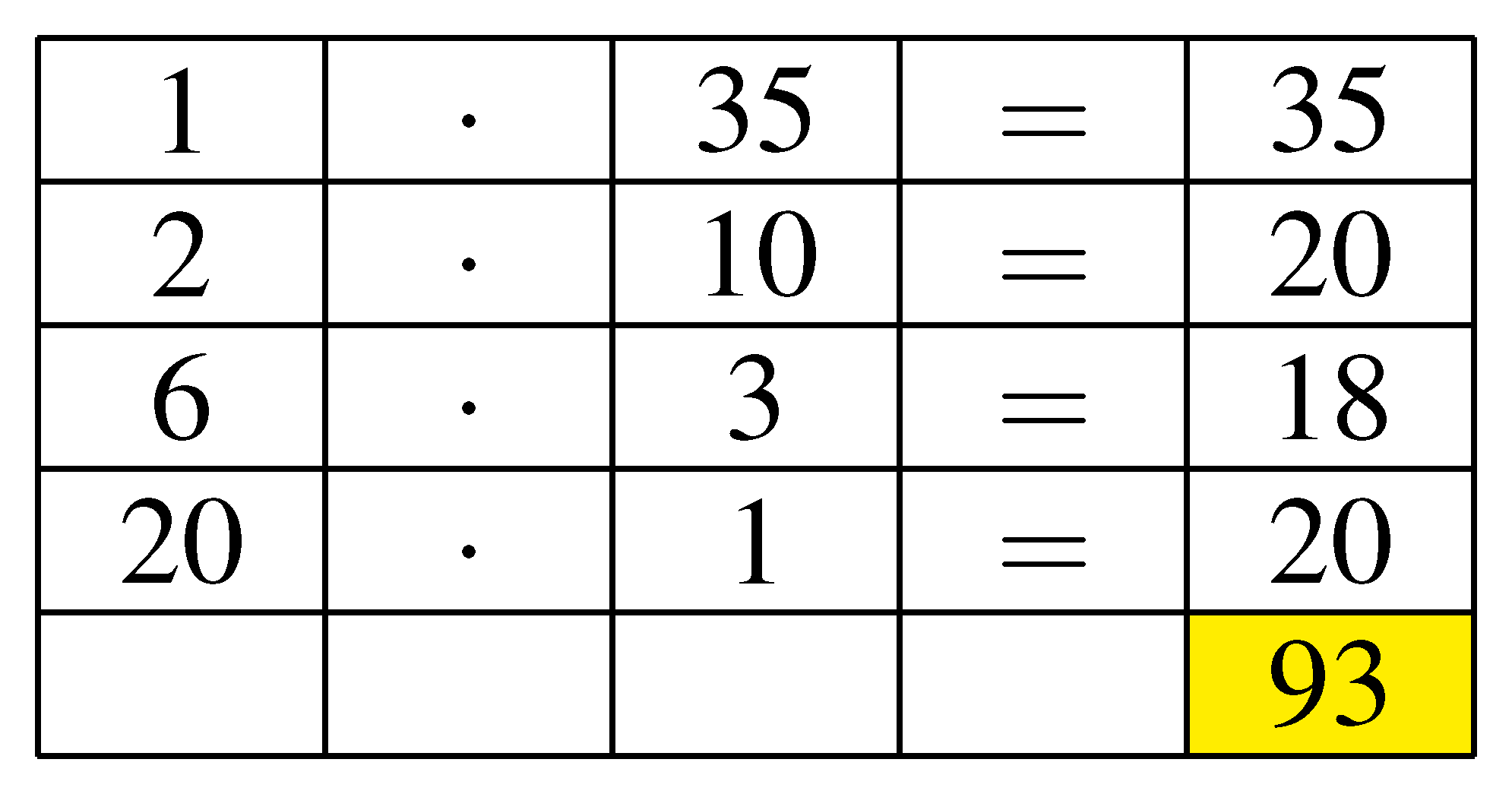
Furcsa, a Pascal-háromszög egy sorában: $1+8+28+56=93$ .

Szabó Dávid nemcsak függőleges, hanem ferde vonalakra is talált formulát.

3. Töltsd ki Wallis táblázatát, ahol 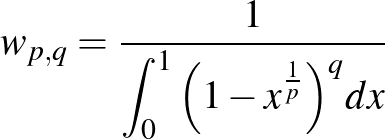$w_{p,q}=\frac{1}{\displaystyle\int^1_0{{\left(1-x^{\frac{1}{p}}\right)}^qdx}}$ $.$

$\begin{picture}(8,4)\footnotesize \put(0,0){\line(1,0){8}}% \put(1,0.5){\line... ...\{ makebox(0,0)[b]\{$=$\}\} put(4.5,2.1)\{ makebox(0,0)[b]\{4\}\} \end{picture}$

Khalid lemmája:

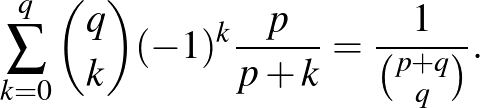
$\displaystyle \sum^q_{k=0}{\binom{q}{k}(-1)^k\frac{p}{p+k}=\frac{1}{\binom{p+q}{q}}}.$

Találsz egy kombinatorikai vagy valószínűségszámítási feladatot, amelyre az egyenlet jobb oldala egy rövid válasz, a bal oldala pedig egy szitaformulás megoldás?