2025 májusában indul az ELTE Informatikai Karán a Higher Observational Type Theory (HOTT) ERC projekt [1]. A HOTT projekt célja egy új típuselmélet kifejlesztése, amelyben teljesül az izomorf struktúrák egyenlőségének elve. Az alábbi írás ennek a projektnek a hátterét világítja meg.
Titánok küzdelme
A típuselmélet búvópatakként mindig is jelen volt a formális tudományokban. Bár a gyakorló matematikus csak a matematikatörténet órán találkozott vele, a matematikai logika nem felejtette el, az informatikában és a számítástudományban pedig a legváratlanabb helyeken futhatott bele a kutató. Karrierje akkor indult, amikor a matematika 20. századeleji megalapozási válságára kellett megoldást találni. Mint ismeretes, ekkor a naiv halmazelmélet szekrényeiből sorra hullottak ki (ellentmondások képében) a csontvázak és ejtették kétségbe a végső bizonyosságra vágyó matematikusokat. Ekkor három nézet rivalizált egymással. A Brouwer-féle intuicionizmus az ember által jól átlátható, biztonságos területre akarta korlátozni a matematikai tevékenységet, talán túl féltő módon is. Hilbert javaslata az volt, hogy a matematikai elméleteket fogjuk fel szabatosan formalizált szimbólumrendszerekként, amelyek ellentmondásmentessége felett véges számelméleti eljárások őrködnének. Russell típuselmélete az önmagára hivatkozó mondatok alkotását tiltotta meg olymódon, hogy a matematikai létezőket típusokba sorolta: volt az egyedi dolgok típusa, ez egyedi dolgok összességeinek típusa, és így tovább. A titáni küzdelemben végül is mindegyik elmélet elvérzett, a nevető negyedik a halmazelmélet lett.
Mint oly sokszor, a matematikusok az eukleidészi axiomatikus módszerhez fordultak, posztulálva a problémamentesnek tűnő állítások egy részét, de vigyázva arra, hogy a dolgok közti demokratizmus megmaradjon és minden halmaz egyetlen nagy osztályba kerüljön, a típushierarchiákba sorolás helyett. Így vált a formális-axiomatikus halmazelmélet a megalapozási válság egyfajta megoldásává, legalább is egy időre. A titánok megfontolásai ugyanis egyáltalán nem voltak érvénytelenek. Egy új, a 70-es években Per Martin-Löf által megalkotott típuselmélet nagyon sokat megőrzött azokból a gondolatokból, amelyekre a korai három nézet alapult. Ilyen volt például az intuicionisták azon értelmezése, hogy a matematikai állítások voltaképpen feladatok, amelyek megoldása konstruktív eljárás. A bizonyítások így programokká válnak. Vagy ami a Hilbert-féle iskola eredménye volt és Gentzen nevéhez fűződik, hogy az axiómákra alapuló levezetési rendszert le lehet váltani egy a mindennapi matematikai gyakorlatra sokkal jellemzőbb, úgynevezett természetes levezetési rendszerre.
A következő bekezdéseket a Martin-Löf-féle típuselméletnek fogjuk szentelni, amely egyszerre kiváló alap a nagy kifejezőerejű, magas szintű programozási nyelvek leírására és a matematikai bizonyítások emberi léptékű számítógépes modellezésére.
Megérett az idő
Az idő előrehaladtával személyi számítógépeink kapacitása olyan nagy lett, hogy minden további nélkül elfér bennük a teljes egyetemi matematika anyag, és képessé váltak annak a gyors ellenőrzésére is, hogy egy adott bizonyítás valóban helyes-e. Ugyan a Négyszíntétel gépi bizonyítása ellenőrzésének teljes lefuttatása 6 órát vett igénybe, egy szokásos méretű cikkben szereplő állítások bizonyításának gépi ellenőrzése egy-két percnél ritkán tart tovább. Nagyon úgy tűnik, hogy a matematika számítógépes formalizálásáért és a bizonyítások legalább félig automatikus kezeléséért vívott harcot a komputációsan jól viselkedő Martin-Löf-féle típuselmélet illetve ennek 21. századi variánsai nyerték, mint pl. az induktív konstrukciók kalkulusa (Calculus of Inductive Constructions, Coq) és a kubikális (homotópia) típuselmélet (Cubical Type Theory, Cubical Agda).
Na, de kik ellenőriznek bizonyításokat számítógéppel?
1. Akik a cikkük megjelenése után 24 évvel találják meg benne a hibát, és innentől nem bíznak meg a saját bizonyításaikban [23].
2. Akik annyira technikai jellegű és nehéz bizonyítást írnak, hogy félnek, hogy valahol rejtezik egy hiba, és csak akkor tudnak nyugodtan aludni, ha a számítógép ellenőrizte az egészet [20].
3. Akik megelégelték a várakozást a cikkük elbírálására [10].
4. Akiknek nem tetszik [5], hogy a cáfolat [14] után 17 évet kell várakozni arra, hogy visszavonjanak egy hibás cikket [21].
5. Akik kedvtelésből az egész egyetemi matematika tananyagot belekódolták a Lean számítógépes bizonyító rendszerbe [18].
És akkor még nem is beszéltünk olyan előnyökről, mint hogy az interaktív bizonyítás-asszisztensek milyen jól az ember keze alá dolgoznak, és hogy a jóvoltukból nem kell egy éppen ráérő és kellőképpen hozzáértő kollégát terhelnünk azzal, hogy az érvelésünk helyességére, ugyan bólintson már rá. A legtöbb számítógépes bizonyítás-ellenőrző program (olyanok, mint az Agda, Coq, Isabelle/HOL, Lean) nem a halmazelméletre, hanem a típuselmélet Per Martin-Löf-féle felépítésére [17] épül.
Új tömlőbe új bort
A matematika formális megalapozását lehet tisztán filozófiai témának tekinteni: a legtöbb matematikus nem foglalkozik azzal, hogy a halmazelmélet axiómáival és az elsőrendű logika szabályaival pontosan hogyan kódolható a munkájuk. Ha azonban a bizonyításokat szeretnénk számítógéppel ellenőrizni, akkor ez praktikus problémává válik: ki kell választani egy formális rendszert, amelyben a bizonyításellenőrzés történik. A Martin-Löf-féle típuselmélet nem csak a matematika konstruktív megalapozására alkalmas, hanem számítógépes programnyelvként is kiválóan megállja a helyét. (Szokás a programozási nyelvek típusrendszereinek elméletét is típuselméletnek hívni, de mi most típuselméleten Martin-Löf típuselméletét értjük.) Nézzük tehát, miben különbözik egymástól a típuselmélet és a halmazelmélet!
A felszínen először a jelölésbeli különbségek tűnnek fel: halmaz helyett típust mondunk, a típusok elemeit termeknek nevezzük, és 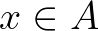 helyett
helyett 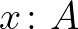 -t írunk. A kettőspont nem is szokatlan jelölés, az
-t írunk. A kettőspont nem is szokatlan jelölés, az 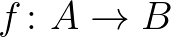 olyan, mintha azt mondanánk, hogy az
olyan, mintha azt mondanánk, hogy az 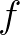 típusa az
típusa az  -ból
-ból 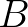 -be képező függvény típus. Menjünk mélyebbre!
-be képező függvény típus. Menjünk mélyebbre!
Reprezentáció-függetlenség.
A típuselmélet egy magas szintű nyelv: a halmazelmélet úgy viszonyul a típuselmélethez, mint a gépi kód mondjuk a Python nyelvhez: amikor Pythonban programozunk, nem kell eldöntenünk, hogy pontosan melyik memóriacímen tárolunk egy értéket, hanem csak adunk egy nevet a változónknak, aztán majd az adott szoftver és az operációs rendszer gondoskodik arról, hogy azt a memóriában valahol tárolja. Amikor halmazelméletben megadjuk a természetes számokat, el kell döntenünk, hogy a Zermelo-féle (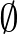 ,
, 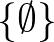 ,
, 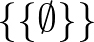 , ...) vagy a von Neumann-féle (
, ...) vagy a von Neumann-féle (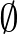 ,
, 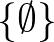 ,
, 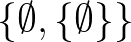 , ...) kódolását választjuk (vagy egy ezektől is különbözőt). A típuselméletben nem kell kódolást választanunk, a természetes számokat az univerzális (kategóriaelméleti) tulajdonságukkal adjuk meg. Ez ahhoz hasonló, mint a Peano-aritmetika elsőrendű nyelvében dolgozni a halmazelmélet helyett. Az informális matematikához emiatt közelebb áll a típuselmélet: kevesebb kódolásra van szükség, amikor a szóbeli informális matematikát formalizáljuk.
, ...) kódolását választjuk (vagy egy ezektől is különbözőt). A típuselméletben nem kell kódolást választanunk, a természetes számokat az univerzális (kategóriaelméleti) tulajdonságukkal adjuk meg. Ez ahhoz hasonló, mint a Peano-aritmetika elsőrendű nyelvében dolgozni a halmazelmélet helyett. Az informális matematikához emiatt közelebb áll a típuselmélet: kevesebb kódolásra van szükség, amikor a szóbeli informális matematikát formalizáljuk.
Reynolds absztrakcióról szóló cikkéből [19] idézzük az alábbi fabulát (tartalmi fordítás).
„Volt egyszer egy egyetem, ahol ha egy professzor erkölcsi turpisságot követett el, azonnal kirúgták. Az erkölcsi turpisság definíciója a következő volt: tanórán hamisat állítani. Nem meglepő, hogy ezen az egyetemen nem tanítottak informatikát, volt azonban egy jónevű matematikai intézetük. Ebben az intézetben egyik évben olyan sokan voltak kiváncsiak a komplex analízis tárgyra, hogy két párhuzamos kurzust indítottak. Az egyik kurzuson Descartes professzor elmondta, hogy egy komplex szám két valós számból álló pár, két komplex szám megegyezik, ha a komponenseik megegyeznek, összeadni komponensenként kell, a szorzás jóval bonyolultabb, az 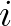 az a szám, amelyben az első komponens 0, a második 1, és így tovább. A másik kurzuson Bessel professzor elmondta, hogy egy komplex szám két valós szám, amelyek közül az első nemnegatív, két komplex szám megegyezik, ha az első komponensük nulla, vagy az első komponensük megegyezik és a második komponensük
az a szám, amelyben az első komponens 0, a második 1, és így tovább. A másik kurzuson Bessel professzor elmondta, hogy egy komplex szám két valós szám, amelyek közül az első nemnegatív, két komplex szám megegyezik, ha az első komponensük nulla, vagy az első komponensük megegyezik és a második komponensük 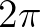 többszörösével tér el egymástól, az összeadás nehezebb, a szorzás egyszerű, és így tovább. A második óra előtt egy adminisztratív hiba következtében felcserélték a két termet, így innentől Bessel Descartes hallgatóit tanította és fordítva. Lement a szemeszter, és csodák csodájára sem Bessel, sem Descartes nem követett el erkölcsi turpisságot, pedig a másik definíciója alapján ítélték meg őket. A második órától mindkét professzor intuitívan a komplex számok absztrakt típusával dolgozott, és nem használt reprezentáció-függő tulajdonságokat. A tanulság: a típusok absztrakciót tesznek lehetővé.”
többszörösével tér el egymástól, az összeadás nehezebb, a szorzás egyszerű, és így tovább. A második óra előtt egy adminisztratív hiba következtében felcserélték a két termet, így innentől Bessel Descartes hallgatóit tanította és fordítva. Lement a szemeszter, és csodák csodájára sem Bessel, sem Descartes nem követett el erkölcsi turpisságot, pedig a másik definíciója alapján ítélték meg őket. A második órától mindkét professzor intuitívan a komplex számok absztrakt típusával dolgozott, és nem használt reprezentáció-függő tulajdonságokat. A tanulság: a típusok absztrakciót tesznek lehetővé.”
A reprezentáció-függetlenség elvének egyik lehetséges megadása a következő: ha két típus között bijekció van, általánosabban, ha két struktúra izomorf, akkor nem lehet őket megkülönböztetni. Ez az elv teljesül a típuselméletben, de a halmazelméletben nem: például 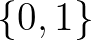 és
és 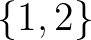 között van bijekció, mégis megkülönböztethetők: az előbbire teljesül, hogy benne van a 0, az utóbbira nem. A reprezentáció-függetlenséget a típuselmélet úgy éri el, hogy bizonyos dolgokról nem lehet beszélni: nincs unió, metszet,
között van bijekció, mégis megkülönböztethetők: az előbbire teljesül, hogy benne van a 0, az utóbbira nem. A reprezentáció-függetlenséget a típuselmélet úgy éri el, hogy bizonyos dolgokról nem lehet beszélni: nincs unió, metszet, 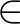 (eleme) reláció, amelyekkel a reprezentáció feltárulna. (Talán meglepő lehet, hogy egy ilyen korlátozott nyelvben is leírható a matematika, de a tapasztalat [18] azt mutatja, hogy ez a korlátozás nem hogy nehezíti, hanem könnyíti a dolgunkat). A halmezelmélet elsőrendű logikai elmélet. Ez azt jelenti, hogy a halmazelmélet formális nyelve tárgyakról (halmazokról) beszél, illetve ilyen felett képes kvantifikálni, azaz megvannak benne a „minden halmazra igaz, hogy...” és a „létezik olyan halmaz, amelyre igaz hogy...” alakú mondatok. A típuselmélet nem az elsőrendű logika egy nyelve, hanem egy önálló formális rendszer, tartalmazza a logikát is és a típusokat is, beleértve ebbe a függvénytípust is. Míg a halmazelméletben a
(eleme) reláció, amelyekkel a reprezentáció feltárulna. (Talán meglepő lehet, hogy egy ilyen korlátozott nyelvben is leírható a matematika, de a tapasztalat [18] azt mutatja, hogy ez a korlátozás nem hogy nehezíti, hanem könnyíti a dolgunkat). A halmezelmélet elsőrendű logikai elmélet. Ez azt jelenti, hogy a halmazelmélet formális nyelve tárgyakról (halmazokról) beszél, illetve ilyen felett képes kvantifikálni, azaz megvannak benne a „minden halmazra igaz, hogy...” és a „létezik olyan halmaz, amelyre igaz hogy...” alakú mondatok. A típuselmélet nem az elsőrendű logika egy nyelve, hanem egy önálló formális rendszer, tartalmazza a logikát is és a típusokat is, beleértve ebbe a függvénytípust is. Míg a halmazelméletben a 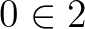 egy állítás (amely történetesen megkülönbözteti Zermelo és von Neumann implementációit), addig a típuselméletben a
egy állítás (amely történetesen megkülönbözteti Zermelo és von Neumann implementációit), addig a típuselméletben a 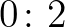 szimbólumsorozat nyelvtanilag értelmetlen, nem is lehet kimondani. A halmazelméletben is vannak nyelvtanilag értelmetlen szimbólumsorozatok, ilyen például az
szimbólumsorozat nyelvtanilag értelmetlen, nem is lehet kimondani. A halmazelméletben is vannak nyelvtanilag értelmetlen szimbólumsorozatok, ilyen például az 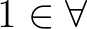 . A típuselméleti
. A típuselméleti 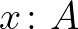 nem állítás, hanem ítélet, ahhoz hasonló, mint az elsőrendű logika bizonyításelméletében a „
nem állítás, hanem ítélet, ahhoz hasonló, mint az elsőrendű logika bizonyításelméletében a „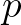 bizonyítja
bizonyítja  -t” ítélet. Informatikai analógiával a halmazelméleti
-t” ítélet. Informatikai analógiával a halmazelméleti 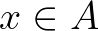 dinamikus információt fejez ki (lehet bizonyítani), míg a típuselméleti
dinamikus információt fejez ki (lehet bizonyítani), míg a típuselméleti 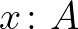 statikus: minden termhez (elemhez) elválaszthatatlanul hozzártartozik a típusa, és az nem változtatható meg. Nem lehet például egy
statikus: minden termhez (elemhez) elválaszthatatlanul hozzártartozik a típusa, és az nem változtatható meg. Nem lehet például egy 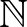 típusú (természetes szám típusú) termet
típusú (természetes szám típusú) termet 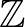 típusúnak (egész szám típusúnak) is tekinteni. Megadható ugyan egy természetes injektív
típusúnak (egész szám típusúnak) is tekinteni. Megadható ugyan egy természetes injektív 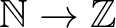 típusú függvény és ez beágyazza az első típust a másikba, de ettől a természetes szám típusú entitások nem lesznek egész típusú entitások is.
típusú függvény és ez beágyazza az első típust a másikba, de ettől a természetes szám típusú entitások nem lesznek egész típusú entitások is.
Míg a halmazelmélet a logikára épül, elsőrendű logikai módon írjuk le, hogyan tudunk halmazokat megadni (pl. a részhalmaz-axiómával), addig a típuselméletben a típusok (gyűjtemények) az elsődlegesek, és a logikai állításokat, logikai operátorokat típusokkal kódoljuk. A 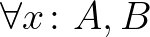 nem egy állítás, hanem egy típus, éspedig egy függő függvényípus: ha
nem egy állítás, hanem egy típus, éspedig egy függő függvényípus: ha 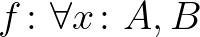 , akkor
, akkor 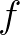 olyan függvény, amely tetszőleges
olyan függvény, amely tetszőleges  típusú
típusú 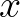 -hez egy akár
-hez egy akár 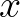 -től is függő
-től is függő 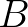 típusú dolgot rendel. A típusok tehát nemcsak olyan dolgok, amin a hagyományos matematikában „halmaz”-t értenénk, hanem olyan dolgok is tudnak lenni, amik a hagyományos matematikában az „állítások” szerepét töltenék be. Nem kell az időzőjeleken meglepődni: a típuselmélet a matematikai valóság alternatív felépítése, a halmazelméleti kifejezések csak hasonlóságra utalnak. Viszont ha borzasztóan vágyunk rá, akkor megtalálhatjuk az állításokat a típuselméletben is. Típuselméleti értelemben egy
típusú dolgot rendel. A típusok tehát nemcsak olyan dolgok, amin a hagyományos matematikában „halmaz”-t értenénk, hanem olyan dolgok is tudnak lenni, amik a hagyományos matematikában az „állítások” szerepét töltenék be. Nem kell az időzőjeleken meglepődni: a típuselmélet a matematikai valóság alternatív felépítése, a halmazelméleti kifejezések csak hasonlóságra utalnak. Viszont ha borzasztóan vágyunk rá, akkor megtalálhatjuk az állításokat a típuselméletben is. Típuselméleti értelemben egy  típus állítás, ha legfeljebb egy olyan
típus állítás, ha legfeljebb egy olyan 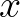 van, ami
van, ami  típusú. Egy bizonyítás pedig a megfelelő (állítás-)típus eleme. Ez az egyszerű állítás-definíció viszonylag friss (Voevodsky adta meg 2010 körül), de jól illeszkedik az általában állításnak nevezett dolgokhoz: az állítás bizonyítása nem érdekes, ha már tudjuk, hogy van bizonyítás, elfelejthetjük, hogy az pontosan hogyan készült, nem tudunk információt kinyerni belőle. A relációk/részhalmazok a karakterisztikus függvényükkel vannak megadva: egy
típusú. Egy bizonyítás pedig a megfelelő (állítás-)típus eleme. Ez az egyszerű állítás-definíció viszonylag friss (Voevodsky adta meg 2010 körül), de jól illeszkedik az általában állításnak nevezett dolgokhoz: az állítás bizonyítása nem érdekes, ha már tudjuk, hogy van bizonyítás, elfelejthetjük, hogy az pontosan hogyan készült, nem tudunk információt kinyerni belőle. A relációk/részhalmazok a karakterisztikus függvényükkel vannak megadva: egy 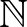 feletti predikátum (unáris reláció) egy
feletti predikátum (unáris reláció) egy 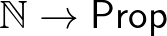 függvény, ahol a
függvény, ahol a 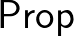 az állítás-típusok típusa.
az állítás-típusok típusa.
Néhány példa a logikai operátorok kódolására: a konjunkció (és) a szorzat típussal van megadva (ami a halmazok Descartes-szorzatát is kódolja), a 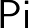 típus pedig reprezentálhat általánosított Descartes-szorzatot, függvénytípust, univerzális kvantort és implikációt is. Nemsokára megmutatjuk, hogy ez pontosan hogyan történik.
típus pedig reprezentálhat általánosított Descartes-szorzatot, függvénytípust, univerzális kvantort és implikációt is. Nemsokára megmutatjuk, hogy ez pontosan hogyan történik.
Ahol veszítesz, ott nyersz
A típuselmélet alkalmas a matematika konstruktív felépítésére. A konstruktivitás nem fosztóképző, hanem annak ellentéte: a típuselmélet általánosabb elmélet, mint a halmazelmélet, hiszen nem zárjuk ki a harmadik esetet (nem követeljük meg a kizárt harmadik elvét). A halmazelmélet mögötti logikában megköveteljük azt, hogy egy állítás és tagadása közül legalább az egyik legyen igaz. Az ilyen logikát klasszikusnak nevezzük. A típuselméletben tudunk klasszikusan is és konstruktívan is bizonyítani, de az utóbbi bizonyítások automatikusan (számítógéppel) végrehajtható programok lesznek. Például, ha típuselméletben bebizonyítjuk (a kizárt harmadik elvének illetve a kiválasztási axiómának felhasználása nélkül), hogy bármely két természetes számnak van legnagyobb közös osztója, akkor az a bizonyítás valójában program, amelynek bemenete két szám, kimenete pedig szintén két dolog: egy szám és annak az állításnak a bizonyítása, hogy a kimeneti szám a két bemenet legnagyobb közös osztója. A típuselmélet nem axiomatikus felépítésű: a típuselmélet programozási nyelv, a különböző típusokra vonatkozó szabályok mind úgy vannak megadva, hogy végrehajthatók legyenek. A típuselmélet nem Turing-teljes, ez azt jelenti, hogy nem minden kiszámítható függvény írható le benne (például nem tudunk típuselmélet-kiértékelőt írni típuselméletben, csak eggyel „kisebb” típuselméletre; hiszen ekkor a típuselmélet be tudná látni önmaga konzisztenciáját, ami Gödel miatt nem lehetséges). Bármilyen bonyolultan is adjuk meg a legnagyobb közös osztós bizonyítást, az mindig véges időn belül végrehajtható lesz számítógéppel (persze, attól függően, hogyan adtuk meg, lehet hatékony/gyors vagy nem-hatékony/lassú). A kizárt harmadik elvének és a kiválasztási axiómának nincs komputációs jelentése. Ha a bizonyítás ezen elvek valamelyikét használja, akkor annak programként való végrehajtása az adott axiómára hivatkozásnál elakad: a program végrehajtása megszakad, és például nem kapunk eredményként egy konkrét számot (nullát, egyet, kettőt stb.), hanem csak egy bonyolult megadású 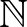 típusú termet. De senki nem akadályozza meg a bizonyítás-ellenőrző felhasználóját, hogy ilyen elveket is feltételezve végezze a bizonyításokat: a Lean Mathlib-ben [18] az egyetemi matematika tananyagot például teljesen klasszikusan formalizálták.
típusú termet. De senki nem akadályozza meg a bizonyítás-ellenőrző felhasználóját, hogy ilyen elveket is feltételezve végezze a bizonyításokat: a Lean Mathlib-ben [18] az egyetemi matematika tananyagot például teljesen klasszikusan formalizálták.
De még ha gyakran is alkalmazunk klasszikus elveket a bizonyításokban, nagyon hasznos, hogy programozni is tudunk: például annak bizonyítása, hogy 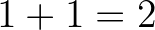 pontosan ugyanaz, mint annak, hogy
pontosan ugyanaz, mint annak, hogy 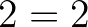 . Ez azért van, mert az összeadás egy
. Ez azért van, mert az összeadás egy 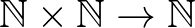 típusú program (megadásakor nincs szükségünk axiómák használatára), amely az 1 és 1 bemeneteken elindítva 2-t ad. Ezt úgy nevezzük, hogy számítással bizonyítunk. Ha van két bonyolult konstrukció, amelyek egyenlőségét szeretnénk bizonyítani, gyakran csak végre kell hajtanunk a két programot, az eredmények már meg is egyeznek, és a bizonyítás egyszerűen az egyenlőség reflexivitási tulajdonságára való hivatkozás lesz. A programok végrehajtása és a definíciók feloldása automatikusan megtörténik típusellenőrzés/bizonyításellenőrzés során. Halmazelméletben a függvények relációk, amelyeket csak „kézzel” tudunk végrehajtani, tehát voltaképpen nem tudjuk őket számítógéppel lefuttatni.
típusú program (megadásakor nincs szükségünk axiómák használatára), amely az 1 és 1 bemeneteken elindítva 2-t ad. Ezt úgy nevezzük, hogy számítással bizonyítunk. Ha van két bonyolult konstrukció, amelyek egyenlőségét szeretnénk bizonyítani, gyakran csak végre kell hajtanunk a két programot, az eredmények már meg is egyeznek, és a bizonyítás egyszerűen az egyenlőség reflexivitási tulajdonságára való hivatkozás lesz. A programok végrehajtása és a definíciók feloldása automatikusan megtörténik típusellenőrzés/bizonyításellenőrzés során. Halmazelméletben a függvények relációk, amelyeket csak „kézzel” tudunk végrehajtani, tehát voltaképpen nem tudjuk őket számítógéppel lefuttatni.
Kapcsolódó kérdés, hogy a matematika mely részei építhetők fel teljesen konstruktívan. A Feith–Thompson-tétel (minden páratlan rendű véges csoport feloldható) bizonyítását például teljesen konstruktívan formalizálták Coq-ban [7]. Az analízis híresen nem-konstruktív, ez volt Hilbert egyik fő ellenérve a Brouwerrel folytatott vitájában. Hilbert sokat idézett mondata is erre vonatkozik: a matematikusnak megtiltani a kizárt harmadik elve haszálatát olyan, mint az ökölvívónak megtiltani, hogy használja az öklét. [8, 476] És valóban, Brouwer intuicionista analízisében például minden függvény folytonos, amely tény méltán borzolhatja a klasszikus matematikusok kedélyeit. Hilbert halála után 24 évvel Errett Bishop megmutatta, hogy Hilbertnek olyan éles értelemben, ahogy fogalmazott, nem volt igaza [4]: ha elég óvatosan dolgozunk, az analízisnek egy legalább olyan értékes és alkalmazható formája felépíthető teljes egészében a kizárt harmadik elve és a kiválasztási axióma használata nélkül, mint klasszikus ellenpárja. Az óvatosságra egy példa: azt, hogy egy függvény injektív, nem úgy mondjuk ki, hogy két különböző bemenetet nem küld ugyanarra a kimenetre, hanem úgy, hogy ha 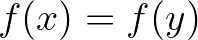 , akkor
, akkor 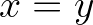 . Míg a kizárt harmadik elve feltételezésével a két definíció megegyezik, konstruktív közegben az utóbbi erősebb. Még egy példa: egy gondosan felépített konstruktív analízisben a Bolzano-tétel klasszikus formájára voltaképpen nincs is szükség (ha egy intervallumon folytonos függvénynek van negatív és pozitív értéke is, akkor van zérushelye). A konstruktív matematikában, például a mérnöki alkalmazások szempontjából, elég egy olyan alak, amelyben a szóban forgó függvény felvesz nullához tetszőlegesen közeli értéket. Bishop könyve azonban nagyon nehezen olvasható. Úgy is mondhatjuk, hogy a Bishop-stílusú analízis csúnya: a kiválasztási axióma elkerülése érdekében reprezentációkkal dolgozik. A valós számokat Cauchy-sorozatok kvóciensei helyett magukkal a sorozatokkal adja meg, ezért a felépítésének „gépi kódú” programozás íze van. A probléma az, hogy a kvóciensezett Cauchy-sorozatok Cauchy-teljességének bizonyításához szükségünk van a kiválasztási axiómára. 2012-ig kellett várni, mire kiderült, hogy óvatosabban megadva a Cauchy-sorozatokat ez a nehézség elkerülhető [22, 11. fej]. Az alapötlet, hogy a kvócienst nem utólag kell venni, hanem a sorozat megadásával egyszerre kell elkészíteni. Hogy egyszerre konstruktívan és magas absztrakciós szinten (szépen) felépíthető-e az analízis, azt nem tudjuk, mert azt még senki sem próbálta ki.
. Míg a kizárt harmadik elve feltételezésével a két definíció megegyezik, konstruktív közegben az utóbbi erősebb. Még egy példa: egy gondosan felépített konstruktív analízisben a Bolzano-tétel klasszikus formájára voltaképpen nincs is szükség (ha egy intervallumon folytonos függvénynek van negatív és pozitív értéke is, akkor van zérushelye). A konstruktív matematikában, például a mérnöki alkalmazások szempontjából, elég egy olyan alak, amelyben a szóban forgó függvény felvesz nullához tetszőlegesen közeli értéket. Bishop könyve azonban nagyon nehezen olvasható. Úgy is mondhatjuk, hogy a Bishop-stílusú analízis csúnya: a kiválasztási axióma elkerülése érdekében reprezentációkkal dolgozik. A valós számokat Cauchy-sorozatok kvóciensei helyett magukkal a sorozatokkal adja meg, ezért a felépítésének „gépi kódú” programozás íze van. A probléma az, hogy a kvóciensezett Cauchy-sorozatok Cauchy-teljességének bizonyításához szükségünk van a kiválasztási axiómára. 2012-ig kellett várni, mire kiderült, hogy óvatosabban megadva a Cauchy-sorozatokat ez a nehézség elkerülhető [22, 11. fej]. Az alapötlet, hogy a kvócienst nem utólag kell venni, hanem a sorozat megadásával egyszerre kell elkészíteni. Hogy egyszerre konstruktívan és magas absztrakciós szinten (szépen) felépíthető-e az analízis, azt nem tudjuk, mert azt még senki sem próbálta ki.
A konstruktivitás iránt érdeklődőknek ajánljuk Andrej Bauer cikkét a konstruktív matematika elfogadásának öt szakaszáról. Igen: itt a gyászfeldolgozás öt szakaszáról van szó [2].
Egyenlőség, extenzionalitás.
A típuselmélet egy érdekes sajátossága, hogy egy 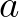 dolog, ami egy
dolog, ami egy  típus eleme, nem tud egy másik
típus eleme, nem tud egy másik 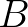 típusnak is eleme lenni, pont úgy, ahogy egy tégla se tud egyszerre két különböző háznak téglája lenni. Ezért van, hogy a típuselméletben inkább el is kerülik az „elem” és „eleme” kifejezéseket. Elem helyett termet (a terminus, kifejezés értelmében) vagy lakót mondanak, az eleme reláció helyett pedig azt mondják, hogy az
típusnak is eleme lenni, pont úgy, ahogy egy tégla se tud egyszerre két különböző háznak téglája lenni. Ezért van, hogy a típuselméletben inkább el is kerülik az „elem” és „eleme” kifejezéseket. Elem helyett termet (a terminus, kifejezés értelmében) vagy lakót mondanak, az eleme reláció helyett pedig azt mondják, hogy az 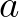 lakója az
lakója az  típusnak vagy egyszerűen, hogy az
típusnak vagy egyszerűen, hogy az 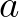 egy
egy  típusú term (jelben, ahogy korábban is írtuk:
típusú term (jelben, ahogy korábban is írtuk: 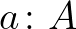 ).
).
Egy másik nagyon jelentős eltérés a klasszikus felépítéshez képest, hogy az egyenlőség – ahogy korábban említettük – nem logikai reláció, hanem maga is egy típus, amelynek lakói vannak, olyan entitások, amelyek igazolják az egyenlőség fennállását. A halmazelméletben az extenzionalitás axiómája azt mondja ki, hogy ha két halmaznak ugyanazok az elemei, akkor egyenlők. A típuselméletben ez az axióma az előbbiek miatt értelmetlen, nem tudjuk két különböző típus elemeit összehasonlítani. Reprezentáció-független viszonyok között máshogy fogalmazzuk meg az extenzionalitást: azt mondjuk, hogy ha két típus között van bijekció, akkor egyenlők. A precízebb megfogalmazás Voevodsky univalencia axiómája [22, 2.10. fej]: a típusok egyenlőségét az ekvivalenciába képző függvény egy ekvivalencia; a univelance fontos előzménye volt a típuselmélet groupoid modellje [9] és Makkai Mihály FOLDS rendszere [15,16].
A típusok egyenlőségét bijekciónak venni messzemenő következményekkel jár: az egyenlőség már nem mindig állítás, tehát két dolog lehet többféleképpen is egyenlő. Ez nem változtat az úgynevezett halmazok egyenlőségén: a típuselméletben egy olyan  típust nevezünk halmaznak, amelynek egyenlőségei állítások, tehát
típust nevezünk halmaznak, amelynek egyenlőségei állítások, tehát 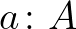 és
és 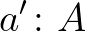 esetén az
esetén az 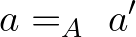 típusnak (amely
típusnak (amely 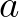 és
és 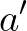 egyenlőségét fejezi ki) vagy nincs eleme vagy csak egy eleme van. Halmazok esetén az ekvivalencia bijekciót jelent. Halmazok például az
egyenlőségét fejezi ki) vagy nincs eleme vagy csak egy eleme van. Halmazok esetén az ekvivalencia bijekciót jelent. Halmazok például az 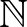 ,
, 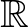 ,
, 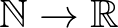 ,
, 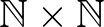 típusok, vagyis
típusok, vagyis 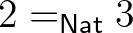 állítás,
állítás, 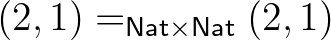 állítás,
állítás, 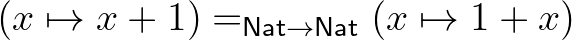 állítás. De a típusok egyenlősége már nem állítás: például a kételemű (Bool) típust
állítás. De a típusok egyenlősége már nem állítás: például a kételemű (Bool) típust 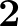 -vel jelölve a
-vel jelölve a 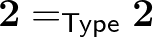 egy eleme az univalencia miatt ugyanaz, mint egy
egy eleme az univalencia miatt ugyanaz, mint egy 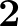 és
és 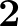 közötti bijekció, ilyenből pedig kettő van: az identitás és a tagadás (csere).
közötti bijekció, ilyenből pedig kettő van: az identitás és a tagadás (csere).
Az univalencia axiómát a típuselmélet homotopikus modelljei [13,3] inspirálták: ezekben a modellekben a típusok absztrakt (geometriai) terek, a termek a tér pontjai, az egyenlőség típust pedig a térben lévő utak adják meg (alkotják). Ilyen absztrakt terek a szimpliciális vagy a kubikális halmazok. Az univalenciával eredetileg ugyanaz volt a probléma, mint a kizárt harmadik elvével: axióma, tehát nem tudjuk, hogyan kell vele számolni, nincs komputációs tartalma. Coquand és munkatársai kifejlesztették a kubikális típuselméletet [6], amelyben az univalencia bizonyítható, nem szükséges axiómaként hozzávenni a rendszerhez. A kubikális típuselmélet azonban bonyolult (a szabályok megértéséhez szükséges a magasabbdimenziós absztrakt terek ismerete), implementációi (pl. Cubical Agda) lassúak, és az  és az
és az  és
és 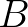 közötti ekvivalencia közötti megfelelés gyenge. Van tehát még tér a fejlesztésre: a Higher Observational Type Theory ERC projekt [1] célja egy olyan új típuselmélet kifejlesztése, amely ezeket a problémákat orvosolja.
közötti ekvivalencia közötti megfelelés gyenge. Van tehát még tér a fejlesztésre: a Higher Observational Type Theory ERC projekt [1] célja egy olyan új típuselmélet kifejlesztése, amely ezeket a problémákat orvosolja.
Bepiszkoljuk a kezünket?
Most megadunk teljesen precízen egy típuselméletet minimális mennyiségű szabállyal, és ízelítőként mutatunk néhány egyszerű definíciót, bizonyítást. Vigyázat, öveket bekötni!
Ha van egy 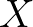 halmazunk és egy
halmazunk és egy 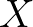 elemeivel indexelt
elemeivel indexelt 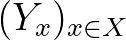 halmazcsaládunk, akkor az
halmazcsaládunk, akkor az 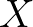 -szeres Descartes szorzatot
-szeres Descartes szorzatot 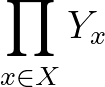 -szel jelöljük. Ennek elemei olyan
-szel jelöljük. Ennek elemei olyan 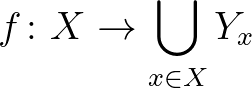 függvények, amelyekre
függvények, amelyekre 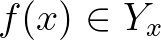 teljesül. Például ha
teljesül. Például ha 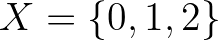 és
és 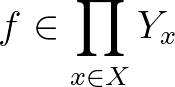 , akkor
, akkor 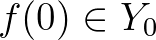 ,
, 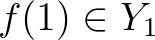 ,
, 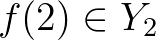 . Ennek duálisa az
. Ennek duálisa az 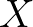 -szeres diszjunkt unió
-szeres diszjunkt unió 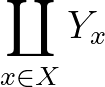 , amelynek elemei
, amelynek elemei 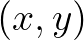 párok, ahol
párok, ahol 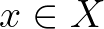 és
és 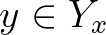 .
.
Feltételezünk egy halmazt, amelyet 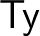 -nak nevezünk, elemeit típusoknak hívjuk. Minden
-nak nevezünk, elemeit típusoknak hívjuk. Minden 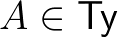 -hoz adott egy
-hoz adott egy 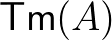 halmaz, amelynek elemeit
halmaz, amelynek elemeit  típusú termeknek nevezzük. Továbbá adottnak vesszük az alábbi halmaz-elemeket, függvényeket és egyenlőségeket:
típusú termeknek nevezzük. Továbbá adottnak vesszük az alábbi halmaz-elemeket, függvényeket és egyenlőségeket:
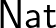 |
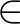 |
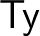 |
(1) | ||||
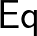 |
: | 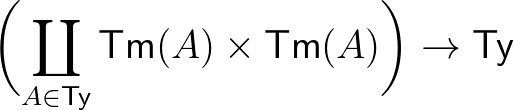 |
(2) | ||||
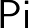 |
: | 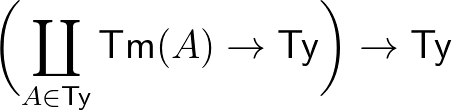 |
(3) | ||||
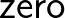 |
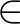 |
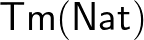 |
(4) | ||||
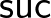 |
: |  |
(5) | ||||
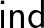 |
: | 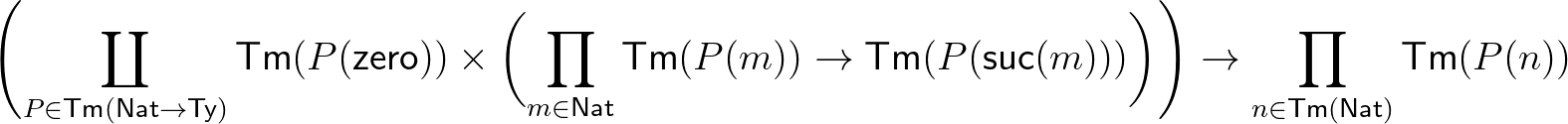 |
(6) | ||||
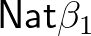 azt állítja, hogy minden azt állítja, hogy minden 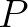 , , 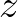 , , 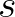 -re -re 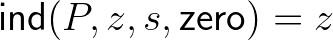 . . |
(7) | ||||||
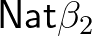 azt állítja, hogy minden azt állítja, hogy minden 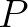 , , 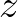 , , 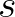 , , 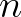 -re -re 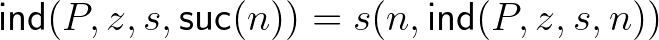 . . |
(8) | ||||||
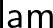 |
: | 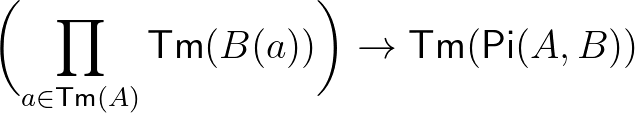 minden minden  , , 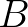 -re -re |
(9) | ||||
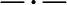 |
: | 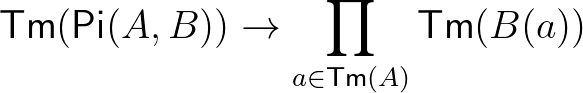 minden minden  , , 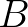 -re -re |
(10) | ||||
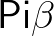 azt állítja, hogy minden azt állítja, hogy minden  , , 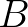 , , 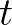 , , 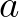 -ra -ra 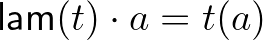 . . |
(11) | ||||||
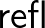 |
: | 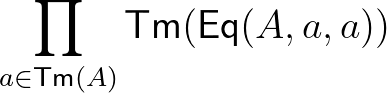 minden minden  -ra -ra |
(12) | ||||
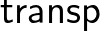 |
: | 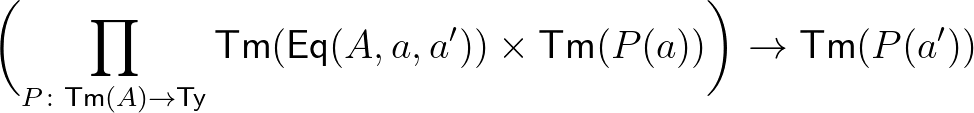 minden minden  -ra -ra |
(13) | ||||
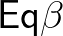 azt állítja, hogy minden azt állítja, hogy minden  , , 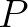 , , 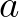 , , 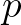 -re -re 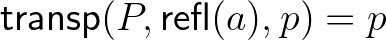 . . |
(14) | ||||||
A fenti definíció egy programozási nyelv [11,12]: feltételezve a fenti halmazokat, függvényeket és egyenlőségeket, amit ezekből kombinálva létre tudunk hozni, azok a típusok és az adott típusú programok (termek); ha két termről az egyenlőségeket kombinálva be tudjuk látni, hogy egyenlők, az azt jelenti, hogy programként végrehajtva ugyanaz az eredményük. A fenti programozási nyelv egy implementációja az egyenlőségek mentén addig alakítja a termeket, amíg már nem lehet tovább egyszerűsíteni őket. Ezt normalizálásnak nevezik és voltaképpen a programfuttatásnak felel meg, illetve a lefutott programból a végeredmény kinyerésének.
Most soronként elmagyarázzuk, hogy a programozási nyelv komponensei mire valók, majd írunk néhány példát, hogy a fenti komponensekből hogyan tudunk típusokat, termeket, programokat, állításokat és bizonyításokat összerakni.
Háromféle módon tudunk típust létrehozni: (1) egyrészt van a természetes számoknak egy 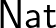 típusa, (2) másrészt bármely
típusa, (2) másrészt bármely  típusra és két
típusra és két  típusú
típusú 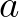 ,
, 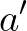 termre van egy
termre van egy 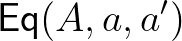 egyenlőség típus, amit
egyenlőség típus, amit 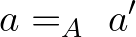 -nek is szoktunk írni. (3) Harmadrészt van
-nek is szoktunk írni. (3) Harmadrészt van 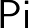 , amely egy másodrendű függvény: bemenete egy típus és egy ilyen típusú termből
, amely egy másodrendű függvény: bemenete egy típus és egy ilyen típusú termből 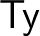 -ba képező függvény, kimenete egy típus.
-ba képező függvény, kimenete egy típus. 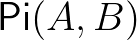 az
az  -ból
-ból 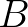 -be képező függő függvény típus. Mint fentebb említettük,
-be képező függő függvény típus. Mint fentebb említettük, 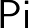 -vel kódoljuk a halmazelméletben előforduló alábbi négy fogalmat:
-vel kódoljuk a halmazelméletben előforduló alábbi négy fogalmat:
 Ha van egy
Ha van egy 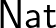 elemeivel indexelt típuscsalád, tehát egy
elemeivel indexelt típuscsalád, tehát egy 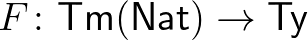 függény, akkor az
függény, akkor az 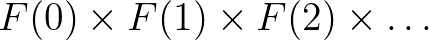 végtelen Descartes-szorzatot
végtelen Descartes-szorzatot 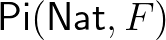 -fel jelöljük.
-fel jelöljük.
 A
A 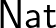 -ből
-ből 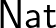 -be képező függvények típusa
-be képező függvények típusa 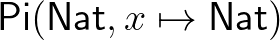 , ahol az
, ahol az  a konstans
a konstans 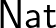 függvény. Általánosan, ha
függvény. Általánosan, ha 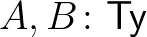 , a közöttük lévő nem-függő függvény típust az
, a közöttük lévő nem-függő függvény típust az  rövidítéssel adjuk meg. Schönfinkel (curry-zésnek nevezett) módszerével meg tudunk adni többparaméteres függény típust is, például az összeadás típusa
rövidítéssel adjuk meg. Schönfinkel (curry-zésnek nevezett) módszerével meg tudunk adni többparaméteres függény típust is, például az összeadás típusa 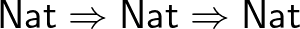 , ahol a
, ahol a 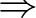 operátor jobbra zárójeleződik.
operátor jobbra zárójeleződik.
 A következő típus azt fejezi ki, hogy az egyenlőség reflexív:
A következő típus azt fejezi ki, hogy az egyenlőség reflexív: 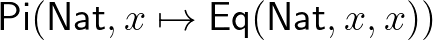 . Ezt úgy olvassuk, hogy minden
. Ezt úgy olvassuk, hogy minden 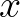 természetes számra
természetes számra 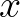 egyenlő
egyenlő 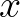 -szel. Egy
-szel. Egy 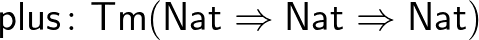 termmel megadott összeadás művelet kommutativitását a következőképp fejezzük ki:
termmel megadott összeadás művelet kommutativitását a következőképp fejezzük ki: 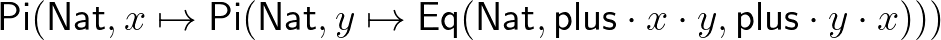 . A következő típus azt fejezi ki, hogy a természetes számok típusa halmaz (típuselméleti értelemben):
. A következő típus azt fejezi ki, hogy a természetes számok típusa halmaz (típuselméleti értelemben):

 Ha
Ha  és
és 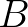 állítások (típuselméleti értelemben), akkor az
állítások (típuselméleti értelemben), akkor az  típus szintén állítás, és azt fejezi ki, hogy
típus szintén állítás, és azt fejezi ki, hogy  -ból következik
-ból következik 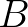 .
.
A természetes számoknak két úgynevezett konstruktora van, (4) nulla és (5) rákövetkező, például 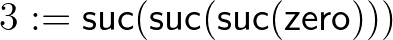 . A (6) destruktor (eliminátor, iterátor, rekurzor, fold operátor, indukciós elv) azt mondja, hogy ha adott egy
. A (6) destruktor (eliminátor, iterátor, rekurzor, fold operátor, indukciós elv) azt mondja, hogy ha adott egy 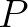 típuscsalád (például egy predikátum), amely teljesül
típuscsalád (például egy predikátum), amely teljesül 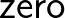 -ra és ha teljesül
-ra és ha teljesül 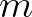 -re, akkor
-re, akkor 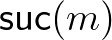 -re is, akkor minden
-re is, akkor minden 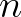 -re teljesül. A természetes számok konstruktorai és destruktora harmóniában vannak: ezt fejezi ki (7)–(8) a két
-re teljesül. A természetes számok konstruktorai és destruktora harmóniában vannak: ezt fejezi ki (7)–(8) a két 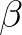 egyenlőség: ezek elmondják, hogyan kell a destruktor alkalmazását kiszámítani. A destruktor nem csak a szokásos teljes indukció elvét implementálja, hanem segítségével tudunk
egyenlőség: ezek elmondják, hogyan kell a destruktor alkalmazását kiszámítani. A destruktor nem csak a szokásos teljes indukció elvét implementálja, hanem segítségével tudunk 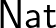 -ból kifelé menő függvényeket megadni.
-ból kifelé menő függvényeket megadni.
(9) Függvény típusú termeket a 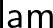 művelettel tudunk megadni, amely a
művelettel tudunk megadni, amely a 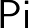 -hez hasonlóan másodrendű függvény:
-hez hasonlóan másodrendű függvény: 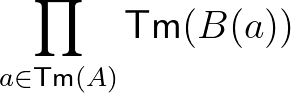 -ből képez
-ből képez 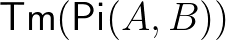 -be, tetszőleges
-be, tetszőleges  ,
, 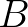 -re (amelyeket nem írunk ki az olvashatóság kedvéért). Például a konstans nulla függvényt a
-re (amelyeket nem írunk ki az olvashatóság kedvéért). Például a konstans nulla függvényt a  term adja meg. Az (10)
term adja meg. Az (10) 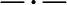 applikáció a
applikáció a 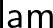 ellentéte, amellyel egy függvény típusú termet tudunk egy bemenetre alkalmazni. Infix módon írjuk (mint az összeadást szoktuk). (11) A
ellentéte, amellyel egy függvény típusú termet tudunk egy bemenetre alkalmazni. Infix módon írjuk (mint az összeadást szoktuk). (11) A 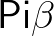 a függvény típus számítási szabálya, elmagyarázza, hogyan kell
a függvény típus számítási szabálya, elmagyarázza, hogyan kell 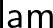 -mal készített termet bemenetre alkalmazni.
-mal készített termet bemenetre alkalmazni.
(12) Az egyenlőség típusnak egy konstruktora van, a reflexivitás, (13) destruktora pedig a Leibniz-szabály: ha 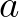 egyenlő
egyenlő 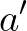 -vel, akkor
-vel, akkor 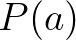 -ból következik
-ból következik 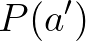 . (14) Ezek harmóniája azt jelenti, hogy a Leibniz-szabály a reflexivitásra alkalmazva az identitás függvény.
. (14) Ezek harmóniája azt jelenti, hogy a Leibniz-szabály a reflexivitásra alkalmazva az identitás függvény.
Egy szám megelőzőjét kiszámító termet a következőképp adunk meg:
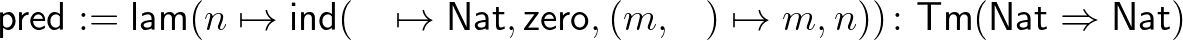
Ezt úgy olvassuk, hogy megadunk egy függvényt ( 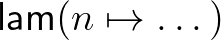 ), amely a bemenetén indukciót csinál (amely most csak egy esetszétválasztás), 0 esetén 0-t ad vissza, ha egy szám
), amely a bemenetén indukciót csinál (amely most csak egy esetszétválasztás), 0 esetén 0-t ad vissza, ha egy szám 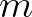 rákövetkezője, akkor pedig
rákövetkezője, akkor pedig 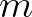 -et ad vissza. Például a megelőzőt 2-re alkalmazva a következő módon számolunk:
-et ad vissza. Például a megelőzőt 2-re alkalmazva a következő módon számolunk:
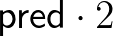 |
 |
(rövidítés) | ||
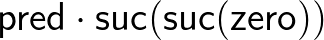 |
 |
(rövidítés) | ||
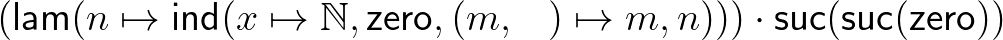 |
 |
(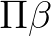 ) ) |
||
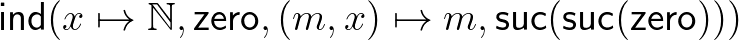 |
 |
( 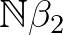 ) ) |
||
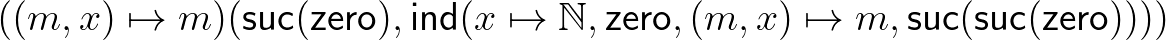 |
 |
(rövidítés) | ||
 |
 |
(rövidítés) | ||
| 1 |
A fenti egyenlőségláncolat, mint érvelés, automatikus lefuttatását ennek a típuselméletnek egy alkalmas és problémamentesen kivitelezhető számítógépes implementációja elvégzi helyettünk, és ha a 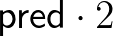 programot futtatjuk, végeredményként megkapjuk az 1-et.
programot futtatjuk, végeredményként megkapjuk az 1-et.
Megmutatunk még néhány érdekesebb definíciót. Az összeadást a következő term adja meg.
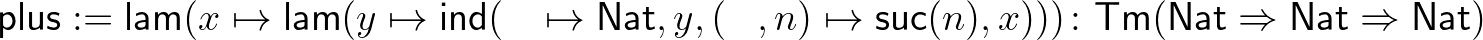
Érdemes kézzel belátni, hogy például 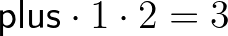 .
.
Azt, hogy 0 az összeadás bal oldali egységeleme, nagyon könnyű belátni:
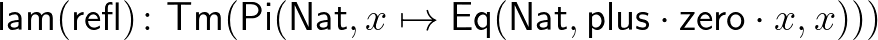
Ez azért ilyen egyszerű, mert a 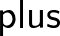 definíciója és a
definíciója és a 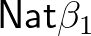 alapján
alapján 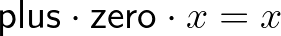 . A másik oldali egységelem-tulajdonság nehezebb: ennek bizonyításához már indukcióra van szükség, hiszen
. A másik oldali egységelem-tulajdonság nehezebb: ennek bizonyításához már indukcióra van szükség, hiszen  , amire nem tudjuk sem
, amire nem tudjuk sem 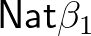 -et, sem
-et, sem 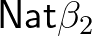 -t alkalmazni. Ezt a
-t alkalmazni. Ezt a
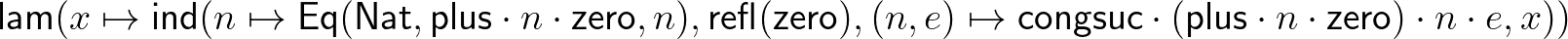
term bizonyítja, amely a 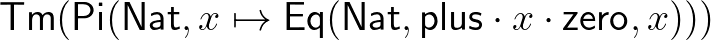 halmaz eleme. A fenti bizonyításban
halmaz eleme. A fenti bizonyításban
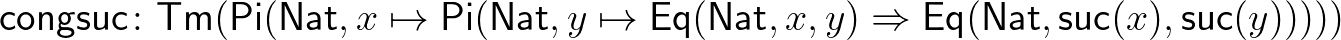
azt fejezi ki, hogy a 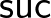 megőrzi az egyenlőséget. Bizonyítása az egyenlőség eliminátorával adható meg:
megőrzi az egyenlőséget. Bizonyítása az egyenlőség eliminátorával adható meg:
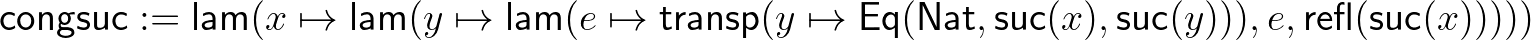
Be lehet látni – és biztatjuk is ennek elvégzésére az olvasót –, hogy a fenti egyenlőség ekvivalenciareláció, tetszőleges függvény kongruencia, definiálható a szorzás, hatványozás, és a természetes számok ezekkel a műveletekkel exponenciális félgyűrűt alkotnak.
Konklúzió
Jóllehet a halmazelmélet példásan helytáll a matematika biztos alapokra helyezésének feladatában, a matematikai fogalmak halmazelméleti formalizációjára a gyakorló matematikus csak ritka ünnepnapokon gondol. Ráadásul a bizonyítások formális leírása esetén Cantor öröksége, a halmazelméleti paradicsom, könnyen pokollá válhat. Márpedig a gyakorló matematikus számára számos okból rendkívül hasznos lehet egy automatikus érvelésellenőrző rendszer, amely éppen a formális leírásokat képes feldolgozni. Mindkét problémára megoldást kínál a típuselmélet, amely egyszerre illeszkedik természetesen a matematika strukturális világába, és képes komputációsan hatékonyan működni. Az implementációfüggetlenség természetes módon kapcsolódik a matematikus azon vágyához, hogy algebrákban, izomorf struktúrákban fogalmazza meg gondolatait, míg az axiómamentesség és a konstruktivitás funkcionális, input-output szerkezetet biztosít, így a típuselméleti formális leírásokat a számítógép gond nélkül képes végrehajtani. Még a konstruktivitás sem jelent korlátozó tényezőt, hiszen a kizárt harmadik elvének és hasonló klasszikus elveknek a típuselméletben nincs szükségszerű szerepük, legfeljebb opcionálisan alkalmazandók. Ebben az új paradicsomban, amelyet a típuselmélet teremt, a megalapozások kutatója, a gyakorló matematikus és az informatikus egyaránt otthonra lel, hiszen közös nyelvet talál a precizitás, a struktúra és a számítás világában.
Eötvös Loránd Tudományegyetem, Informatikai Kar, Programozási Nyelvek és Fordítóprogramok Tanszék
Molnár Zoltán Gábor
Budapesi Műszaki és Gazdaságtudományi Egyetem, Természettudományi Kar, Algebra és Geometria Tanszék
Hivatkozások
[1] Európa vezető felfedező kutatásai között az elte projektje, 12 2024. Közlemény az ELTE honlapján.
[2] Andrej Bauer. Five stages of accepting constructive mathematics. Bulletin of the American Mathematical Society, 54(3):481–498, 2017.
[3] Marc Bezem, Thierry Coquand, and Simon Huber. The univalence axiom in cubical sets. J. Autom. Reason., 63(2):159–171, 2019.
[4] Errett Bishop. Foundations of Constructive Analysis. Mcgraw-Hill, New York, NY, USA, 1967.
[5] Kevin Buzzard. The future of mathematics? Slides for a talk at the Colloquium Seminar of the Department of Mathematics at the University of Pittsburgh, January 2020.
[6] Cyril Cohen, Thierry Coquand, Simon Huber, and Anders Mörtberg. Cubical type theory: A constructive interpretation of the univalence axiom. In Tarmo Uustalu, editor, 21st International Conference on Types for Proofs and Programs, TYPES 2015, May 18-21, 2015, Tallinn, Estonia, volume 69 of LIPIcs, pages 5:1–5:34. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2015.
[7] Georges Gonthier. Engineering mathematics: the odd order theorem proof. In Roberto Giacobazzi and Radhia Cousot, editors, The 40th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL '13, Rome, Italy - January 23 - 25, 2013, pages 1–2. ACM, 2013.
[8] Jean Van Heijenoort, editor. From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931. Harvard University Press, Cambridge, MA, USA, 1967.
[9] Martin Hofmann and Thomas Streicher. The groupoid interpretation of type theory. In In Venice Festschrift, pages 83–111. Oxford University Press, 1996.
[10] M. Randall Holmes and Sky Wilshaw. Nf is consistent, 2024.
[11] Ambrus Kaposi. Formális nyelv = másodrendű algebrai elmélet, pages 183–218. 2024.
[12] Ambrus Kaposi and Szumi Xie. Second-order generalised algebraic theories: Signatures and first-order semantics. In Jakob Rehof, editor, 9th International Conference on Formal Structures for Computation and Deduction, FSCD 2024, July 10-13, 2024, Tallinn, Estonia, volume 299 of LIPIcs, pages 10:1–10:24. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2024.
[13] Krzysztof Kapulkin and Peter LeFanu Lumsdaine. The simplicial model of univalent foundations (after Voevodsky). J. Eur. Math. Soc., 23(6):2071–2126, 2021.
[14] János Kollár. Non-quasi-projective moduli spaces. Annals of Mathematics, 164(3):1077–1096, November 2006.
[15] Mihály Makkai. First order logic with dependent sorts, with applications to category theory. Preprint, Available on the web, Nov 1995.
[16] Mihály Makkai. Az absztrakt halmazok elmélete függő típusos elsőrendű logikára alapozva. Magyar Filozófiai Szemle, 58:69–92, 2014.
[17] Per Martin-Löf. An intuitionistic theory of types: predicative part. In H.E. Rose and J.C. Shepherdson, editors, Logic Colloquium '73, Proceedings of the Logic Colloquium, volume 80 of Studies in Logic and the Foundations of Mathematics, pages 73–118. North-Holland, 1975.
[18] The mathlib Community. The Lean Mathematical Library. In Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2020, page 367–381, New York, NY, USA, 2020. Association for Computing Machinery.
[19] John C. Reynolds. Types, abstraction and parametric polymorphism. In R. E. A. Mason, editor, Information Processing 83, Proceedings of the IFIP 9th World Computer Congress, Paris, France, September 19-23, 1983, pages 513–523. North-Holland/IFIP, 1983.
[20] Peter Scholze. Half a year of the Liquid Tensor Experiment: Amazing developments. blog post on the Xena project's website. https://xenaproject.wordpress.com/2021/06/05/half-a-year-of-the-liquid-tensor-experiment-amazing-developments/, 2021.
[21] Georg Schumacher and Hajime Tsuji. Retraction: “Quasi-projectivity of moduli spaces of polarized varieties”. Annals of Mathematics, 198(3):1305, 2023.
[22] The Univalent Foundations Program. Homotopy Type Theory: Univalent Foundations of Mathematics. https://homotopytypetheory.org/book, Institute for Advanced Study, 2013.
[23] Vladimir Voevodsky. Univalent foundations. Slides for a talk at the Institute of Advanced Study, Princeton, March 2014.











