„Az okos ember mások hibájából tanul” – tartja a népi bölcsesség. A matematikában – ahol a precizitásnak és a minden részletre való odafigyelésnek olyan jelentős a szerepe – mégsem elterjedt a hibák gyűjtése, bemutatása, elemzése. Vannak híres, nevezetes hibák, és természetesen minden általános iskolai, középiskolai vagy éppen egyetemi tanár tisztában van az aktuálisan tanított témakör buktatóival, és erre általában fel is hívja a tanulói figyelmét, sőt a hibás megoldások elemzésének – matematika-módszertannal foglalkozó – kutatói hibatípusokat azonosítanak, elemzési modelleket állítanak fel, és mérik a rendszeres hibaelemzés jótékony hatását a problémamegoldásra, mégis ritkán találkozni feladatgyűjteményekben „Miért hibás az alábbi gondolatmenet?” vagy „Melyiküknek van igaza?” típusú elemző feladatokkal.
Ezért nagyon megörültem, amikor Ujházy Márton barátom figyelmembe ajánlotta a budapesti Fazekas Mihály Gimnázium Orosz Gyula által tartott „Hibás megoldások” című minikurzusát, amely sok hiba és módszertani érdekesség megismerésével kecsegtetett. A jó hangulatú délután számomra legváratlanabb fejleménye az volt, amikor az előadó megtekintésre bocsátotta a témában megjelent könyveit. A többes szám helyes: két – nem éppen vékonyka – műve is olvasható már. A következőkben a szerző és könyveinek rövid bemutatása olvasható. Itt fejezem ki köszönetemet a MATEGYE Alapítványnak, hogy a könyvajánlóhoz rendelkezésemre bocsátotta a műveket!
Orosz Gyula a budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium elismert matematikatanára, aki sok évtizedes tapasztalattal vezeti a középiskolás diákok tehetséggondozó szakköreit. Számos cikk, tanítási anyag szerzője, továbbá minikurzusok és versenyfelkészítők szervezője, ahol diákoknak, illetve tanároknak szemléletesen mutatja be a problémamegoldás és a kreatív gondolkodás módszereit. Pályafutása során több szakmai elismerésben is részesült: 2014-ben a Fazekas Gimnázium vezetőtanáraként Beke Manó emlékdíjat kapott, 2021-ben pedig kiemelkedő tehetséggondozó munkájáért az „ERICSSON a matematika és fizika tehetségeinek gondozásáért” díjat is elnyerte. Az általa vezetett szakkörök és kurzusok évente több tucat diákot készítenek fel versenyekre és érettségire, akiknek sikerei jól mutatják pedagógiai módszereinek eredményességét.

A kecskeméti MATEGYE Alapítványnál 2020-ban megjelent, Hibás feladatmegoldások az általános iskolában című könyvének folytatásaként idén tavasszal a Hibás feladatmegoldások a középiskolában című munkája is napvilágot látott. Mindkettő rendhagyó módon közelíti meg a matematikai gyakorlást: nemcsak az „egyik helyes” útvonalat, azaz a megoldást mutatják be, hanem a tanulók és tanárok számára egyaránt rendkívül értékes hibaanalízist kínálnak. A művek előszavában a szerző írja: a hibák „módszertani szerepe nagyon fontos, egyfajta hatékonyságnövelő funkciójuk van”, hiszen „az elkövetett tévedés emlékezetes marad, a saját hibájára mindenki hosszabban emlékszik, s így nehezebben követi el újra azt”. Fontos hozzátenni, hogy természetesen ehhez szükség van a reflexióra, a (például dolgozatban elkövetett) hiba alapos és mély elemzésére. A kötetek nyilván nem reprezentálhatnak minden, diákok által elkövethető hibát, de a felsorakoztatott feladatok széles spektruma, amely az órai gyakorlópéldáktól kezdve az érettségi feladatokon át a verseny szintű problémákig tart, mindenki számára tartogat kihívásokat, így minden matematikatanár haszonnal forgathatja.

A két mű anyaga nagyon bőséges: a 26-26 téma összesen 380 oldalt tesz ki; a kiválasztott témák pedig tematikusan rendszerezik az általános iskolai, valamint a középiskolai tananyag területeit: az algebrai átalakításoktól kezdve a halmazelméleten és kombinatorikán át a trigonometriai egyenletekig, nem beszélve a nehezebb területekről (például inverz görbék, differenciál- és integrálszámítás) és a – hibatípusok szerinti – módszertani témakörökről (például hibás sejtések, szűkítő azonosságok, kerekítés, alulhatározott feladatok, nyelvi problémák). A jellemzóen szakköri feldolgozás során előkerülő témákat (például játékok, algoritmusok) is tárgyalja a szerző.
A könyvek három, egymásra épülő részre tagolódnak: az elsőben a feladatok gyűjteménye található, a másodikban a diákok gyakran elkövetett tévedéseit bemutató hibás megoldások, a harmadik pedig a megoldások részletes, módszertani elemzését tartalmazza.
A hibák jellege nagyon változatos. Egyes feladatokat látva rögtön sejtheti a gyakorló tanár, hogy mire kell majd figyelni a hibás megoldás olvasása közben, de gyakran könnyű első olvasásra átsiklani egy-egy hiányzó szón, téves feltételezésen, apró hibán, avagy elbukni: hosszas gondolkodás után a könyv végi elemzéshez lapozni és aztán a homlokunkra csapni – „hát persze, ez nyilvánvaló!”. Több időt igénylő, ugyanakkor nagyon hasznos hozzáállás, ha nem lapozunk rögtön a hibához, hanem megoldjuk a feladatot magunktól, majd keressük, hogy itt mit is gondolhattak tévesen a diákok. Néha éppen azt, amit mi. Ha nem, akkor viszont üdítően hathat ránk egy-egy érettségi feladat megoldókulcsának utólagos bővítését látva a diákok kreatív asszociációs készsége – „így is lehet értelmezni a feladatot?”.

Kedvcsináló példaként bemutatjuk az egyik feladat és hozzá tartozó hibás megoldás párt, valamint a megoldás elemzésének rövidített változatát.
11.7. feladat: Egy osztályban franciául 10-en, angolul 20-an, németül 25-en tanulnak. Franciául és angolul 5, angolul és németül 6, németül és franciául 8, végül mindhárom nyelven 2 diák tanul. Hányan tanulják a három nyelv valamelyikét?
Hibás megoldás: Jelölje 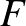 ,
, 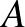 ,
,  rendre a francia, angol és német nyelven tanulók halmazát. A logikai szitaformulát alkalmazzuk, mely szerint
rendre a francia, angol és német nyelven tanulók halmazát. A logikai szitaformulát alkalmazzuk, mely szerint
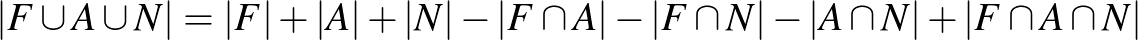 .
.
A formula alapján
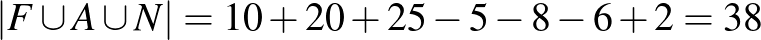 ;
;
vagyis 38-an tanulják a három nyelv valamelyikét.
Elemzés: a 3 halmaz viszonyát szemléltető Venn-diagram megfelelő osztályainak elemszámait jelöljük meg ismeretlenekként, majd a feladat feltételei alapján írjunk fel egyenleteket. Az egyenletrendszer megoldása után a csak franciát tanulók számára 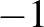 -et kapunk, ami nyilván ellentmondás. Itt tehát az a hiba, hogy a szita formula alkalmazásakor feltettük, hogy van megoldás. Hiányzott a konstrukció, hogy ti. a megfelelő részhalmazra bontás ténylegesen előállítható.
-et kapunk, ami nyilván ellentmondás. Itt tehát az a hiba, hogy a szita formula alkalmazásakor feltettük, hogy van megoldás. Hiányzott a konstrukció, hogy ti. a megfelelő részhalmazra bontás ténylegesen előállítható.
A 2. kötet tartalomjegyzéke:
| # | Fejezet címe | Feladatok | Hibás megoldások | Elemzés |
| 1 | Szűkítő, bővítő azonosságok | 7 | 47 | 121 |
| 2 | Másodfokú kifejezések | 7 | 49 | 123 |
| 3 | Algebra | 8 | 50 | 124 |
| 4 | Egyenlet, egyenletrendszer, egyenlőtlenség | 10 | 51 | 126 |
| 5 | Számelmélet | 12 | 53 | 130 |
| 6 | Koordináta-geometria | 13 | 57 | 133 |
| 7 | Háromszögek | 13 | 61 | 136 |
| 8 | Sokszögek | 15 | 67 | 145 |
| 9 | Körök | 16 | 70 | 149 |
| 10 | Térgeometria | 17 | 75 | 153 |
| 11 | Gondolkodási módszerek | 18 | 77 | 158 |
| 12 | Kombinatorikus geometria | 20 | 82 | 161 |
| 13 | Játékok | 21 | 85 | 174 |
| 14 | Sorozatok | 22 | 88 | 179 |
| 15 | Függvények, szélsőérték | 24 | 91 | 183 |
| 16 | Inverz görbék | 26 | 94 | 187 |
| 17 | Analízis | 27 | 97 | 190 |
| 18 | Differenciálszámítás, integrálszámítás, terület | 28 | 98 | 196 |
| 19 | Statisztikai paradoxonok | 31 | 100 | 202 |
| 20 | Valószínűségszámítás | 32 | 103 | 207 |
| 21 | Kerekítés | 33 | 105 | 209 |
| 22 | Állítások megfordítása | 35 | 108 | 214 |
| 23 | Alulhatározott feladatok | 36 | 110 | 218 |
| 24 | Túlhatározott feladatok | 38 | 113 | 222 |
| 25 | Nyelvi problémák | 39 | 115 | 225 |
| 26 | Vegyes feladatok | 40 | 117 | 227 |
Tehát ez a két könyv nem egyszerű feladatgyűjtemény, hanem a matematikai gondolkodás csapdáit tárja elénk, és vezet végig a helyes úton. Középiskolai diákoknak, érettségire készülőknek, versenyfelkészítőknek, valamint minden olyan pedagógusnak ajánlom, aki hisz abban, hogy a hiba nem baj, hanem lehetőség a gondolkodásra: a tévedésekből tanulva válik igazán biztos és használható tudássá a matematika.
ELTE TTK Matematika Intézet
Matematikatanítási és Módszertani Központ











