A tanterem már nem elég!

Tehetséggondozás és felzárkóztatás a BME Alfa online felületen

A gazdasági, műszaki és természettudományos karok oktatói és hallgatói évek óta azzal szembesülnek, hogy a felsőfokú tanulmányok megkezdésekor a hallgatók nagy része az elvárt szintnél jóval gyengébben teljesít. Ez vonatkozik a matematikára és a fizikára is. Nekünk, egyetemi oktatóknak ez komoly fejfájást okoz. Nem nézhetjük tétlenül, hogy a fiatalok júniusban sikerélményekkel telve elvégzik a középiskolát, magas pontszámmal felvételt nyernek az áhított felsőoktatási intézménybe, majd szeptember közepén már sokaknak a teljes sikertelenséggel és önnön alkalmatlanságuk érzésével kell birkózniuk. A jelenség hátteréről, a gondok enyhítését célzó intézkedésekről, törekvésekről számos beszámoló született: Csákány (2013), Radnóti–Nagy (2014).

Felzárkóztatás

A tanulásszervezés, a tudásszerzés és a tudás alkalmazása a technológiafejlődésnek és a társadalmi változásoknak köszönhetően megváltozott. A digitalizáció, az okos eszközök elterjedése, a hallgatók tudásszintjében és motivációjában meglévő hatalmas különbségek ösztönöztek minket arra, hogy keressünk olyan eszközt, amely nagyfokú önállóságot és egyénre szabott gyakorlási lehetőséget biztosít. Így jött létre 2012-ben a BME Alfa interaktív gyakorlófelület. Az ingyenesen elérhető BME Alfa olyan weblap, amely elsősorban a középiskolások és a kezdő egyetemisták önálló tanulását hivatott segíteni. Alapja a Moodle e-Learning keretrendszer, amelyet testre szabtunk a lokális igényeket figyelembe véve. Egy standard Moodle (vagy egyéb ún. Learning Management System, röviden LMS) installációval szemben az a lényeges különbség, hogy a BME Alfa mindenki számára nyitott, tehát a felhasználók jelentős része nem az intézmény hallgatója. Ennél fogva a hangsúly nem azon van, hogy egy-egy kurzus teljesítését nyomon tudja követni az oktató, hanem azon, hogy a felhasználó minél több feladathoz hozzáférjen, az ország bármely településéről vagy külföldről egyaránt.

A rossz kezdés okozta csalódottságon sokan nem tudnak egyedül túljutni. Számukra lényegében már a félév elején kódolva van a sikertelen vizsga matematikából vagy fizikából. Annak érdekében, hogy az elsőéves hallgatók minél hamarabb szembesüljenek azzal, mi az a szükséges matematika- és fizikatudás, ami kell ahhoz, hogy sikeresen teljesítsék az első félévben felvett tárgyakat, a Műegyetem 2010-ben bevezette az ún. nulladik zárthelyit, amit az első oktatási héten írnak meg a gólyák (Csákány–Pipek (2010)). Matematikából ez egy 15 kérdésből álló teszt, amely teljes egészében lefedi a középszintű középiskolai tananyagnak azon részét, aminek ismerete az egyetemi tanulmányok megkezdéséhez elengedhetetlen. A nulladik zárthelyin minden kérdéshez öt válaszlehetőség tartozik, minden helyes válasz 4 pontot, a rossz válaszok −1 pontot érnek. A nulladik zárthelyi sikeres teljesítéséhez az összesen megszerezhető 60 pontból 24-et kell elérni, a munkára a hallgatóknak 50 perc áll rendelkezésükre, és semmilyen segédeszköz nem használható. Az eredményességről, tapasztalatokról már korábban születtek cikkek, konferencia-előadások (Csákány (2013)). A félév legelején megírt felmérő és annak az eredménye nagyon hasznos a hallgató számára, de nem elég. Segíteni kell és biztosítani kell a felkészülés lehetőségét is.

Mára a felzárkóztatás, a felsőoktatásba történő zökkenőmentes átlépés elősegítése szinte minden felsőoktatási intézményben elengedhetetlen feladat. A nulladik zárthelyi sikeres teljesítését elősegítendő a BME Matematika Intézet Kecsap néven nyár végi önköltséges felzárkóztató tanfolyamot indít az érdeklődő hallgatóknak, általában 250–300 gólya részvételével. Azok számára, akik a nulladik zárthelyin nagyon gyengén teljesítettek, Bevezető matematika és Bevezető fizika címmel speciális kurzusokat vezettünk be. Az Alfa gyakorlófelületnek ezeken a kurzusokon is nagy szerep jut. A példatárban meglévő nagyszámú feladat és teszt alkalmas arra, hogy az oktató házi feladatokat adjon, illetve a hallgatók a saját igényük szerint gyakoroljanak, tematikus feleletválasztós teszteket oldjanak meg. A hallgatók azonnal kapnak visszajelzést az elért eredményükről, megnézhetik a részletes megoldásokat. Az oktatók folyamatosan nyomon követhetik az Alfa honlapon a házi feladatokkal kapcsolatos hallgatói aktivitást. Látható, hogy melyik hallgató mely feladatokkal foglalkozott, mennyi időt töltött a feladatok megoldásával, és természetesen az is, hogy a feladatban szereplő kérdésre helyes választ adott-e. Ezek fontos információk az oktatónak, mert ez alapján látja, hogy hol tartanak a hallgatók a tananyag elsajátításában, megértésében, és eldöntheti, hogy egy adott anyagrésszel szükséges-e még többet foglalkozni.

Egyes források szerint több tízezer informatikus hiányzik az iparból ma Magyarországon. A hiány enyhítése érdekében 2018-ban a Műegyetemen elindult az ún. BProf (Bachelor Profession) képzés, informatikus üzemmérnök képzés. A képzés gyakorlatorientált: a cégeknél, vállalatoknál végzett munkán és tapasztalatszerzésen van a hangsúly. Az alapozó tárgyak szűkre szabott kontaktóra-keretét is hatékonyan, személyre szabottan tudjuk kompenzálni a BME Alfa gyakorlófelület bevonásával.

Tehetséggondozás, pályaorientáció

A matematika, a természettudományos és műszaki (Science, Technology, Engineering and Mathematics, röviden STEM) tárgyak tanítása a fejlett országokban is súlyos gondokkal küzd. Tapasztaljuk, hogy a kormányzati intézkedések ellenére, folyamatosan csökken a diákok érdeklődése a természettudományos és műszaki pályák iránt. Ennek leküzdésére a felsőoktatási intézményekben a tehetséggondozás, a felzárkóztatás mellett nagyon komoly erőfeszítéseket tesznek annak érdekében, hogy népszerűsítsék ezeket a pályákat a középiskolások körében. A természettudományok iránti pozitív hozzáállás kialakítása, a természettudományos pályák iránti érdeklődés növelése már általános és középiskolásokra is kiterjed (BME Gyerekegyetem, BME Science Camp).

A Műegyetemi Alfa Matematika pontgyűjtő verseny szintén a középiskolásoknak (9–12.-esek) szól. 2015-ben, amikor először meghirdettük a versenyt, tudtuk, hogy rengeteg versenyzési lehetőség érhető el a diákok számára. A létrehívásakor az volt a célunk, hogy minél több diákkal, pedagógus kollégával alakítsunk ki tartós, folyamatos kapcsolatot. Minél több középiskolásnál érjük el azt, hogy külső kényszer nélkül, stresszmentesen, rendszeresen foglalkozzon matematikával. Olyan diákoknak is nyújtson versenyélményt (a kudarcélmény lehetőségének kizárásával), akiket a környezet nem ösztönöz eléggé, akik nem merik vállalni a nyilvános megmérettetést, vagy akiknek a földrajzi távolság, a verseny helyszínére való eljutás is gondot okozhat. A verseny maga, 6 online fordulóból, előre megadott tematikával és az online fordulókon elért eredmények alapján meghívott diákoknak szervezett döntőből áll. Az online fordulók természetesen anonimek és nem derül ki, hogy mely intézményekből valók a diákok. A döntőben való részvételhez viszont személyes megjelenés szükséges. A döntőt, az online fordulókkal megegyező körülmények között, de a BME Matematika Intézet számítógéptermeiben tartjuk. A versenyben két korcsoportot különböztetünk meg: 9−10. osztályosok és 11−12. osztályosok. A nagyobbak két különböző nehézségi szint közül is választhatnak. Az egyik szint nem mutat túl a középszintű érettségi színvonalán, a másik az emelt szintű érettségit célozza meg. Ezzel a bontással azt szerettük volna elérni, hogy bárki sikeres lehessen, és bárki hozzájusson a sikeres feladatmegoldás öröméhez. A nehézséget nem a példák összetettsége, bonyolultsága jelenti, hanem az, hogy meghatározott számítógépidő felhasználásával kell megoldani az aktuális feladatsort. Egy-egy feladatsor megoldására két hét áll rendelkezésre. A beküldési határidő letelte után a részletes megoldások azonnal felkerülnek a honlapra, hogy ezzel is segítsük az otthoni tanulást, gyakorlást. A gyakorlófelületen meghirdetett verseny másik nagy előnye, hogy a határon túlról is bárki bekapcsolódhat. Ezeknek a diákoknak az arányát – mivel az online fordulók anonimek – nem tudjuk pontosan megmondani, de azt látjuk, hogy a döntő 25–30 versenyzője (tehát a legjobbak) között mindig akad 3–5, aki az országhatáron túlról érkezik, még akkor is, ha maga az utazás is okozhat nehézséget.

Sajnos 2020-ban a koronavírus-járvány miatt a legjobbak számára szervezett döntőt is online formában kellett megtartani. Erre a 25 legjobb eredményt elérő diák kapott meghívást − nagyon sok vidéki és néhány határon túli településről.

Érdekes lehet megnézni, az évek során hogyan alakult a versenyzők átlagos teljesítménye, kategóriákként, az egyes témakörökben.

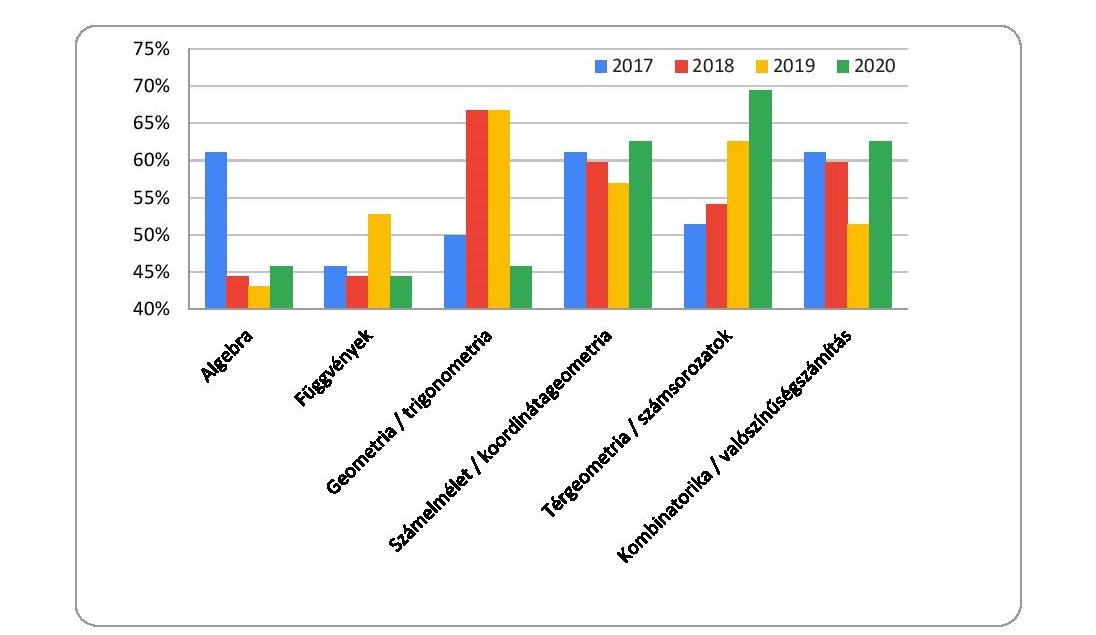
Demokratizálódás és esélykiegyenlítődés a tanulási folyamatban

Mind a felkészítő kurzusok, mind az új üzemmérnökképzés tanulságokkal szolgál arra nézve, hogy a közép- és felsőoktatás társadalmi háttere és funkciója hogyan változott az utóbbi évtizedekben, és ezek miféle új kihívások elé állítják az oktatásszervezőket. Az általános tankötelezettség társadalmi funkciója ma már nem az, mint 60 évvel ezelőtt volt, amikor a társadalmi mobilitást segítette elő. Nem a magasabb társadalmi státusba kerülés készteti a diákságot a középiskolai évek során a tudomány elsajátítására, a tantárgyak iránti érdeklődés erősen alábbhagyott az utóbbi évtizedekben. Az egyetemre kerülés esetében még megvan az a hajtóerő, hogy a hallgatók felsőbb szaktudás megszerzése révén szeretnének magasabb státusba kerülni, de akkorra a motiváció már kevés, a korábban elmulasztott alapozás komoly nehézséget okoz a továbbhaladásban. A középiskola időszakában a tudomány iránti érdeklődést már nem lehet pusztán az unásig ismételt „ha nem tanulsz, kukás lesz belőled” vagy az „ez van, ezt kell szeretni” szólamokkal kiváltani. Elengedhetetlen, hogy a felsőoktatási intézmények már a felsőbb tanulmányok megkezdése előtt is részt vegyenek a diákok motiválásában. Ennek módja az olyan programok indítása, amibe középiskolások is teljesen akadálytalanul bekapcsolódhatnak. Kétségkívül ilyen kezdeményezés akár a BME Alfa gyakorlófelület, akár a minden évben megszervezett ingyenes BME online matematikaverseny és közös felkészülés az érettségire. A pontversenyben nem csak olyanokat céloztunk meg, akik egyébként is a nagy hagyományokkal rendelkező magyar tanulmányi versenyekre rendszeresen jelentkeznek, hanem azokat is, akik még sosem voltak versenyen, de kipróbálnák magukat egy rendszeres, a középszintű érettségi nehézségének megfelelő feladatmegoldó kurzusban. Nyilván a versenyszerűen matekozó gyerekeknek ez nem kihívás, de azoknak, akik rendszeres külső motiválást igényelnek, azoknak egy kellemes matematika közeli élményben lesz részük.

A diákok önálló tanulásszervezése ma már nem kívülről kikényszerítendő cél, hanem – ha kellő nyitottsággal tekintünk a jelenségre – napi tapasztalat, feltéve, hogy a tudásnak nem a klasszikus forrásait – a tankönyveket és a tanárt – látjuk csak a szemünk előtt. Az 1960-as évek társadalmi-kulturális változásai után a tekintélyelvű oktatási-nevelési kultúra szépen lassan demokratikusabb irányba tolódott el, az intézmények részéről lassabban, a diákság autonóm tevékenysége folytán gyorsabban. Ma már nem a tanár és a tankönyv a tudás kizárólagos forrása. Még kevésbé feladata és lehetősége a tanárnak a fegyelemre és engedelmességre nevelés. Az ennek való megfelelést a diákoktól ma elvárni hiú ábránd, ráadásul távol áll azoktól a céloktól, amit ma a tudomány a pedagógia céljaként értelmez. A tanulás terei már nem korlátozódnak az osztálytermekre, nem azért, mert a közoktatásnak ez ne lenne törekvése, hanem mert a diákok egyszerűen más helyre fókuszálják a figyelmüket. A tudás megszerzésére irányuló figyelem a diákság részéről ma már az online terekre helyeződik át. A diák a saját tanulását ma már önállóan szervezi, vagy nem szervezi, mindenesetre a tanárnak ebben csak a segítő szerepe jut.

A globalizáció és az online terek jelentőségének felerősödése a kisebbségeket és a társadalmi szempontból hátrányosabb helyzetben lévőket is segítheti a korábbi, lokális gyökerű, társadalmi korlátok leküzdésében. Például a határon túli magyaroknak már nem kell Budapestre utazniuk, hogy részesülhessenek a magyarországi természettudományos kultúrából. A gyakorlófelület és az online verseny számukra is elérhető, és élnek is a felajánlott lehetőséggel.

Rendkívül figyelemreméltó fejlemény, hogy a végzős korosztály esetén az országban szinte egyedüliként a BME Alfa matematikaversenyen valósul meg évről évre a lány és fiú résztvevők kiegyensúlyozottsága. A jelentkezés online történik, a feladatok kiértékelését pedig gép végzi, és az Alfa versenyen szinte minden évben ugyanannyi lány kerül be a döntőbe és átlagosan ugyanannyi dobogós lesz, mint fiú. Közkeletű az a nézet, hogy a lányok egyáltalán nem rosszabbak a természettudományokból, mint a fiúk, csak a mérések még nem eléggé megfelelőek arra a célra, hogy ezt a kiegyensúlyozottságot kimutassák. Nos, a BME Alfa online verseny ezt az eredményt majdnem minden évben automatikusan hozza.

Tudástár, feladatbank

A verseny régebbi feladatai a megoldásokkal együtt megtalálhatók a https://alfa.bme.hu/ oldalon. Ez nem csak a tehetséggondozásban segíti a középiskolai tanárokat, de az átlagos képességű diákok oktatásában is nagy segítség lehet. Ismerünk eseteket, amikor a diákokkal együtt a tanár is belekukkant a versenypéldákba, hogy onnan ötletet nyerjen akár érettségire való felkészítéshez, akár a versenyfelkészítés céljából. A gondosan megválogatott feladatok olyanok, hogy azok a közép- és emelt szintű érettségi követelményeknek megfeleljenek. Emellett olyan példák is bekerültek a feladatok közé, amelyek ma már kimentek a divatból, de a 30–40 évvel ezelőtti felvételiken szívesen adták fel őket. Az Alfa, mint feladatbank, tehát nem csak a jelent tükrözi, hanem a matematikai kulturális örökséget is ápolja. Erre garancia, hogy a feladatokat mind gyakorló tanárok, mind (adott esetben éppen a megfelelő témát kutató) egyetemi oktatók készítik.

Az idei tavasz megmutatta, hogy ez a matematikaverseny nem csupán egy csepp a tengerben, hanem azok közé a kevesek közé tartozik, amelyet meg is lehetett tartani. A rekordszámú jelentkező is igazolja, hogy van létjogosultsága, haszna a versenyünknek.

Nemzetköziesítés

Mind matematikából, mind fizikából a feladatok egy része angol nyelven is elérhető. Jó döntés volt ebbe az irányba is lépéseket tenni, mert így alkalmassá vált a rendszer a Műegyetem iránti külföldi érdeklődők (akik például a Stipendium Hungaricum program keretében jöhetnek Magyarországra) felvételi vizsgára való felkészülésére és a vizsga megszervezésére is.

Az Alfa gyakorlófelület használatának területi eloszlása:

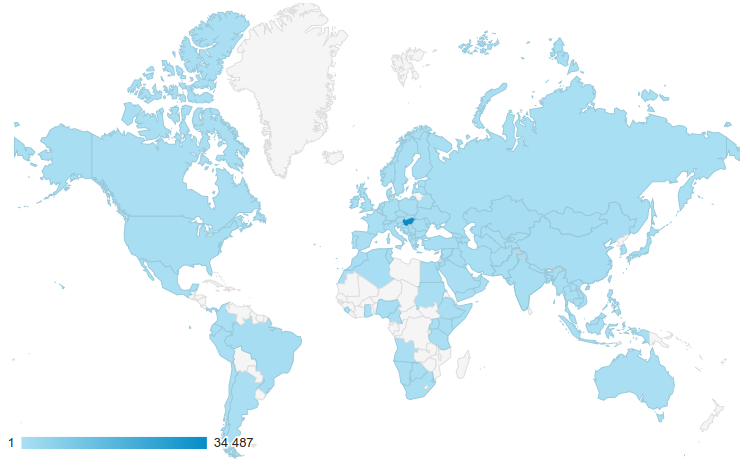
Hivatkozások

Baranyi Máté, Molontay Roland (2019): Effect of Mathematics Remediation on Academic Achievement – A Regression Discontinuity Approach In: 2019 International Symposium on Educational Technology (ISET) Hradec Králové, Csehország : IEEE, (2019) pp. 29–33.

Csákány Anikó (2013): Mit tudnak az elsőéves műegyetemi hallgatók a vektorokról? Acta Carolus Robertus, 3 (1), pp. 189–196. http://epa.niif.hu/02400/02498/00005/pdf/EPA02498_acta_carolus_robertus_2013_1_189-196.pdf

Csákány Anikó és Pipek János (2010): A 2009 szeptemberében a műszaki és természettudományos szakokon tanulmányaikat kezdő hallgatók által írt matematika felmérő eredményeiről. Matematikai Lapok, 16 (1), pp. 1–15.

Radnóti Katalin és Nagy Mária (2014): A matematika szerepe a természettudományos képzésben. Új Pedagógiai Szemle, 64 (5–6), pp. 89–102. http://folyoiratok.ofi.hu/uj-pedagogiai-szemle/a-matematika-szerepe-a-termeszettudomanyos-kepzesben

Molnár Zoltán (2018): Milyen matematikát kell tanítanunk és azt hogyan? Új Pedagógiai Szemle, 2018. 5-6., pp. 86-108.

A szerzők az Alfa csapatának tagjai: Gergi Miklós¹,Kiss Sándor¹, Lángné Dr. Lázi Márta¹, Molnár Zoltán¹, Nagy Ilona¹,Pécsi István², Péterné Kovács Anikó¹, Rácz Éva³, Ruppert László³.