Műszaki és természettudományok közelről
BME TTK Science Camp
„A ma tudománya a jövő technológiája”

A Budapesti Műszaki és Gazdaságtudományi Egyetem Természettudományi Kara Science Camp néven 2016. óta szervez ingyenes természettudományos tábort középiskolás diákoknak. Felismertük ugyanis azt, hogy a természettudományos képzésben részt vett hallgatóink (fizikusok, matematikusok) igen sikeresek a műszaki és pénzügyi cégek (bankok, biztosító társaságok) munkatársaiként amellett, hogy igen sokan tudományos pályán is aktívak. Hisszük, hogy a műszaki és pénzügyi területen aktív cégek joggal tartanak igényt olyan szakember-utánpótlásra, akik nem specializálódtak egy-egy műszaki területre, hanem a természettudományos képzésükből adódóan széles látókörrel, komplex problémamegoldó képességgel és nagyfokú flexibilitással rendelkeznek.
A fejlett országokban is megfigyelhető az az aggasztó jelenség, hogy csökken a diákok érdeklődése a természettudományok, a technológia, a műszaki tudományok (a Science, Technology, Engineering, and Mathematics angol kifejezés kezdőbetűiből alkotott rövidítéssel: a STEM tárgyak) iránt, miközben a tudásalapú gazdaságban egyre nagyobb szükség van a STEM készségekkel rendelkező szakemberekre. A felsőoktatás számára jelenleg nem az jelenti az igazi kihívást, hogy a sok jó diákból hogyan válassza ki a legjobbakat, hanem az, hogy találjon elegendő diákot, akit érdemes beiskolázni. A STEM tanulmányok iránti alacsony érdeklődés okai többek között, hogy a diákoknak sokszor nincs reális képe a STEM szakmákról és karrierlehetőségekről, és mivel e terület gyorsan változik, gyakran a tanáraiknak vagy a pályaorientációs tanácsadóknak sincsenek friss információi, amivel segíthetnék a diákok döntését.
A modern kor ellentmondásához tartozik az is, hogy egy sikeres karrierhez elvben egyre nagyobb ismeretmennyiség birtoklása szükséges. A fiatalok figyelmét mégis igen nehéz az ismeretek átadása során fenntartani. Általános az a vélekedés: minek annyit tanulni, minden tudás az interneten hozzáférhető, ami pár gombnyomással állandóan elérhető a telefonunkon! Konkrét példát véve, ha valakit a nukleáris energetika vagy a pénzügyi matematika érdekel, akkor néhány Wikipedia szócikket 10 perc alatt elolvasva az átlagismeretek szintjénél magasabb tudást szedhet fel. Azonban ez a ,,tudás" gyorsan el is múlik, és nem fog összekapcsolódni más ismeretekkel, nem válik tehát gyakorlatban is alkalmazható mély ismeretté.
A fent említettek következtében felértékelődik az első kézből való ismeretszerzés, és az élményalapú tanulás fontossága. Közvetlenül látni azt, hogy Magyarország energiatermelésének felét hogyan lehet néhány üzemcsarnokban előállítani (Paksi Atomerőmű), vagy látni egy nemzetközi szinten is sikeres félvezetőipari cég (Semilab Zrt) űrtechnológiát idéző gyártósorát: mindez alázatra, szorgalomra és érdeklődésre serkentheti a fiatalokat. Az Országos Onkológiai Intézet, vagy a BME Ipar 4.0 kiállításának megtekintése során a diákok meggyőződhetnek arról is, hogy a kutatások eredményei milyen rövid idő után, milyen széles körben hasznosulnak és válnak a társadalmat közvetlenül befolyásoló tényezővé.
A rendezvényről
A tábort hazai és határon túli középiskolások számára egyhetes, ingyenes, bentlakásos, teljes ellátást biztosító formában hirdettük meg. A jelentkezéshez az egyéni motivációs levélen túl tanári ajánlólevél is szükséges volt. A programok megvalósításában, a szabadidő hasznos eltöltésében a Kar szenior hallgatói segítettek. Így a segítő egyetemi hallgatókon keresztül közelebb kerülhetnek a diákok az egyetemi élethez.
A tábor céljáról
A tábor célja a fizika és a matematika sokszínűségének, más tudományterületekhez való kapcsolódásának (például műszaki, informatika, közgazdaságtudomány, orvostudomány, kémia) bemutatása. A célok között szerepel az egyetemi működés, a hallgatói élet megismertetése, közelebb hozása a programok megvalósításában résztvevő egyetemi hallgatókon keresztül. Felhívjuk a figyelmet a csapatmunka fontosságára is, ugyanis a legtöbb mérnöki, gazdasági, tudományos területen a sikeres eredmények csapatmunkában születnek.
Általános jelenség, hogy a természettudományok, a technológia, a műszaki tudományok és a matematika iránti érdeklődés csökken a fiatalok körében. Magyarországon egyre növekvő problémát jelent a tehetséges középiskolások elvándorlása, a természettudományos és a műszaki érdeklődésű középiskolások tehetséggondozása, pályán tartása.
A tábort és az azt követő programokat, akkor tekintjük sikeresnek, ha diákjaink közül minél többen folytatják felsőfokú tanulmányaikat hazai képzőhelyeken és ezen belül is a BME nyolc karának valamelyikén.
Sok esetben az ország távolabbi pontjain, vagy a határon túl élő fiatalok tartanak a nagyvárosi környezettől, és nem merik a fővárosi intézményeket választani. A Kar ezeknek a hátrányoknak a leküzdése érdekében kezdett a Science Camp nyári természettudományos tábor szervezésébe.
Adatok a három, korábban megvalósított táborról
Eddig minden évben többszörös volt a túljelentkezés. A négy tábor során összesen 226 diákot tudtunk fogadni. Közülük 111 volt a fiú és 115 a lány. A diákok Magyarországról és a határon túlról (Románia, Szerbia, Ukrajna, Szlovákia) érkeztek. Minden évben volt néhány olyan magyar diák, aki külföldön (USA, Németország, Belgium, Spanyolország) tanul (vagy él), és részt vett a táborban.
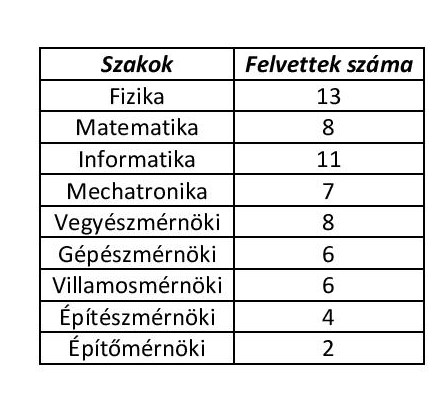
Azok közül, akik közben elvégezték a középiskolát, és jelentkezhettek a felsőoktatásba (az első 3 táborból, összesen 130 fő) 65 diák nyert felvételt a BME valamelyik szakára, az alábbi táblázat szerinti eloszlásban. (A 2020-as felvételi adatok még nem ismertek.)
A célközönség
A tábor célközönsége a pályaválasztás előtt álló, elsősorban a 10. és a 11. osztályt elvégzett középiskolás diákok. A tábori jelentkezők kiválasztásánál külön figyelünk arra, hogy esélyt kapjanak a hátrányosabb helyzetű térségekben élő és a határon túli magyar fiatalok is nagy számban. Számukra sokkal nehezebb egy Budapesten szervezett rendezvényre eljutni, vagy akárcsak egy ilyen lehetőségről értesülni, mint annak, aki a főváros vonzáskörzetében él. Mivel a tábort céges és társadalmi szponzorok adományai fedezik, így ezek az adományok közvetlenül ezeknek a fiataloknak a boldogulását is segítik.
A diákokat a széleskörű középiskolai reklámozást követően tanári ajánlás és egyéni motivációs levél után egy szakmai zsűri (tagjai a BME TTK vezető tanárai) bevonásával választottuk ki.
A sokféle, több helyszínen zajló, sűrű program megvalósításában az első perctől kezdve fontos szerepet szántunk az egyetemi hallgatóknak. (Főleg matematikus, fizikus, kognitívtudományi, vegyészmérnök stb. szakos hallgatók) Aktívan közreműködnek a helyszínek közötti eligazodásban, a kollégiumi életbe való beilleszkedésben, a közösségi programok megvalósításában, a verseny lebonyolításában. Egy-egy táborban a 60 középiskolást 20-21 hallgató segít. Ez a hallgatói létszám a középiskolások számát tekintve elsőre túlzottnak tűnhet. Azonban már az előkészületek során kiderült, hogy a hallgatókat sem egyszerű segítőknek, hanem aktív táborozónak kell tekinteni. Vagyis a szakmai programok fontos szerepet játszanak az ő természettudományos nevelésükben is, világszemléletük formálásában, a választott szakuk iránti elkötelezettségben. Amellett, hogy jelentős szerepet vállaltak a tudás közvetítésében például a személyes beszélgetések kapcsán, a tábor alkalmat adott a társadalmi felelősségvállalásra.
A programokról
A tábor céljának megfelelően olyan témákat, kutatási területeket kívántunk felvillantani, amelyekkel a középiskolai tanulmányaik során nem találkozhatnak a diákok, és amelyek várhatóan a pályafutásuk során meghatározóak lesznek.
A tábor tematikájában olyan programok szerepeltek, amelyek megerősítik a természettudományos alapokat, ismereteket, akár a műszaki tudomány, akár a természettudományos képzések vagy a közgazdaságtudomány terén képzeli el valaki a továbbtanulást.
A hét során az érdeklődők tudományos előadásokat hallgattak, versenyfeladatokat oldottak meg a fizika, a nukleáris technika, a matematika, az orvosi fizika és a pénzügyi matematika stb. területéről. Önálló műhelymunkát végeztek. Külső helyszíneket látogattak meg, felhasználva a Műegyetem biztosította szellemi hátteret, és a végzett hallgatóink munkaerőpiacon szerzett sokrétű tapasztalatait. Egy másik szempont a csapatmunka fontossága volt, ugyanis a legtöbb mérnöki, gazdasági, tudományos területen a sikeres eredmények csapatmunkában születnek.
Mivel a diákok az ország nagyon távoli pontjairól, sőt a határon túlról is érkeztek, terveink között szerepelt a XI. kerület és a Műegyetem bemutatása mellett kulturális és sportprogramok szervezése.
Megtekinthető a hét részletes, megvalósított programja.
A nagyon gazdag program ellenére nem tudunk minden érdekes és fontos dolgot bemutatni. Annak érdekében, hogy folyamatosan fenntartsuk a Műegyetem közössége által művelt területek iránti érdeklődésüket, és egy kicsit kárpótoljuk azokat a diákokat, akik nem kerültek be a táborba, Science Campus címmel előadássorozatot szervezünk diákok, tanárok számára:http://felvi.physics.bme.hu/sciencecampus.
Visszajelzések
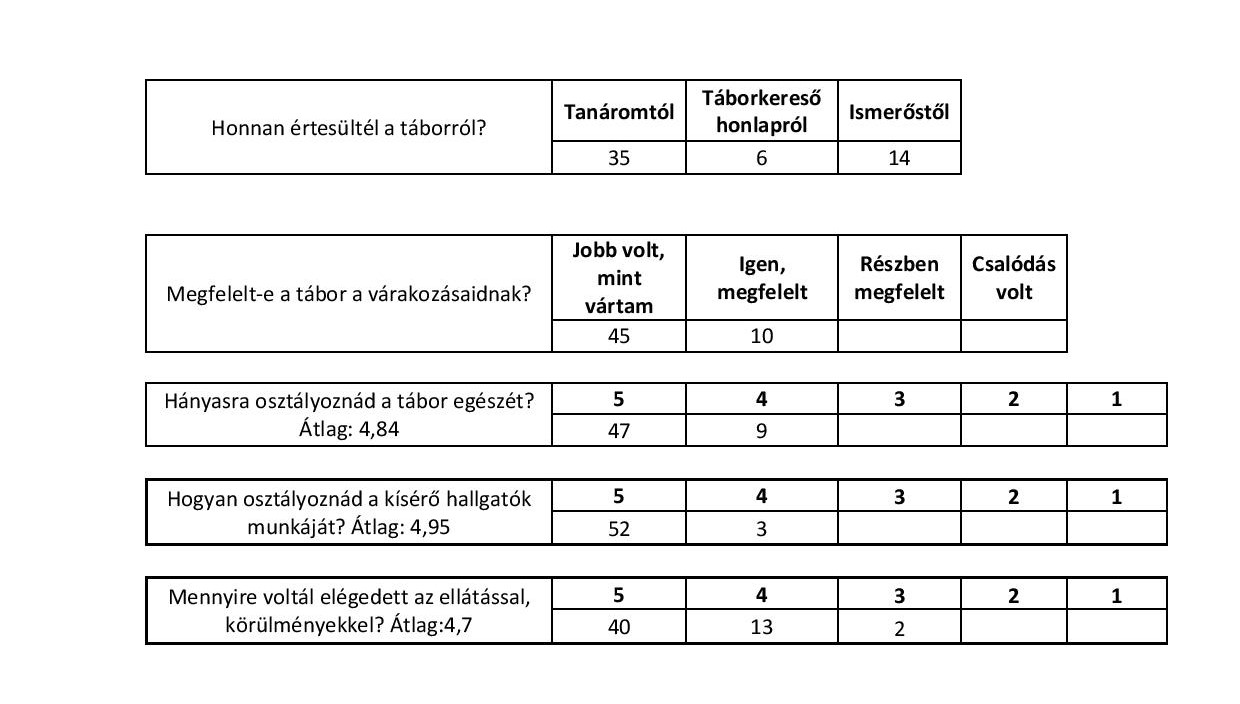
A tábor utolsó napján a diákok és a hallgatók is elégedettségi kérdőívet töltöttek ki. Ennek eredménye – a korábbiakhoz hasonlóan – nagyon jó. Sok hasznos észrevétel is érkezett, amelyeket a következő évi táboraink szervezése során figyelembe fogunk venni. Az osztályzatokból az olvasható ki, hogy nagyjából azonos a tábor megítélése, egyértelműen jó, nagyon jó. (Ez kívülről is érzékelhető volt, valahányszor találkoztunk a programokon, a kollégiumban kellemes, jó hangulatú, nyugodt – időnként nagyon is céltudatos csapattal – találkoztam.)
A megjegyzésekből, szöveges részekből viszont kitűnik, hogy nagyon különböző, változatos szociális helyzetű, hátterű, tág érdeklődési körrel rendelkező diákok jöttek össze. Szervezőként úgy gondolom, hogy ez a tapasztalat is hozzájárulhat a fiatalok társadalmi kérdések iránti érdeklődésének felkeltésében.
A különböző kérdésekre az alábbi válaszok érkeztek:
A táborban látottak, hallottak befolyásolják-e a pályaválasztásodat? Ha igen, akkor hogyan?
Többeket az egyetemválasztásban segítette, befolyásolta, vagy megerősítette a tábor, azaz egyértelműen, vagy bátrabban választanák a BME-t, annak valamelyik karát. Pl: 1. „Pozitív visszajelzést adott a BME-ről, amibe eddig nem láttam bele, így most sokkal árnyaltabb képet kaptam.” 2. „Elgondolkodtattak, mutattak más eddig számomra ismeretlen opciót.” 3. „Nem, de az egyetemválasztásom, BME mindenkit beelőz az országban.”
Többek esetében felkeltette a tábor az érdeklődést a TTK szakjai iránt, különösen a fizika iránt: 1. „Láttam, hogy a fizika jobb és kevésbé unalmas, mint gondoltam.” 2. „Beláttam, hogy a fizikus szak nem korlátozódik csak fizikára és nem igaz, hogy nem tudok majd elhelyezkedni, éppen ellenkezőleg. Kollégiumba is szívesen megyek.” 3. „Megtudtam, hogy fizikusoknak kutatáson kívül is van munkalehetőség, és ez segít, hogy a fizikusképzést válasszam.” 4. „Őszintén elgondolkodtam a fizika és egyáltalán a TTK karon, szakon, ugyanis eddig teljesen más irányokon gondolkodtam.” 5. „Igen, azt hiszem a tábor tulajdonképpen még jobban összezavart, még nem tudom, mi szeretnék lenni, kibővült a paletta, amiről választhatok.”
Az igennel válaszolók egy részénél nem lehetett beazonosítani, hogy pontosan mire is gondol. Pl. 1. „Igen, megerősített abban, hogy amit tervezek az milyen szép és érdekes szakma.” 2. „Igen, még jobban vonzanak a bemutatott szakok.” 3. „Igen, a fizika és a mérnöki tudományok során végzendő munkát rendkívül hatékonyan bemutatták számunkra, sőt mi magunk is részt vehettünk efféle programokban, kísérleteken. Jobban átlátom a hasonlóságokat, különbségeket, ami a hamarosan meghozandó pályaválasztási döntésemben segít.” 4. „Igen, őszinte véleményt hallhattunk az egyetemről, a karokról, az itteni életről.”
A szó szerint idézett válaszok azt is mutatják, hogy a diákokra mélyen hatott a tábor vagy szakmai, vagy emberi szempontból. Az a célkitűzés, hogy alternatívákat villantsunk fel a pályaválasztáshoz, megítélésünk szerint teljesült.
Támogatók:
Bepillantás a jövődbe! – Komplex műegyetemi pályaorientációs és továbbtanulást segítő programok (EFOP-3.4.4-16-2017-00025)

Együttműködő partnerek:

A tábor honlapja: http://sciencecamp.ttk.bme.hu/
További információk:
Szellemi éhség, érdeklődés és csapatmunka jellemezte az idei BME TTK Science Camp-et (Simon Ferenc, SEFI konferencia előadás, BME)
Videók: https://www.youtube.com/channel/UCURyeAht1XiQUNDrc9JtZ5w
„Gondolkozzunk előre. Ma holnapra, sőt sokkal továbbra.”






Lángné Lázi Márta
egyetemi docens
BME TTK Analízis Tanszék









