Információk

Főmenü

 Aktuális szám: 36. szám 2025. június 

36. szám 2025. június

Még több cikk

XIV. Leó pápa matematikából szerezte első diplomáját, a nemrég megválasztott román elnök pedig kétszer is maximális pontszámmal aranyérmes lett a Nemzetközi Matematikai Diákolimpián, és karrierje kutató matematikusként indult. Mi lehet még azokból, akik matematikus diplomát szereznek? Simon Péter és Molontay Roland ad néhány ötletet... (Fotó: Matematikus álláshirdetések a Profession.hu portálon.)

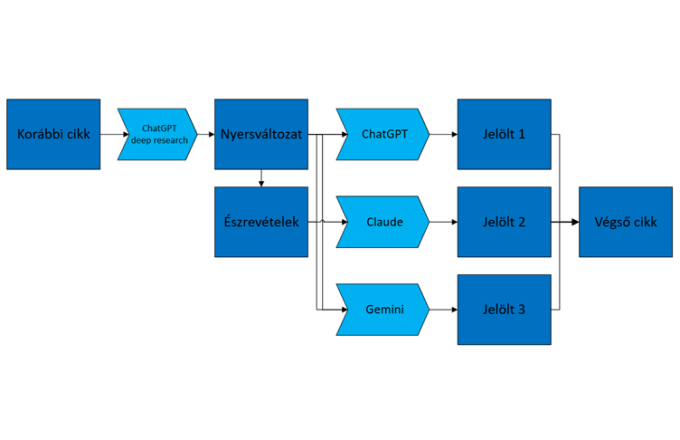
 Az Érintő előző számában Maga Balázs Simon Péterrel írt közös cikket a mesterséges neurális hálók gépi látásáról. Ezúttal egy másik, rendkívül izgalmas alkalmazási területet, azt, hogyan képes a mesterséges intelligencia szövegek megértésére és előállítására, vagyis a nagy nyelvi modellek létrejöttét mutatja be közösen Virág Fausztin Asztrikkal. A további szerzőtársakról az Utószóban olvashatnak...

2025. április 26-án egy országos matematikatanítási rendezvény zajlott le a HUN-REN Rényi Alfréd Matematikai Kutatóintézetben „Merre tart(son) a matematika tanítása Magyarországon?” címmel. A meghívottak között voltak matematikatanárok gimnáziumokból és szakképzési intézményekből, egyetemi oktatók és matematikusok az ország különböző pontjairól. A plenáris előadás újító javaslatairól és a munkacsoportokban megvitatott kérdések eredményeiről Csapodi Csaba számol be.

2025. március 27-én Kalmár László Emléknapot tartottak Szegeden a jeles matematikus, az informatika hazai úttörője születésének napra pontosan 120. évfordulóján. A Magyar Tudományos Akadémia Szegedi Akadémiai Bizottságának székházában elhangzott előadásokból Szabó Péter Gábor: Kalmár László, a matematikus című előadásának lejegyzett és szerkesztett változatát tesszük most közzé.

A Bolyai János Matematikai Társulat hagyományteremtő rendezvénysorozatához, a Matematika Világnapja (3.14) alkalmából megrendezett „Matek az utcán”-hoz 2025-ben minden eddiginél többen csatlakoztak. Országosan 20 helyszínen igyekeztek a matematika világát közelebb hozni az érdeklődőkhöz. (Fotónkon a Tatán készített piskóták.) Barbarics Márta néhány helyi szervező igencsak tanulságos π-napi beszámolóját szinte változatlan formában közölte...

Itt a 9. forduló! A Héttusa rovatban kitűzött feladatokra bárki beküldheti a megoldást. A feladat kérdésére a feladat sorszámát és a választ kell megküldeni a hettusa‍@‍ematlap.hu email címre. A beküldési határidő: 2025. július 14.  Az eddigi 8 forduló összesített eredménye, valamint az előző feladatsor megoldásai a megoldók ötleteivel kiegészítve szintén megtalálhatók a Héttusa rovatban. (A fotó forrása: dbhir.hu)

Idén ünnepli alapításának 200. évfordulóját a Magyar Tudományos Akadémia. Az MTA 199. közgyűlésének ünnepi ülésén, illetve a közgyűléshez kapcsolódó osztályrendezvényeken számos rangos tudományos díjat és elismerést adtak át. A díjazottak névsorában az Érintő szerkesztőbizottságának két tagja is szerepel: Oláh Vera és Röst Gergely. Gratulálunk nekik és a további díjazott matematikusoknak!

A Bolyai János Nemzetközi Matematikai díjat 2025-ben Kollár Jánosnak ítélte oda a Magyar Tudományos Akadémia Matematikai Tudományok Osztályának öt tagjából, valamint öt kiemelkedő külföldi matematikusból álló díjbizottság. Kéri Gerzson cikke főleg e díjról és díjazottjáról szól, de tisztázza, hogy mi  is a különbség Bolyai-díj és Bolyai-díj között. Idén ugyanis két különböző Bolyai-díjat is magyar matematikus kapott.

2025. május 13-án az MTA Dísztermében vehette át Stipsicz András a magyar tudományos élet kiemelkedő kutatójaként a Bolyai-díjat (Bolyai János alkotói díjat). A díjat odaítélő bizottság tagjai a tudományágak minél szélesebb körét képviselik, elnöke a mindenkori köztársasági elnök, további tizennégy tagjának felét a Magyar Tudományos Akadémia elnöke, másik felét pedig a Bolyai-díj Alapítvány alapítói delegálják. A Bolyai Jánosról elnevezett díjat matematikusként elnyerni különösen nagy jelentőségú.

Kollár János 2025-ben elnyerte a Bolyai János Nemzetközi Díjat, erről az Érintő két hírében is olvashatnak: Kéri Gerzson: A Bolyai-díjakról és a 2025-ös díjazottakról és Az MTA 199. közgyűlésének díjazottjai című cikkekben. Kovács Sándor írása Kollár János matematikai munkásságának egyik kiemelkedő részét, a magasabb dimenziós moduluselméletben elért eredményeit ismerteti meg az olvasóval.

A Rubik’s Gridlock (vagy Mondrian Blocks) egy régi eszme: „a játékok bevonása a tanulásba” megvalósítása egy új eszközzel, ami feleleveníti Dienes Zoltán és Varga Tamás XX. századi kísérleteit. Ez a modern, kézzelfogható, de később digitálisan is elérhető eszköz − egyelőre csak a kezdeti szakaszban, az óvodában és az alsó tagozaton − új lendületet adhat a matematika tanulásához. Vancsó Ödön, Kerekes Judit és Kökényesi Imre cikke számol be a tapasztalatokról.

A matematika világnapjának megünneplésére a Szegedi Tudományegyetem Bolyai Intézetének legnagyobb termében került sor, ahol csak pótszékek és állóhelyek segítségével fért be a 150 fős közönség. A szegedi egyetemi tanárok, kutatók mellett idén egy „országos legendát” is sikerült elcsábítanunk, a 98 éves Obádovics Gyulát. Neve főleg a generációk által használt, 1956-ban írt könyvéről híres, pedig amellett, hogy most is kutat, ír és olvas komoly matematikát, sőt verseskötete, regényei jelentek meg – tudósít Győrffy Lajos.

A kecskeméti MATEGYE Alapítvány a 2020-ban megjelent Hibás feladatmegoldások az általános iskolában című könyvének folytatásaként adta ki 2025-ben Orosz Gyula: Hibás feladatmegoldások a középiskolában című munkáját. Mindkét mű rendhagyó módon közelíti meg a matematikai gyakorlást: nem csak az „egyik helyes” útvonalat, azaz a megoldást mutatják be, hanem a tanulók és tanárok számára egyaránt rendkívül értékes hibaanalízist kínálnak.

Néhány nappal 99. születsésnapja után, 2025. május 16-án elhunyt Lax Péter, a világhírű magyar származású amerikai matematikus. Hatása a 20. század matematikájára egyedülálló és példaértékű volt, amiért 2005-ben Abel-díjat kapott. 15 évesen hagyta el Magyarországot, de még idős korában is hazalátogatva, magyarul – akcentus nélkül – tartotta meg előadásait. Faragó István emlékezik meg róla, de aki szakmai vagy személyes életútját mélyebben is meg szeretné ismerni, annak további hivatkozásokat is ajánlunk.

Kéri Gerzson: „Vázlatok három tantárgy diákolimpiáinak a versenyzőiről, valamint az országos versenyek legjobbjairól 1894–2024” címmel megjelent munkájának és az azt megelőző „Hatvanhat év legtehetségesebb matekos diákjai. A matematikai diákolimpiák magyar versenyzői 1959–2024” saját kiadású könyvének nemrég megjelent, 2025-ig kiterjesztett online változatáról Oláh Vera írt könyvajánlót.

A 2025. április 4–6. között Debrecenben megrendezett Matematika és Informatika Didaktikai Kutatások konferencia, a MIDK 2025 elsődleges célja az volt, hogy lehetőséget biztosítson arra, hogy a magyarországi és a határon túli, matematika- és informatikadidaktikával foglalkozó már elismert és fiatalabb kutatók is találkozzanak, beszámolhassanak aktuális kutatásaikról, tanácsokat, ötleteket kapjanak, bekapcsolódjanak egymás munkájába, közös programot indítsanak. Képünk András Szilárd kolzsvári egyetemi docens előadásán készült. A konferenciáról a szervezőbizottságból Báró Emőke számolt be.

A váci Boronkay György Műszaki Technikum és Gimnázium egykori diákja, majd tanára és jelenlegi igazgatója, Fábián Gábor jogos büszkeséggel írt le néhány gondolatot iskolája múltjáról, fejlődéséről és tehetséggondozó tevékenységéről. Mára a technikumok között elért matematikai eredményeik kimagaslóak, amint az a történet végén az OKTV-dobogósaik és duplázó döntőseik felsorolásából is látható...

A Møbee nevű kártyajáték szabálya nagyon egyszerű: Csapj fel három lapot a pakliból és keresd meg azt az egyetlen figurát, amelyik mindhármon szerepel! A leggyorsabb játékos nyeri a kört. Az ilyen paklik gyártásához szükséges kombinatorikai struktúrákat tárgyalta Ruff János 2024 márciusi számunkban megjelent írásában. Most további két blokkrendszerre ad konstrukciókat. A második blokkrendszerből „Møbee Twin” kártyapaklik gyárthatók. Hogyan? Megtudhatjuk a cikkből.

2025. február 10-étől 15-éig zajlott le a 16. Romanian Master of Mathematics (RMM) verseny, 16 ország mintegy 100 versenyzőjének részvételével. A magyar versenyzők a kiadott 8 aranyéremből egyet, a 14 ezüstérem közül pedig hármat is megszereztek, így a csapatversenyben Kína  mögött a másodikok lettek, megelőzve az USA, Izrael, Bulgária és Románia csapatait. A csapatvezetők, Lenger Dániel és Kovács Benedek beszámolója következik.