Legyen  egy pozitív egész szám és tegyük fel, hogy van
egy pozitív egész szám és tegyük fel, hogy van  bizottság, melyek mindegyikének
bizottság, melyek mindegyikének  tagja van, továbbá bármely két bizottságnak legfeljebb egy közös tagja. A bizottságok rendelkezésére egyetlen konferenciaterem áll, melyben
tagja van, továbbá bármely két bizottságnak legfeljebb egy közös tagja. A bizottságok rendelkezésére egyetlen konferenciaterem áll, melyben  db szék található. Megoldható-e, hogy mindenkinek állandó helye legyen, azaz egy adott ember az összes olyan bizottság ülésén, melynek tagja, mindig ugyanazon a széken üljön? Ez a probléma nem valamiféle idézet egy konferenciaszervezési prospektusból, hanem1 közérthető megfogalmazása az Erdős–Faber–Lovász sejtésnek, amely Erdős Pál egyik kedvenc sejtése volt és amelynek megoldása kétségkívül 2021 egyik fő matematikai szenzációja. Erdősnek szokása volt pénzjutalmat kitűzni sejtései megoldásáért, melyek nagysága a probléma (általa előzetesen vélt) nehézségétől függött. Ezért a sejtésért eredetileg 50 dollárt kínált, majd kisvártatva 500 dollárra emelte az összeget [4]. Ennek ellenére (vagy épp ezért) több mint 40 évet kellett várni a megoldásra.
db szék található. Megoldható-e, hogy mindenkinek állandó helye legyen, azaz egy adott ember az összes olyan bizottság ülésén, melynek tagja, mindig ugyanazon a széken üljön? Ez a probléma nem valamiféle idézet egy konferenciaszervezési prospektusból, hanem1 közérthető megfogalmazása az Erdős–Faber–Lovász sejtésnek, amely Erdős Pál egyik kedvenc sejtése volt és amelynek megoldása kétségkívül 2021 egyik fő matematikai szenzációja. Erdősnek szokása volt pénzjutalmat kitűzni sejtései megoldásáért, melyek nagysága a probléma (általa előzetesen vélt) nehézségétől függött. Ezért a sejtésért eredetileg 50 dollárt kínált, majd kisvártatva 500 dollárra emelte az összeget [4]. Ennek ellenére (vagy épp ezért) több mint 40 évet kellett várni a megoldásra.
Dong Yeap Kang, Thomas Kelly, Daniela Kühn, Abhishek Methuku és Deryk Osthus oldotta meg a sejtést, amely így már Kang–Kelly–Kühn–Methuku–Osthus-tétel. Bár az eredmény egyelőre csak kézirat formájában létezik [16], 2021 januárjában töltötték fel az ArXiv kéziratszerverre, tehát nincsen hivatalosan lektorálva, egy ilyen eredménynél elég sokan egyből elolvassák a kéziratot, ha bármi pontatlanság lenne benne, az már kiderült volna. Így pár hónap elteltével nagy bizonyossággal állíthatjuk, hogy a bizonyítás teljes. Az eredmény azóta nagy hullámokat vert, több fontos kombinatorikai blogon és népszerűsítő oldalon írtak róla [1,11,15,18].
Bár elsőre talán nem látszik, de a magyar szálat a történetben nem csak Erdős Pál és Lovász László jelentik, hanem Abhishek Methuku is, aki 2019-ben a Central European University-n szerezte meg PhD-ját, témavezetői Katona OH Gyula és Győri Ervin voltak, és sok magyar kombinatorikussal dolgozott együtt, például ezen írás szerzőivel is számos közös cikke van.
1. Történet, bevezető
Erdős Pál, Vance Faber és Lovász László 1972 szeptemberében mondta ki a sejtést Faber lakásában, egy teadélutánon. Ők hárman egy pár héttel korábbi, hipergráfokról szóló konferenciáról beszélgettek és úgy találták, hogy érdemes lenne gráfok színezésével kapcsolatos eredményeket lineáris hipergráfokra kiterjeszteni. Ekkor jutottak el azon könnyen megfogalmazható sejtésig, amit  -halmaz problémának neveztek:
-halmaz problémának neveztek:
( -halmaz probléma.) Legyen
-halmaz probléma.) Legyen  egy pozitív egész szám és legyen adott
egy pozitív egész szám és legyen adott  darab
darab  elemű halmaz úgy, hogy bármelyik kettőnek legfeljebb egy közös eleme van. Ekkor ki lehet színezni az elemeket
elemű halmaz úgy, hogy bármelyik kettőnek legfeljebb egy közös eleme van. Ekkor ki lehet színezni az elemeket  színnel úgy, hogy mindegyik halmazban előfordul mindegyik szín.
színnel úgy, hogy mindegyik halmazban előfordul mindegyik szín.
Úgy döntöttek, másnap is találkoznak, hogy kidolgozzák a megoldást. Ez azonban nem sikerült: a probléma bonyolultabbnak bizonyult a vártnál.
1.1. Hogy merült fel a kérdés, változatok egy sejtésre
Hogy a problémát motiválni tudjuk, visszamegyünk az időben, egészen 1964-ig, az ún. Vizing-tétel [25] megszületéséig, melynek kimondása előtt kis fogalmi kitérőt teszünk és bevezetünk pár dolgot.
Egy (egyszerű) gráf egy ponthalmazból és egy élhalmazból áll: az élek pontpároknak felelnek meg; némelyik pontpár élt formál, mások esetleg nem. Egy adott pont fokszámán azt a számot értjük, ahány él tartalmazza az adott pontot.
Párosításnak nevezzük élek egy olyan halmazát egy gráfban, mely halmaz bármely két különböző élére igaz, hogy nincs közös végpontjuk. Például minden egyes él külön-külön egy-egy párosítás, de persze az igazán érdekes az, ha egy gráfban nagyobb párosításokat tudunk találni. Mivel a párosítások egy elég egyszerű struktúrát alkotnak, alapvető kérdés, hogyan tudunk párosítások uniójára (azaz egyszerűbb részekre) felbontani egy gráfot. Nyilván, ha egyesével élekre bontjuk, akkor kapunk egy felbontást, ami nem igazán tartalmaz új információt, de az például egy jó kérdés, hogy mi az a legkisebb szám, ahány darab párosítás uniójára felbontható egy gráf. Ez a kérdés ekvivalens azzal, hogy szeretnénk meghatározni azt a minimális számot, ahány színnel ki lehet egy gráf éleit színezni úgy, hogy azonos színű éleknek ne legyen közös pontjuk, hiszen egyértelmű kapcsolat van a(z ilyen feltételt kielégítő) színosztályok és a párosítások között. Ezt a számot a gráf kromatikus indexének nevezzük. Egyszerű észrevétel, hogy legalább maximális fokszámnyi színre szükségünk lesz a színezéshez (hiszen van olyan pont a gráfban, amihez kapcsolódó élek színezéséhez legalább ennyi szín kell). Vizing 1964-ben látta be, hogy ennyi majdnem elég is, pontosabban hogy egy gráf kromatikus indexe vagy egyenlő a maximális fokszámmal, vagy a maximális fokszámnál eggyel nagyobb.
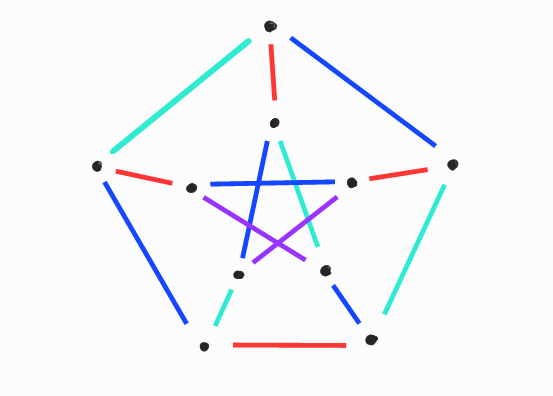
Rövid példaként az élszínezésre lássuk a következő, ún. Petersen-gráfot. Látható, hogy legalább 3 szín kell a színezéséhez fokszám okokból. Hogy 3 szín nem elég, annak a bizonyítását az olvasóra bízzuk. (Aki nem boldogul vele, a következő helyen talál egy rövid megoldást: [22])
Vizing tételének egy hipergráfokra vonatkozó általánosítását kereste Erdős, Faber és Lovász 1972-ben. A hipergráfok a gráfok általánosításai: élek helyett ún. hiperéleket tekintünk, mely hiperélek a ponthalmazok részhalmazainak felelnek meg, tehát kettőnél több pont is tartozhat egy hiperélhez (de akár egy is). Egy hipergráfot 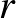 -uniformnak mondunk, ha minden hiperél mérete pontosan
-uniformnak mondunk, ha minden hiperél mérete pontosan 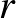 , és lineárisnak, ha bármely két hiperélnek legfeljebb egy közös pontja van. Hipergráf hiperéleit is színezhetjük, és a kromatikus indexe ugyanúgy bevezethető: úgy akarjuk színezni a hiperéleket, hogy semelyik pont ne legyen két egyforma színű hiperélben. Egy hipergráf kromatikus indexe a legkevesebb szín amivel ez megoldható. Most már kimondhatjuk az Erdős–Faber–Lovász sejtés újabb verzióját:
, és lineárisnak, ha bármely két hiperélnek legfeljebb egy közös pontja van. Hipergráf hiperéleit is színezhetjük, és a kromatikus indexe ugyanúgy bevezethető: úgy akarjuk színezni a hiperéleket, hogy semelyik pont ne legyen két egyforma színű hiperélben. Egy hipergráf kromatikus indexe a legkevesebb szín amivel ez megoldható. Most már kimondhatjuk az Erdős–Faber–Lovász sejtés újabb verzióját:
Élszínezős változat. Egy  pontú lineáris hipergráf kromatikus indexe legfeljebb
pontú lineáris hipergráf kromatikus indexe legfeljebb  .
.
Kang, Kelly, Kühn, Methuku and Osthus ezt a formáját használták a sejtésnek, ezért mi is erre fogunk majd a későbbiekben hivatkozni. De térjünk még vissza az eredeti  -halmaz probléma más változataihoz. Hipergráfoknak nem csak az éleit, hanem a pontjait is színezhetjük.
-halmaz probléma más változataihoz. Hipergráfoknak nem csak az éleit, hanem a pontjait is színezhetjük.
Pontszínezős változat. Egy  élű
élű  -uniform lineáris hipergráfnak kiszínezhetjük a pontjait
-uniform lineáris hipergráfnak kiszínezhetjük a pontjait  színnel úgy, hogy minden élben feltűnik minden szín.
színnel úgy, hogy minden élben feltűnik minden szín.
A két változat kimondása után gondoljunk meg két dolgot:
 Egyrészt, hogy a 2 változat ugyanaz. Ez az ún. dualitás következménye: egy
Egyrészt, hogy a 2 változat ugyanaz. Ez az ún. dualitás következménye: egy 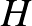 hipergráf duálisa az a másik
hipergráf duálisa az a másik 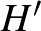 hipergráf, melyben a pontok az eredeti hiperélek, a hiperélek pedig az eredeti pontok és a tartalmazások megfordulnak. Könnyen látható, hogy így megkaphatjuk az egyik feltételből a másikat, míg élszínezésből pontszínezés lesz és vice versa.
hipergráf, melyben a pontok az eredeti hiperélek, a hiperélek pedig az eredeti pontok és a tartalmazások megfordulnak. Könnyen látható, hogy így megkaphatjuk az egyik feltételből a másikat, míg élszínezésből pontszínezés lesz és vice versa.
 Másrészt azt is gondoljuk meg, hogy a linearitásra valóban szükség van a sejtés állításában. Ezt az alábbi hipergráf mutatja (a pontszínezős változatot vesszük): legyen a ponthalmaza
Másrészt azt is gondoljuk meg, hogy a linearitásra valóban szükség van a sejtés állításában. Ezt az alábbi hipergráf mutatja (a pontszínezős változatot vesszük): legyen a ponthalmaza 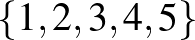 míg a hiperélek halmaza
míg a hiperélek halmaza 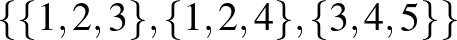 . Könnyen látható, hogy nem lehet 3 színnel megszínezni ezen hipergráf pontjait, hogy minden hiperélben szerepeljen minden színű pont.
. Könnyen látható, hogy nem lehet 3 színnel megszínezni ezen hipergráf pontjait, hogy minden hiperélben szerepeljen minden színű pont.
Kimondunk egy harmadik változatot is, amely fel szokott bukkanni az irodalomban és fő előnye, hogy gráfproblémaként fogalmazza meg a sejtést. Sőt, a színezés amiről itt szó van, a legalapvetőbb, legtöbbet vizsgált színezés. A sejtés előző két változatával való ekvivalenciájának bizonyítását az olvasóra bízzuk.
Teljes gráfos változat. Vegyünk  darab teljes gráfot, amiknek mind
darab teljes gráfot, amiknek mind  pontja van. Rakjuk ezeket egy közös
pontja van. Rakjuk ezeket egy közös 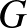 gráfba úgy, hogy bármelyik kettőnek az
gráfba úgy, hogy bármelyik kettőnek az  teljes gráf közül legfeljebb egy közös pontja van. Ekkor
teljes gráf közül legfeljebb egy közös pontja van. Ekkor 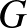 pontjai kiszínezhetők
pontjai kiszínezhetők  színnel úgy, hogy minden él két végpontja különböző színű.
színnel úgy, hogy minden él két végpontja különböző színű.
1.2. Hipergráfok, melyeknek  a kromatikus indexe
a kromatikus indexe
Ugyan érződik, hogy lehetnek olyan hipergráfok párosításával kapcsolatos problémák, amik esetleg nehezebbek a gráfváltozatnál2, a konkrét fő oka annak, hogy ez a sejtés ilyen nehéznek bizonyult, az lehet, hogy többféle hipergráf van, ami teljesíti a feltételeket és pontosan  a kromatikus indexe. Ha csak egyféle ilyen konstrukció lenne, akkor lehetne abban bízni (és gyakran ez a helyzet hasonló problémáknál), hogy az olyan hipergráfok, amiknek közel
a kromatikus indexe. Ha csak egyféle ilyen konstrukció lenne, akkor lehetne abban bízni (és gyakran ez a helyzet hasonló problémáknál), hogy az olyan hipergráfok, amiknek közel  a kromatikus indexe, azok szerkezetüket tekintve mind hasonlóak az egyedi konstrukcióhoz, és ezzel az információval már lehet valamit kezdeni. Csakhogy itt nem ez a helyzet, egymástól lényegesen eltérő példák vannak.
a kromatikus indexe, azok szerkezetüket tekintve mind hasonlóak az egyedi konstrukcióhoz, és ezzel az információval már lehet valamit kezdeni. Csakhogy itt nem ez a helyzet, egymástól lényegesen eltérő példák vannak.
Nézzük ezeket a konstrukciókat.
1. Az egyik konstrukció az  pontú teljes gráf: ez egy lineáris hipergráf, és ha
pontú teljes gráf: ez egy lineáris hipergráf, és ha  páratlan, akkor
páratlan, akkor  a kromatikus indexe.
a kromatikus indexe.
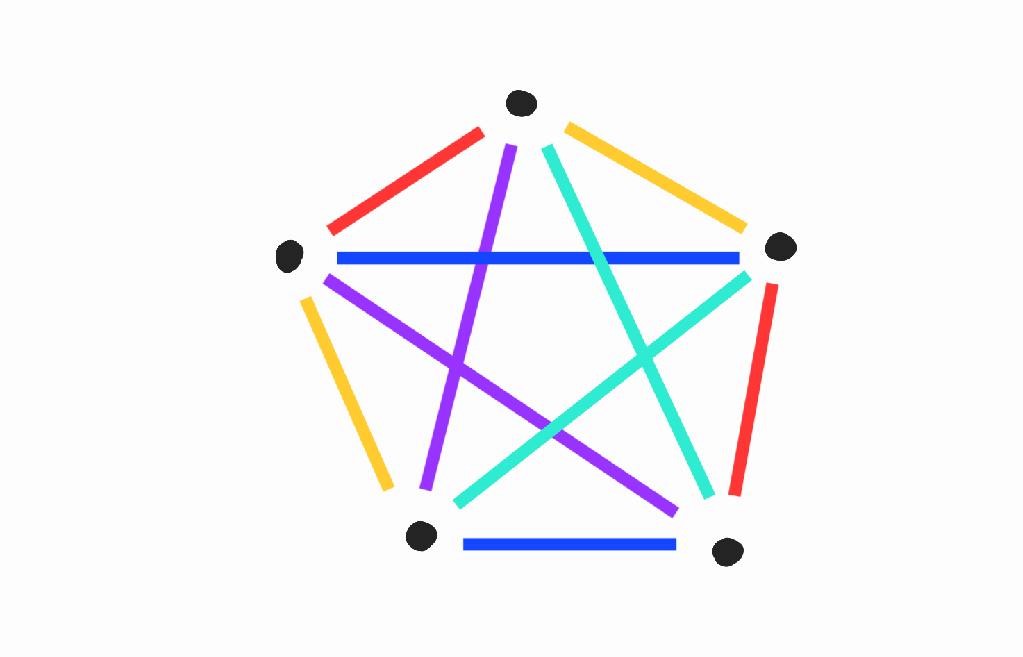
 pontja és
pontja és  hiperéle (egyenese) van, és bármely két egyenes metszi egymást, tehát különböző színt kell, hogy kapjon.
hiperéle (egyenese) van, és bármely két egyenes metszi egymást, tehát különböző színt kell, hogy kapjon.
3. A harmadik konstrukció kevésbé szabályos: veszünk egy 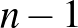 pontú hiperélt, és az összes két pontú élt ami tartalmazza az
pontú hiperélt, és az összes két pontú élt ami tartalmazza az  -edik pontot.
-edik pontot.
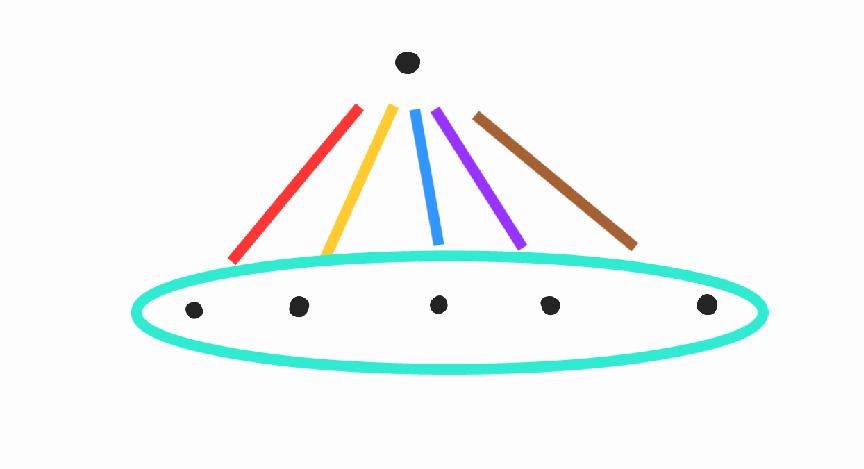
Kang, Kelly, Kühn, Methuku and Osthus azt is belátta, hogy minden hipergráfhoz ami ezektől lényegesen különbözik,  -nél jóval kevesebb szín elegendő. Erre még visszatérünk (ahhoz viszont, hogy pontosan mi számít „lényeges különbségnek” és „jóval kevesebbnek”, az eredeti kéziratot [16] kell megnézni).
-nél jóval kevesebb szín elegendő. Erre még visszatérünk (ahhoz viszont, hogy pontosan mi számít „lényeges különbségnek” és „jóval kevesebbnek”, az eredeti kéziratot [16] kell megnézni).
2. Korábbi eredmények
A sejtést 1972 óta sokan vizsgálták, korábban is született több előrelépés a megoldása felé, ezekből gyűjtünk össze pár fontosabb eredményt:
 Chang és Lawler [3] 1988-ban
Chang és Lawler [3] 1988-ban 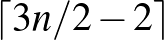 -es felső korlátot adott
-es felső korlátot adott  pontú lineáris hipergráfok kromatikus indexére.
pontú lineáris hipergráfok kromatikus indexére.
 Kahn [13] 1992-ben közel került a sejtés bizonyításához: egy olyan felső korlátot mutatott a kromatikus indexre, ami
Kahn [13] 1992-ben közel került a sejtés bizonyításához: egy olyan felső korlátot mutatott a kromatikus indexre, ami  -nel osztva 1-hez tart.
-nel osztva 1-hez tart.
 Olyan hipergráfok esetén, ahol a minimum fokszám legalább
Olyan hipergráfok esetén, ahol a minimum fokszám legalább 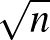 , Sanchez-Arroyo 2008-ban belátta a sejtést [24].
, Sanchez-Arroyo 2008-ban belátta a sejtést [24].
 Faber [5] 2010-ben azt vizsgálta, ha az
Faber [5] 2010-ben azt vizsgálta, ha az  pontú lineáris hipergráfban minden pontnak a foka pontosan
pontú lineáris hipergráfban minden pontnak a foka pontosan 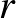 .
.
A terület mostanában is elég aktív volt, például 2019 publikált Faber és Harris egy cikket [6], melyben belátták, hogy ha minden hiperél „közepes” nagyságú (ezt nem mondjuk ki pontosabban, a cikkben megtalálható a pontos állítás), akkor  -nél (konstansszor) kevesebb szín is elég a pontok kiszínezéséhez. Illetve megemlíthetjük Janzer Olivér és Nagy Zoltán 2019-es munkáját [12], melyben a kombinatorikus Nullstellensatz-cal hozták összefüggésbe a sejtést.
-nél (konstansszor) kevesebb szín is elég a pontok kiszínezéséhez. Illetve megemlíthetjük Janzer Olivér és Nagy Zoltán 2019-es munkáját [12], melyben a kombinatorikus Nullstellensatz-cal hozták összefüggésbe a sejtést.
A sejtés történetéről további fejleményeket találhat az olvasó a következő helyeken: [9,21,23].
3. Pár szó a bizonyításról
A bizonyítás természetesen túl összetett ahhoz, hogy részleteibe belemehetnénk ebben a cikkben, csak megemlítünk néhány fontos összetevőt.
A szerzők több olyan módszert kombinálnak, amik önmagukban is áttörést jelentettek és fontos sejtések megoldásához vezettek korábban. Az egyik az úgynevezett Rödl nibble3, amelyet Rödl először az ún. Erdős–Hanani sejtés megoldása során használt. A másik az ún. absorption4 method, amely hatalmas karriert futott be az elmúlt évtizedben és a Daniela Kühn és Deryk Osthus vezette birminghami iskola egyik védjegyévé vált. Segítségével több olyan problémát sikerült pontosan megoldani, amik aszimptotikusan korábban megvoltak
Alább részletesebben is írunk erről a két módszerről. Emellett ahol lehet, a szerzők próbálnak hipergráfok helyett gráfokat színezni, így tudják használni a gráfszínezésekről meglévő sokkal átfogóbb ismereteket.
3.1. A bizonyítás vázlata
A bizonyítás során egy meglehetősen logikus sorrendből indulnak ki: először kiszínezik a nagy hiperéleket, aztán a közepeseket, majd a legkisebbeket. Azért logikus ez a sorrend, mert minél nagyobb a hiperél, annál több pontnál jelent ez megkötést az egyéb hiperélek színére vonatkozóan. Valójában egy 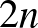 -es felső korlát már rögtön következik ha a hiperéleken nem-növekvő sorrendben végigmegyünk: ha egy
-es felső korlát már rögtön következik ha a hiperéleken nem-növekvő sorrendben végigmegyünk: ha egy 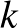 méretű hiperél a következő, akkor a
méretű hiperél a következő, akkor a 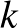 pontján mind legfeljebb
pontján mind legfeljebb 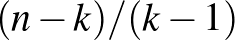 korábbi hiperél megy át, hiszen azoknak a hiperéleknek a mérete mind legalább
korábbi hiperél megy át, hiszen azoknak a hiperéleknek a mérete mind legalább 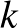 , és se egymást, se a soron következő hiperélünket nem metszik máshol. Tehát legfeljebb
, és se egymást, se a soron következő hiperélünket nem metszik máshol. Tehát legfeljebb 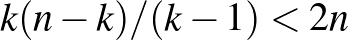 hiperél van amit már kiszíneztünk, azaz legfeljebb ennyi szín van amit nem használhatunk a hiperélünkhöz, vagyis van olyan szín amit igen. Ezt a fajta színezési algoritmust mohónak nevezzük, mert a soron következő hiperélt úgy színezzük ki, hogy nem gondolunk a jövőre, lecsapunk egy elérhető színre. Ahhoz hogy fele ennyi színnel kiszínezzük a hiperéleket, persze okosabban kell megtervezni, hogy mit csinálunk.
hiperél van amit már kiszíneztünk, azaz legfeljebb ennyi szín van amit nem használhatunk a hiperélünkhöz, vagyis van olyan szín amit igen. Ezt a fajta színezési algoritmust mohónak nevezzük, mert a soron következő hiperélt úgy színezzük ki, hogy nem gondolunk a jövőre, lecsapunk egy elérhető színre. Ahhoz hogy fele ennyi színnel kiszínezzük a hiperéleket, persze okosabban kell megtervezni, hogy mit csinálunk.
3.2. Nagy, közepes, kicsi
A nagy hiperélek színezésében egy fontos ötlet segít: vegyük azt a gráfot, aminek a pontjai az eredeti hipergráf hiperélei, és két pont akkor van összekötve, ha a hiperéleknek van közös pontja. Ezzel a hiperélszínezés helyett egy szokványos pontszínezésünk van gráfokon.
Közepes méretű hiperélekkel kapcsolatban többet mutatnak meg. Fentebb mutattunk három példát, ahol a kromatikus index pontosan  , és mindegyikben csak nagyon kicsi és/vagy nagyon nagy hiperélek vannak. Ez nem csak ezeknél a példáknál van így, hanem tényleg nagyobb a mozgástér. Valójában azt is megmutatták a sejtés megoldása mellett, hogy vagy van egy pont amit majdnem minden hiperél tartalmaz, mint az első és harmadik konstrukcióban, vagy majdnem minden él majdnem
, és mindegyikben csak nagyon kicsi és/vagy nagyon nagy hiperélek vannak. Ez nem csak ezeknél a példáknál van így, hanem tényleg nagyobb a mozgástér. Valójában azt is megmutatták a sejtés megoldása mellett, hogy vagy van egy pont amit majdnem minden hiperél tartalmaz, mint az első és harmadik konstrukcióban, vagy majdnem minden él majdnem  méretű, mint a második konstrukcióban, vagy a kromatikus index lényegesen kisebb mint
méretű, mint a második konstrukcióban, vagy a kromatikus index lényegesen kisebb mint  .
.
Amikor a nagy és közepes hiperéleket kiszíneztük, még mindig nem használtuk el mind az  színt. A kicsi élek egy részét a már használt színekkel tudjuk kiszínezni, a maradékban pedig már csak két pontot tartalmazó hiperélek vannak. Ezekhez pedig a fennmaradó színeket használjuk, meg persze Vizing tételét.
színt. A kicsi élek egy részét a már használt színekkel tudjuk kiszínezni, a maradékban pedig már csak két pontot tartalmazó hiperélek vannak. Ezekhez pedig a fennmaradó színeket használjuk, meg persze Vizing tételét.
Menjünk bele egy kicsit mélyebben, hogyan is színezzük a hiperéleket. A legtöbb esetben véletlenszerűen. Talán meglepő lehet, hogy a bizonyítás nagy mértékben használ véletlen módszereket. Eddig nem említettünk ilyesmit, a sejtésben sem voltak valószínűségek, és a megoldás sem csak nagy valószínűséggel igaz, hanem minden hipergráfra. De mára a véletlen alkalmazása egy standard módszer a kombinatorikában. A legegyszeűbb alkalmazása a véletlennek így néz ki: keresünk valamilyen matematikai objektumot (jelen esetben egy hiperélszínezést legfeljebb  színnel), és választunk egyet véletlenszerűen. Kiszámoljuk mennyi az esélye annak, hogy az teljesíti a plusz feltételeket (jelen esetben azt, hogy ha két hiperélnek van közös pontja, akkor különböző a színük). Vagy ha kiszámolni nem tudjuk, legalább adunk rá egy becslést. Ha ugyanis ez az esély nagyobb mint nulla százalék, az azt jelenti hogy van több mint nulla megfelelő színezés, és ennél mi nem is akartunk többet.
színnel), és választunk egyet véletlenszerűen. Kiszámoljuk mennyi az esélye annak, hogy az teljesíti a plusz feltételeket (jelen esetben azt, hogy ha két hiperélnek van közös pontja, akkor különböző a színük). Vagy ha kiszámolni nem tudjuk, legalább adunk rá egy becslést. Ha ugyanis ez az esély nagyobb mint nulla százalék, az azt jelenti hogy van több mint nulla megfelelő színezés, és ennél mi nem is akartunk többet.
Persze erre a problémára nem ilyen egyszerű a megoldás, hanem sokkal komplikáltabb módon használjuk a véletlent, például a már említett Rödl nibble-nél. Jóllehet az is egy egyszerű ötletre épül. Vegyünk néhány hiperélt amik nem tartalmaznak közös pontot, véletlenszerűen. Ezután tegyük félre a hiperéleket meg a pontjaikat is, és a maradékon vegyünk még néhány hiperélt, és így tovább. Így apró harapásokkal veszünk ki egy hiperélhalmazt, ami megfelelő lesz egy színosztálynak. Aztán visszatesszük a félretett pontokat, és a maradék hiperélekből kiharapdálunk egy másik színosztályt is, és így tovább.
A másik fejlett technika amit alkalmaznak az absorption. A kis hiperélek egy véletlenszerűen kiválasztott részét félretesszük. Amikor a nagy és közepes méretű hiperélekkel végeztünk, akkor még  -nél kevesebb színt használtunk csak fel, és ezekből is néhány színt még fel lehet használni a kis hiperélekhez. Ezt úgy csináljuk, hogy bizonyos pontokra (a nagy fokúakra) azt akarjuk hogy minél több olyan szín legyen az őket tartalmazó hiperéleken, amit már felhasználtunk. Ez azért fontos, mert a nagyfokú pontoknál sok szín kell hogy felbukkanjon az őket tartalmazó hiperélekben. A félretett kis hiperélekből tehát úgy választunk a már elkezdett színekbe, hogy minél több nagyfokú pontot elnyeljenek ezek a színosztályok, innen az elnevezés.
-nél kevesebb színt használtunk csak fel, és ezekből is néhány színt még fel lehet használni a kis hiperélekhez. Ezt úgy csináljuk, hogy bizonyos pontokra (a nagy fokúakra) azt akarjuk hogy minél több olyan szín legyen az őket tartalmazó hiperéleken, amit már felhasználtunk. Ez azért fontos, mert a nagyfokú pontoknál sok szín kell hogy felbukkanjon az őket tartalmazó hiperélekben. A félretett kis hiperélekből tehát úgy választunk a már elkezdett színekbe, hogy minél több nagyfokú pontot elnyeljenek ezek a színosztályok, innen az elnevezés.
A fentebb leírtak, tehát a Rödl nibble, utána absorption, és utána Vizing tétele, csak a hipergráfok nagy részére működik. Utána nagyon alaposan meg kell vizsgálni a kimaradó hipergráfokat is a bizonyítás befejezéséhez.
Az érdeklődő olvasó eggyel részletesebb bizonyításvázlatot találhat a kézirat [16] második fejezetében illetve a következő youtube linkeken:
 Abhishek Methuku előadásának felvétele: [20] (csak a diák: [19]).
Abhishek Methuku előadásának felvétele: [20] (csak a diák: [19]).
 Thomas Kelly előadásának felvétele: [17].
Thomas Kelly előadásának felvétele: [17].
4. Felmerülő további kérdések
Bár a bizonyításuk egy fontos kérdést megválaszolt, több kérdés nyitva maradt a témakörben. Az első a bizonyításhoz kapcsolódóan, hogy igaz-e a sejtés minden 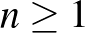 -re? A szerzők a kéziratban nem adnak felső becslést arra az
-re? A szerzők a kéziratban nem adnak felső becslést arra az 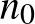 -ra, ahonnan kezdve a bizonyítás működik.
-ra, ahonnan kezdve a bizonyítás működik.
A következő kapcsolódó nyitott kérdés az ún. Berge–Füredi–Meyniel sejtés, amit az említett három matematikus egymástól függetlenül fogalmazott meg [2,7]. Legyen 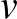 egy hipergráf pontja, és jelöljük
egy hipergráf pontja, és jelöljük 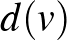 -vel a
-vel a 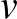 -t tartalmazó hiperélek úniójának méretét. A sejtés szerint egy hipergráf kromatikus indexe legfeljebb a legnagyobb
-t tartalmazó hiperélek úniójának méretét. A sejtés szerint egy hipergráf kromatikus indexe legfeljebb a legnagyobb 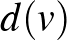 . Mivel
. Mivel 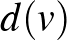 legfeljebb a pontok száma, ez erősebb mint az Erdős–Faber–Lovász sejtés. Ha egy gráfot nézünk,
legfeljebb a pontok száma, ez erősebb mint az Erdős–Faber–Lovász sejtés. Ha egy gráfot nézünk, 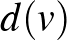 a
a 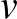 fokszáma plusz egy, tehát ez a sejtés a Vizing tételnek is általánosítása.
fokszáma plusz egy, tehát ez a sejtés a Vizing tételnek is általánosítása.
De az Erdős–Faber–Lovász-sejtés analogonjait kimondhatjuk másfajta színezésekre is, egy példa az ún. listaszínezés. Itt minden hiperélhez adott egy lista  színből, és abból kell kiválasztani hogy milyenre színezzük (az elvárás továbbra is az, hogy egy pontot tartalmazó hiperélek színe különböző legyen). Abban a speciális esetben, ha minden hiperélhez ugyanaz a lista, akkor visszakapjuk az eredeti problémát. Mivel a színezésre vonatkozó megkötések olyanok, hogy bizonyos hiperéleket különböző színűre akarunk színezni, azt is gondolhatnánk hogy csak segít ha eleve különböző színek vannak a listákban. De ez nem igaz, bizonyos hipergráfokhoz vannak olyan listák amik a kromatikus indexnél sokkal több színt tartalmaznak, és mégse lehet kiválasztani megfelelő színeket. Az Erdős–Faber–Lovász sejtés listás változata még nyitott kérdés.
színből, és abból kell kiválasztani hogy milyenre színezzük (az elvárás továbbra is az, hogy egy pontot tartalmazó hiperélek színe különböző legyen). Abban a speciális esetben, ha minden hiperélhez ugyanaz a lista, akkor visszakapjuk az eredeti problémát. Mivel a színezésre vonatkozó megkötések olyanok, hogy bizonyos hiperéleket különböző színűre akarunk színezni, azt is gondolhatnánk hogy csak segít ha eleve különböző színek vannak a listákban. De ez nem igaz, bizonyos hipergráfokhoz vannak olyan listák amik a kromatikus indexnél sokkal több színt tartalmaznak, és mégse lehet kiválasztani megfelelő színeket. Az Erdős–Faber–Lovász sejtés listás változata még nyitott kérdés.
Irodalomjegyzék
[2] C. Berge. On the chromatic index of a linear hypergraph and the Chvatal conjecture, in: Combinatorial Mathematics: Proceedings of the Third International Conference, New York, 1985, Ann. New York Acad. Sci., 555, (1989) 40–44.
[3] W. I. Chang, E. L. Lawler. Edge coloring of hypergraphs and a conjecture of Erdős, Faber, Lovász, Combinatorica, 8(3), (1988) 293–295.
[4] P. Erdős. On the combinatorial problems which I would most like to see solved, Combinatorica, 1, (1981) 25–42.
[5] V. Faber, The Erdős-Faber-Lovász conjecture – the uniform regular case, J. Comb. 1(2), (2010) 113–120.
[6] V. Faber, D. G. Harris. Edge-coloring linear hypergraphs with medium-sized edges, Random Structures & Algorithms, 55(1), (2019) 153–159.
[7] Z. Füredi. The chromatic index of simple hypergraphs, Graphs Comb., 2, (1986) 89–92.
[8] S. Glock, D. Kühn, A. Lo, D. Osthus, (2016). The existence of designs via iterative absorption. arXiv preprint arXiv:1611.06827.
[9] Gócza Gergely, BSc dolgozat
[10] L. Haddad, C. Tardif. A clone-theoretic formulation of the Erdős-Faber-Lovász conjecture. Discussiones Mathematicae Graph Theory, 24(3), (2004) 545–549.
[11] K. Houston-Edwards. Mathematicians Settle Erdős Coloring Conjecture, Quanta magazine, 2021.
[12] Oliver Janzer, Zoltán Lóránt Nagy. Coloring linear hypergraphs: the Erdős–Faber–Lovász conjecture and the Combinatorial Nullstellensatz, Designs, Codes and Cryptography, 10.1007/s10623-021-00859-7, (2021).
[13] J. Kahn. Coloring nearly-disjoint hypergraphs with 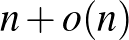 colors, J. Combin. Theory Ser. A, 59(2), (1992) 31–39.
colors, J. Combin. Theory Ser. A, 59(2), (1992) 31–39.
[14] J. Kahn, P. D. Seymour. A fractional version of the Erdős-Faber-Lovász conjecture. Combinatorica, 12(2), (1992) 155–160.
[15] Gil Kalai. To cheer you up in difficult times 17: Amazing! The Erdős-Faber-Lovász conjecture (for large  ) was proved by Dong Yeap Kang, Tom Kelly, Daniela Kühn, Abhishek Methuku, and Deryk Osthus!
) was proved by Dong Yeap Kang, Tom Kelly, Daniela Kühn, Abhishek Methuku, and Deryk Osthus!
[16] Dong Yeap Kang, Tom Kelly, Daniela Kühn, Abhishek Methuku and Deryk Osthus. A proof of the Erdős-Faber-Lovász conjecture, arXiv preprint, arXiv:2101.04698, 2021
[18] R. J. Lipton. Closing an Erdős Problem.
[19] Abhishek Methuku előadásának diái.
[20] Abhishek Methuku előadása.
[21] Nagy Gergely, MSc dolgozat.
[22] R. Naserasr, R. Skrekovski. The Petersen graph is not 3-edge-colorable—a new proof. Discrete mathematics, 268(1–3), (2003) 325–326.
[23] D. Romero, A. Sánchez-Arroyo. Advances on the Erdős-Faber-Lovász conjecture. Oxford Lecture Series in Mathematics and Its Application, 34, 272, 2007.
[24] A. Sánchez-Arroyo. The Erdős–Faber–Lovász conjecture for dense hypergraphs. Discrete Mathematics, 308(5–6), (2008) 991–992.
[25] V. G. Vizing. On an estimate of the chromatic class of a 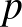 -graph. Discret Analiz, 3, (1964) 25–30.
-graph. Discret Analiz, 3, (1964) 25–30.
Lábjegyzetek
1 Lucien Haddadtól és Claude Tardiftól [10] származó- 2 Azt, hogy hipergráfokra a párosítással kapcsolatos kérdések esetleg sokkal bonyolultabbak lehetnek, alátámasztja az a tény is, hogy Karp szintén 1972-ben előállt 21 nehéz (ún. NP-teljes) problémával, amik között az egyik egy bizonyos 3-uniform hipergráfban a maximális párosítás kiválasztása, ami gráf esetben egy könnyebb kérdés.
- 3 a nibble harapást jelent, de valahogy furán hangzik, hogy Rödl harapás
- 4 elnyelés, felszívás
Gerbner Dániel, Vizer Máté
Rényi Alfréd Matematikai Kutatóintézet









