Az emberiséget hosszú idő óta elbűvölik a különféle szimmetriákat megjelenítő, ismétlődő motívumok. Bolyai János (1802–1860) magyar matematikus és hadmérnök 1823. évi felfedezése, a hiperbolikus geometria megszületése fordulópontot hozott a 19. század matematikájában. Ez a felfedezés sokkal gazdagabb mintázatokat tett lehetővé. Közülük néhányat a holland grafikus, Maurits Cornelis Escher (1898–1972) népszerűsített a híres Circle Limit (Körhatár) fametszet-sorozatában, amelyen a Poincaré-féle körmodellt csempézte ki periodikus mintákkal. A hiperbolikus sík körmodellje nevét Jules Henri Poincaréről (1854–1912) kapta. Számítógép segítségével nem nehéz escher-szerű képeket létrehozni. Szimmetriáról hagyományosan az euklideszi transzformációk – eltolás, forgatás, tükrözés – alkalmazásakor beszélünk. Szimmetria azonban olyan leképezések alkalmazása során is előáll, mint a Möbius-transzformációk, amelyekkel torzítás, nyújtás, csavarás valósítható meg.  -vel jelölve a komplex számok halmazát, az
-vel jelölve a komplex számok halmazát, az
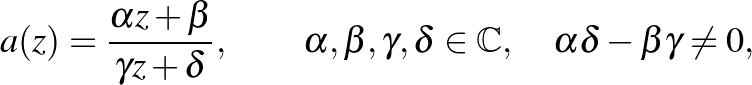
alakú leképezést, ahol 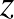 a
a 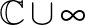 Riemann-gömb eleme, Möbius-transzformációnak nevezzük, August Ferdinand Möbius (1790–1868) emlékére. A Riemann-gömb Georg Friedrich Bernhard Riemann (1826–1866) nevét őrzi. Az ilyen transzformációk az
Riemann-gömb eleme, Möbius-transzformációnak nevezzük, August Ferdinand Möbius (1790–1868) emlékére. A Riemann-gömb Georg Friedrich Bernhard Riemann (1826–1866) nevét őrzi. Az ilyen transzformációk az  alakú mátrixokkal reprezentálhatók. Nem távolságtartók, de megőrzik a szögeket és a Riemann-gömb bármely körét a Riemann-gömb egy körére képezik le (lásd [1] Állítás 8.2, 34. o.). Továbbá előállnak a
alakú mátrixokkal reprezentálhatók. Nem távolságtartók, de megőrzik a szögeket és a Riemann-gömb bármely körét a Riemann-gömb egy körére képezik le (lásd [1] Állítás 8.2, 34. o.). Továbbá előállnak a  ,
, 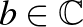 , eltolás, a
, eltolás, a 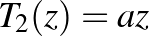 ,
,  , origó körüli forgatva nyújtás és
, origó körüli forgatva nyújtás és 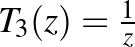 leképezések kompozíciójaként. A
leképezések kompozíciójaként. A 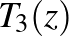 leképezés a
leképezés a 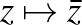 komplex konjugáció, azaz a valós tengelyre való tükrözés és a
komplex konjugáció, azaz a valós tengelyre való tükrözés és a 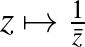 leképezés, azaz az origó középpontú egység sugarú körre vonatkozó inverzió kompozíciója. Az
leképezés, azaz az origó középpontú egység sugarú körre vonatkozó inverzió kompozíciója. Az  mátrix nyoma
mátrix nyoma  . A Möbius-leképezéseket az őket leíró mátrix nyoma szerint a loxodromikus, az elliptikus és a parabolikus leképezések osztályába sorolhatjuk. A loxodromikus leképezéseknek két fixpontjuk van, amelyeket forrás és nyelő fixpontnak nevezzünk. Ilyen leképezések hatására a pontok spirális pályán futnak a leképezés forrás fixpontjából kiindulva a nyelő fixpont felé. Minden loxodromikus leképezés egy
. A Möbius-leképezéseket az őket leíró mátrix nyoma szerint a loxodromikus, az elliptikus és a parabolikus leképezések osztályába sorolhatjuk. A loxodromikus leképezéseknek két fixpontjuk van, amelyeket forrás és nyelő fixpontnak nevezzünk. Ilyen leképezések hatására a pontok spirális pályán futnak a leképezés forrás fixpontjából kiindulva a nyelő fixpont felé. Minden loxodromikus leképezés egy 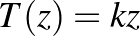 ,
, 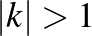 leképezés konjugáltja. A loxodromikus leképezéseket leíró mátrix nyoma egy
leképezés konjugáltja. A loxodromikus leképezéseket leíró mátrix nyoma egy ![$\mathbb{C} \setminus
[-2,2]$](/images/stories/latexuj/2020-11/2020-11-figulaagotakleingyongyok/img16.png) -beli szám. Azokat a Möbius-transzformációkat, amelyeknek egyetlen fixpontjuk van, azaz a forrás és a nyelő fixpontjuk egybeesik, parabolikusnak nevezzük. Minden parabolikus leképezés egy
-beli szám. Azokat a Möbius-transzformációkat, amelyeknek egyetlen fixpontjuk van, azaz a forrás és a nyelő fixpontjuk egybeesik, parabolikusnak nevezzük. Minden parabolikus leképezés egy 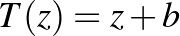 ,
, 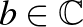 , eltolás konjugáltja. A parabolikus leképezésekhez tartozó mátrix nyoma
, eltolás konjugáltja. A parabolikus leképezésekhez tartozó mátrix nyoma 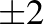 (lásd [3] 3. fejezetében).
(lásd [3] 3. fejezetében).
Ebben az írásban egy rövid ismertetést szeretnék adni egy olyan mintázatról, amely invariáns marad egy 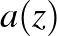 -vel jelölt loxodromikus és egy
-vel jelölt loxodromikus és egy 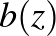 -vel jelölt parabolikus transzformáció által generált
-vel jelölt parabolikus transzformáció által generált 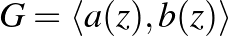 csoport hatására nézve. A
csoport hatására nézve. A 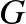 csoportban az összes lehetséges transzformációt meg lehet adni egy „szóval”, ábécéként az
csoportban az összes lehetséges transzformációt meg lehet adni egy „szóval”, ábécéként az 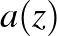 ,
, 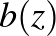 ,
,  ,
, 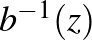 betűket használva. Ezt nevezzük az
betűket használva. Ezt nevezzük az 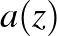 és
és 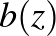 által generált Schottky-csoportnak, Friedrich Hermann Schottky (1851–1935) emlékére. Ha egy szóban az
által generált Schottky-csoportnak, Friedrich Hermann Schottky (1851–1935) emlékére. Ha egy szóban az 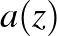 elem közvetlenül az inverze,
elem közvetlenül az inverze,  , mellett szerepel, akkor a szó leegyszerűsíthető az
, mellett szerepel, akkor a szó leegyszerűsíthető az 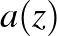 ,
,  pár elhagyásával, és hasonlóan a
pár elhagyásával, és hasonlóan a 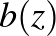 és a
és a 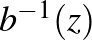 pár esetén. Így a
pár esetén. Így a 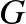 csoport szabad csoport (lásd [1] 23.3 Tétel, 92. o., és [3] 4. fejezetében).
csoport szabad csoport (lásd [1] 23.3 Tétel, 92. o., és [3] 4. fejezetében).

1.ábra
Az 1. ábrán látható fekete csipkemotívum a 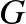 csoport „határpontjainak” a halmaza. Határpont alatt azokat a pontokat értjük, amelyeket megközelíthetünk, ha valamely más pontra alkalmazzuk
csoport „határpontjainak” a halmaza. Határpont alatt azokat a pontokat értjük, amelyeket megközelíthetünk, ha valamely más pontra alkalmazzuk 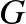 -beli leképezések egy végtelen sorozatát. Az euklideszi tapétázásoknak csak egy határpontja van. Escher Körhatár munkáinak határpontjai egy kört alkotnak (lásd [1] 50.o.). Az általunk vizsgált fenti mintázat határpontjainak halmaza végtelen sok körből és ezek torlódási pontjaiból áll (lásd 1. ábra).
-beli leképezések egy végtelen sorozatát. Az euklideszi tapétázásoknak csak egy határpontja van. Escher Körhatár munkáinak határpontjai egy kört alkotnak (lásd [1] 50.o.). Az általunk vizsgált fenti mintázat határpontjainak halmaza végtelen sok körből és ezek torlódási pontjaiból áll (lásd 1. ábra).

2. ábra
Az 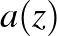 és
és 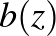 leképezések hatását a 2. ábra mutatja be, amelyen az 1. ábra egy véges részlete, egymást érintő körlapok láthatók. Az
leképezések hatását a 2. ábra mutatja be, amelyen az 1. ábra egy véges részlete, egymást érintő körlapok láthatók. Az 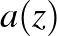 transzformáció az ibolya színű körlemezeket mozgatja balról jobbra, egyikről a következőre a piros nyilak irányába. Az
transzformáció az ibolya színű körlemezeket mozgatja balról jobbra, egyikről a következőre a piros nyilak irányába. Az 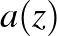 transzformáció loxodromikus, a pontokat egy végtelen dupla spirálon mozgatja a forrás fixpontból a nyelő fixpont irányába.
transzformáció loxodromikus, a pontokat egy végtelen dupla spirálon mozgatja a forrás fixpontból a nyelő fixpont irányába.
A 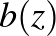 transzformáció, melynek hatására a mozgást a kék nyilak jelölik, a két világoskék körlemezt invariánsan hagyja. A
transzformáció, melynek hatására a mozgást a kék nyilak jelölik, a két világoskék körlemezt invariánsan hagyja. A 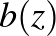 leképezés egyetlen fixpontja a két kék kör érintési pontja. Így
leképezés egyetlen fixpontja a két kék kör érintési pontja. Így 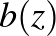 egy parabolikus leképezés, a pontokat a fixpontjából induló kör alakú pályákon mozgatja, azokon az óramutató járásával megegyező irányba haladva. A hozzá tartozó mátrix nyoma
egy parabolikus leképezés, a pontokat a fixpontjából induló kör alakú pályákon mozgatja, azokon az óramutató járásával megegyező irányba haladva. A hozzá tartozó mátrix nyoma 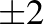 . Mátrixok nyomára vonatkozó azonosságok felhasználásával (lásd [3] 6. fejezetében) ez egy polinomiális összefüggést ad az
. Mátrixok nyomára vonatkozó azonosságok felhasználásával (lásd [3] 6. fejezetében) ez egy polinomiális összefüggést ad az 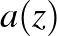 és a
és a 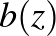 generátorokra.
generátorokra.
A 2. ábrán látható körháló komplementere négy fehér tartomány, ezeket a képen  jelöli. Az
jelöli. Az 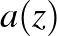 leképezés az
leképezés az  tartományt határoló köröket mozgatja az
tartományt határoló köröket mozgatja az  tartományt határoló körökbe, és hasonlóan mozgatja a
tartományt határoló körökbe, és hasonlóan mozgatja a 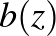 transzformáció a
transzformáció a  és a
és a  tartományokat határoló köröket. Az
tartományokat határoló köröket. Az 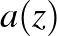 leképezés a
leképezés a  tartomány külsejét az
tartomány külsejét az  tartomány belsejére képezi le és hasonlóan a
tartomány belsejére képezi le és hasonlóan a 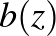 leképezés a
leképezés a  tartomány külsejét a
tartomány külsejét a  tartomány belsejére képezi le. Az
tartomány belsejére képezi le. Az 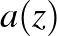 és a
és a 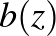 leképezéseket ismételve, egymásba ágyazott tartományok sorozatát kapjuk. Az egymásba ágyazott tartományok torlódási pontjai alkotják a Schottky-csoport határhalmazát.
leképezéseket ismételve, egymásba ágyazott tartományok sorozatát kapjuk. Az egymásba ágyazott tartományok torlódási pontjai alkotják a Schottky-csoport határhalmazát.

3.ábra
A 3. ábrán a körlemezek közötti transzformációkat jelképező nyilak zárt hurkait látjuk. Követve a nyilakat, melyek az 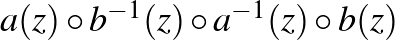 leképezések kompozícióját mutatják – először egy kék nyíl hat előre a nyíl irányába [
leképezések kompozícióját mutatják – először egy kék nyíl hat előre a nyíl irányába [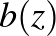 ], utána egy piros nyíl hat a nyíllal ellenkező irányba [
], utána egy piros nyíl hat a nyíllal ellenkező irányba [ ], aztán egy kék nyíl hat visszafelé [
], aztán egy kék nyíl hat visszafelé [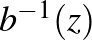 ], végül egy piros nyíl előre [
], végül egy piros nyíl előre [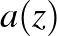 ] –, azt látjuk, hogy ez a transzformáció invariánsan hagyja a nagy külső „körlemezt”, azaz az
] –, azt látjuk, hogy ez a transzformáció invariánsan hagyja a nagy külső „körlemezt”, azaz az 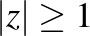 pontok halmazát, mely tartalmazza
pontok halmazát, mely tartalmazza 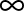 -t. Ezt
-t. Ezt 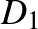 -gyel fogjuk jelölni. Ugyancsak invariánsan hagyja a bal oldali legnagyobb fehéreslila körlemezt. Ezt jelöljük
-gyel fogjuk jelölni. Ugyancsak invariánsan hagyja a bal oldali legnagyobb fehéreslila körlemezt. Ezt jelöljük 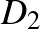 -vel. Ebből adódik, hogy az
-vel. Ebből adódik, hogy az 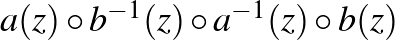 leképezés is parabolikus transzformáció. Így az
leképezés is parabolikus transzformáció. Így az 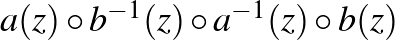 leképezéshez tartozó mátrix nyoma ismét
leképezéshez tartozó mátrix nyoma ismét 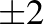 . Ha feltesszük, hogy
. Ha feltesszük, hogy 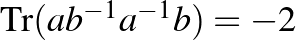 , akkor a mátrixok nyomára vonatkozó
, akkor a mátrixok nyomára vonatkozó
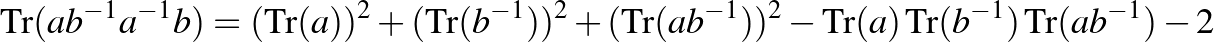
azonosság a
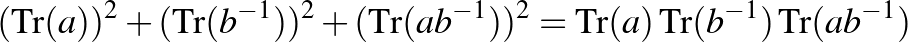
Markov-azonossággá egyszerűsödik, amely Andrej Andrejevics Markov (1856–1922) nevét őrzi. Így a 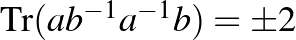 feltétel újabb polinomiális összefüggést ad az
feltétel újabb polinomiális összefüggést ad az 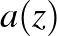 és a
és a 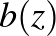 traszformációk között. A mátrixok nyomára vonatkozó azonosságok alkalmazása lehetővé teszi, hogy a
traszformációk között. A mátrixok nyomára vonatkozó azonosságok alkalmazása lehetővé teszi, hogy a 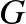 csoport minden „szavának” nyomát kifejezhessük a
csoport minden „szavának” nyomát kifejezhessük a 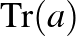 ,
, 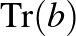 és a
és a  nyomok segítségével (lásd [3] 6. fejezet, 189–192. o.).
nyomok segítségével (lásd [3] 6. fejezet, 189–192. o.).
Továbbá ha 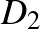 -nél kezdünk, és pontosan
-nél kezdünk, és pontosan 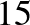 -ször alkalmazzuk egymás után az
-ször alkalmazzuk egymás után az 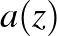 -t (a piros nyilakkal jelölt transzformációkat a nyilak irányában), akkor a jobb oldali szimmetrikusan elhelyezkedő legnagyobb fehéreslila körlemezhez érkezünk. És innen visszaugorhatunk
-t (a piros nyilakkal jelölt transzformációkat a nyilak irányában), akkor a jobb oldali szimmetrikusan elhelyezkedő legnagyobb fehéreslila körlemezhez érkezünk. És innen visszaugorhatunk 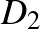 -re a
-re a 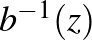 leképezés hatására (a kék nyíl által jelölt leképezést egyszer visszafelé, a nyíllal ellenkező irányban alkalmazva). Ugyanez a kompozíció invariánsan hagyja az
leképezés hatására (a kék nyíl által jelölt leképezést egyszer visszafelé, a nyíllal ellenkező irányban alkalmazva). Ugyanez a kompozíció invariánsan hagyja az 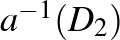 körlemezt, melyet éppen egy piros nyíl hatása képez
körlemezt, melyet éppen egy piros nyíl hatása képez 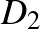 -re. (Az
-re. (Az 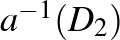 a
a 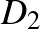 -t kívülről érintő kékesfehér körlemez.) Ezért
-t kívülről érintő kékesfehér körlemez.) Ezért 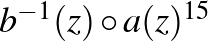 is parabolikus leképezés. Fixpontja a
is parabolikus leképezés. Fixpontja a 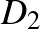 és az
és az 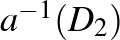 körlemezek érintési pontja. A
körlemezek érintési pontja. A 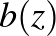 ,
, 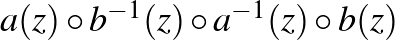 ,
, 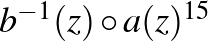 parabolikus leképezések által adott polinomiális feltételek (konjugálás erejéig) egyértelműen meghatározzák a mintázatot.
parabolikus leképezések által adott polinomiális feltételek (konjugálás erejéig) egyértelműen meghatározzák a mintázatot.
A körlemezek színezése a következőképpen történik: A 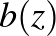 leképezés alkalmazása nem változtatja meg a színt. Az
leképezés alkalmazása nem változtatja meg a színt. Az 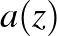 leképezést alkalmazva a körlemez színe a következő színre vált 15 szín ciklusában.
leképezést alkalmazva a körlemez színe a következő színre vált 15 szín ciklusában.
A 4. ábra a körlemezeknek a 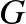 hatására vonatkozó két ekvivalenciaosztályát mutatja.
hatására vonatkozó két ekvivalenciaosztályát mutatja.

4.ábra
Ez kiterjeszti a körlemezek színezését az eredeti körhálóban. Minden körlemez invariáns a transzformációk egy részcsoportjának hatásával szemben. Például láttuk, hogy a 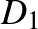 külső körlemez invariáns marad a
külső körlemez invariáns marad a 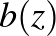 és az
és az 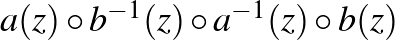 leképezések hatására. Ez a két szó generálja a
leképezések hatására. Ez a két szó generálja a 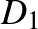 körlemez stabilizátor részcsoportját. Ebben a részcsoportban az összes szó olyan, hogy a bennük előforduló
körlemez stabilizátor részcsoportját. Ebben a részcsoportban az összes szó olyan, hogy a bennük előforduló 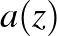 kifejezések kitevőinek az összege 0. Így a
kifejezések kitevőinek az összege 0. Így a 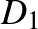 körlemez képének a színét a
körlemez képének a színét a 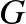 csoport szavainak hatására éppen a szavakban levő
csoport szavainak hatására éppen a szavakban levő 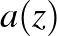 kifejezések kitevőinek az összege határozza meg.
kifejezések kitevőinek az összege határozza meg.
Hasonlóan a 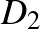 körlemez stabilizátora az
körlemez stabilizátora az 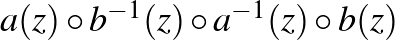 és a
és a 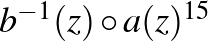 leképezések által van generálva. Ezen részcsoport minden szavában az
leképezések által van generálva. Ezen részcsoport minden szavában az 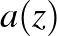 kitevőinek az összege
kitevőinek az összege 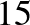 többszöröse. Ennélfogva a színezésünk konzisztens, ha
többszöröse. Ennélfogva a színezésünk konzisztens, ha 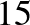 színt használunk.
színt használunk.
A teljes mintázaton keresztül a következő szabályt látjuk: Ha a 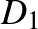 és a
és a 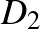 körlemez színét ugyanannak választjuk, akkor két érintő körlemez pontosan akkor tartozik különböző ekvivalenciaosztályhoz, ha ugyanaz a színük. Az ekvivalenciaosztályok a
körlemez színét ugyanannak választjuk, akkor két érintő körlemez pontosan akkor tartozik különböző ekvivalenciaosztályhoz, ha ugyanaz a színük. Az ekvivalenciaosztályok a 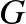 csoport egy 2 indexű részcsoportjához tartoznak.
csoport egy 2 indexű részcsoportjához tartoznak.
Ha kinagyítjuk a kép közepét, az 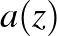 transzformáció fixpontjai mintha szemek lennének (lásd az 5. ábrát).
transzformáció fixpontjai mintha szemek lennének (lásd az 5. ábrát).

5.ábra
Az olyan csoportot, amelynek a határhalmaza kör, Fuchs-féle csoportnak nevezzük. A csoport elnevezése Immanuel Lazarus Fuchs (1833–1902) emlékét őrzi. Möbius-transzformációk egy csoportját, amelyek határhalmaza egy összefüggő hurok, kvázifuchs-féle csoportnak nevezzük. A 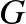 csoportot azért hívja David J.Wright „dupla csúcsú csoportnak” [4] cikkében, mert ez utal arra, hogy
csoportot azért hívja David J.Wright „dupla csúcsú csoportnak” [4] cikkében, mert ez utal arra, hogy 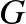 kétgenerátorú kvázifuchs-féle csoportok extrém „deformációja” (lásd [3] 6. és 9. fejezeteit).
kétgenerátorú kvázifuchs-féle csoportok extrém „deformációja” (lásd [3] 6. és 9. fejezeteit).
Hasonló tulajdonságú csoportokról és határhalmazukról Felix Cristian Klein (1849-1925) kutatásai úttörő jelentőséggel bírnak. Ez motiválta ennek az írásnak a címét. Munkássága során Klein fizikailag is vizualizált szimmetrikus mintázatokat. Azonban a határhalmaz ábrázolása olyan nehézségekkel szembesítette, amelyekről 1894-ben így írt (lásd [2]):
„A kérdés az, hogy milyen konfigurációt alkot a körök összessége és hogy mi lesz a határpontjaiknak a halmaza. Ezekre a kérdésekre nem nehéz választ adni tisztán logikai úton; de az érzékeltetésükben úgy látszik, meghiúsul a teljesség, ha megpróbáljuk az eredményt képként ábrázolni.”
További mintázatok elemzése és a számítógépes vizualizációjukhoz szükséges programok találhatók [3]-ban.
Ebben a cikkben az összes ábra szerzői joga David J. Wrightot illeti, aki David Mumforddal közösen írt „kleini” programukkal állította elő azokat, és újraközlésüket az Érintő számára engedélyezte.
Irodalomjegyzék
[1] T. K. Carne, Geometry and Groups, Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, https://www.dpmms.cam.ac.uk/~tkc/GeometryandGroups/GeometryandGroups.pdf
[2] F. Klein, Lectures on Mathematics, Amer. Math. Soc., 2000.
[3] D. Mumford, C. Series, and D. Wright, Indra's Pearls: The Vision of Felix Klein, Cambridge Univ. Press, 2002.
[4] D. Wright, Double Cusp Group, Notices of the AMS, 51, no. 11 (2004), 1332–1333.
https://www.ams.org/notices/200411/comm-wright.pdf
Debreceni Egyetem, Természettudományi és Technológiai Kar,
Matematikai Intézet, Debrecen
A munkát a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal (NKFI) K132951 és az EFOP-3.6.1-16-2016-00022 projekt támogatta. A második projektet az Európai Unió és az Európai Szociális Alap finanszírozza.









