A Monge–Kantorovics probléma
Az előző évtizedben két olyan matematikust is Fields-éremmel díjaztak (Cédric Villani 2010, Alessio Figalli 2018), akiknek munkájában az optimális transzport probléma jelentős szerepet játszott. A probléma születését Gaspard Monge 1781-ben publikált [4] művéhez, (egyik) újászületését pedig Leonyid Vitaljevics Kantorovics 1942-es [3] dolgozatához kötik.
Ebben a rövid írásban megpróbálom bemutatni a transzport probléma Monge- és Kantorovics-féle megfogalmazásait. A probléma történetéről, magáról a problémáról, és annak alkalmazásairól az érdeklődő olvasó többet is megtudhat Cédric Villani [7,8] és Filippo Santambrogio könyveiből [6].
1. A transzport probléma Monge-féle megfogalmazása
Gaspard Monge (1746–1818) hatalmas életművének csak egy apró szeletét képezik az optimális transzporttal kapcsolatos eredmények. Őt tekintik többek közt az ábrázoló geometria megteremtőjének, a differenciálgeometria egyik atyjának, de részt vett a méterrendszer kidolgozásában, sőt végzett fizikai és kémiai kutatásokat is. Tudományos eredményeit a hadviselésben is kamatoztatta, őt bízták meg annak megtervezésével, hogy hogyan érdemes ágyúkat elhelyezni egy erődítményben, később könyvet is írt az ágyúkészítés tudományáról [5]. Ide kívánkozik egy megjegyzés a Monge–Kantorovics probléma másik érintettjéről. Leningrád ostromakor a befagyott Ladoga-tó kiemelt stratégiai fontosságú volt a Vörös Hadsereg számára, ugyanis azon keresztül vezetett az étel és muníció szállítására alkalmas út. Kantorovics feladata volt, hogy kiszámolja a kocsik optimális távolságát és terhelhetőségét a jég vastagsága és a hőmérséklet függvényében [2].
Visszatérve Monge tudományos munkásságára: az optimális transzport probléma motivációját is egy meglehetősen egyszerű (illetve egyszerűnek hangzó) kérdés szolgáltatta. Nagyon elnagyoltan megfogalmazva: ha adott egy halom föld, és egy azzal megegyező térfogatú gödör, akkor hogyan tervezük meg a gödör feltöltését, ha azt a lehető legkevesebb munkával szeretnénk kivitelezni?

A problémát Monge geometriai módszerekkel próbálta megfogni: azt vizsgálta, hogy a tömeget milyen pályák (görbék) mentén kell mozgatni. Mielőtt kísérletet tennénk a feladat formalizálására, nézzünk meg egy hasonló, de ránézésre legalábbis jóval egyszerűbb, kérdést. Tegyük fel, hogy van egy teljes páros gráfunk ![]() elemű csúcsosztályokkal (jelölje ezeket
elemű csúcsosztályokkal (jelölje ezeket ![]() és
és ![]() ). Tegyük fel továbbá, hogy adott egy
). Tegyük fel továbbá, hogy adott egy ![]() költségfüggvény. Gondoljunk erre úgy, hogy
költségfüggvény. Gondoljunk erre úgy, hogy ![]() nem más, mint az
nem más, mint az ![]() pont
pont ![]() -vel való párosításának költsége. Kérdés: az összes teljes párosítás közül melyik a minimális összköltségű? Világos, hogy minden teljes párosítás megadható egy
-vel való párosításának költsége. Kérdés: az összes teljes párosítás közül melyik a minimális összköltségű? Világos, hogy minden teljes párosítás megadható egy ![]() bijekcióval, a
bijekcióval, a ![]() párosítás összköltsége pedig nem más, mint
párosítás összköltsége pedig nem más, mint ![]() . Tehát keressük azt a
. Tehát keressük azt a ![]() leképezést, ami ezt az összeget minimalizálja. Létezik ilyen párosítás, hiszen egy véges számhalmaz legkisebb elemét keressük.
leképezést, ami ezt az összeget minimalizálja. Létezik ilyen párosítás, hiszen egy véges számhalmaz legkisebb elemét keressük.
A párosítási feladat semmivel sem lesz bonyolultabb, ha átfogalmazzuk szállítási feladattá: minden ![]() raktárnak van
raktárnak van ![]() súlyú kiszállítandó rakománya, mindegyik
súlyú kiszállítandó rakománya, mindegyik ![]() bolt éppen
bolt éppen ![]() súlyú rakományra adott le rendelést, a
súlyú rakományra adott le rendelést, a ![]() mennyiség pedig az egyszerűség kedvért legyen most az
mennyiség pedig az egyszerűség kedvért legyen most az ![]() raktár és
raktár és ![]() bolt távolsága. Ekkor a szállítás során elvégzett munka nem más, mint
bolt távolsága. Ekkor a szállítás során elvégzett munka nem más, mint ![]() . Az azonban komoly nehezítés lenne, ha az egységnyi súlyt nem egyforma darabokra vágnánk szét mindkét oldalon, hanem különböző
. Az azonban komoly nehezítés lenne, ha az egységnyi súlyt nem egyforma darabokra vágnánk szét mindkét oldalon, hanem különböző ![]() és
és ![]() darabokra. Egy
darabokra. Egy ![]() bijekció ebben az esetben csak akkor adna meg jó szállítást, ha a
bijekció ebben az esetben csak akkor adna meg jó szállítást, ha a ![]() egyenlőség maga után vonná, hogy
egyenlőség maga után vonná, hogy ![]() , vagy másképpen felírva
, vagy másképpen felírva
| (1) |
Egy ilyen ![]() szállítás költsége az előzőek mintájára
szállítás költsége az előzőek mintájára
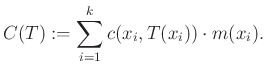 |
(2) |
Mivel véges sok ponttal dolgoztunk, és így csak véges sok jó ![]() leképezés lehet, ezért az
leképezés lehet, ezért az
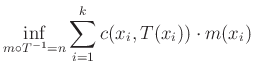 |
(3) |
infimum valójában egy minimum. Tehát ha van legalább egy jó szállítás, akkor van optimális is. Vegyük észre, hogy amit itt látunk, az Monge problémájának egy diszkretizált változata: a földkupac és a betemetendő gödör helyett két diszkrét tömegeloszlás van, és keressük azt a ![]() leképezést, ami az egyiket minimális költséggel transzportálja át a másikba. Már ezen a diszkrét eseten jól látszik két probléma
leképezést, ami az egyiket minimális költséggel transzportálja át a másikba. Már ezen a diszkrét eseten jól látszik két probléma
- a) Nem feltétlenül van megoldása a Monge által kitűzött problémának, hiszen az alábbi ábrán
-
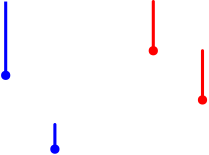
az (1) feltétel egyetlen olyan leképezésre sem teljesülhet, ami a kék pontokat a piros pontokra képezi.
b) Ha van megoldás, nem feltétlenül egyértelmű.
-
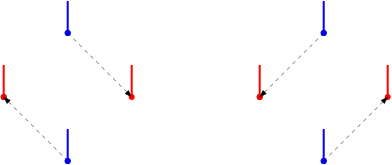
Mivel a piros és kék pontok közötti távolságok egyenlőek, és a mozgatni kívánt súlyok egyenletesen vannak szétosztva, ezért a szaggatott nyilak mentén két különböző optimális transzportot látunk.
Nézzük meg, hogy hogyan lehet felírni az általános problémát. A metrikus tér, amiben dolgozunk, az ![]() -dimenziós euklidészi tér a szokásos távolsággal, a költségfüggvény pedig egy nemnegatív értékű folytonos
-dimenziós euklidészi tér a szokásos távolsággal, a költségfüggvény pedig egy nemnegatív értékű folytonos ![]() függvény. A kupacnak és a gödörnek pedig egy-egy Borel valószínűségi mérték felel meg. (Legyen a kupac eloszlásának megfelelő mérték
függvény. A kupacnak és a gödörnek pedig egy-egy Borel valószínűségi mérték felel meg. (Legyen a kupac eloszlásának megfelelő mérték ![]() , a gödöré
, a gödöré ![]() .) A transzport leképezésre vonatkozó (1) feltétel megfelelője az általános esetben az, hogy
.) A transzport leképezésre vonatkozó (1) feltétel megfelelője az általános esetben az, hogy ![]() egy olyan mérhető függvény kell legyen, amelyre
egy olyan mérhető függvény kell legyen, amelyre ![]() teljesül minden
teljesül minden ![]() Borel-halmaz esetén.
Borel-halmaz esetén.
Ilyenkor azt mondjuk, hogy a ![]() mérték a
mérték a ![]() -nek
-nek ![]() -szerinti előretoltja, jelölésben:
-szerinti előretoltja, jelölésben: ![]() .
.

Ezek után már könnyű látni, hogy a (2) formula általános megfelelője nem más, mint
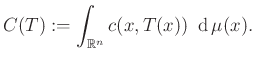
Szemben a fenti (3) diszkrét esettel itt semmilyen egyszerű gondolatmenet nem garantálja, hogy ha egyáltalán van transzport leképezés (azaz a ![]() funkcionál értelmezési tartománya nem üres), akkor az
funkcionál értelmezési tartománya nem üres), akkor az
infimum valójában egy minimum, tehát hogy a ![]() funkcionál felveszi a minimumát. Olyannyira nem garantálja ezt semmilyen egyszerű gondolatmenet, hogy több mint 200 évet kellett várni a következő szép eredményre: ha a
funkcionál felveszi a minimumát. Olyannyira nem garantálja ezt semmilyen egyszerű gondolatmenet, hogy több mint 200 évet kellett várni a következő szép eredményre: ha a ![]() mérték abszolút folytonos az
mérték abszolút folytonos az ![]() -dimenziós Lebesgue-mértékre vonatkozóan, akkor létezik optimális transzport leképezés [1].
-dimenziós Lebesgue-mértékre vonatkozóan, akkor létezik optimális transzport leképezés [1].
2. A transzport probléma Kantorovics-féle megfogalmazása
A Monge-probléma egyik nehézsége a „kompaktság hiányában” rejlik, azaz hogy ha adott is a ![]() -t
-t ![]() -be mozgató transzport leképezéseknek egy
-be mozgató transzport leképezéseknek egy ![]() sorozata, nem ismert olyan topológia, amely szerint
sorozata, nem ismert olyan topológia, amely szerint ![]() -ből kiválasztható konvergens részsorozat. Több mint 150 évvel később Leonyid Kantorovicsnak, a lineáris programozás egyik szülőatyjának sikerült áthidalnia ezt a problémát. A felfedezés fontosságát és hasznosságát jól mutatja, hogy 1975-ben Tjalling Koopmansszal megosztva közgazdasági Nobel-díjjal tüntették ki az erőforrások optimális elosztásának elméletéhez való hozzájárulásáért.
-ből kiválasztható konvergens részsorozat. Több mint 150 évvel később Leonyid Kantorovicsnak, a lineáris programozás egyik szülőatyjának sikerült áthidalnia ezt a problémát. A felfedezés fontosságát és hasznosságát jól mutatja, hogy 1975-ben Tjalling Koopmansszal megosztva közgazdasági Nobel-díjjal tüntették ki az erőforrások optimális elosztásának elméletéhez való hozzájárulásáért.
A transzport probléma új, relaxált megfogalmazásánál kibővítette a ![]() funkcionál értelmezési tartományát, és nem csak transzport leképezéseket, hanem úgynevezett transzport terveket is megengedett. Nézzünk egy olyan példát, amit a Monge-féle megfogalmazás szerint nem lehet megoldani.
funkcionál értelmezési tartományát, és nem csak transzport leképezéseket, hanem úgynevezett transzport terveket is megengedett. Nézzünk egy olyan példát, amit a Monge-féle megfogalmazás szerint nem lehet megoldani.
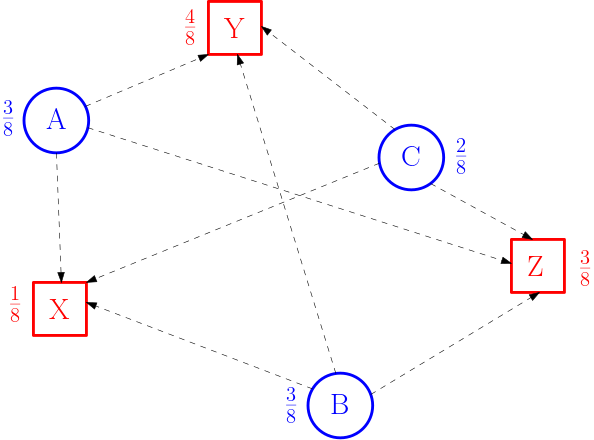
Világos, hogy nincs olyan ![]() leképezés, amelyik teljesíti az (1) feltételt. Ha meg volna engedve, hogy a kék körökön lévő súlyokat feldaraboljuk, és azokat különböző piros négyzetekbe szállítsuk, az jelentősen megkönnyíteni a dolgunkat. Az alábbi táblázat egy ilyen felosztást mutat.
leképezés, amelyik teljesíti az (1) feltételt. Ha meg volna engedve, hogy a kék körökön lévő súlyokat feldaraboljuk, és azokat különböző piros négyzetekbe szállítsuk, az jelentősen megkönnyíteni a dolgunkat. Az alábbi táblázat egy ilyen felosztást mutat.
| X | Y | Z | |
| A | |
|
|
| B | 0 | |
0 |
| C | 0 | 0 | |
Ha csak egy sort nézünk, azt látjuk, hogy az adott kék körön lévő súlyt hogyan daraboljuk fel, és melyik darabot melyik piros négyzetbe küldjük. Ha csak egy oszlopot nézünk, azt látjuk, hogy az adott piros négyzetbe melyik kék körből mennyi súly érkezik. Adott ![]() költségfüggvény mellett ennek a transzport tervnek a költsége
költségfüggvény mellett ennek a transzport tervnek a költsége
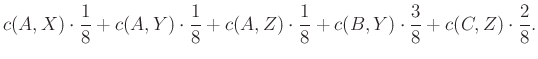
A táblázatra kicsit másképp ránézve egy valószínűségi eloszlást látunk az ![]() halmazon, amelynek egyik peremeloszlása épp a kék eloszlás, a másik pedig a piros eloszlás. Általában persze ilyen eloszlásból nem csak egy van, a fenti szállítási feladatot is sokféleképp meg lehet oldani. A feladat a legkisebb költségű ilyan transzport terv megtalálása.
halmazon, amelynek egyik peremeloszlása épp a kék eloszlás, a másik pedig a piros eloszlás. Általában persze ilyen eloszlásból nem csak egy van, a fenti szállítási feladatot is sokféleképp meg lehet oldani. A feladat a legkisebb költségű ilyan transzport terv megtalálása.
Nézzük hogyan írható át a Kantorovics-féle megfogalmazás az általános esetre. Legyen ![]() és
és ![]() két Borel valószínűségi mérték
két Borel valószínűségi mérték ![]() -en, az ezen mértékekhez tartozó transzport tervek halmazát jelölje
-en, az ezen mértékekhez tartozó transzport tervek halmazát jelölje ![]() . Ezek tehát azok a
. Ezek tehát azok a ![]() mértékek a szorzat téren, amelyeknek marginálisai
mértékek a szorzat téren, amelyeknek marginálisai ![]() és
és ![]()
Fontos megjegyezni, hogy a ![]() halmaz sosem üres, hiszen
halmaz sosem üres, hiszen ![]() és
és ![]() szorzatmértéke benne van. Egy
szorzatmértéke benne van. Egy ![]() transzport terv költsége
transzport terv költsége
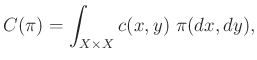
a feladatunk pedig a ![]() funkcionál minimalizálása. Azaz keressük azt a
funkcionál minimalizálása. Azaz keressük azt a ![]() transzport leképezést, amelyre
transzport leképezést, amelyre
Szemben a Monge-féle megfogalmazással, ez a minimalizálási feladat mindig megoldható. (Legalábbis abban a speciális esetben, amit itt tárgyalunk, tehát amikor az alaptér ![]() , a költségfüggvény pedig egy folytonos nemnegatív függvény.) Ennek az az oka, hogy a transzport tervek tere sokkal jobb tulajdonságokkal rendelkezik, mint a transzport leképezéseké.
, a költségfüggvény pedig egy folytonos nemnegatív függvény.) Ennek az az oka, hogy a transzport tervek tere sokkal jobb tulajdonságokkal rendelkezik, mint a transzport leképezéseké.
Nagyon vázlatosan a következőről van szó: az egyszerűség kedvéért tegyük fel, hogy van legalább egy ![]() , amelyre
, amelyre ![]() nem végtelen. Ekkor az
nem végtelen. Ekkor az
infimum egy nemnegatív valós szám, így van olyan ![]() -ben haladó
-ben haladó ![]() sorozat, amelyre
sorozat, amelyre ![]() Azt kell megmutatunk, hogy maga a
Azt kell megmutatunk, hogy maga a ![]() sorozat valamilyen értelemben konvergál egy
sorozat valamilyen értelemben konvergál egy ![]() -beli elemhez.
-beli elemhez.
Ehhez szükségünk van a következő fogalomra: valószínűségi mértékek egy ![]() mértékcsaládját feszesnek nevezzük, ha minden
mértékcsaládját feszesnek nevezzük, ha minden ![]() számhoz van olyan
számhoz van olyan ![]() kompakt halmaz, hogy minden
kompakt halmaz, hogy minden ![]() esetén
esetén ![]() .
.
Megmutatjuk, hogy a ![]() sorozat (mint mértékcsalád) feszes. Tudjuk, hogy a
sorozat (mint mértékcsalád) feszes. Tudjuk, hogy a ![]() mértékek marginálisai
mértékek marginálisai ![]() és
és ![]() . Azt könnyű belátni, hogy minden
. Azt könnyű belátni, hogy minden ![]() -hoz léteznek olyan
-hoz léteznek olyan ![]() és
és ![]() kompakt halmazok, amelyekre
kompakt halmazok, amelyekre ![]() és
és ![]() . Az ezekből képzett
. Az ezekből képzett ![]() kompakt halmazok pedig garantálják
kompakt halmazok pedig garantálják ![]() feszességét. Ezen a ponton használhatjuk Prokhorov híres tételét, nevezetesen hogy a feszesség miatt a sorozatból kiválasztható gyengén konvergens részsorozat. (Emlékeztetünk, hogy
feszességét. Ezen a ponton használhatjuk Prokhorov híres tételét, nevezetesen hogy a feszesség miatt a sorozatból kiválasztható gyengén konvergens részsorozat. (Emlékeztetünk, hogy ![]() gyengén konvergál
gyengén konvergál ![]() -hoz, ha minden folytonos korlátos függvény
-hoz, ha minden folytonos korlátos függvény ![]() szerinti integráljaiból kapott sorozat konvergál a függvény
szerinti integráljaiból kapott sorozat konvergál a függvény ![]() szerinti integráljához.) Jelölje a konvergens részsorozat limeszét
szerinti integráljához.) Jelölje a konvergens részsorozat limeszét ![]() . Könnyen igazolható, hogy
. Könnyen igazolható, hogy ![]() . A bizonyítás befejezéséhez elég megmutatni, hogy
. A bizonyítás befejezéséhez elég megmutatni, hogy
Ha a ![]() költségfüggvény korlátos és folytonos, akkor ez a gyenge konvergencia definíciójából és a
költségfüggvény korlátos és folytonos, akkor ez a gyenge konvergencia definíciójából és a ![]() választásából azonnal következik, ha nem, akkor egy standard határátmenetet használó okoskodással vissza lehet vezetni a problémát a folytonos korlátos esetre.
választásából azonnal következik, ha nem, akkor egy standard határátmenetet használó okoskodással vissza lehet vezetni a problémát a folytonos korlátos esetre.
Ezzel vázlatosan megmutattuk, hogy az általunk vizsgált esetben a Kantorovich-féle probléma megoldható. A fenti okoskodás lépései akkor is működtek volna, ha ![]() helyett egy szeparábilis teljes metrikus teret tekintettünk volna, a
helyett egy szeparábilis teljes metrikus teret tekintettünk volna, a ![]() költségfüggvényről pedig alulról félig folytonosságot tettünk volna fel.
költségfüggvényről pedig alulról félig folytonosságot tettünk volna fel.
A cikket egy egyszerű észrevétellel zárjuk, amely kapcsolatot teremt a probléma két megfogalmazása között. Tegyük fel először, hogy ![]() egy transzport leképezés, azaz
egy transzport leképezés, azaz ![]() , és tekintsük az
, és tekintsük az  hozzárendeléssel megadott
hozzárendeléssel megadott  függvényt.
függvényt.
Ekkor ![]() és
és ![]() , és az
, és az ![]() mérték a
mérték a ![]() grafikonjára van koncentrálva. Megfordítva, ha
grafikonjára van koncentrálva. Megfordítva, ha ![]() egy olyan mérték, amely egy függvény grafikonjára van koncentrálva, akkor van olyan
egy olyan mérték, amely egy függvény grafikonjára van koncentrálva, akkor van olyan ![]() transzport leképezés, amelyre
transzport leképezés, amelyre ![]() .
.
A cikk az ITM és az NKFIH ÚNKP-19-4-BGE-1 és PD128374 kódszámú projektjeinek, valamint az MTA Bolyai János Kutatási Ösztöndíjának támogatásával készült.
Irodalomjegyzék
- [1] L. C. Evans, W. Gangbo, Differential Equations Methods for the Monge–Kantorovich Mass Transfer Problem, Memoirs of the American Mathematical Society No. 137, 1999.
- [2] B. Gustafsson, Scientific Computing: A Historical Perspective, Texts in Computational Science and Engineering, Springer, 2018.
- [3] L. Kantorovich, On translation of mass, C.R. Doklady. Acad Sci USSR. 1942;37 199–201.
- [4] G. Monge, Mémoire sur la théorie des déblais et des remblais. De l’Imprimerie Royale; 1781.
- [5] G. Monge, Description de l'art de fabriquer des canons, Éditeur: Imprimerie du comité de salut publique, Paris, Publication: an 2 de la république francaise (1793–1794).
- [6] F. Santambrogio, Optimal transport for applied mathematicians. Birkäuser Springer, Basel, 2015.
- [7] C. Villani, Topics in Optimal Transportation. American Mathematical Society, 2003.
- [8] C. Villani, Optimal Transport: Old and New, Volume 338. Springer Verlag.
Titkos Tamás
Rényi Alfréd Matematikai Kutatóintézet
és Budapesti Gazdasági Egyetem









