A π az idők viharában
Már a régi görögök is...
A ![]() -ről már a régi görögök is tudtak: bármely két kör hasonló, ezért bármely kör kerületének és átmérőjének aránya ugyanannyi.
-ről már a régi görögök is tudtak: bármely két kör hasonló, ezért bármely kör kerületének és átmérőjének aránya ugyanannyi.
Arkhimédész beírt és körülírt szabályos sokszögekkel próbálta megközelíteni az egységnyi átmérőjű kör kerületét. Szabályos hatszögekből kiindulva és lépésenként kétszerezve a sokszögek csúcsai számát eljuthatunk a körülírt és a beírt szabályos 96-szög kerületéhez, amelyből 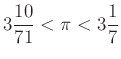 .
.
A babilóniaiak 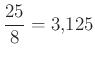 -nek, a Rhind-papirusz tanúsága szerint pedig az egyiptomiak
-nek, a Rhind-papirusz tanúsága szerint pedig az egyiptomiak 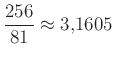 -nek vették a
-nek vették a ![]() -t.
-t.
Ám a ![]() , bár görög betű, nem az ógörögöktől, de még csak nem is az ókorban kapta a nevét.
, bár görög betű, nem az ógörögöktől, de még csak nem is az ókorban kapta a nevét.
Írásos feljegyzések szerint William Jones walesi matematikus használta először a ![]() -t a kör kerületének (periféria) és átmérőjének arányára egy 1706-ban megjelent munkájában. Ezt a jelölést vette át Leonhard Euler svájci matematikus az 1730-as években, és innen terjedt el a világon.
-t a kör kerületének (periféria) és átmérőjének arányára egy 1706-ban megjelent munkájában. Ezt a jelölést vette át Leonhard Euler svájci matematikus az 1730-as években, és innen terjedt el a világon.
A π irracionális, sőt!
Sokáig kérdés volt, hogy egyáltalán racionális szám-e a ![]() .
.
Akkoriban két egész szám hányadosaként felírva kaptak alkalmas közelítéseket, például 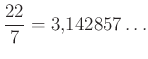 ,
, 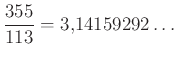 , de – bárhogy kerestek – nem találtak megfelelő racionális alakot rá.
, de – bárhogy kerestek – nem találtak megfelelő racionális alakot rá.
Keresték a ![]() lánctört alakját is. Amennyiben egy tört nagyobb 1-nél, akkor vegyes tört alakban felírva kisebb számokkal tudjuk felírni. Például
lánctört alakját is. Amennyiben egy tört nagyobb 1-nél, akkor vegyes tört alakban felírva kisebb számokkal tudjuk felírni. Például 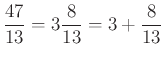 . Ugyanakkor a
. Ugyanakkor a ![]() úgy írható, hogy
úgy írható, hogy ![]() , így a nevezőben szereplő törtről ismét leválasztható az egész része:
, így a nevezőben szereplő törtről ismét leválasztható az egész része: 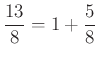 , azaz
, azaz 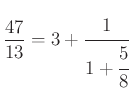 és így tovább, végül ezt a lánctörtet kapjuk:
és így tovább, végül ezt a lánctörtet kapjuk:
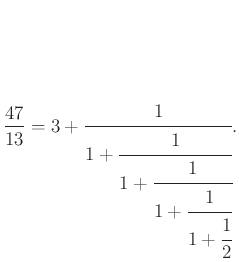
A lánctörtet szokás úgy jelölni, hogy szögletes zárójelek között felsoroljuk az egész részeket, az első után pontosvesszőt teszünk, a többi után vesszőt. Esetünkben: ![$ \frac{47}{13}=[3;1,1,1,1,2]$](/images/stories/latex/pivegleges/img13.png) . A számelméletben jártasabbak felismerhetik az eljárásban az euklideszi algoritmust. Minden racionális szám lánctört alakja véges, és minden véges lánctört racionális szám.
. A számelméletben jártasabbak felismerhetik az eljárásban az euklideszi algoritmust. Minden racionális szám lánctört alakja véges, és minden véges lánctört racionális szám.
Az irracionális számok lánctört alakja ugyan végtelen, de olykor „olvashatóbb”, megjegyezhetőbb, mint a tizedes tört alakja, például: ![]() .
.
A ![]() lánctört alakja azonban nem ilyen szabályos:
lánctört alakja azonban nem ilyen szabályos: ![]() . A korábban említett
. A korábban említett ![]() és
és felírások a
![]() lánctörtfelírásából kaphatók:
lánctörtfelírásából kaphatók:
![$\displaystyle [3;7]=3+\frac{1}{7}=\frac{22}{7},\qquad [3;7,15,1]=3+\cfrac{1}{7+\cfrac{1}{15+\cfrac{1}{1}}}
$](/images/stories/latex/pivegleges/img18.png)
A ![]() azonban nem racionális. Irracionalitását 1761-ben – alig 260 éve(!) – Johann Heinrich Lambert bizonyította be először. (Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques. Histoire de l'Académie Royale des Sciences et des Belles-Lettres de Berlin (megjelent 1768-ban), 17, 265–322.)
azonban nem racionális. Irracionalitását 1761-ben – alig 260 éve(!) – Johann Heinrich Lambert bizonyította be először. (Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques. Histoire de l'Académie Royale des Sciences et des Belles-Lettres de Berlin (megjelent 1768-ban), 17, 265–322.)
De nem csak irracionális a ![]() , hanem még transzcendens is. Ez azt jelenti, hogy nincs olyan legalább elsőfokú egész együtthatós polinom, amelynek gyöke lenne. (Szemben például a
, hanem még transzcendens is. Ez azt jelenti, hogy nincs olyan legalább elsőfokú egész együtthatós polinom, amelynek gyöke lenne. (Szemben például a ![]() -vel, amely ugyan irracionális, de nem transzcendens, mert gyöke az
-vel, amely ugyan irracionális, de nem transzcendens, mert gyöke az ![]() egész együtthatós polinomnak.) A
egész együtthatós polinomnak.) A ![]() transzcendenciájának bizonyításával többen is próbálkoztak (Hermite, Weierstrass, Euler), akiknek az eredményeit felhasználva a végső lépést Ferdinand von Lindemann tette meg 1882-ben, azaz nem egészen 140 éve. A tétel Lindemann–Weierstrass néven vált ismertté.
transzcendenciájának bizonyításával többen is próbálkoztak (Hermite, Weierstrass, Euler), akiknek az eredményeit felhasználva a végső lépést Ferdinand von Lindemann tette meg 1882-ben, azaz nem egészen 140 éve. A tétel Lindemann–Weierstrass néven vált ismertté.
A π nem szerkeszthető, a kör nem négyszögesíthető.
Az, hogy a kör nem négyszögesíthető, azt jelenti, hogy ha adott egy 1 átmérőjű kör (és más nem), akkor euklideszi módon nem szerkeszthetünk olyan négyzetet, amelynek ugyanakkora a területe, mint ennek a körnek. Ez ugyanazt jelenti, mint hogy ha adott egy egység hosszú szakasz (és más nem), akkor nem tudunk ![]() hosszúságú szakaszt szerkeszteni.
hosszúságú szakaszt szerkeszteni.
A koordinátasíkon a ![]() és az
és az ![]() pontokból kiindulva (más pontot nem ismerve) nem minden pontot tudunk megszerkeszteni (körző és vonalzó segítségével, a szokásos lépéseket véges sokszor végezve). Az egység hosszúságú szakasz egész számszorosait szakaszmásolással meg tudjuk szerkeszteni, sőt, párhuzamos szelők tétele alapján racionális hosszúságokat is meg tudunk szerkeszteni. Egyenes és egyenes metszéspontja a meghatározó pontok koordinátáiból összeadás, kivonás, szorzás és osztás segítségével egyszerűen megkapható, de kör és egyenes, illetve két kör metszéspontja olyan pontokat eredményezhet, amelyek koordinátáinak felírásához (az alakzatokat meghatározó pontok koordinátáiból kiindulva) négyzetgyökvonás szükséges.
pontokból kiindulva (más pontot nem ismerve) nem minden pontot tudunk megszerkeszteni (körző és vonalzó segítségével, a szokásos lépéseket véges sokszor végezve). Az egység hosszúságú szakasz egész számszorosait szakaszmásolással meg tudjuk szerkeszteni, sőt, párhuzamos szelők tétele alapján racionális hosszúságokat is meg tudunk szerkeszteni. Egyenes és egyenes metszéspontja a meghatározó pontok koordinátáiból összeadás, kivonás, szorzás és osztás segítségével egyszerűen megkapható, de kör és egyenes, illetve két kör metszéspontja olyan pontokat eredményezhet, amelyek koordinátáinak felírásához (az alakzatokat meghatározó pontok koordinátáiból kiindulva) négyzetgyökvonás szükséges.
Ahhoz tehát, hogy egy pontot meg tudjunk szerkeszteni a két kiinduló pontból, az kell, hogy a koordintátáit egész számokból kiindulva véges sok összeadás, kivonás, szorzás, osztás és négyzetgyökvonás segítségével fel lehessen írni. Így már az ![]() polinom valós gyöke, a
polinom valós gyöke, a ![]() sem szerkeszthető – pedig nem transzcendens –, mert a 2 köbgyöke nem írható fel négyzetgyök segítségével. Ám mivel a
sem szerkeszthető – pedig nem transzcendens –, mert a 2 köbgyöke nem írható fel négyzetgyök segítségével. Ám mivel a ![]() transzcendens, nemcsak hogy négyzetgyökök, de semmilyen gyökök segítségével sem írható fel, ezért az sem szerkeszthető a kiinduló két pontból, így nem szerkeszthető olyan négyzet sem, amelynek a területe
transzcendens, nemcsak hogy négyzetgyökök, de semmilyen gyökök segítségével sem írható fel, ezért az sem szerkeszthető a kiinduló két pontból, így nem szerkeszthető olyan négyzet sem, amelynek a területe ![]() .
.
Mindezek ellenére 1894-ben bizonyos Edward J. Goodwin orvos és amatőr matematikakutató cikket írt a kör négyszögesítéséről – és így a ![]() szerkeszthetőségről. A cikket a neves American Mathematical Monthly folyóirat közölte, igaz, azzal a nem túl hízelgő kitétellel, hogy a megjelentetés „a szerző kérésére” történt.
szerkeszthetőségről. A cikket a neves American Mathematical Monthly folyóirat közölte, igaz, azzal a nem túl hízelgő kitétellel, hogy a megjelentetés „a szerző kérésére” történt.
Ennek nyomán Goodwin kezdeményezte, hogy Indiana Állam egyik képviselője, Taylor I. Record terjesszen be egy törvényjavaslatot „Törvényjavaslat egy új matematikai igazság bevezetésére, felajánlva az oktatáshoz való hozzájárulásként, Indiana Állam kizárólagos használatára mindenféle ellenszolgáltatás vagy bármilyen fizetség nélkül, amennyiben azt az 1897-es törvénykezés elfogadja és befogadja” címmel. (Forrás: az eredeti újság, amely beszámol a hírről: 11. oldal, harmadik hasáb alsó harmadában: THE MATHEMATICAL BILL második bekezdés, amely szerint Record képviselő beterjesztett egy javaslatot egy, a kör négyszögesítésére vonatkozó matematikai képlet legalizálására.) A törvényjavaslat tárgyalását némi derültséggel fogadták a képviselők, akiket addigra Clarence A. Waldo professzor felkészített, elmagyarázva nekik a törvényben foglaltak banalitását. ☺
De mégse ítélkezzünk Goodwin felett, nem ő az egyetlen a matematiktörténelemben, aki nagyot tévedett.
A π mindentudó(?)
Patrick Ingram, a torontói York University matematikusa állítja: „úgy hisszük – bár nincs rá bizonyítékunk –, hogy a ![]() végeláthatatlan 0-tól 9-ig terjedő számjegyekből álló számsorozatában minden lehetséges számkombináció előfordul, és nem is csak egyszer, de újra és újra, végtelen sokszor.” (Ez a tulajdonság az úgynevezett normalitásnak a következménye. A
végeláthatatlan 0-tól 9-ig terjedő számjegyekből álló számsorozatában minden lehetséges számkombináció előfordul, és nem is csak egyszer, de újra és újra, végtelen sokszor.” (Ez a tulajdonság az úgynevezett normalitásnak a következménye. A ![]() normalitását ez idáig nem sikerült sem bebizonyítani, sem cáfolni.)
normalitását ez idáig nem sikerült sem bebizonyítani, sem cáfolni.)
David Andersen honlapján kipróbálhatjuk, hogy egy általunk megadott többjegyű szám megtalálható-e a ![]() első kétmilliárd számjegyének sorozatában.
első kétmilliárd számjegyének sorozatában.
Fried Katalin
ELTE TTK Matematikai Intézet Matematikatanítási és Módszertani Központ
A ![]() -ről készült kép szerzője Gordon Johson, https://pixabay.com/hu/vectors/pi-matematika-math-sz%C3%A1mok-3-14-3166192/.
-ről készült kép szerzője Gordon Johson, https://pixabay.com/hu/vectors/pi-matematika-math-sz%C3%A1mok-3-14-3166192/.









