A cikksorozat első részében vázlatosan ismertettük a (csak ohmos ellenállásokat tartalmazó) ![]() -port hálózat fogalmát, és megmutattuk, hogy hogyan modellezhető lineáris algebrai módszerekkel a hálózat rövidre zárása. Bevezettük a négyzetes mátrixok lineáris alterekre vonatkozó
-port hálózat fogalmát, és megmutattuk, hogy hogyan modellezhető lineáris algebrai módszerekkel a hálózat rövidre zárása. Bevezettük a négyzetes mátrixok lineáris alterekre vonatkozó ![]() zárlatát, mint az
zárlatát, mint az
halmaznak a ![]() részbenrendezésre nézve legnagyobb elemét. Emlékeztetünk arra, hogy a
részbenrendezésre nézve legnagyobb elemét. Emlékeztetünk arra, hogy a ![]() mátrix kvadratikus alakjára formulánk is volt
mátrix kvadratikus alakjára formulánk is volt
és hogy ![]() alatt a kvadratikus alakok pontonkénti rendezését értjük, azaz
alatt a kvadratikus alakok pontonkénti rendezését értjük, azaz ![]() , ha minden
, ha minden ![]() -ra
-ra ![]() . Ebben a részben azt az egyszerűnek hangzó, de igen bonyolult kérdést vesszük górcső alá, hogy a
. Ebben a részben azt az egyszerűnek hangzó, de igen bonyolult kérdést vesszük górcső alá, hogy a ![]() részbenrendezésre nézve mikor van két pozitív szemidefinit mátrixnak (vagy általánosabban: két pozitív operátornak) legnagyobb közös alsó korlátja. Ebben újfent egy olyan fogalom lesz segítségünkre, amelyet elektromos hálózatok modellezésére vezettek be. Megismerkedünk a párhuzamos összeadás nevű művelettel, és az előző részben megismert fogalmak végtelen dimenziós általánosításaival.
részbenrendezésre nézve mikor van két pozitív szemidefinit mátrixnak (vagy általánosabban: két pozitív operátornak) legnagyobb közös alsó korlátja. Ebben újfent egy olyan fogalom lesz segítségünkre, amelyet elektromos hálózatok modellezésére vezettek be. Megismerkedünk a párhuzamos összeadás nevű művelettel, és az előző részben megismert fogalmak végtelen dimenziós általánosításaival.
1. Portok párhuzamos kapcsolása
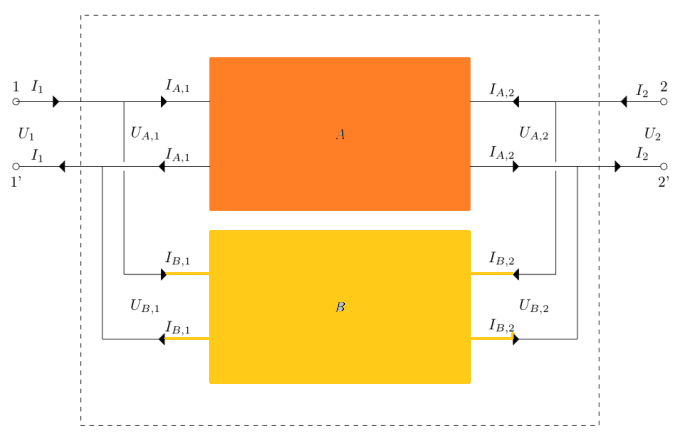
Az előző részben megismerkedtünk a kizárólag ohmos ellenást tartalmazó 2-port fogalmával, és láttuk, hogy annak impedanciája egy ![]() -es mátrixszal írható le. Tekintsünk most két ilyen 2-portot (
-es mátrixszal írható le. Tekintsünk most két ilyen 2-portot (![]() és
és ![]() ), és kössük őket párhuzamosan.
), és kössük őket párhuzamosan.
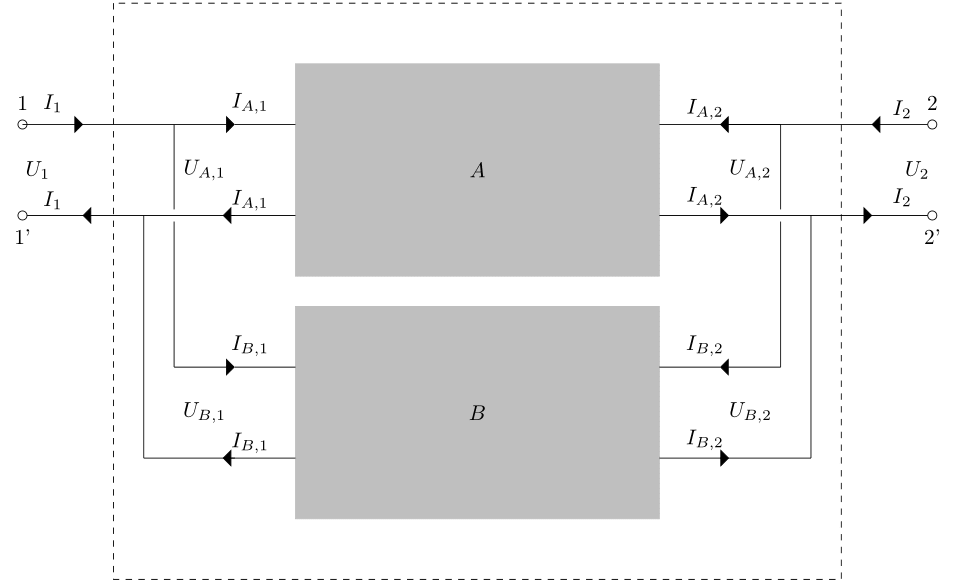
![]() -port hálózatok párhuzamos kapcsolása
-port hálózatok párhuzamos kapcsolása
Mint az ábrán is látható, ez alatt azt értjük, hogy a két hálózat mindegyik port párján a kimenetet a kimenettel, a bemenetet a bemenettel összekötjük. Az így kapott új hálózat szintén egy ![]() -port hálózat, így természetes módon adódik a kérdés, hogy mi a kapcsolt hálózat
-port hálózat, így természetes módon adódik a kérdés, hogy mi a kapcsolt hálózat ![]() impedancia mátrixa, és hogy hogyan számolható az ki a
impedancia mátrixa, és hogy hogyan számolható az ki a ![]() és
és ![]() impedanciák segítségével. Megjegyezzük, hogy
impedanciák segítségével. Megjegyezzük, hogy ![]() -port hálózatok esetén épp a replusz nevű műveletet kapjuk. Azaz ha az 1-portokon az eredő ellenállás
-port hálózatok esetén épp a replusz nevű műveletet kapjuk. Azaz ha az 1-portokon az eredő ellenállás ![]() és
és ![]() volt, akkor a csatolt hálózat eredő ellenállása
volt, akkor a csatolt hálózat eredő ellenállása ![]() . Ez a mennyiség egyébként nem más, mint az
. Ez a mennyiség egyébként nem más, mint az ![]() és
és ![]() valós számok harmonikus közepének a fele.
valós számok harmonikus közepének a fele.
Elsőként nézzünk egy konkrét példát. Válasszuk ![]() -nak az előző részben szereplő 2-portot:
-nak az előző részben szereplő 2-portot:
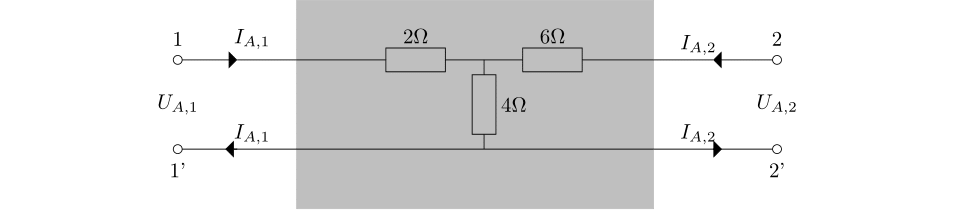
A Kirchhoff-egyenleteket felírva megkaptuk, hogy ennek impedanciája
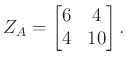
Az egyszerűség kedvéért a ![]() hálózat legyen azonos szerkezetű
hálózat legyen azonos szerkezetű ![]() -val:
-val:
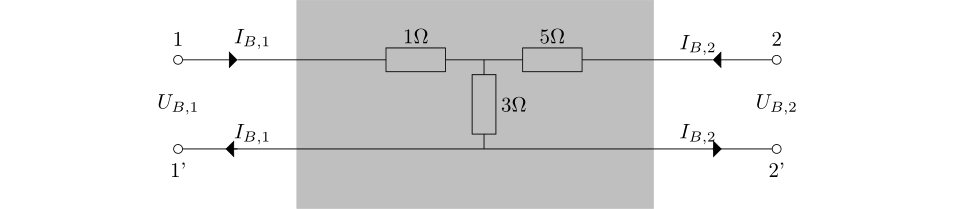
A Kirchoff egyenletek segítségével itt azt kapjuk hogy ![]() impedanciája
impedanciája

Az ezekből adódó párhuzamosan kapcsolt ![]() -port hálózat a következő:
-port hálózat a következő:
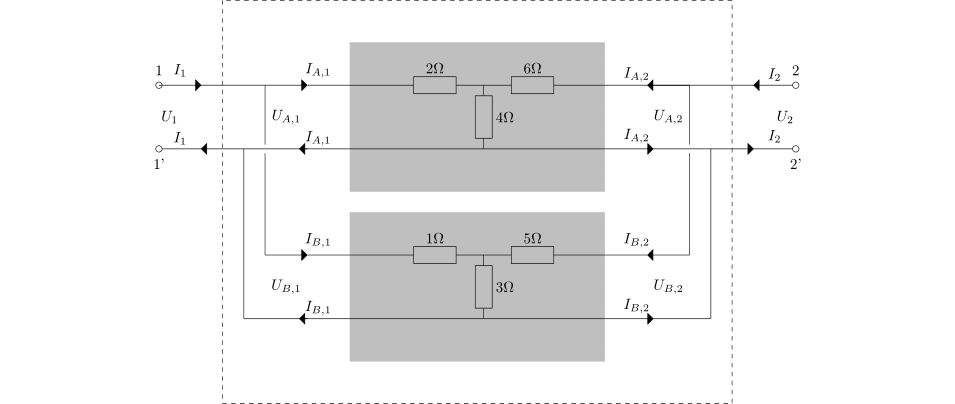
Klasszikus fizikai érveléseket felhasználva a kapott hálózat impedanciája így határozható meg: mindkét hálózatban egy-egy csillag kapcsolás található. Alkalmazzuk ezekre a csillag-delta átalakítást, ekkor két párhuzamosan kapcsolt delta kapcsolásunk lesz. Ez azonos azzal a delta kapcsolással, amelynek minden eleme a két delta megfelelő elemeinek párhuzamos kapcsoltja. Ezekre rendre alkalmazva a két ellenállás párhuzamos kapcsolására ismert képletet, majd az eredő ellenállásokból álló delta kapcsolásra használva a delta-csillag átalakítást, a következő, az eredetivel ekvivalens ![]() -port hálózathoz jutunk:
-port hálózathoz jutunk:
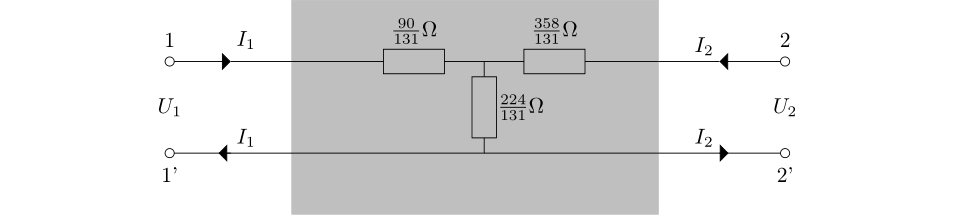
Az ekvivalens hálózat
Innen pedig már az ismert módon kapjuk a Kirchhoff-egyenletekből, hogy
Látjuk tehát (pontosabban el lehet képzelni), hogy a kapcsolt hálózat impedanciájának kiszámításához elég sok számolásra van szükség. Ráadásul olyan számolásra, amely feltételezi, hogy ismerjük a hálózatok konkrét felépítését. Tehát ugyanazzal a nehézséggel találkozunk, mint a cikksorozat első részében. Nem csak a nehézség ugyanaz, annak feloldása is: adjunk olyan képletet, amiben csak a csatolatlan hálózatok impedanciái, és mátrix operációk szerepelnek. Be lehet bizonyítani (a részletektől itt eltekintünk), hogy a párhuzamos kapcsolással nyert hálózat impedanciája
| (1) |
Következésképp, az impedancia meghatározása mindössze három invertálásból és egy összeadásból áll, ezek pedig algoritmikusan elvégezhető feladatok. Ellenőrzésként, a kapott képletbe behelyettesítve valóban azt kapjuk, hogy
Az így nyert műveletet, amely tehát két ![]() -hoz és
-hoz és ![]() -hez
-hez ![]() -t rendeli, párhuzamos összeadásnak nevezzük, és
-t rendeli, párhuzamos összeadásnak nevezzük, és ![]() szimbólummal jelöljük. A képletben invertálás is szerepel, így elsőre nem nyilvánvaló, hogy ez a művelet definiálható pozitív szemidefinit mátrixokra is. Az invertálhatóság problémáján egy egyszerű (határátmenetet alkalmazó) okoskodással felül lehet emelkedni, azonban az (1) formulát biztosan elveszítjük. De mint látni fogjuk, ez nem okoz problémát, mert nem azzal akarunk dolgozni. Sokkal fontosabb, hogy két pozitív operátor
szimbólummal jelöljük. A képletben invertálás is szerepel, így elsőre nem nyilvánvaló, hogy ez a művelet definiálható pozitív szemidefinit mátrixokra is. Az invertálhatóság problémáján egy egyszerű (határátmenetet alkalmazó) okoskodással felül lehet emelkedni, azonban az (1) formulát biztosan elveszítjük. De mint látni fogjuk, ez nem okoz problémát, mert nem azzal akarunk dolgozni. Sokkal fontosabb, hogy két pozitív operátor ![]() párhuzamos összegét definiálhatjuk a kvadratikus alakján keresztül. Azaz legyen
párhuzamos összegét definiálhatjuk a kvadratikus alakján keresztül. Azaz legyen ![]() az az operátor, amelynek kvadratikus alakja
az az operátor, amelynek kvadratikus alakja
| (2) |
Az olvasó egész eddig joggal kérdezhette, hogy mi köze van a párhuzamos kapcsolásnak a cikk témájához, nevezetesen a pozitiv operátorok kúpjának részbenrendezéséhez. Arról nem is beszélve, hogy mi köze az egésznek az operátorok altérre vonatkozó zárlatához, ami pedig a cikksorozat témája.
Helyettesítsünk ![]() helyére 0-t a (2) formulában:
helyére 0-t a (2) formulában: ![]() . Hasonlóan,
. Hasonlóan, ![]() helyettesítéssel azt kapjuk, hogy
helyettesítéssel azt kapjuk, hogy ![]() azaz
azaz ![]() az
az ![]() és
és ![]() operátoroknak egy közös alsó korlátja. Arról, hogy a legnagyobb közös alsó korlát lenne, nincs és nem is lehet szó. Már a legegyszerűbb invertálható mátrix esetben is azt kapjuk, hogy
operátoroknak egy közös alsó korlátja. Arról, hogy a legnagyobb közös alsó korlát lenne, nincs és nem is lehet szó. Már a legegyszerűbb invertálható mátrix esetben is azt kapjuk, hogy ![]() , márpedig
, márpedig ![]() -nak és
-nak és ![]() -nak a legnagyobb közös alsó korlátja nyilvánvalóan
-nak a legnagyobb közös alsó korlátja nyilvánvalóan ![]() . Ennek ellenére ne becsüljük le a műveletnek ezt a közös alsó korlátot kijelölő tulajdonságát. A cikk végére épp azt fogjuk látni, hogy
. Ennek ellenére ne becsüljük le a műveletnek ezt a közös alsó korlátot kijelölő tulajdonságát. A cikk végére épp azt fogjuk látni, hogy ![]() -ban nem feltétlenül van két elemnek legnagyobb közös alsó korlátja, de a párhuzamos összeadás lehetővé teszi, hogy „úgy csináljunk, mintha lenne”. Így például a következő fejezet témáját képező fogalom a vektorhálók elméletéből ismert sáv projekciónak [4] egy imitációja.
-ban nem feltétlenül van két elemnek legnagyobb közös alsó korlátja, de a párhuzamos összeadás lehetővé teszi, hogy „úgy csináljunk, mintha lenne”. Így például a következő fejezet témáját képező fogalom a vektorhálók elméletéből ismert sáv projekciónak [4] egy imitációja.
Mivel a későbbiekben szükségünk lesz rájuk, megemlítjük a párhuzamos összeadás két egyszerűen bizonyítható tulajdonságát:
(a) monoton, azaz ![]() és
és ![]() esetén
esetén ![]() ,
,
(b) minden ![]() és
és ![]() esetén
esetén ![]() .
.
Mielőtt rátérnénk a pozitív operátorok részbenrendezésére, teszünk egy rövid kitérőt.
2. Az operátorképterekre vonatkozó általánosított zárlat
Emlékeztetünk arra, hogy az előző részben az egyszerűség kedvéért végig feltettük, hogy ![]() egy véges dimenziós Hilbert tér. Ha ettől a feltevéstől meg akarunk szabadulni, akkor többet kell megkövetelnünk az
egy véges dimenziós Hilbert tér. Ha ettől a feltevéstől meg akarunk szabadulni, akkor többet kell megkövetelnünk az ![]() altértől, nevezetesen azt, hogy legyen zárt. (Véges dimenziós Hilbert terekben minden lineáris alér zárt, így erről eddig nyugodtan hallgathattunk.)
altértől, nevezetesen azt, hogy legyen zárt. (Véges dimenziós Hilbert terekben minden lineáris alér zárt, így erről eddig nyugodtan hallgathattunk.)
Mivel a vizsgálatok során az ![]() altér szerepét gyakran egy olyan operátorképtér játssza, ami nem zárt, ezért szükségünk van egy olyan általánosításra, ahol az altér zártsága már nincs megkövetelve. Ebben van segítségünkre az imént bevezetett párhuzamos összeadás.
altér szerepét gyakran egy olyan operátorképtér játssza, ami nem zárt, ezért szükségünk van egy olyan általánosításra, ahol az altér zártsága már nincs megkövetelve. Ebben van segítségünkre az imént bevezetett párhuzamos összeadás.
Legyenek ![]() és
és ![]() tetszőleges pozitív operátorok a
tetszőleges pozitív operátorok a ![]() Hilbert téren. Az
Hilbert téren. Az ![]() operátor
operátor ![]() -re (vagy
-re (vagy ![]() képterére) vonatkozó általánosított zárlatán az alábbi
képterére) vonatkozó általánosított zárlatán az alábbi
| (3) |
operátort értjük, ahol a limesz pontonkénti konvergenciában értendő. Az ![]() leképezés tulajdonságaiból itt csak egyet említünk meg, mert azt használni is fogjuk. Ha
leképezés tulajdonságaiból itt csak egyet említünk meg, mert azt használni is fogjuk. Ha ![]() valamilyen
valamilyen ![]() -ra, akkor
-ra, akkor ![]() . Valóban, az (a) és (b) tulajdonságokat kihasználva látszik, hogy
. Valóban, az (a) és (b) tulajdonságokat kihasználva látszik, hogy

Megjegyezzük, hogy ha ![]() egy zárt lineáris altér,
egy zárt lineáris altér, ![]() -pedig az
-pedig az ![]() -re való merőleges vetítés, akkor
-re való merőleges vetítés, akkor ![]() . Tehát a fenti párhuzamos összeadást használó eljárás egy új módszert szolgáltat az
. Tehát a fenti párhuzamos összeadást használó eljárás egy új módszert szolgáltat az ![]() altérre vonatkozó zárlat kiszámítására.
altérre vonatkozó zárlat kiszámítására.
3. Operátorok legnagyobb közös alsó korlátja
Az előző részben homályosan utaltunk arra, hogy a pozitív szemidefinit mátrixok
részbenrendezése meglehetősen komplikált rendezésstruktúrát eredményez. Nevezetesen: még az olyan egyszerű szerkezetű mátrixoknak sem létezik legnagyobb közös alsó korlátja, mint a
 és
és
Másképp megfogalmazva, a
halmaznak nincs legnagyobb eleme, noha az egységmátrix egy nagyon szimpatikus jelölt. A fejezet végén látni fogjuk, hogy valóban nincs legnagyobb elem, elsőként azonban megelégszünk azzal, hogy megmutatjuk, hogy az egységmátrix nem az. Tekintsük az
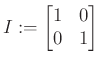 és
és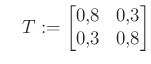
mátrixokat. A sajátértékeket kiszámolva láthatjuk, hogy mindkettő pozitív szemidefinit. Hasonlóan, a ![]() ,
, ![]() ,
, ![]() , és
, és ![]() sajátértékei mind nemnegatívak, így
sajátértékei mind nemnegatívak, így ![]() és
és ![]() benne van a
benne van a ![]() halmazban. Ugyanakkor
halmazban. Ugyanakkor ![]() -nek van negatív sajátértéke, következésképp az
-nek van negatív sajátértéke, következésképp az ![]() egyenlőtlenség nem teljesül, tehát
egyenlőtlenség nem teljesül, tehát ![]() nem legnagyobb eleme
nem legnagyobb eleme ![]() -nek. Pontosan az ilyen össze nem hasonlított elemek okozzák a nehézségeket.
-nek. Pontosan az ilyen össze nem hasonlított elemek okozzák a nehézségeket.
Térjünk vissza az általános problémára. Legyen ![]() egy Hilbert tér, tekintsük a pozitív operátorok
egy Hilbert tér, tekintsük a pozitív operátorok ![]() -val jelölt kúpját. (Ha
-val jelölt kúpját. (Ha ![]() véges dimenziós, akkor
véges dimenziós, akkor ![]() a pozitív szemidefinit mátrixok kúpjának felel meg.) A kérdés, amely hosszú éveken át megválaszolatlanul maradt, a következő: van-e olyan szükséges és elégséges feltétel, amely alapján el tudjuk dönteni, hogy két operátornak létezik-e legnagyobb közös alsó korlátja. (Az érdeklődő olvasó a probléma kvantummechanikai vonatkozásai mellett önmagukban is érdekes eredményeket találhat az [1,5,6] cikkekben.)
a pozitív szemidefinit mátrixok kúpjának felel meg.) A kérdés, amely hosszú éveken át megválaszolatlanul maradt, a következő: van-e olyan szükséges és elégséges feltétel, amely alapján el tudjuk dönteni, hogy két operátornak létezik-e legnagyobb közös alsó korlátja. (Az érdeklődő olvasó a probléma kvantummechanikai vonatkozásai mellett önmagukban is érdekes eredményeket találhat az [1,5,6] cikkekben.)
A kérdésre a teljes választ Tsuyoshi Ando japán matematikus adta meg az 1999-ben megjelent Problem of Infimum in the Positive Cone című cikkében [3].

Megjegyezzük, hogy a ![]() -val jelölt általánosított zárlat fogalma is tőle származik, vagy legalábbis elsők között használta, mint egyfajta kitüntetett operátor (az
-val jelölt általánosított zárlat fogalma is tőle származik, vagy legalábbis elsők között használta, mint egyfajta kitüntetett operátor (az ![]() operátor
operátor ![]() -szerinti abszolút folytonos része [2]). Ando tétele a következőt mondja:
-szerinti abszolút folytonos része [2]). Ando tétele a következőt mondja:
![]() -nak és
-nak és ![]() -nek pontosan akkor létezik legnagyobb közös alsó korlátja, ha
-nek pontosan akkor létezik legnagyobb közös alsó korlátja, ha
Ekkor a legnagyobb közös alsó korlát ![]() és
és ![]() közül a kisebb.
közül a kisebb.
Kiderült tehát, hogy a legnagyobb közös alsó korlát meghatározásához, és általában, a létezésének garantálásához épp az általánosított zárlatra van szükség.
Térjünk vissza a ![]() és
és ![]() mátrixokokkal kapcsolatos problémánkra. Világos, hogy
mátrixokokkal kapcsolatos problémánkra. Világos, hogy ![]() és
és ![]() . A korábbi észrevételünk alapján ebből az következik, hogy
. A korábbi észrevételünk alapján ebből az következik, hogy ![]() és
és ![]() . Mivel azonban
. Mivel azonban ![]() és
és ![]() nem összehasonlítható, a legnagyobb közös alsó korlát nem létezhet.
nem összehasonlítható, a legnagyobb közös alsó korlát nem létezhet.
A cikk mondandóját egy mondatba tömörítve: azt láttuk hogy egy egyszerű mérnöki feladat modellezésének melléktermékeként olyan műveletet nyertünk, amely aztán hasznos fegyverünk volt egy teljesen absztrakt, az eredeti problémához lazán sem kapcsolódó kérdés megválaszolásánál.
A cikksorozat az Emberi Erőforrások Minisztériumának ÚNKP-18-4-BGE-3 kódszámú „Új Nemzeti Kiválóság Program”, és a Nemzeti Fejlesztési, Kutatási és Innovációs Hivatal (NKFIH PD128374 és K115383) támogatásával készül.
Hivatkozások
- [1] W. N. Anderson, Jr. and M. Schreiber, The infima of two projections, Acta Sci. Math. (Szeged) 33(1972), 165–168.
- [2] T. Ando, Lebesgue-type decomposition of positive operators, Acta Sci. Math. (Szeged), 38(1976), 253–260.
- [3] T. Ando, Problem of Infimum in the Positive Cone, In: Rassias T. M., Srivastava H. M. (eds) Analytic and Geometric Inequalities and Applications. Mathematics and Its Applications, vol 478. Springer, Dordrecht (1999).
- [4] S. Bochner and R. S. Phillips, Additive Set Functions and Vector Lattices, Annals of Mathematics, Second Series, Vol. 42, No. 1, (1941), 316–324
- [5] S. Gudder, Lattice properties of quantum effects, J. Math. Phys., 37(1996), 2637–2642.
- [6] T. Moreland and S. Gudder, Infima of Hilbert space effects, Linear Algebra and its Applications, 286 (1–3), 1999, 1–17
és Budapesti Gazdasági Egyetem