Egy kvantumcsoport elsősorban is egy Hopf-algebra, egy gyönyörű struktúra, amelynek elegáns definiáló axiómáit már az 1940-es években leírták, sokkal korábban minthogy az 1980-as években az igazán fontos fizikából érkező példák megjelentek volna. Kezdjük tehát ezen elegáns axiómák ismertetésével, észbentartva azt, hogy a modern példák és a további struktúrák azok, amik igazán érdekessé és fontossá teszik ezt a témakört. Egy ![]() Hopf-algebra tehát a következő axiómákat teljesíti:
Hopf-algebra tehát a következő axiómákat teljesíti:
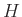 egy
egy 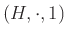
 test feletti egységelemes algebra.
test feletti egységelemes algebra. egy
egy 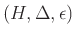
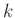 test feletti koegységelemes koalgebra. A
test feletti koegységelemes koalgebra. A 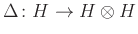 „koszorzás” és az
„koszorzás” és az 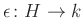 „koegység” leképezéseknek teljesíteni kell a
„koegység” leképezéseknek teljesíteni kell a  és
és 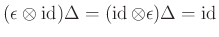 azonosságokat.
azonosságokat.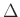 és
és 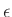 algebra homomorfizmusok.
algebra homomorfizmusok.- Létezik egy
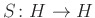 „antipodális” leképezés, mely teljesíti a
„antipodális” leképezés, mely teljesíti a 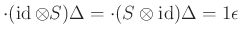 azonosságot.
azonosságot.
Három nézőpontból érhetünk (egymástól függetlenül) a fenti axiómákhoz; ezek mindegyike a kvantumcsoport egy definícióját adja. Alább mindhármat tárgyaljuk, de helyszűke miatt nagyrészt az elsőre fogunk fókuszálni.
Az első megközelítés avval az észrevétellel kezdődik, hogy egy ![]() véges csoport
véges csoport ![]() függvényei vagy egy
függvényei vagy egy ![]() algebrai csoport
algebrai csoport ![]() koordináta-algebrája Hopf-algebrákat alkotnak. Valóban, egy véges
koordináta-algebrája Hopf-algebrákat alkotnak. Valóban, egy véges ![]() halmazra legyen
halmazra legyen ![]() a
a ![]() -n értelmezett
-n értelmezett ![]() értékű függvények algebrája a pontonkénti műveletekkel ellátva. Azonosítsuk
értékű függvények algebrája a pontonkénti műveletekkel ellátva. Azonosítsuk ![]() -t
-t ![]() -vel, vagyis a kétváltozós függvényekkel. Amikor
-vel, vagyis a kétváltozós függvényekkel. Amikor ![]() valójában egy csoport, egy
valójában egy csoport, egy ![]() elemre legyen
elemre legyen
ahol ![]() a
a ![]() csoport egységeleme és
csoport egységeleme és ![]() tetszőleges. A csoportstruktúra tehát a
tetszőleges. A csoportstruktúra tehát a ![]() koalgebra-struktúrában és az
koalgebra-struktúrában és az ![]() antipodális leképezésben van elkódolva. Hasonlóan, minden
antipodális leképezésben van elkódolva. Hasonlóan, minden ![]() polinom-egyenletekkel megadott részhalmazra egy
polinom-egyenletekkel megadott részhalmazra egy ![]() „koordináta-algebrát” definiálhatunk, mint a
„koordináta-algebrát” definiálhatunk, mint a ![]() -en értelmezett polinom-függvények tere, moduló a
-en értelmezett polinom-függvények tere, moduló a ![]() mentén eltűnő függvények ideálja. Amennyiben
mentén eltűnő függvények ideálja. Amennyiben ![]() algebrailag zárt, ilymódon egy pontos (funktoriális) megfeletetést kapunk ilyen polinomiális részhalmazok és nilpotens-mentes végesen generált kommutatív algebrák között. Amikor a
algebrailag zárt, ilymódon egy pontos (funktoriális) megfeletetést kapunk ilyen polinomiális részhalmazok és nilpotens-mentes végesen generált kommutatív algebrák között. Amikor a ![]() részhalmaz egy csoportot alkot és a csoportművelet polinomiális, a
részhalmaz egy csoportot alkot és a csoportművelet polinomiális, a ![]() szorzás-leképezés e megfeleltetés mentén egy, épp az ellenkező irányba mutató
szorzás-leképezés e megfeleltetés mentén egy, épp az ellenkező irányba mutató ![]() algebra homomorfizmust ad. Hasonló módon kaphatók a Hopf-algebra struktúra további elemei. Íme két példa: Az „affin egyenes” a
algebra homomorfizmust ad. Hasonló módon kaphatók a Hopf-algebra struktúra további elemei. Íme két példa: Az „affin egyenes” a ![]() koordináta-algebrával (egyváltozós polinomokkal) adható meg, ahol a
koordináta-algebrával (egyváltozós polinomokkal) adható meg, ahol a ![]() additív koszorzat a
additív koszorzat a ![]() -beli összeadásnak felel meg. Az olvasóra hagyjuk a struktúra további részeinek definícióját, és így annak megmutatását, hogy minden
-beli összeadásnak felel meg. Az olvasóra hagyjuk a struktúra további részeinek definícióját, és így annak megmutatását, hogy minden ![]() testre létezik Hopf-algebra. A „kör” hasonló módon írható le, véve a
testre létezik Hopf-algebra. A „kör” hasonló módon írható le, véve a ![]() koordináta-algebrát (vagyis
koordináta-algebrát (vagyis ![]() -beli és
-beli és ![]() -beli polinomokat, amelyekre a
-beli polinomokat, amelyekre a ![]() relációk teljesülnek), ellátva a
relációk teljesülnek), ellátva a ![]() multiplikatív koszorzással, ami a
multiplikatív koszorzással, ami a ![]() -beli szorzásnak felel meg. A további részleteket és az ellenőrzést ismét az olvasóra bízzuk. A legismertebb komplex Lie-algebrák általában polinom-egyenletekkel definiáltak, amelyekhez természetesen tartozik a
-beli szorzásnak felel meg. A további részleteket és az ellenőrzést ismét az olvasóra bízzuk. A legismertebb komplex Lie-algebrák általában polinom-egyenletekkel definiáltak, amelyekhez természetesen tartozik a ![]() algebra, illetve definiálhatók általános
algebra, illetve definiálhatók általános ![]() test felett a megfelelő hasonló egyenletekkel és a
test felett a megfelelő hasonló egyenletekkel és a ![]() algebrával. A
algebrával. A ![]() feletti esetben egy „valós forma” egy további struktúrát, egy kompatibilis, komplex lineáris involúciót jelent, amellyel a koordináta algebra egy
feletti esetben egy „valós forma” egy további struktúrát, egy kompatibilis, komplex lineáris involúciót jelent, amellyel a koordináta algebra egy ![]() -algebrává válik. Ezekkel a jelölésekkel a fenti két példa
-algebrává válik. Ezekkel a jelölésekkel a fenti két példa ![]() és
és ![]() lesz, és
lesz, és ![]() illetve
illetve ![]() lesz a valós forma.
lesz a valós forma.
Egy általános ![]() Hopf-algebrára is megvannak a
Hopf-algebrára is megvannak a ![]() struktúrák, de általában nem tesszük fel, hogy — mint a fenti példákban —
struktúrák, de általában nem tesszük fel, hogy — mint a fenti példákban — ![]() algebrája kommutatív. Ez épp a nemkommutatív geometria vagy „kvantálás” nézőpontja egy kommutatív koordináta-algebra vagy függvényalgebra nemkommutatív deformálására a matematikusok (de nem a fizikusok) értelmezésében. A csoportelmélet, illetve a Lie-csoportok elméletének nagy része erre a szintre emelhető; például amennyiben az
algebrája kommutatív. Ez épp a nemkommutatív geometria vagy „kvantálás” nézőpontja egy kommutatív koordináta-algebra vagy függvényalgebra nemkommutatív deformálására a matematikusok (de nem a fizikusok) értelmezésében. A csoportelmélet, illetve a Lie-csoportok elméletének nagy része erre a szintre emelhető; például amennyiben az
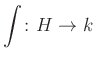
eltolás-invariáns integrálás (ami bizonyos értelemben ![]() -t is használja) létezik, akkor átskálázás erejéig egyértelmű, és valójában a szép esetekben létezik is. Hasonlóan, az
-t is használja) létezik, akkor átskálázás erejéig egyértelmű, és valójában a szép esetekben létezik is. Hasonlóan, az ![]() komplex differenciálformák minden
komplex differenciálformák minden ![]() algebra felett értelmezhetőek. Az egy fokú
algebra felett értelmezhetőek. Az egy fokú ![]() 1-formák tere egy
1-formák tere egy ![]() bimodulus, amelyen egy
bimodulus, amelyen egy ![]() operátor is adott, ami eleget tesz a
operátor is adott, ami eleget tesz a ![]() (
(![]() ) Leibniz-szabálynak és
) Leibniz-szabálynak és ![]() . Ez kicsit gyengébb mint a szokásos differenciálgeometriában, még akkor is, amikor
. Ez kicsit gyengébb mint a szokásos differenciálgeometriában, még akkor is, amikor ![]() kommutatív, mivel nem követeljük meg, hogy az 1-formák kommutáljanak
kommutatív, mivel nem követeljük meg, hogy az 1-formák kommutáljanak ![]() elemeivel. Amikor
elemeivel. Amikor ![]() egy Hopf-algebra, megkövetelhető az is, hogy
egy Hopf-algebra, megkövetelhető az is, hogy ![]() eltolás-invariáns legyen, ismét egy a
eltolás-invariáns legyen, ismét egy a ![]() -t is használó értelemben. Ebben az értelemben egy „kvantumcsoport” nem egyszerűen egy Hopf-algebra, hanem egy további, a Lie-csoportokhoz hasonló struktúrája is van. E mélyebb elmélet néhány tulajdonsága már az egyenes és a kör példáján is látható, bár ezek a példák kommutatívak mint algebrák. Az egyszerű (tehát valódi hányados nélküli) eltolás-invariáns
-t is használó értelemben. Ebben az értelemben egy „kvantumcsoport” nem egyszerűen egy Hopf-algebra, hanem egy további, a Lie-csoportokhoz hasonló struktúrája is van. E mélyebb elmélet néhány tulajdonsága már az egyenes és a kör példáján is látható, bár ezek a példák kommutatívak mint algebrák. Az egyszerű (tehát valódi hányados nélküli) eltolás-invariáns ![]() struktúrák például osztályozhatók.
struktúrák például osztályozhatók. ![]() esetén egy
esetén egy ![]() paraméterrel jellemezhetők, és a
paraméterrel jellemezhetők, és a
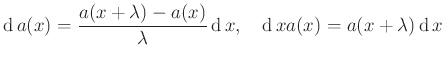
véges differencia alakra hozhatók minden ![]() -re. Csak
-re. Csak ![]() esetén fog
esetén fog ![]() a függvényekkel kommutálni, tehát csak ekkor látjuk a megszokott geometriát.
a függvényekkel kommutálni, tehát csak ekkor látjuk a megszokott geometriát. ![]() esetén az eltolás-invariáns
esetén az eltolás-invariáns ![]() struktúrákat egy
struktúrákat egy ![]() érték klasszifikál, és ekkor
érték klasszifikál, és ekkor
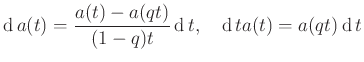
minden ![]() -re. Ez a két példa valójában bemutatja a ma ismert kvantumcsoportok két fő típusát. A legnevezetesebb példa a
-re. Ez a két példa valójában bemutatja a ma ismert kvantumcsoportok két fő típusát. A legnevezetesebb példa a ![]() „
„![]() -deformált” kvantumcsoport, melynek
-deformált” kvantumcsoport, melynek ![]() generátoraira a relációk és a koszorzat a következő módon adható meg:
generátoraira a relációk és a koszorzat a következő módon adható meg:

ahol mátrix-szorzást alkalmazunk (vagyis például ![]() , stb.). Hasonlóan adhatók meg a
, stb.). Hasonlóan adhatók meg a ![]() változatok minden
változatok minden ![]() Lie-csoportra, illetve komplexifikáltjaikra. Másfajta „
Lie-csoportra, illetve komplexifikáltjaikra. Másfajta „![]() -deformációra” ad példát
-deformációra” ad példát ![]() , amit a
, amit a ![]() (
(![]() ) elemek által generált algebraként definiálunk; a relációk
) elemek által generált algebraként definiálunk; a relációk ![]() ; és az additív koszorzat úgy adható meg, mint
; és az additív koszorzat úgy adható meg, mint ![]() esetében. Ez valójában egy feloldható Lie-algebra burkoló algebrája (lásd később). A NASA GLAST műhold mérései alapján azt is tesztelni tudjuk majd esetleg, hogy a mi téridőnk ilyen-e,
esetében. Ez valójában egy feloldható Lie-algebra burkoló algebrája (lásd később). A NASA GLAST műhold mérései alapján azt is tesztelni tudjuk majd esetleg, hogy a mi téridőnk ilyen-e, ![]() szekundum választással, ahol ez a hatás a kvantumgravitációból jönne. További nemtriviális példákat adnak a „bikeresztszorzat” kvantumcsoportok, amelyeket később fogunk érinteni.
szekundum választással, ahol ez a hatás a kvantumgravitációból jönne. További nemtriviális példákat adnak a „bikeresztszorzat” kvantumcsoportok, amelyeket később fogunk érinteni.
A kvantumcsoportok definíciójának második megközelítése azon az észrevételen alapul, hogy egy tetszőleges csoport ![]() csoportalgebrája, és egy tetszőleges Lie-algebra
csoportalgebrája, és egy tetszőleges Lie-algebra ![]() burkoló algebrája Hopf-algebrákat alkotnak, ez esetben szimmetrikus koszorzattal (vagyis koalgebrájuk „kokommutatív”). Egy
burkoló algebrája Hopf-algebrákat alkotnak, ez esetben szimmetrikus koszorzattal (vagyis koalgebrájuk „kokommutatív”). Egy ![]() csoport
csoport ![]() feletti csoportalgebrája egyszerűen a
feletti csoportalgebrája egyszerűen a ![]() elemei mint bázis által definiált vektortér, és a szorzat a báziselemeken a
elemei mint bázis által definiált vektortér, és a szorzat a báziselemeken a ![]() -beli szorzat, lineárisan kiterjesztve. Továbbá
-beli szorzat, lineárisan kiterjesztve. Továbbá
minden ![]() -re, ismét lineárisan kiterjesztve. Hasonlóan, legyen
-re, ismét lineárisan kiterjesztve. Hasonlóan, legyen ![]() egy Lie-algebra a
egy Lie-algebra a ![]() Lie-zárójellel ellátva. Az
Lie-zárójellel ellátva. Az ![]() egy egyszerű (de nem túlzottan elegáns) definíciója a következő: vegyük
egy egyszerű (de nem túlzottan elegáns) definíciója a következő: vegyük ![]() egy bázisát és legyen
egy bázisát és legyen ![]() az a szabad asszociatív algebra, amelyet ezek az elemek mint generátorok adnak, és vegyük ehhez a
az a szabad asszociatív algebra, amelyet ezek az elemek mint generátorok adnak, és vegyük ehhez a ![]() relációkat minden
relációkat minden ![]() báziselemre. Mindez lineárisan kiterjed, így ez az egyenlet minden
báziselemre. Mindez lineárisan kiterjed, így ez az egyenlet minden ![]() elemre teljesül. A koszorzás ismét az additív koszorzás:
elemre teljesül. A koszorzás ismét az additív koszorzás: ![]() a generátorokon. Ezekben a példákban a
a generátorokon. Ezekben a példákban a ![]() vagy az
vagy az ![]() algebra egy hatása a
algebra egy hatása a ![]() csoport vagy a
csoport vagy a ![]() Lie-algebra egy lineáris hatásával egyenértékű, és
Lie-algebra egy lineáris hatásával egyenértékű, és ![]() azt kódolja el, hogy a hatások hogyan terjednek ki a tenzorszorzatokra; hasonlóan ahhoz, ahogy egy
azt kódolja el, hogy a hatások hogyan terjednek ki a tenzorszorzatokra; hasonlóan ahhoz, ahogy egy ![]() Hopf-algebrát tekinthetünk úgy, mint egy „általánosított szimmetriát”, ahol a
Hopf-algebrát tekinthetünk úgy, mint egy „általánosított szimmetriát”, ahol a ![]() elem
elem ![]() -val hat a tenzorszorzaton. Erre szükségünk van például akkor, amikor meg akarjuk határozni, hogy egy másik algebra kovariáns-e
-val hat a tenzorszorzaton. Erre szükségünk van például akkor, amikor meg akarjuk határozni, hogy egy másik algebra kovariáns-e ![]() -ra nézve.
-ra nézve.
A leghíresebb példa pedig ![]() , amelyet az
, amelyet az ![]() generátorokkal adhatunk meg, és amelyekre a következő relációk teljesülnek:
generátorokkal adhatunk meg, és amelyekre a következő relációk teljesülnek:
![$\displaystyle q^heq^{-h} = q^2e, \ q^hf q^{-h} = q^{-2}f, \ [e, f] = \frac{q^h - q^{-h}}{q -q^{-1}},
$](/images/stories/latex/stipsiczandrasmiisegykvantumcsoport/img91.png)
Megköveteljük továbbá, hogy ![]() .
. ![]() pedig tetszőleges
pedig tetszőleges ![]() esetén egy szimmetrizálható Cartan-mátrixszal definiálható. Ezek a kvantumcsoportok nagyon gazdag algebrai struktúrával rendelkeznek, amelyek csomó- és 3-sokaság-invariánsokhoz vezetnek. Az egyik legmélyebb eredmény a Lusztig–Kashiwara kanonikus bázis létezése, amely a legmagasabb súlyú modulusoknak indukálja egy bázisát; ez az eredmény még a
esetén egy szimmetrizálható Cartan-mátrixszal definiálható. Ezek a kvantumcsoportok nagyon gazdag algebrai struktúrával rendelkeznek, amelyek csomó- és 3-sokaság-invariánsokhoz vezetnek. Az egyik legmélyebb eredmény a Lusztig–Kashiwara kanonikus bázis létezése, amely a legmagasabb súlyú modulusoknak indukálja egy bázisát; ez az eredmény még a ![]() klasszikus esetben is nagyon fontos.
klasszikus esetben is nagyon fontos.
A harmadik nézőpont szerint Hopf-algebrák az Abel-csoportok utáni legegyszerűbb olyan kategóriát alkotják, amelyben van Fourier-transzformált. E nézőpont adja az önduális formákhoz tartozó „bikeresztszorzat” kvantumcsoportok meglehetősen nagy osztályát. Ezek egyszerre „koordináta-” és „szimmetria-” algebrák, és szoros kapcsolatban állnak a kvantummechanikával. Ezekre egy példa ![]() mely a
mely a ![]() fent tárgyalt nemkommutatív tér–idő algebra Poincaré- kvantumcsoportja. Ez esetben a speciális relativitáselmélet ugyanúgy alkalmazható, de mint kvantumcsoport szimmetria. Ez a kvantumcsoport úgy is interpretálható, mint egy feketelyuk-szerű tulajdonságokkal rendelkező görbült térben mozgó részecske kvantálása.
fent tárgyalt nemkommutatív tér–idő algebra Poincaré- kvantumcsoportja. Ez esetben a speciális relativitáselmélet ugyanúgy alkalmazható, de mint kvantumcsoport szimmetria. Ez a kvantumcsoport úgy is interpretálható, mint egy feketelyuk-szerű tulajdonságokkal rendelkező görbült térben mozgó részecske kvantálása.
Shahn Majid
További olvasmány:
S. Majid, A Quantum Groups Primer, L. M. S. Lect. Notes 292, 2002.
Shahn Majid a Queen Mary (University of London) matematika professzora; e-mail címe Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.. A cikk eredetileg az American Mathematical Society Notices folyóiratának 2006-os számában jelent meg a What is ...? rovatban. A fordítást Stipsicz András készítette.
Sahn Majid, WHAT IS...a Quantum Group? Notices Amer. Math. Soc. Vol. 53 Num. 1 (January, 2006) 30-31 ©2006 American Mathematical Society









