Egyenletrendszerek megoldásai, így áttételesen az algebrai varietások vizsgálata a matematika egyik legrégebbi problémája. A számelmélet sok alapvető kérdése nyilvánvaló módon átfogalmazható egy ![]() algebrai varietás racionális pontjainak létezésére vonatkozó kérdéssé. Például, az előző lapszámban Tóth Árpád cikkében taglalt, A. Wiles által 1994-ben belátott nagy Fermat-sejtés azzal ekvivalens, hogy az
algebrai varietás racionális pontjainak létezésére vonatkozó kérdéssé. Például, az előző lapszámban Tóth Árpád cikkében taglalt, A. Wiles által 1994-ben belátott nagy Fermat-sejtés azzal ekvivalens, hogy az
egyenlet által meghatározott görbének nincs nem-triviális (az ![]() és
és ![]() triviális megoldásoktól különböző) megoldása
triviális megoldásoktól különböző) megoldása ![]() felett; ennek köze van az e lapszámban részletesen vizsgált
felett; ennek köze van az e lapszámban részletesen vizsgált
egyenletű elliptikus görbék tulajdonságaihoz. Az együtthatók legkisebb közös többszörösével beszorozva látható, hogy minden ![]() -együtthatós egyenletrendszer ekvivalens egy
-együtthatós egyenletrendszer ekvivalens egy ![]() -együtthatóssal. Amennyiben az egyenletrendszer homogén polinomokból áll (azaz minden tag össz-fokszáma megegyezik, mint pl. a Fermat-egyenletben), akkor az így kapott varietás projektív lesz: mivel ekkor minden
-együtthatóssal. Amennyiben az egyenletrendszer homogén polinomokból áll (azaz minden tag össz-fokszáma megegyezik, mint pl. a Fermat-egyenletben), akkor az így kapott varietás projektív lesz: mivel ekkor minden ![]() megoldás és minden 0-tól különböző
megoldás és minden 0-tól különböző ![]() testbeli elemre
testbeli elemre ![]() is nyilván megoldás, ezért a „lényegesen” különböző (tehát, nem csak egy megoldáshármas minden elemét ugyanazzal az állandóval megszorozva kapott) megoldásokat úgy nyerjük, hogy a teljes megoldás-halmazt a
is nyilván megoldás, ezért a „lényegesen” különböző (tehát, nem csak egy megoldáshármas minden elemét ugyanazzal az állandóval megszorozva kapott) megoldásokat úgy nyerjük, hogy a teljes megoldás-halmazt a ![]() multiplikatív csoporttal leosztjuk. Az így kapott megoldáshalmaz esetünkben a
multiplikatív csoporttal leosztjuk. Az így kapott megoldáshalmaz esetünkben a
racionális projektív sík részhalmaza. Hasonló érvelés bármely változószámú, csupa homogén polinomból álló rendszerre is érvényes, azzal a különbséggel hogy a megoldás-halmaz esetleg valamely ![]() -től eltérő dimenziós projektív tér része. Amennyiben az egyenleteink nem homogének, akkor egy egyszerű eljárással azzá tehetők: bevezetünk egy új változót, és minden monomot megszorzunk az új változó valamely hatványával. Az elliptikus görbe esetében például
-től eltérő dimenziós projektív tér része. Amennyiben az egyenleteink nem homogének, akkor egy egyszerű eljárással azzá tehetők: bevezetünk egy új változót, és minden monomot megszorzunk az új változó valamely hatványával. Az elliptikus görbe esetében például ![]() -vel jelölve az új változót ennek eredménye az
-vel jelölve az új változót ennek eredménye az
egyenlet. Természetesen, ezt az új változó lehető legalacsonyabb hatványaival hajtjuk végre.
Adott egész-együtthatós egyenletrendszer esetén bármely ![]() prímhatványra redukcióval származtathatunk egy
prímhatványra redukcióval származtathatunk egy ![]() -együtthatós egyenletrendszert, ahol
-együtthatós egyenletrendszert, ahol ![]() a
a ![]() -elemű véges testet jelöli. Szintén érdekes kérdés az így nyert algebrai egyenletrendszerek megoldhatósága egyre bővebb véges testekben: az úgynevezett Hasse-elv értelmében ilyen (és valós) megoldások bizonyos rendszereiből ugyanis néha konstruálható egész értékű megoldás. Az egyenletrendszert ismét tekinthetjük egy
-elemű véges testet jelöli. Szintén érdekes kérdés az így nyert algebrai egyenletrendszerek megoldhatósága egyre bővebb véges testekben: az úgynevezett Hasse-elv értelmében ilyen (és valós) megoldások bizonyos rendszereiből ugyanis néha konstruálható egész értékű megoldás. Az egyenletrendszert ismét tekinthetjük egy ![]() algebrai varietás definiáló egyenleteinek
algebrai varietás definiáló egyenleteinek ![]() felett. A véges testek feletti eset előnye, hogy a megoldás létezésén túl azok számát is vizsgálhatjuk, azaz bevezethetünk egy
felett. A véges testek feletti eset előnye, hogy a megoldás létezésén túl azok számát is vizsgálhatjuk, azaz bevezethetünk egy
leszámláló-függvényt, ahol ![]() az
az ![]() definiáló egyenleteinek
definiáló egyenleteinek ![]() feletti megoldás-halmazát jelöli.
feletti megoldás-halmazát jelöli.
Egy ![]() feletti
feletti ![]() algebrai varietáshoz természetes és egyértelmű módon társítható egy komplex algebrai varietás is: az azt megadó egyenletrendszer komplex test feletti megoldásainak halmaza. Egy sima komplex algebrai varietáson viszont többek között természetes módon adott egy
algebrai varietáshoz természetes és egyértelmű módon társítható egy komplex algebrai varietás is: az azt megadó egyenletrendszer komplex test feletti megoldásainak halmaza. Egy sima komplex algebrai varietáson viszont többek között természetes módon adott egy ![]() komplex analitikus sokaság-struktúra is: ez azt jelenti, hogy minden pontjának egy elegendően szűk környezetében bevezethetők a megszokott
komplex analitikus sokaság-struktúra is: ez azt jelenti, hogy minden pontjának egy elegendően szűk környezetében bevezethetők a megszokott ![]() -dimenziós komplex vektortéréhez hasonló
-dimenziós komplex vektortéréhez hasonló ![]() koordináták. Amennyiben
koordináták. Amennyiben ![]() teljesít egy topologikus feltételt (az összefüggőséget), akkor az itt szereplő
teljesít egy topologikus feltételt (az összefüggőséget), akkor az itt szereplő ![]() érték független a tekintett ponttól, és
érték független a tekintett ponttól, és ![]() dimenziójának nevezzük. Ha pedig
dimenziójának nevezzük. Ha pedig ![]() projektív, akkor a kapott
projektív, akkor a kapott ![]() kompakt. A továbbiakban
kompakt. A továbbiakban ![]() -ről feltesszük, hogy sima és projektív.
-ről feltesszük, hogy sima és projektív.
A fentiek alapján vizsgálhatjuk az ![]() -hez rendelt
-hez rendelt ![]() komplex analitikus sokaságon az ilyen sokaságokhoz rendelt algebrai invariánsokat. Az egyik ilyen invariáns-fajta az úgynevezett komplex együtthatós de Rham kohomológia-csoportok, amelyek valójában véges dimenziós komplex vektorterek. Konkrétan, minden
komplex analitikus sokaságon az ilyen sokaságokhoz rendelt algebrai invariánsokat. Az egyik ilyen invariáns-fajta az úgynevezett komplex együtthatós de Rham kohomológia-csoportok, amelyek valójában véges dimenziós komplex vektorterek. Konkrétan, minden ![]() komplex
komplex ![]() -dimenziós sokasághoz és
-dimenziós sokasághoz és ![]() számhoz tartozik egy
számhoz tartozik egy ![]() véges dimenziós komplex vektortér. A de Rham-kohomológia értelmezéséhez szükség van az úgynevezett komplex-értékű
véges dimenziós komplex vektortér. A de Rham-kohomológia értelmezéséhez szükség van az úgynevezett komplex-értékű ![]() -adfokú differenciál-forma fogalmára. Lokális komplex analitikus koordinátákban egy
-adfokú differenciál-forma fogalmára. Lokális komplex analitikus koordinátákban egy ![]() -forma egy
-forma egy
alakú kifejezés valamely sima ![]() komplex-értékű függvényekre, ahol az összegzés az összes lehetséges
komplex-értékű függvényekre, ahol az összegzés az összes lehetséges
felbontásra1, és
vektorokra fut. Rögzített ![]() pár esetén a megfelelő
pár esetén a megfelelő ![]() formát tiszta
formát tiszta ![]() -típusúnak nevezzük; komplex analitikus sokaságon egy
-típusúnak nevezzük; komplex analitikus sokaságon egy ![]() -forma
-forma ![]() -típusú része jól meghatározott (azaz, a lokális koordinátarendszer választásától független). Az
-típusú része jól meghatározott (azaz, a lokális koordinátarendszer választásától független). Az ![]() -n értelmezett
-n értelmezett ![]() -formák vektorterét
-formák vektorterét ![]() -val, a tiszta
-val, a tiszta ![]() -típusú formák vektorterét pedig
-típusú formák vektorterét pedig ![]() -val jelöljük. Minden, a (2) egyenletet teljesítő rögzített
-val jelöljük. Minden, a (2) egyenletet teljesítő rögzített ![]() számhármas esetén természetesen adódik tehát egy
számhármas esetén természetesen adódik tehát egy
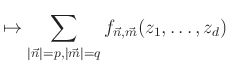 d d |
projektor, ahol ![]() lokálisan (1) által adott, és a fenti összegzés az összes rögzített
lokálisan (1) által adott, és a fenti összegzés az összes rögzített ![]() hosszúságú
hosszúságú ![]() vektorra fut. A
vektorra fut. A ![]() leképezés globális jól-definiáltsága a komplex sokaság-struktúrából következik.
leképezés globális jól-definiáltsága a komplex sokaság-struktúrából következik.
Mivel minden komplex analitikus sokaság egyúttal valós analitikus sokaság is, emiatt értelmezhető a differenciál-formákon egy természetes elsőrendű lineáris differenciál-operátor, a külső deriválás. Bizonyos értelemben a külső deriválás analóg a szemléletes geometriai perem-fogalmunkkal: ahogyan egy ![]() -dimenziós szimpliciális komplexus pereme egy
-dimenziós szimpliciális komplexus pereme egy ![]() -dimenziós szimpliciális komplexus, éppúgy egy
-dimenziós szimpliciális komplexus, éppúgy egy ![]() differenciál-forma külső deriváltja egy
differenciál-forma külső deriváltja egy ![]() -edfokú d
-edfokú d![]() differenciál-forma. Vagyis, minden
differenciál-forma. Vagyis, minden ![]() -ra adódik
-ra adódik
d![]()
Egy komplex sokaság esetében ennek az operátornak a konkrét alakját a linearitás miatt elegendő (1) egy tagjára megadni:
| d |
|
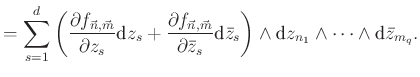 |
Az itt szereplő differenciálások a szokásos ![]() valós-képzetes felbontásban a
valós-képzetes felbontásban a
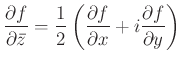
Cauchy—Riemann operátor, valamint annak konjugáltja:
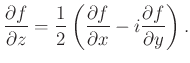
Ahhoz, hogy a külső deriváltban kapott d![]() és d
és d![]() formákkal bővített rendszert újra növekvő sorrendbe rendezhessük, a következő relációkat használhatjuk:
formákkal bővített rendszert újra növekvő sorrendbe rendezhessük, a következő relációkat használhatjuk:
| d |
||
| d |
||
| d |
Azt mondjuk, hogy ![]() zárt, ha d
zárt, ha d![]() , és
, és ![]() egzakt, ha
egzakt, ha ![]() d
d![]() valamely
valamely ![]() formára. Kiderül, hogy minden egzakt forma zárt, ennek fordítottja azonban általában nem igaz. A
formára. Kiderül, hogy minden egzakt forma zárt, ennek fordítottja azonban általában nem igaz. A ![]() -adik de Rham-kohomológia csoport pontosan azt méri, hogy ez mennyire nem teljesül: a
-adik de Rham-kohomológia csoport pontosan azt méri, hogy ez mennyire nem teljesül: a ![]() vektorér definíció szerint a zárt
vektorér definíció szerint a zárt ![]() -formák vektortere leosztva az egzakt
-formák vektortere leosztva az egzakt ![]() -formák vektorterével.
-formák vektorterével.
Algebrailag az előbb bevezetett hányados minden további meggondolás nélkül értelmes, az azonban nem világos, hogy véges dimenziós-e. Ennek megvizsgálásához hasznos W. Hodge tétele, amely kimondja, hogy a fenti hányados izomorf egy bizonyos ![]() -en adott másodrendű elliptikus lineáris parciális differenciál-egyenlet
-en adott másodrendű elliptikus lineáris parciális differenciál-egyenlet ![]() megoldásterével. Az derül ki ugyanis, hogy ha
megoldásterével. Az derül ki ugyanis, hogy ha ![]() sima projektív, akkor az
sima projektív, akkor az ![]() komplex analitikus sokaságra a projektív térről egy speciális tulajdonságokkal rendelkező, úgynevezett Kähler-metrika öröklődik. A Kähler-metrika segítségével bevezethetjük az úgynevezett
komplex analitikus sokaságra a projektív térről egy speciális tulajdonságokkal rendelkező, úgynevezett Kähler-metrika öröklődik. A Kähler-metrika segítségével bevezethetjük az úgynevezett
Hodge—Laplace operátort a ![]() téren, ahol d
téren, ahol d![]() -vel d adjungált operátorát jelöljük az
-vel d adjungált operátorát jelöljük az ![]() metrikára. A következő eredmény ma már klasszikusnak számít [5]:
metrikára. A következő eredmény ma már klasszikusnak számít [5]:

A ![]() elemeit
elemeit ![]() feletti harmonikus
feletti harmonikus ![]() -formáknak nevezzük. A kompakt sokaságokon definiált elliptikus lineáris parciális differenciálegyenletek általános elmélete ekkor garantálja, hogy
-formáknak nevezzük. A kompakt sokaságokon definiált elliptikus lineáris parciális differenciálegyenletek általános elmélete ekkor garantálja, hogy ![]() de Rham kohomológia-terei véges dimenziósak.
de Rham kohomológia-terei véges dimenziósak.
A külső deriválásnak minden komplex sokaságon van egy természetes felbontása
d![]()
alakban, ahol minden ![]() esetén
esetén
Hasonlóan a Hodge—Laplace operátorhoz, bevezethetjük a
Dolbeault—Laplace operátort. Könnyen látszik, hogy ez az operátor egy tiszta ![]() -típusú formát ugyanilyen típusú formába képez. A Kähler-geometria alapvető azonossága ekkor azt mondja ki, hogy
-típusú formát ugyanilyen típusú formába képez. A Kähler-geometria alapvető azonossága ekkor azt mondja ki, hogy
Ebből és az előző észrevételből azonnal következik, hogy a harmonikus ![]() -formák vektortere felbomlik típus szerint:
-formák vektortere felbomlik típus szerint:
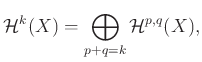
ahol ![]() a tiszta
a tiszta ![]() -típusú harmonikus formák tere. Továbbá, mivel
-típusú harmonikus formák tere. Továbbá, mivel ![]() könnyen láthatóan valós operátor (azaz, kommutál a komplex konjugálással), azért létezik egy
könnyen láthatóan valós operátor (azaz, kommutál a komplex konjugálással), azért létezik egy
izomorfizmus. A fenti fogalmak és eredmények részletesebb kifejtése megtalálható például a [4] tankönyv bevezető fejezetében.
Az előző paragrafusban nyert struktúrát tetszőleges ![]() véges-dimenziós, komplex konjugálással ellátott komplex vektortéren értelmezhetjük: azt mondjuk, hogy
véges-dimenziós, komplex konjugálással ellátott komplex vektortéren értelmezhetjük: azt mondjuk, hogy ![]() -n egy
-n egy
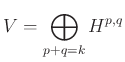
direkt-összeg felbontás megad egy tiszta ![]() -súlyú komplex Hodge-struktúrát, ha minden
-súlyú komplex Hodge-struktúrát, ha minden ![]() párosra teljesül a következő feltétel:
párosra teljesül a következő feltétel:
Ezzel a terminológiával élve tehát Hodge tétele azt mondja ki, hogy a ![]() de Rham kohomológia-téren létezik egy természetes tiszta
de Rham kohomológia-téren létezik egy természetes tiszta ![]() súlyú Hodge-struktúra.
súlyú Hodge-struktúra.
Kanyarodjunk vissza a kiinduló-pontunkhoz: a véges testek feletti algebrai varietások racionális pontjainak kérdéséhez, amelyről 1949-ben A. Weil négy mély tulajdonságot sejtett meg. A Weil-sejtések teljes bizonyítása P. Deligne nevéhez fűződik [1], amely eredményéért 1978-ban Fields-éremmel jutalmazták. Magukat a sejtéseket itt teljes részletességgel nem közöljük, csupán egy azokból következő, első látásra talán meglepő összefüggést egy ![]() algebrai varietás leszámláló-függvénye és az
algebrai varietás leszámláló-függvénye és az ![]() -hez rendelt
-hez rendelt ![]() komplex analitikus sokaság de Rham kohomológia-tereinek dimenziói között.
komplex analitikus sokaság de Rham kohomológia-tereinek dimenziói között.

A tétel feltétele erősnek tűnhet, ám kiderül hogy az így is lefed számos érdekes esetet. Lássunk ezek közül egyet!
Deligne fenti tételének eredménye csak sima projektív varietásokra igaz. A tiszta Hodge-struktúra fogalmának létezik egy kiterjesztése, az úgynevezett kevert Hodge-struktúra, amelynek kidolgozása szintén Deligne érdeme [2], [3]. Bebizonyította többek között, hogy amennyiben ![]() nem sima vagy nem projektív, akkor a de Rham-kohomológia terein kevert Hodge-struktúra értelmezhető. Ennek a kevert Hodge-struktúrának a segítségével pedig bevezethető egy
nem sima vagy nem projektív, akkor a de Rham-kohomológia terein kevert Hodge-struktúra értelmezhető. Ennek a kevert Hodge-struktúrának a segítségével pedig bevezethető egy ![]() kétváltozós polinom. N. Katz általánosította Deligne tételeinek fenti következményét [6]: bebizonyította, hogy ha egy
kétváltozós polinom. N. Katz általánosította Deligne tételeinek fenti következményét [6]: bebizonyította, hogy ha egy ![]() algebrai varietás leszámláló-függvénye valamely
algebrai varietás leszámláló-függvénye valamely ![]() polinom, akkor
polinom, akkor![]()
Ezen további elméletek magyarázata azonban már túlmutat jelen cikkünk keretein.
Szabó Szilárd
BME Matematika Intézet, Geometria Tanszék
Irodalomjegyzék
- 1
- P. Deligne, La conjecture de Weil: I, Publ. Math. IHES, 43, 1974.
- 2
- P. Deligne, Théorie de Hodge. II, Publ. Math. IHES, 40, 1971.
- 3
- P. Deligne, Théorie de Hodge. III, Publ. Math. IHES, 44, 1974.
- 4
- P. Griffiths, J. Harris, Principles of Algebraic Geometry, John Wiley & Sons, 1978.
- 5
- W. Hodge, The Theory and Application of Harmonic Integrals, Cambridge University Press, New York, 1941.
- 6
- N. Katz,
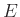 -polynomials, zeta-equivalence and polynomial count varieties, függelék itt: T. Hausel, F. Rodriguez-Villegas, Mixed Hodge polynomials of character varieties, Invent. Math. 174, 2008.
-polynomials, zeta-equivalence and polynomial count varieties, függelék itt: T. Hausel, F. Rodriguez-Villegas, Mixed Hodge polynomials of character varieties, Invent. Math. 174, 2008.
Lábjegyzetek
- 1
- Remélhetőleg, az olvasó nem téveszti össze az itt bevezetett
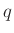 számot a korábban szintén
számot a korábban szintén 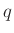 -val jelölt prímhatvánnyal — mivel mindkét jelölés bevett az elméletben, a szerző nem kíván eltérni egyiktől sem.
-val jelölt prímhatvánnyal — mivel mindkét jelölés bevett az elméletben, a szerző nem kíván eltérni egyiktől sem. - 2
- A tétel ennél gyengébb feltételek mellett is igaz, amelyek kimondása azonban itt túl technikai lenne.










 d
d