Egy feladat és ami róla az eszembe jutott...
Az idei Győr–Moson–Sopron Megyei Matematikaverseny egyik feladatát Árki Tamás (Révai Miklós Gimnázium és Kollégium, Győr) kollégám javasolta. A feladat a ![]() háromszögről szólt.
háromszögről szólt. ![]() . Elgondolkodtam. Biztos lesz itt szép megoldás!
. Elgondolkodtam. Biztos lesz itt szép megoldás!
A következőkben 6 megoldást mutatok. Mind a hat a maga nemében szép, vagy valami szép tulajdonságot használ.
A feladat
Az ![]() háromszögben
háromszögben ![]() és
és ![]() . Az
. Az ![]() oldal
oldal ![]() -n túli meghosszabbításán vegyük fel a
-n túli meghosszabbításán vegyük fel a ![]() pontot úgy, hogy
pontot úgy, hogy ![]() teljesüljön. Számítsuk ki az
teljesüljön. Számítsuk ki az ![]() nagyságát.
nagyságát.
1. megoldás
Használjuk fel, hogy a feladatban szereplő szögekre ![]() .
.
Rajzoljuk az ![]() oldalra az
oldalra az ![]() szabályos háromszöget az ábra szerint. Kössük össze a
szabályos háromszöget az ábra szerint. Kössük össze a ![]() és
és ![]() pontokat.
pontokat.
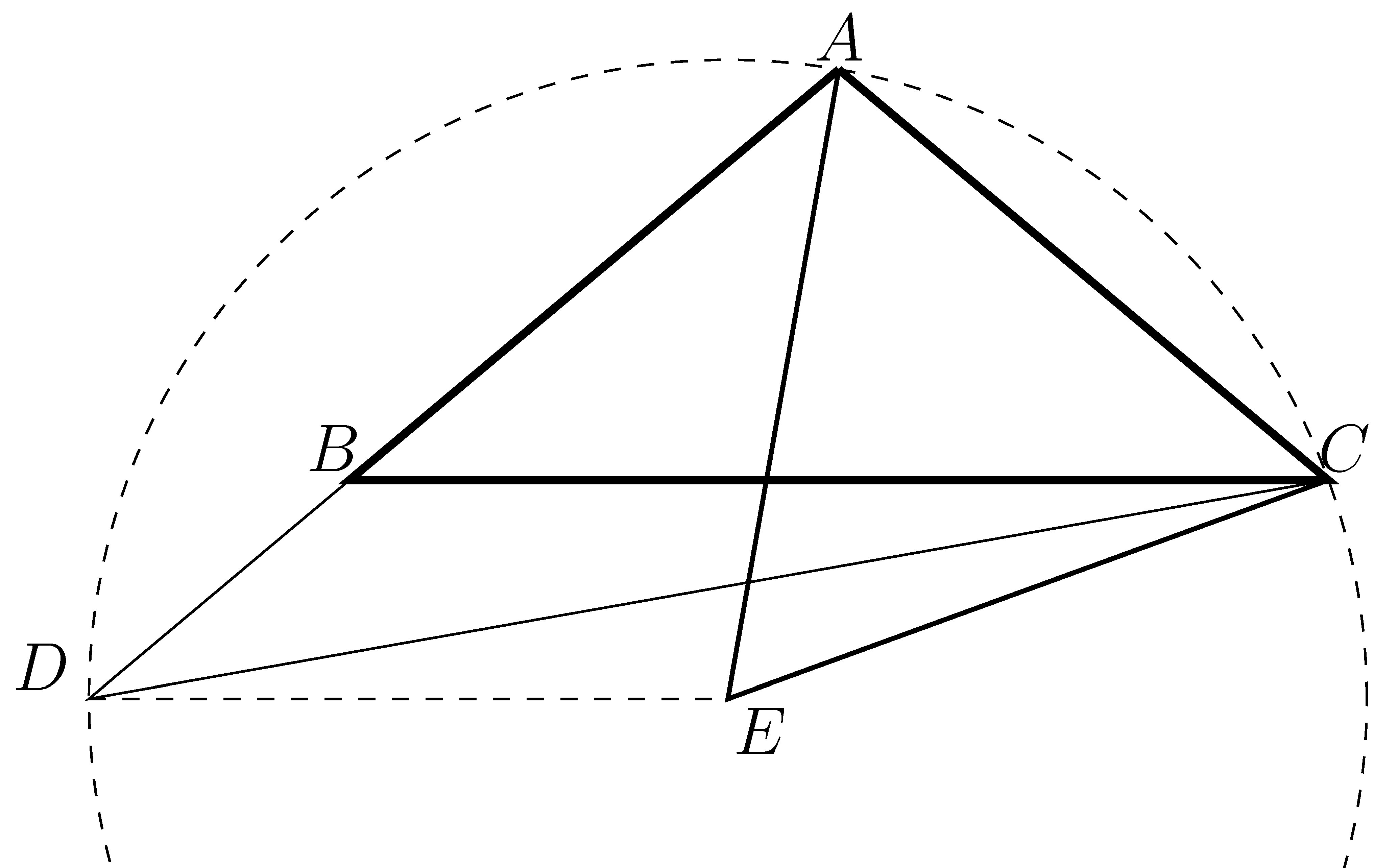
1. ábra
Ezért ![]() , vagyis az
, vagyis az ![]() ,
, ![]() és
és ![]() pontokra illeszkedő kör középpontja
pontokra illeszkedő kör középpontja ![]() . Mivel az
. Mivel az ![]() szakasz
szakasz ![]() -ből
-ből ![]() alatt látszik, a
alatt látszik, a ![]() kerületi pontból
kerületi pontból ![]() alatt. Tehát a keresett szög
alatt. Tehát a keresett szög ![]() -os.
-os.
2. megoldás
Most is felhasználjuk, hogy a feladatban szereplő szögekre ![]() , de máshol keressük ezt a szöget.
, de máshol keressük ezt a szöget.
Rajzoljuk meg a feladatban szereplő ![]() háromszöggel egybevágó
háromszöggel egybevágó ![]() háromszöget az ábrán látható módon úgy, hogy
háromszöget az ábrán látható módon úgy, hogy ![]() legyen. Kössük össze a
legyen. Kössük össze a ![]() és
és ![]() pontokat.
pontokat.
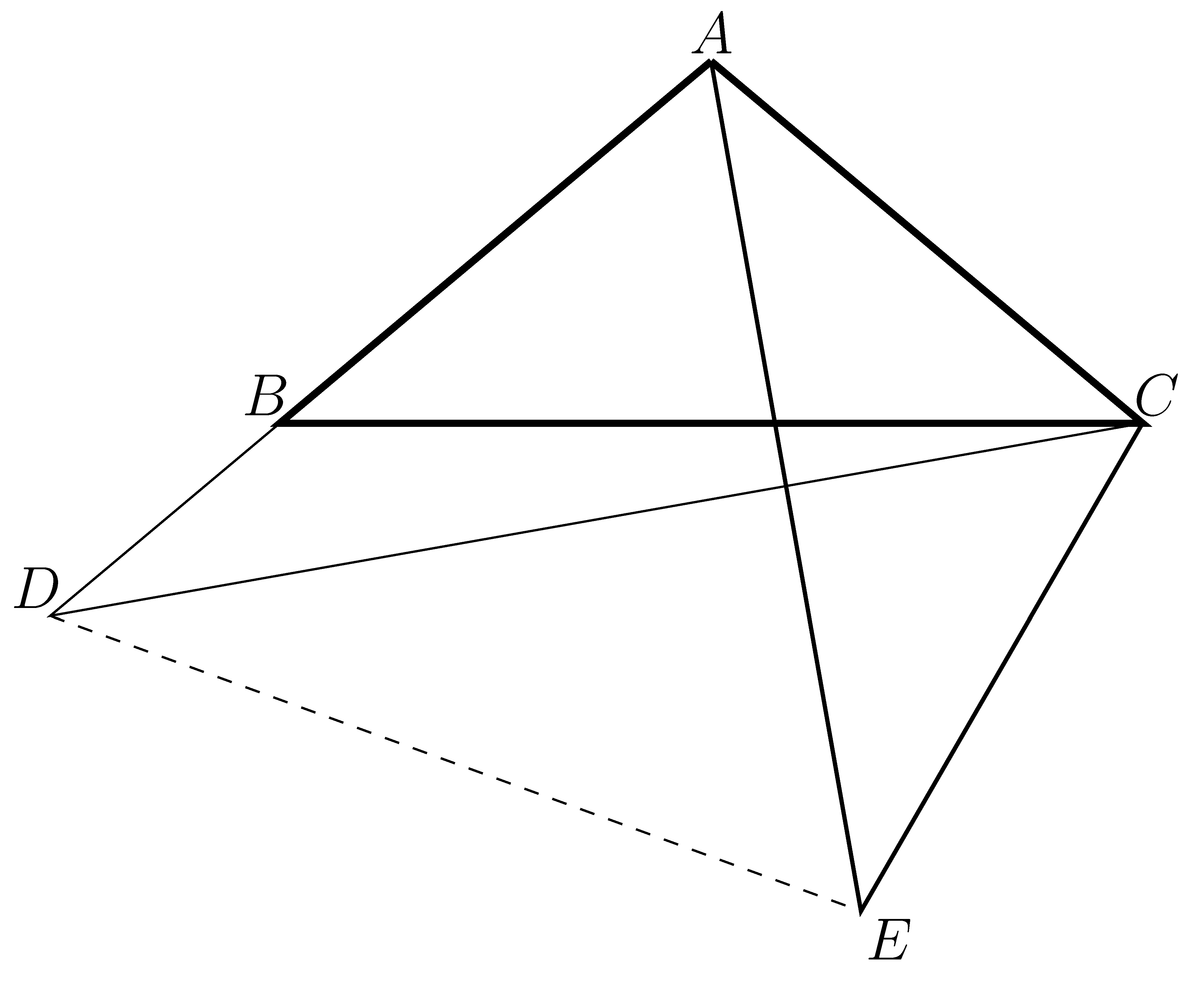
Ekkor és
![]() , valamint
, valamint
tehát a ![]() háromszög szabályos, így
háromszög szabályos, így ![]() is teljesül. Az
is teljesül. Az ![]() négyszög tehát deltoid, (
négyszög tehát deltoid, (![]() és
és ![]() ), amelynek szimmetria átlója a
), amelynek szimmetria átlója a ![]() szakasz, tehát felezi az
szakasz, tehát felezi az ![]() szöget.
szöget.
Ebből következik, hogy a keresett szög 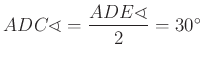 .
.
3. megoldás
Ebben a megoldásban nem a szögek különbségét keressük, hanem a két szög összegét: ![]() .
.
Rajzoljunk ![]() szabályos háromszöget a
szabályos háromszöget a ![]() oldalra az ábra szerint. Kössük össze a
oldalra az ábra szerint. Kössük össze a ![]() és
és ![]() pontokat.
pontokat.
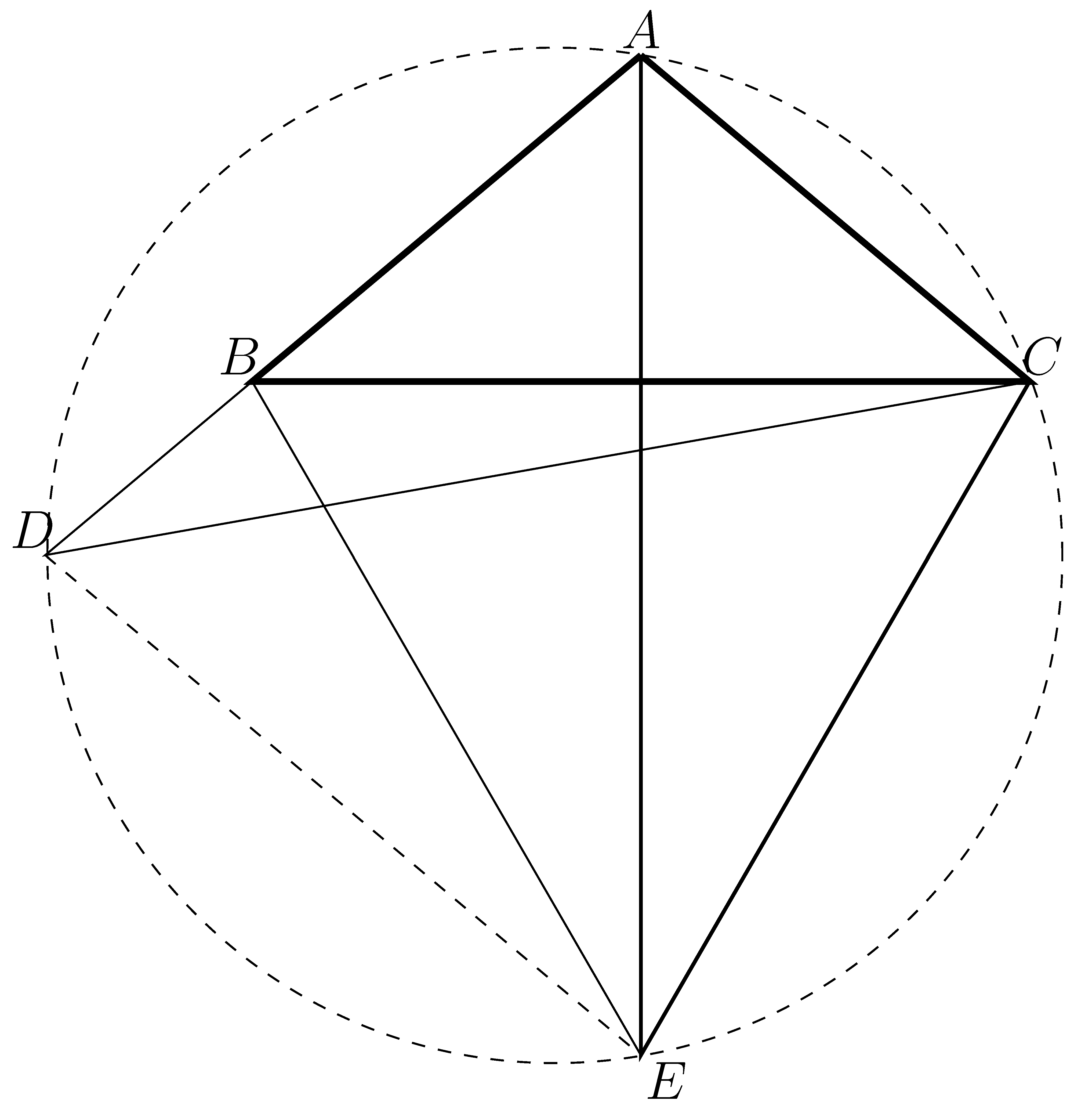
![]() és
és ![]() , tehát az
, tehát az ![]() négyszög deltoid, amelynek
négyszög deltoid, amelynek ![]() szimmetria átlója, így
szimmetria átlója, így 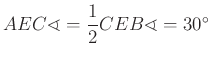 .
.
![]() , azaz
, azaz ![]() , és
, és , így az
![]() négyszög szimmetrikus trapéz, tehát húrnégyszög.
négyszög szimmetrikus trapéz, tehát húrnégyszög.
A négyszög köré írható körben az ![]() szakasz az
szakasz az![]() pontból és a
pontból és a ![]() pontból egyenlő szögben látszik, tehát
pontból egyenlő szögben látszik, tehát .
4. megoldás
Most keressük a szabályos háromszöget egy meglepő helyen.
Rajzoljunk az ![]() oldalra az eredetivel egybevágó
oldalra az eredetivel egybevágó ![]() háromszöget az ábra szerint.
háromszöget az ábra szerint.
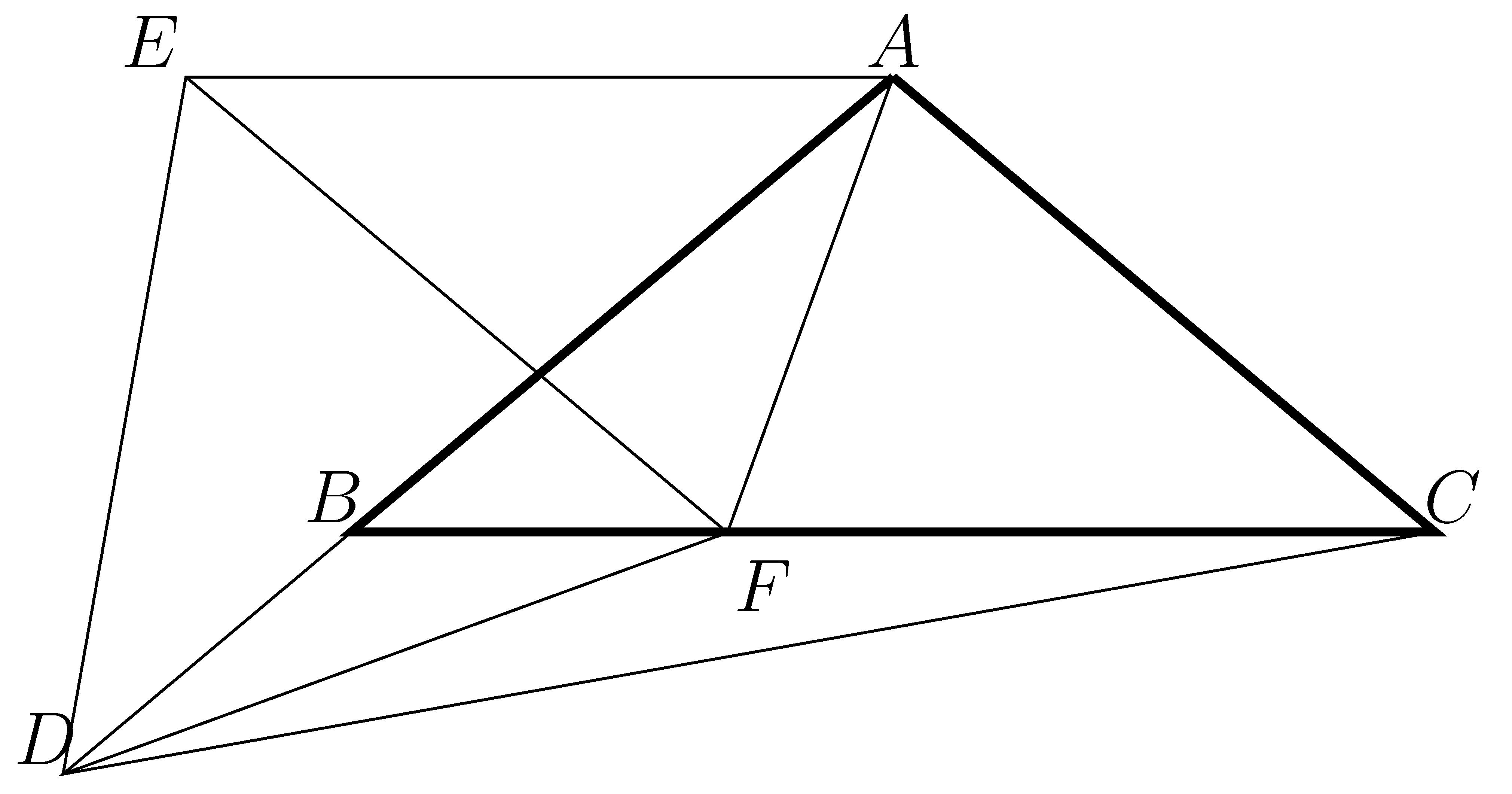
Legyen ![]() a
a ![]() oldalnak azon pontja, amelyre
oldalnak azon pontja, amelyre ![]() . Kössük össze az
. Kössük össze az pontot a
és az
csúcsokkal.
Számítsuk ki az ![]() négyszög szögeit!
négyszög szögeit!
![]() ,
, ![]() , ami azt jelenti, hogy
, ami azt jelenti, hogy ![]() . Mivel
. Mivel ![]() is teljesül, az
is teljesül, az ![]() négyszög rombusz, amelynek szögei
négyszög rombusz, amelynek szögei ![]() és
és ![]() -osak.
-osak.
Tekintsük most az ![]() háromszöget.
háromszöget. ![]() , és mivel
, és mivel ![]() , az
, az ![]() háromszög szabályos, vagyis
háromszög szabályos, vagyis ![]() . Innen
. Innen ![]() .
.
A ![]() háromszög egyenlő szárú, mert
háromszög egyenlő szárú, mert ![]() .
. ![]() , így
, így ![]() . Tehát
. Tehát ![]() .
.
5. megoldás
Most nézzünk egy teljesen más megoldást, amely trigonometriára támaszkodik. A megoldás során felhasználjuk a
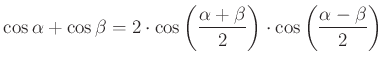
és ennek egy másik formáját, a
azonosságot is.
Vegyük fel ![]() oldal meghosszabbításán azt az
oldal meghosszabbításán azt az ![]() pontot, amelyre
pontot, amelyre ![]() . (Mivel
. (Mivel ![]() , ez az
, ez az ![]() pont létezik.)
pont létezik.)
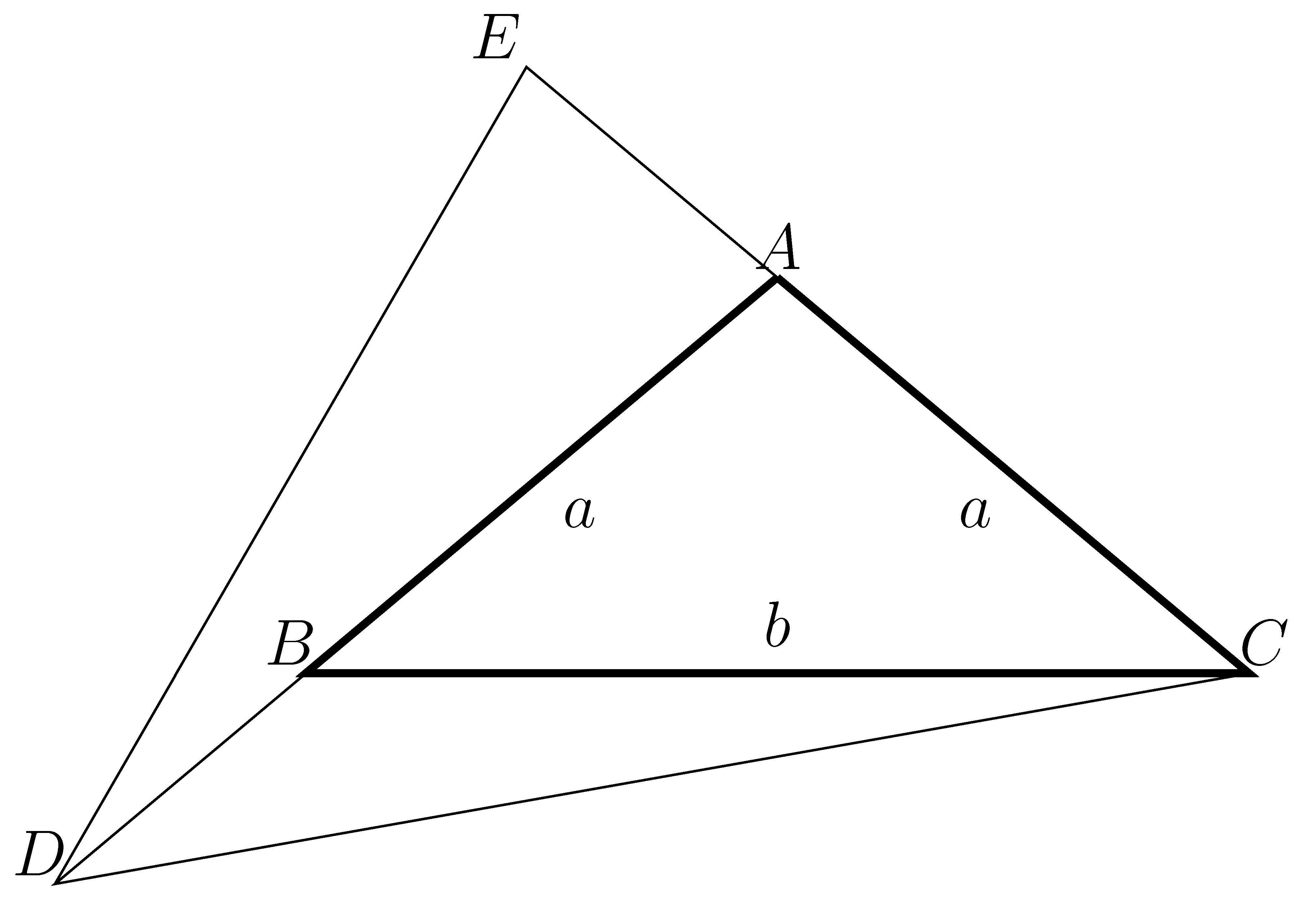
Az ![]() háromszögben a szárak hosszai
háromszögben a szárak hosszai ![]() , válasszuk ezt egységnyinek, azaz
, válasszuk ezt egységnyinek, azaz . Az
![]() -ból induló magasság két olyan derékszögű háromszögre bontja az
-ból induló magasság két olyan derékszögű háromszögre bontja az ![]() háromszöget, amelyekben definíció szerint
háromszöget, amelyekben definíció szerint 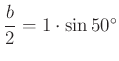 , azaz
, azaz ![]() .
.
Mivel ![]() (hiszen így vettük fel a
(hiszen így vettük fel a ![]() pontot), továbbá
pontot), továbbá ![]() , ebből következik, hogy
, ebből következik, hogy
Mivel

azért
ami azt jelenti, hogy ![]() , azaz a
, azaz a ![]() háromszög egyenlő szárú. Mivel
háromszög egyenlő szárú. Mivel ![]() , ebből következik, hogy
, ebből következik, hogy ![]() .
.
A keresett szög:
6. megoldás
És végül mutatunk egy tisztán trigonometrikus gondolatmenetet. A megoldás során felhasználjuk a
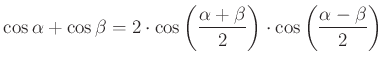
azonosságot.
Legyen az ![]() háromszög szárainak hossza
háromszög szárainak hossza ![]() ; válasszuk ezt egységnyinek, azaz
; válasszuk ezt egységnyinek, azaz . Ekkor az
![]() -ból induló magasság két olyan derékszögű háromszögre bontja a háromszöget, amelyekben definíció szerint
-ból induló magasság két olyan derékszögű háromszögre bontja a háromszöget, amelyekben definíció szerint ![]() , azaz
, azaz ![]() .
.
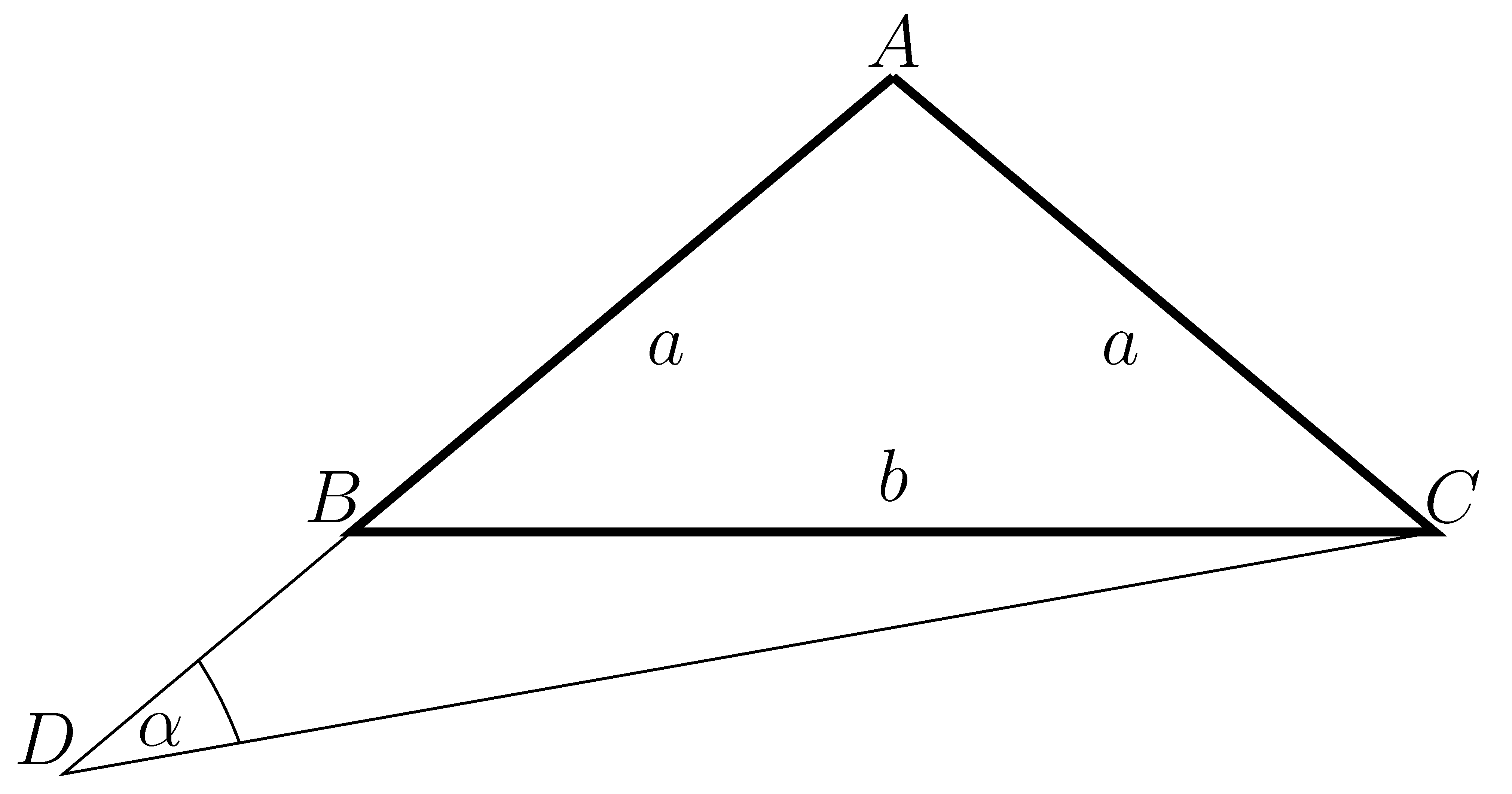
Felírva a szinusztételt az ![]() háromszög
háromszög ![]() és
és ![]() oldalaira (
oldalaira (![]() -val jelölve a keresett
-val jelölve a keresett ![]() szöget)
szöget)
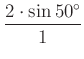 |
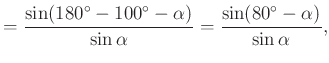 |
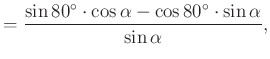 |
|
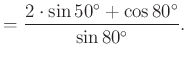 |
A kifejezést tovább alakítva
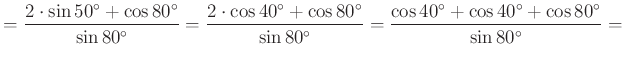 |
|
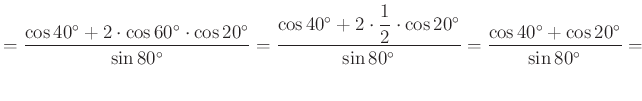 |
|
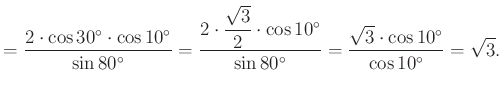 |
Eszerint ![]() , azaz
, azaz ![]() .
.
Zárszó
Kedves Olvasó! Ha egy másik „szép” megoldást talál, kérem küldje el nekem a Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát. e-mail címre. Ezeket az újabb megoldásokat összegyűjtve időnként (terveim szerint) szintén megmutatnám.









