Az agykutatás eredményei alátámasztják, hogy gyerekkorban csak az észleleteket képes mozgósítani az ember, csak a képeket, eljátszott történéseket képes felhasználni gondolkodásában, s nem a hozzá kapcsolódó szavak, nem a róluk szóló mondatok mobilizálódnak. (Vigotszkij pl. így idézi Rimat kutatási következtetését: „….A szemléltető momentumoktól elszakított fogalmakban való gondolkodás olyan követelményeket támaszt a gyerekkel szemben, amelyek tizenkét éves kora előtt pszichológiai lehetőségeit túlhaladják.”[1]) A verbális vagy írott jelekhez először képeket, átélt élményeket kell előhívnia 6–12 éves korában, hogy azzal kezdhessen valamit. Ha hiányzik a kép, akkor a szó nem lesz való semmi értelmi tevékenységre.
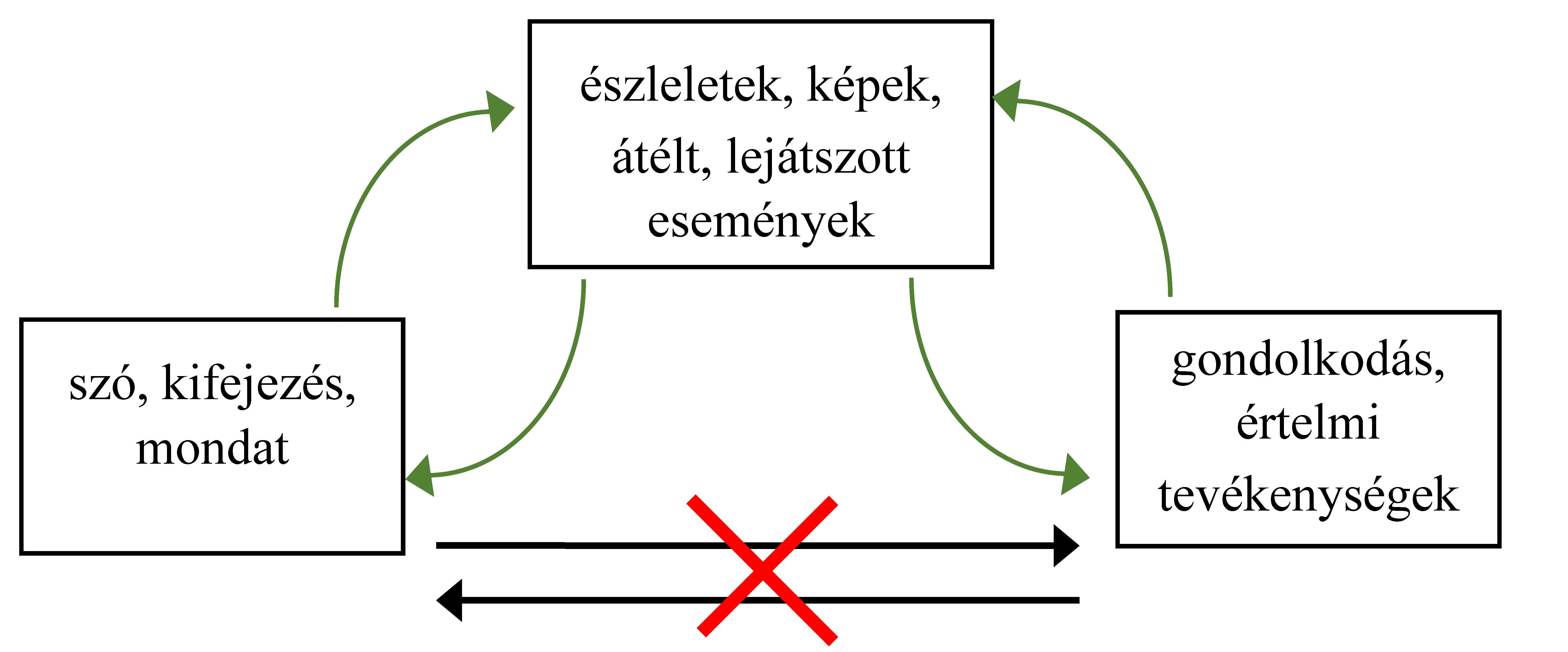Vajon miért hisszük, hogy egy elmondott, leírt és esetleg sokszori ismétléssel „rögzített” állítás, meghatározás azt jelenti egy gyerek (vagy akár egy másik felnőtt) számára, mint annak, aki ezt a szöveget közvetítette? Hiszen egy-egy köznyelvi szó sem ugyanazt idézi fel mindenki számára! Néha eltöprengek rajta (bár már rég nem lep meg), hogy nekem mennyivel mást jelent a szó: „szabadság”, mint unokáimnak, vagy akár a fiamnak. Nem azt élték át, amit én. De kevésbé elvont fogalmakat jelentő szavaink sem pontosan ugyanazt fejezik ki mindenkinek. Sőt, bizonyára két, egymás mellett felnövő ikertestvérnek sem!
Mondhatjuk-e, hogy „viszont a pontosan, jól meghatározott, definiált fogalmak éppen azért képezhetik egy tudomány szilárd vázát, mert azok már mindenkinek ugyanazt jelentik”? Tehát fogalmazzuk meg pontosan a meghatározásainkat, tanulják meg ezeket a növendékeink, és ezzel kiépítettük fejükben egy tudomány hibátlan fogalmi rendszerét?
Hát nem! A meghatározás megértéséhez, azonos értelmezéséhez arra lenne szükség, hogy a definícióban már benne szereplő szavak, a szótövek, és a szavakat összekapcsoló végződések, a szavak sorrendje, mondatrészek viszonya, a mondatok egymáshoz fűzése legyen mindenki számára azonos jelentésű, kialakult értelmű! De mi van akkor, amikor már a meghatározásban szereplő többi szóval jelzett fogalom is üres, vagy éppen más-más háttérbeli élmények alapján más-más tartalmat hordoz? És ha a végződések jelentése bizonytalan? Ha egy-egy szó – pl. a határozott névelő – szerepeltetése, vagy elhagyása fel sem tűnik? Ha a szórendcsere csak formai, s nem jelentésbeli változást mutat valakinek?
Kalmár László, az elmúlt század egyik legnagyobb matematikusa mondta egyszer: „A gyerek előbb megszületik, aztán adunk neki nevet. Ugyanígy a fogalomnak is előbb kell megszületnie, ráérünk aztán megnevezni.”
De hát akkor hogyan születik meg a fogalom, ha nem mondjuk meg, mit kell érteni rajta?
Most mintaként csak egy fogalomkör épülésével foglalkozom.
Ötödik osztályban egy tehetséges, jó szemléletű tanítójelölt tartotta az órát, aki 5-6. osztályos matematikatanításra is képesítést fog szerezni. A szög fogalmának „kialakítása” volt az óra kijelölt feladata. (Nem véletlenül használom idézőjelben a fogalommal kapcsolatban a „kialakítása” szót!)
Kedves ötlettel indult az óra: a gyerekek kis csoportokban összegyűjtöttek egy egész sor dolgot, ami a „szög” szóról eszükbe jutott. Voltak, akik a technika tanárjukat, a műhelyt, a kalapácsot is felidézték, volt, aki a vas, a szúr, a hegyes jellemzőket gyűjtötte, néhányan a matematikával is kapcsolatba hozták a szót, derékszöget, háromszöget, négyszöget emlegettek.
A „célmegjelölés” után a tanár felrajzolt egy fekvő vonaldarabot a vonalzója mentén, és megkérdezte:
– „Mi ez?”
A választ egyhangúlag mondták ki a gyerekek: egyenes.
– „Igen, egyenes – hagyta jóvá a tanító – de ez még folytatódik erre is és erre is még nagyon sokáig – mutatta. – Ha itt (nagyjából a vonaldarab közepére tett jelet) kijelölünk egy pontot, ezzel kettévágjuk az egyenest, és így két félegyenest kapunk.”
A félegyenes szóhoz tevékenységet is kapcsolt: minden gyerek az alkarjával jelenített meg egy-egy félegyenest, és a tanár utasításai szerint kellett a padszomszédjával a két „félegyenest” különféle helyzetekbe hoznia: „Legyenek merőlegesek egymásra!” „Metsszék egymást!” „Legyenek kitérők!” … Örömmel, és – úgy tűnt – a szavakat értve hajtották végre a teendőket.
Ismét közlés következett:
– „Ha egy pontból húzok két félegyenest – rajzolta –, akkor a két félegyenes a síkot két szögtartományra osztja. De e két félegyenes két szöget is kijelöl: – mutatja a kisebb és a nagyobb szöget (ugyanazon az ábrán) –, ezért ívvel szoktuk megjelölni, hogy melyikről beszélünk éppen,
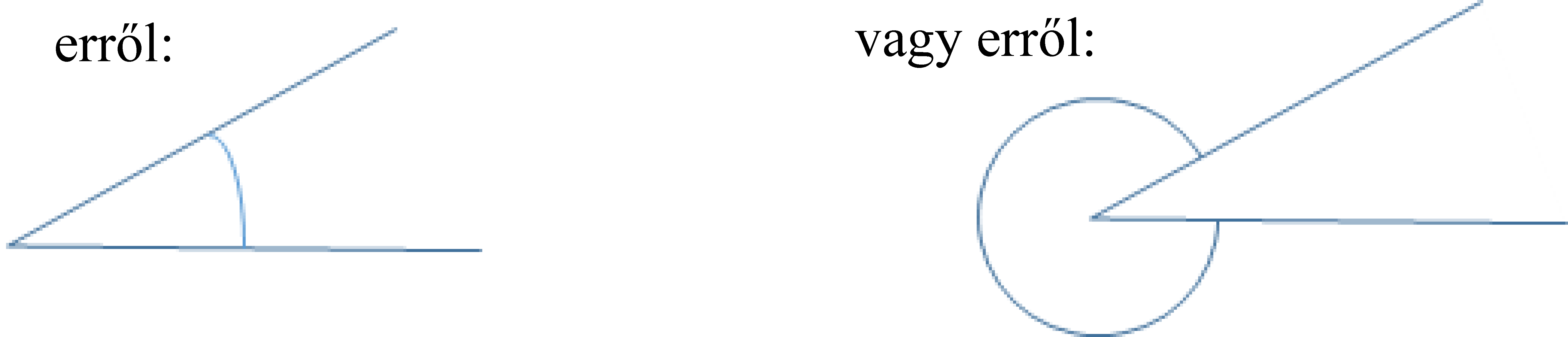
A szög „részeinek” elnevezése során a megfelelő szavakat előbb a táblai ábrán szókártyákon helyezték el a gyerekek, aztán beírták a saját füzetükbe másolt rajz mellé is:
Az óra következő részében a különböző szögfajtákat definiálta a tanárjelölt.
Hasznos szervezési ötlet volt, hogy a gyerekeknek a különféle méretű szögeket ábrázoló, a nekik személyenként kiosztott lapocskákat kellett a mondott meghatározáshoz kiválasztaniuk, majd a megfelelő szakszóhoz társítaniuk. (Ezeket az összepárosításokat ellenőrzésként utóbb a táblán is elvégezték.)
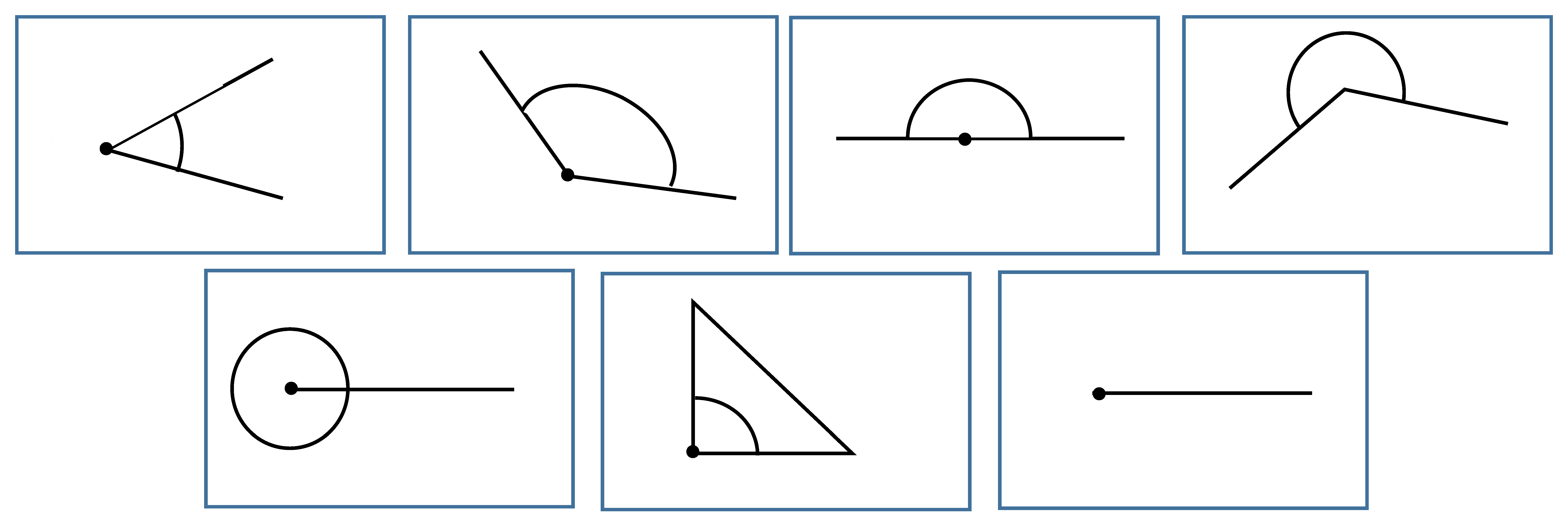
Ilyen meghatározások hangzottak el:
– „Ha a két szögszár merőleges egymásra, akkor az így keletkező két szög közül a kisebbet derékszögnek nevezzük.”
– „Ha a két szögszár egy egyenest alkot, akkor az így keletkező mindkét szöget egyenesszögnek nevezzük.”
– „Ha a két szögszár illeszkedik egymásra, akkor a nagyobb szöget teljes szögnek, a kisebbet nullszögnek nevezzük.”
… Hasonlóan pontos definíciók következtek a hegyesszögre, tompaszögre, és végül a homorúszögre:
– „Az egyenesszögnél nagyobb, de a teljes szögnél kisebb szög a homorú szög.”
A gyerekek rendre megtalálták a meghatározásnak megfelelő ábrákat, és bizonyára megpróbálták a szakszavakat is memorizálni.
Egy néhány órával korábban tanult fogalom is előkerült. A tanítójelölt kijelentette, hogy a homorúszög konkáv, az összes többi konvex. És kérte, bizonyítsák be, hogy a homorú szög valóban konkáv.
Akkor figyelt föl arra, hogy valami nem egészen tiszta a gyerekek számára, amikor a bizonyítás elkezdéséhez a szöget jelölő íven kívül vett fel két pontot a szögtartományban:
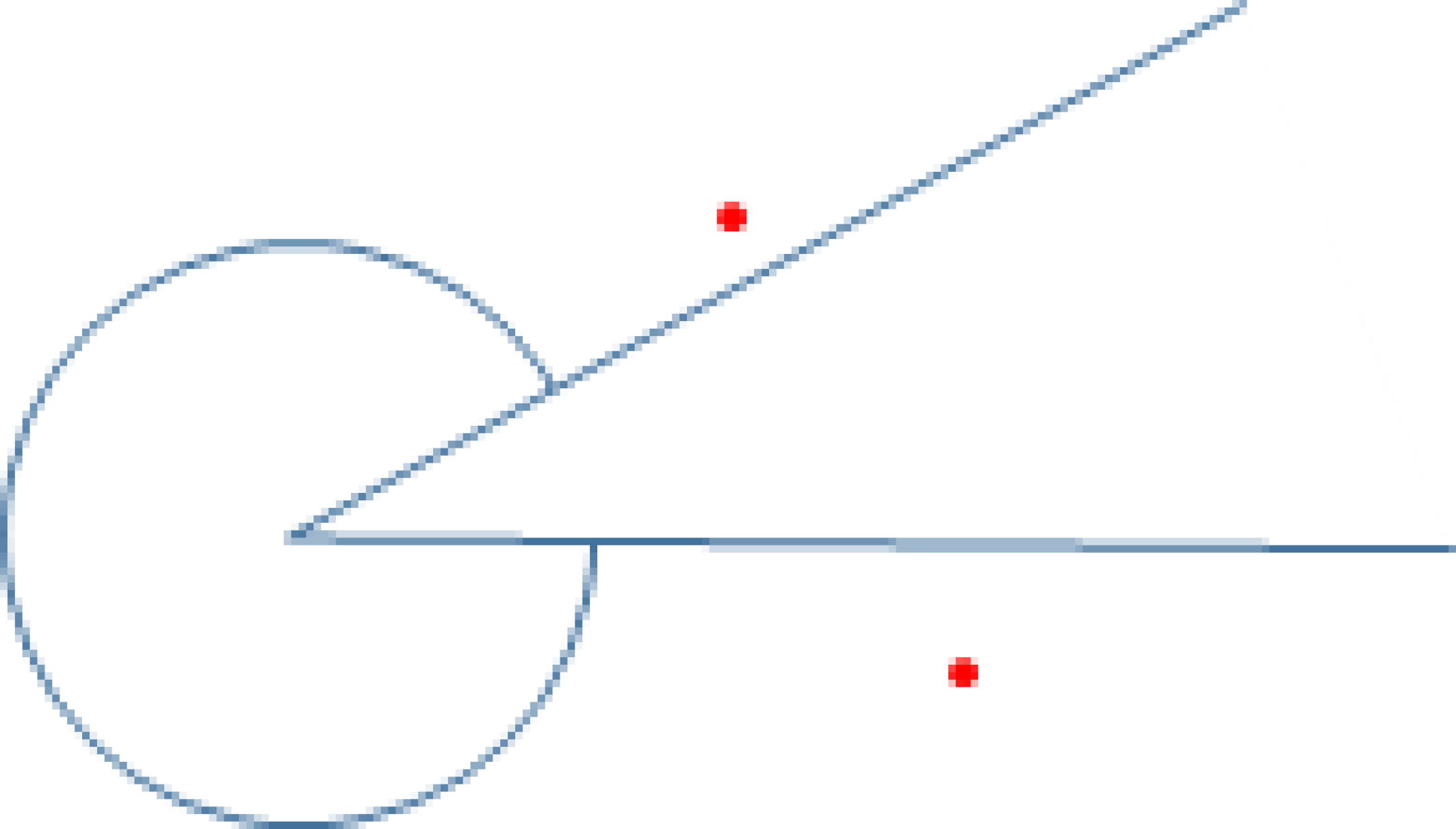
A jelentkező tanuló ugyan mondta, hogy a két pontot összekötő szakasz egy része nem tartozik hozzá a szöghöz, de a levegőben maradt az elbizonytalanodás: „ de hát a két pont sincs benne!”
Vajon a konkáv szó jelentését egészen megértették a gyerekek, amikor a definíciót megtanították nekik? Azt, hogy az alakzatnak van olyan két pontja, amelyek összekötő szakaszának nem minden pontja tartozik az alakzathoz. A halmazokat jellemző kvantorok („mindegyik”, „nem mind”, „van köztük olyan”…) értelmezése egyáltalán nem olyan egyszerű ebben a korosztályban! A gyerekek arcát figyelve nem merném állítani, hogy mindenki tudta, miről is van most szó!
Ami viszont egészen biztosan nem tisztulhatott le a 10–11 éves gyerekek számára, az éppen a szög fogalma. Persze nem csoda, hogy 45 perc alatt nem születik meg egy fogalom. Főképpen azt nem hihetjük, hogy minden gyerek ugyanakkor, ugyanabban a helyzetben, ugyanattól a magyarázattól meg tudja alkotni a fogalmat. Hiszen a fogalom minden ember fejében a saját gondolati tevékenysége során születik! Nem a tanár, vagy más külső személy alakítja ki a gyerekben! Ki-ki a saját „agykohójában” a benne már meglevő alapanyagokból, a benne már működő gondolati tevékenységekkel hozza létre. Ha nincs elegendő és jó alapanyag, vagy esetleg hibásan illeszkednek össze, netán a gondolati tevékenységek nem jól, vagy egyáltalán nem működnek, akkor nem születik meg a fogalom az ő számára, tartalom nélkül marad a szó, vagy éppen hibás tartalom kapcsolódik a kifejezéshez, meghatározáshoz.
Mi is történt a tanulókkal itt az órán?
Találkoztak egy szóval, ami ismerősnek tűnhetett számukra. Ismerős lehetett a „félegyenes” összetett szó, mert a két részét külön-külön legalább már hallották. Ez után egy állítás következett azért, hogy „pontos” tartalmat nyerjen a szó. De az állításban előforduló többi szó értelme sem volt mind tiszta, pontos, tartalmas – hogyan segíthették volna ezek az új fogalom megépítését?
Nem lehetett meg az „egyenes” geometriai fogalma. A gyerekek általában mindössze a „görbeséggel” ellentétes tulajdonságként értik a szót. A „fél” kötődhet egy viszonyított mennyiséghez, (fél kiló, fél méter, fél liter…), de jelölhet valamilyen alakzatot is. (Most vajon melyik tartalom jelenik meg a gyerek fejében?) És a „sík” jelentése, fogalmi tartalma is labilis, kialakulatlan még ebben az életkorban. Hiszen mind az egyenes, mind a sík fogalmához elengedhetetlenül hozzátartozik a „végtelenség”. Ennek megragadására pedig szintén nincs felkészülve a 10-12 éves kisgyerek. (20 év körüli egyetemi hallgatók körében is találkoztam a fogalom bizonytalanságával!)
És vajon a gondolati tevékenységek olyan szinten vannak-e már, amelyek az esetleg valóban kialakult fogalmakból újakat tudnak létrehozni ezek a kisgyerekek? Képesek-e osztályozni, rendezni elvont szinten? Oksági kapcsolatokat megragadni? Valószínűleg a jó tanítók már sokat tettek ennek érdekében, de tapasztalhatjuk, hogy még a 8-9. osztályos tanulók is csak tárgyi tevékenység elvégzése (vagy legalább felidézése) mellett képesek „rendet tenni” különféle fogalmak körében.
De ha ennyire a gyerek meglévő munícióján és kompetenciáin múlik, hogy megszülethessen a fejében egy fogalom, akkor mit tehetünk mi érte?
Természetesen nagyon sokat. Csak nem kell azt hinnünk, hogy a mi szavaink, állításaink hozzák létre az elvont fogalmakat. A definiálás helyett sokszínű szemléleti és hiánytalan tartalmi változatosságban[2] kell biztosítanunk a gondolati alapanyag megszerzéséhez szükséges tapasztalati élményeket! Szerveznünk kell elegendő, saját tárgyi tevékenységet, amellyel mindenki kivetítheti maga elé, ezáltal megértheti, elsajátíthatja a gondolati tevékenységeket: az általánosítást, specializálást, osztályozást, alá- és fölérendelést, rendezést. Érdekes, izgalmas problémafelvetésekkel segíthetjük beindítani a gondolati motort: a belső motiváltságot.
A „szög” egyáltalán nem egységes fogalom[3]. Gyakran ezt a meghatározást használjuk:
– „A szög (szögtartomány) két, közös kezdőpontú félegyenes által határolt síkrész.” (Ennek más megfogalmazása hangzott el az idézett órán.)
Tehát ebben az értelemben a szög egy alakzat, ponthalmaz. A sík azon pontjai alkotják, amelyek a félegyenesek valamelyikén, vagy a félegyenesek „között” vannak. (Persze a homorúszögnél ez a „között” szó is nagyon nem köznapi értelmet rejt!)
– „Más tartalmat fed az a szögfogalom, amely valamilyen módon a szögtartomány nagyságát jellemzi. Eszerint a szög egy mennyiség, amely a félegyenesek által határolt síkrész nagyságával vannak kapcsolatban. (Pl. a „derékszög” szó már legtöbbször nem egy ponthalmazt, síkbeli tartományt jelez, hanem egy méretre utal.)
Az idézett két tartalom olyan viszonyban van egymással, mint a „szakasz” (ami egy egyenesnek két adott pontja által határolt része, azaz ponthalmaz), és a „hosszúság” (amely pl. egy szakasz nagyságát jellemző mennyiség). Ebben az esetben „szerencsénk van”: nem ugyanazzal a szóval adjuk meg a két fogalmat. A szöggel kapcsolatban azonban nem segít a szavakkal való megkülönböztetés.
Ezeket a fogalmi tartalmakat sok matematika feladat összemossa; általában nem tisztázzuk, hogy mely értelemben szerepel bennük a szó. Legtöbbször – számításos feladatokban – a mennyiségről gondolkodunk, bár a meghatározásban a szögtartományt adtuk meg. (Sok esetben „szöget” mondanak a gyerekek, pedig a sokszög csúcsaira gondolnak.) A görög ábécé betűivel magát a szögeket (a tartományt) nevezzük el, de kimondjuk, leírjuk, hogy b = 60o. A magyarázkodás, szavakban való megkülönböztetés előtt azonban először azt kell észrevennünk, hogy mi okozza az értelmezés legfőbb nehézségét a kisgyerek számára.
Úgy vélem, hogy az elmondott meghatározás megértését akadályozó egyik tényező a végtelenség gondolatának kialakulatlansága!
Nem elég azt jelezni, hogy az „egyenes” még nagyon sokáig tart erre és arra is. Akinek egy kis szakasz látványa az „egyenes” szót juttatja az eszébe, az bizonyosan csak a „nem görbe” tulajdonságot látja benne. A „nagyon sokáig” szavak pedig éppen valami – bár távoli – véget is jelezhetnek.
Nagyon nehéz „közel hozni” a gyerekhez a végtelenséget. Mégis elkezdhetjük megmozgatni a képzeletüket. „Az úton soha nem állunk meg, hanem mindig lépünk még egyet, még egyet, még egyet…” „Nem tudsz olyan nagy számot mondani, aminél nagyobbat én ne tudnék választani… +1” „A varázspálcát megfogja a varázsló, és a pálca elkezd nyúlni, nyúlni, nyúlni… és mindig tovább nyúlik, soha nem marad abba a növekedése.” Vagy a félegyenes elképzeléséhez csak az egyik irányba nyúlik, soha nem hagyva abba a növekedést. (A térbeli végtelenséghez így az időbeli végtelenséget próbáljuk segítségként hozzáilleszteni, de talán támogathatják egymást ezek a gondolatok.)
A „végtelenség” megértése nem lenne még elengedhetetlen, ha a szögfogalom mennyiségtartalmának kidolgozását vennénk előbbre. Ahhoz nem szükséges látni a végtelen félegyeneseket, a végtelen síktartományt, hanem egy véges, összehasonlítható, másolható, számokkal jól megadható mennyiségfogalom formálódna. És csak később kerülne sor az egyébként a mindennapokban kevésbé használt „szögtartomány” fogalom alakítására is.
De térjünk vissza a látott óra elképzelt folytatására!
Amikor a gyerekek a karjukkal „szemléltették maguknak" a félegyenest, a kezükbe vehettek volna gondolatban egy „végenincs” hosszú varázspálcát, és tekintetükkel követhették volna iránya szerint a félegyenes végtelenségét.
A szög fogalmának alapozását érdemes valódi mozgásos megtapasztalásból indítani. És ez a tevékenység egyben a szögtartomány nagyságának megtapasztalását is lehetővé teszi.
Ha ezt a „végenincs” félegyenest maguk előtt kinyújtva fordulhatnak a gyerekek pl. egy jobbra-átot végezve, képzeletben átélhetik a derékszögnyi szögtartomány végigsimítását, végigsöprését.
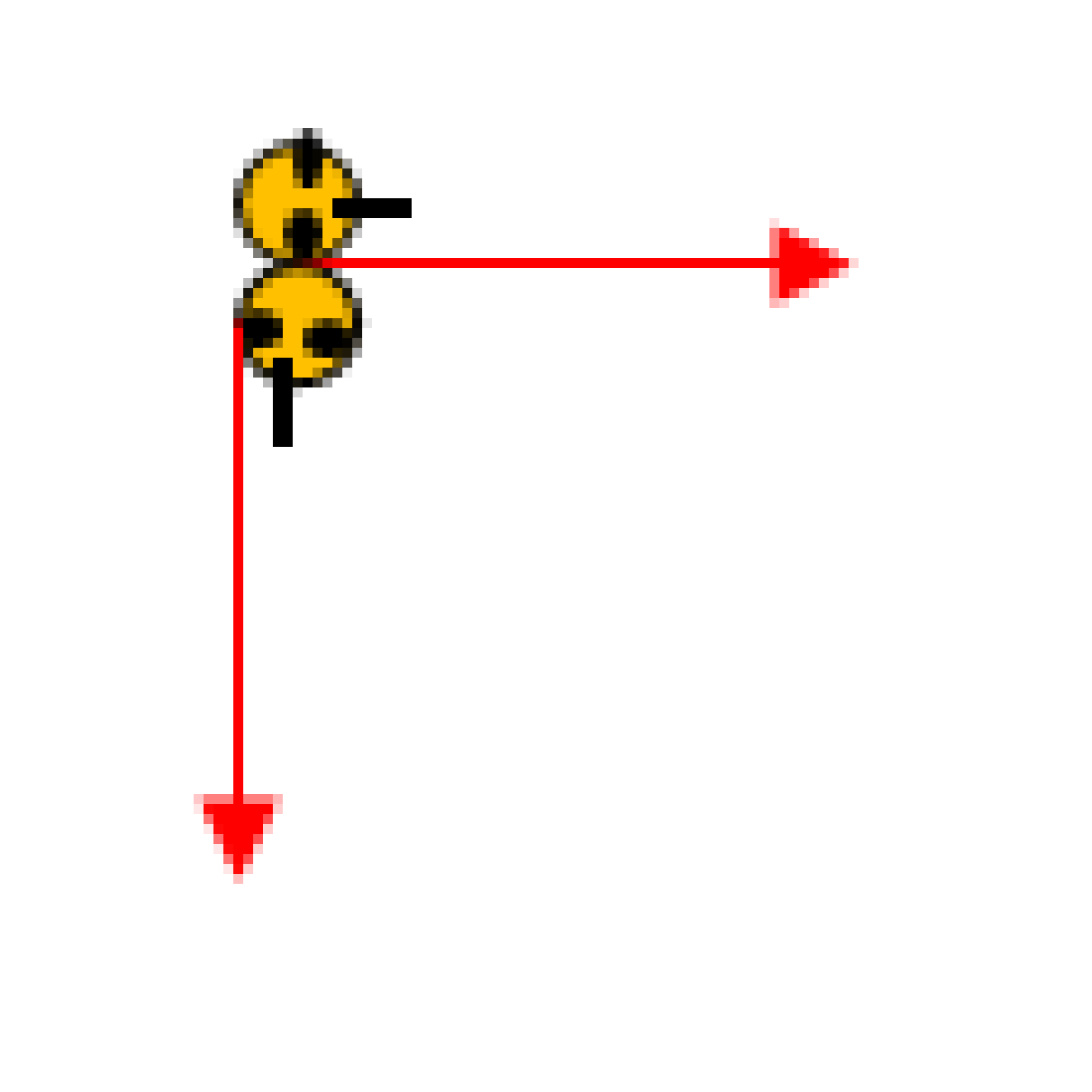
Ha ugyanígy hátraarcot végeznek, a „félszöget” súrolja végig a markukból induló félegyenes.
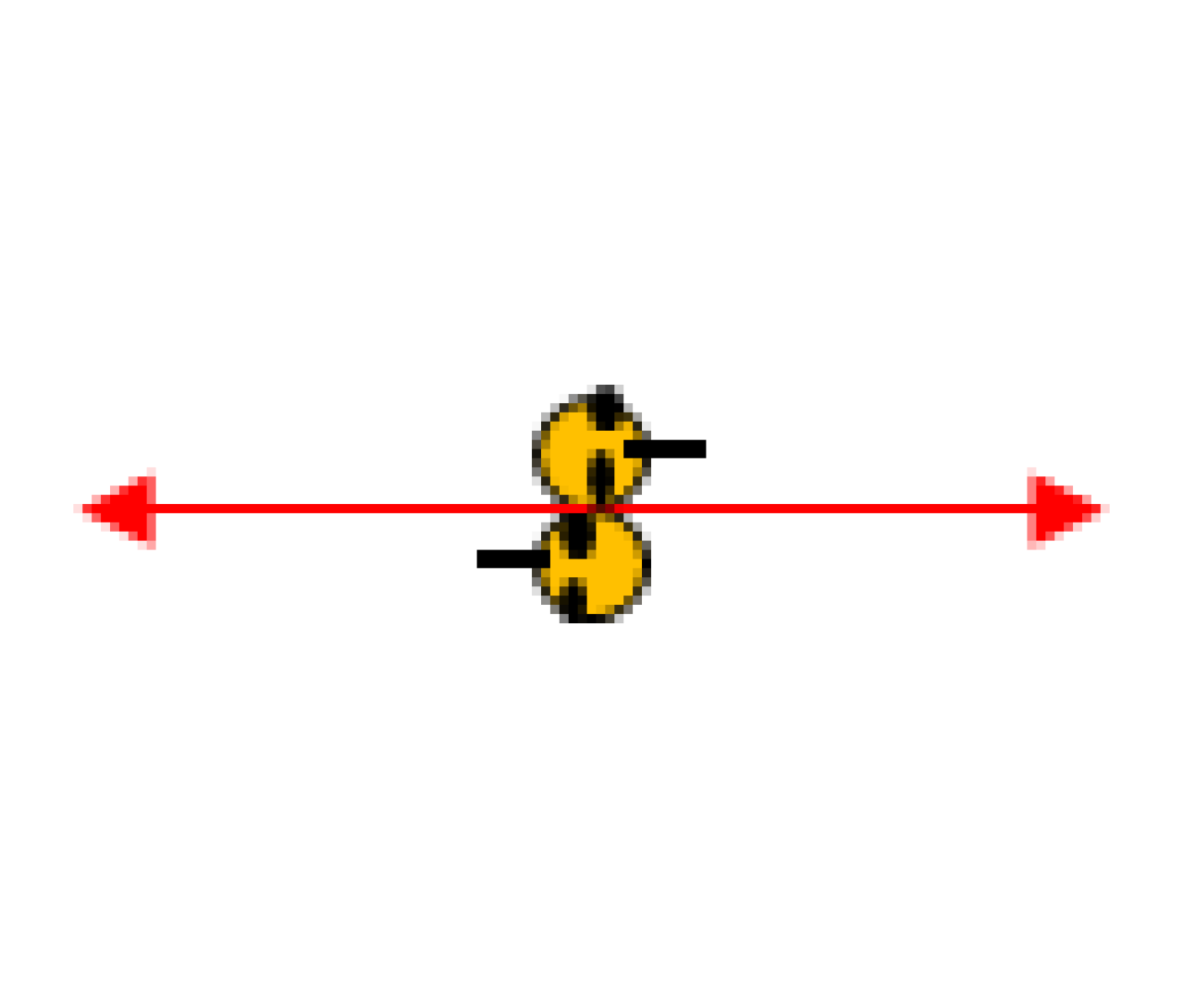
Ellenkező irányban is fordulhatnak, és próbálhatnak pl. egy kb. fél-derékszögnyit elfordulni.
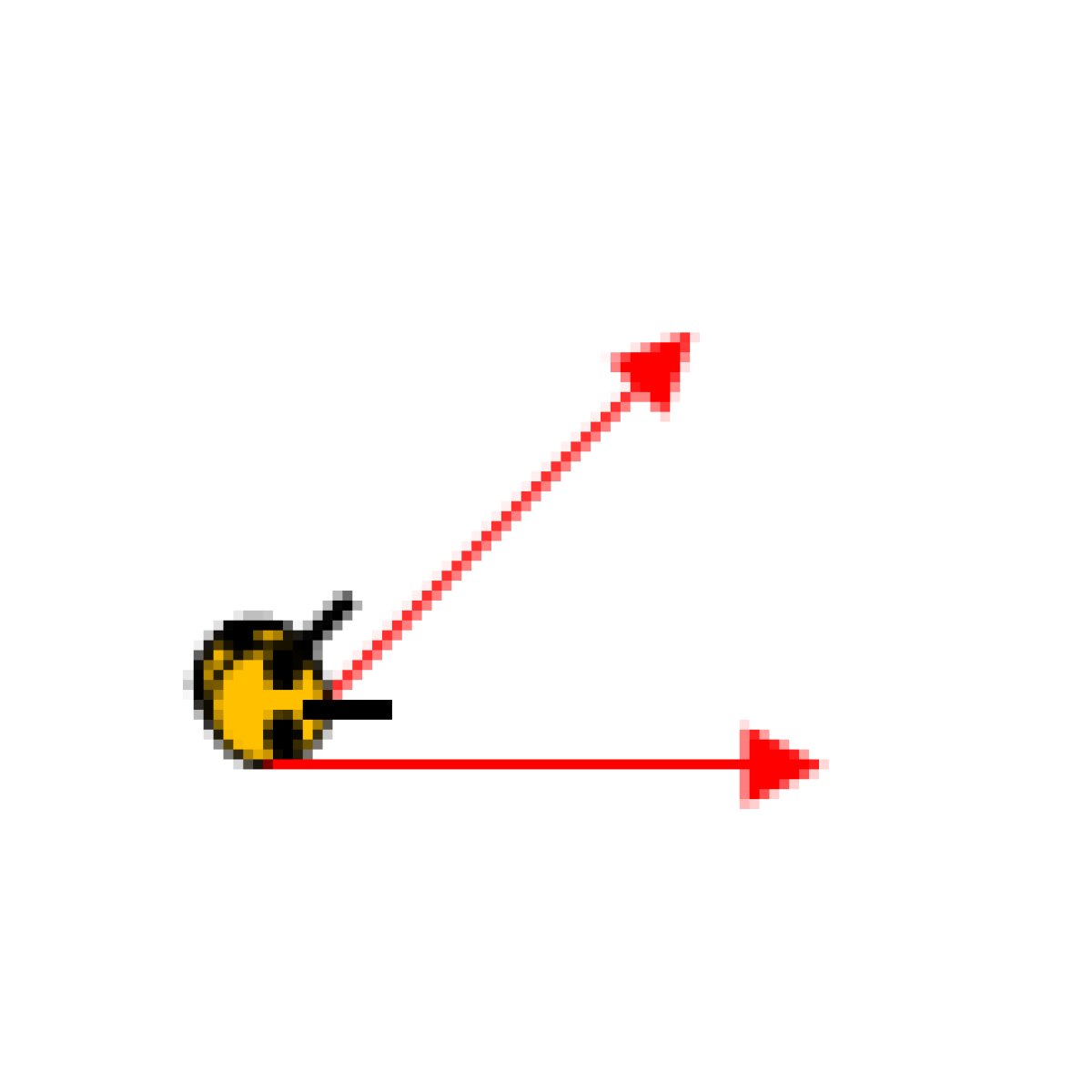
Másolhatnak szögeket földre rajzolt szög csúcsába állva saját elfordulásukkal, és összehasonlíthatják ilyen szögek nagyságát. Maguk előtt forgathatnak bábút a rajzolt szög csúcsába állítva: a bábú orra mutassa a szög egyik szárától a másik szár irányába való fordulást.
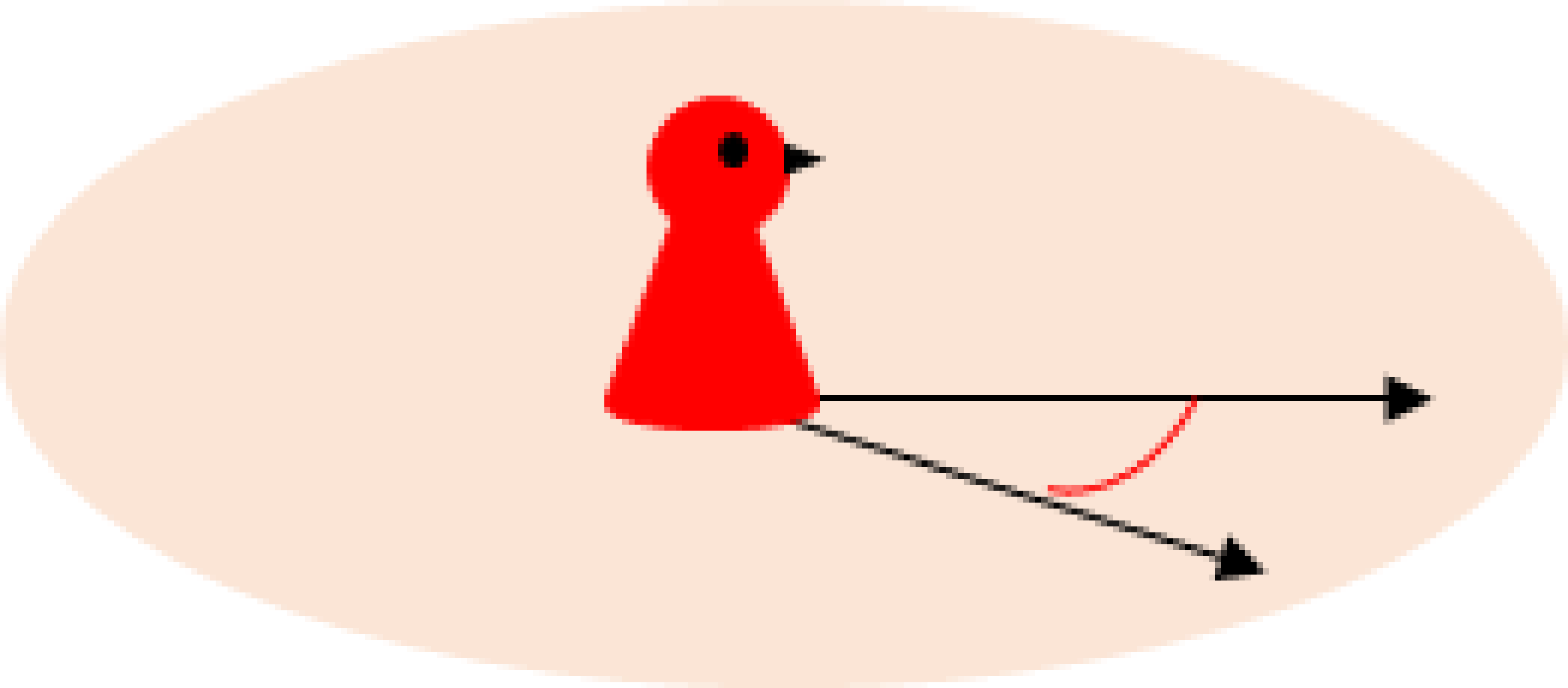
Ahogyan az utat a haladó mozgással élik meg a gyerekek „ponthalmaz-mivoltában”, és az út hosszúságát is mint fizikai mennyiséget, ugyanúgy a forgó mozgás, elfordulás valóságos élménye alapozhatja meg a szögfogalmat szögtartományként és annak méreteként együtt.
Ez az élmény hiányzott az ötletes, szépen megtervezett és gondosan szervezett órából, (ami még a megismert szögfajtákat jelölő szavak gyakorlásával folytatódott).
Az a szerencse, hogy a tanulás folyamata megengedi a pótlást, az elmaradt élmények utólagos kapcsolását. Néha évek múltán értünk meg igazán egy régóta használt fogalmat. De a pedagógus felelőssége, hogy lehetőleg ne bízza a véletlenre: találkoznak-e a növendékei a legfontosabb fogalmak felépítéséhez szükséges elegendő tapasztalati élménnyel!
Lábjegyzetek
[1] Vigotszkij: Gondolkodás és beszéd 2000, Budapest, Trezor Kiadó, 138. old.
[2] Dienes Zoltán: Építsük fel a matematikát!; 1999. Budapest; SHL Hungary Kft.
[3] Varga Tamás pl. 6-féle értelemben is megadja a szakszó meghatározását. L. Varga Tamás: Matematika lexikon Budapest, 2001, Műszaki Könyvkiadó
C. Neményi Eszter