„A matematikai intuíció lángja éppen hogy pislákol a gyermek agyában. Meg kell erősıteni és fenn kell tartani, hogy fénye minden számtani tevékenységre rávetülhessen.'' (Stanislas Dehaene)
Az itt következő írással néhány példán keresztül azt szeretném megmutatni, hogy ha egy geometriai sorozatot végtelen sorozattá terjesztünk ki, akkor ezzel a látszólag kis lépéssel nagymértékben tágíthatjuk diákjaink matematikai szemléletét. Ez a kiterjesztés az első lépés lehet a határérték fogalma felé és megadhatja azt az élményt, amit a végtelen kicsi és a végtelen nagy világa nyújt a megszokott makrovilágunkkal szemben.
Bevezetőül, vizuális képet fogunk adni a véges geometriai sorozat
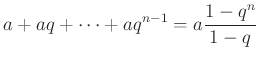 |
(1) |
összegképletére és az (1) összefüggés szokásos bizonyítására.
Az (1) egyenlőségből rögtön következik a végtelen geometriai sorozat összege:
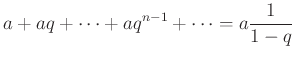 |
(2) |
ha ![]() , amennyiben intuitíve értelmezzük egy végtelen sorozat összegét és elfogadjuk, hogy
, amennyiben intuitíve értelmezzük egy végtelen sorozat összegét és elfogadjuk, hogy ![]() ha
ha ![]()
Geometriai szerkesztéseket fogunk bemutatni (1) és (2) szemléltetésére, amit geometriai modellnek fogunk nevezni. A geometriai modellek vezetnek majd el a ![]() és a (2) formula pontos értelmezésére és az (1) és (2) formulák bizonyıtására.
és a (2) formula pontos értelmezésére és az (1) és (2) formulák bizonyıtására.
Geometriai modell
1. ábra
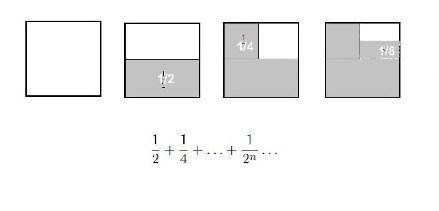
Az 1. ábrán láthatjuk a legegyszerűbb modellt. Itt ![]() és a sorozat első eleme a négyzet területének a fele. Az ábrából úgy tűnik, hogy a végtelen sorozat összege a négyzet
és a sorozat első eleme a négyzet területének a fele. Az ábrából úgy tűnik, hogy a végtelen sorozat összege a négyzet ![]() területe. Ezt abból következtetjük, hogy a szerkesztés minden lépése után a még fehéren maradó rész fele akkora lesz. A matematika nyelvén ezt kifejezve: az
területe. Ezt abból következtetjük, hogy a szerkesztés minden lépése után a még fehéren maradó rész fele akkora lesz. A matematika nyelvén ezt kifejezve: az ![]() -edik lépés után a még fehéren maradó rész területe
-edik lépés után a még fehéren maradó rész területe ![]() .
.
Egy geometriai sorozat részletösszegeinek összetettebb ábrázolását láthatjuk a 2.a. ábrán.
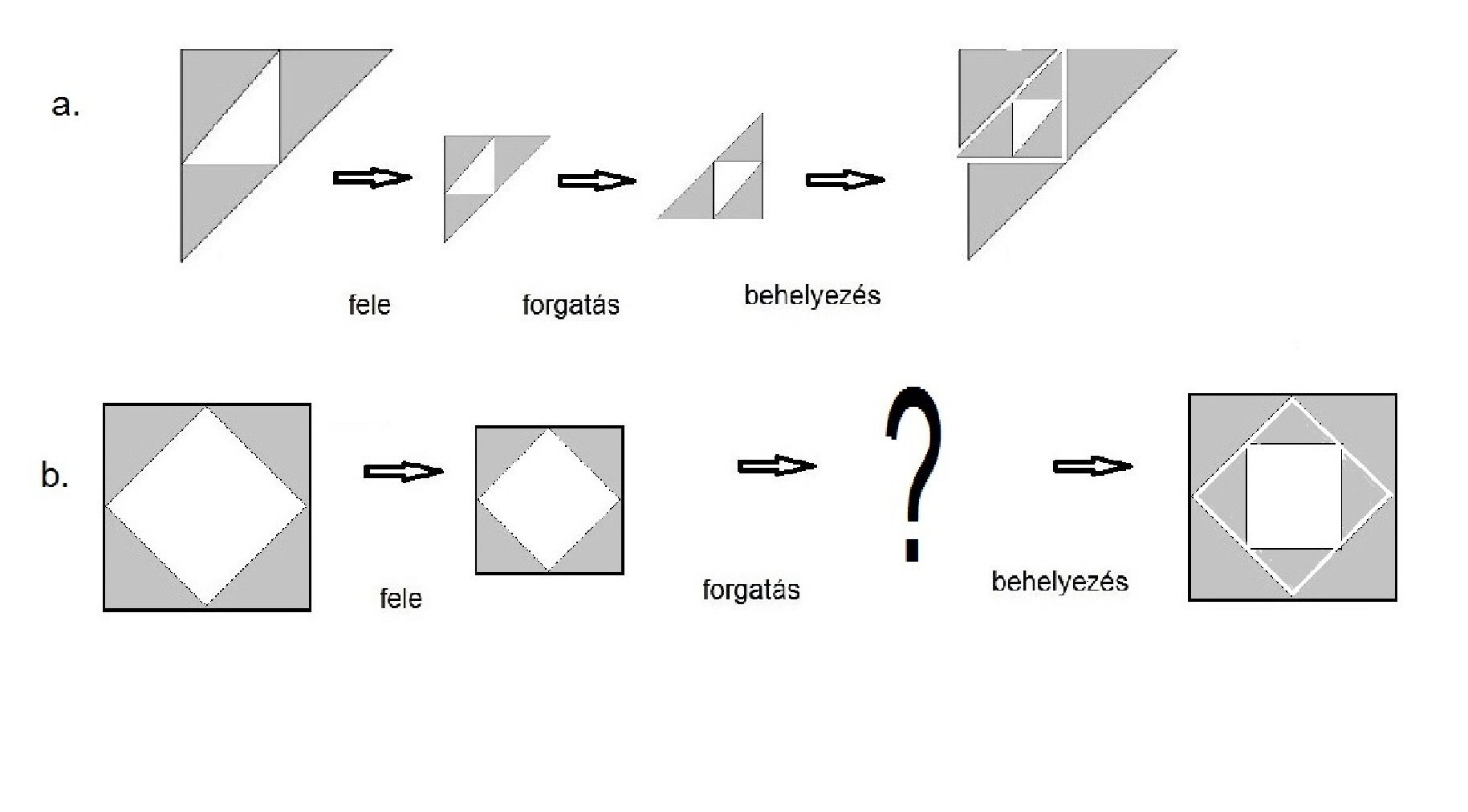
A háromszög egyre nagyobb részét befedő szürke részek területei egy olyan geometriai sorozat részletösszegei, amelynek első eleme ![]() és hányadosa
és hányadosa ![]() . Az ábrán azt mutatjuk, hogy hogyan szerkesszük a sorozat második elemét, majd az első két elem összegét. Ezután a szerkesztés ismétlésével (iterációjával) kapjuk a további részletösszegeket. Az ábrából úgy tűnik, hogy ekkor a végtelen geometriai sorozat összege a háromszög
. Az ábrán azt mutatjuk, hogy hogyan szerkesszük a sorozat második elemét, majd az első két elem összegét. Ezután a szerkesztés ismétlésével (iterációjával) kapjuk a további részletösszegeket. Az ábrából úgy tűnik, hogy ekkor a végtelen geometriai sorozat összege a háromszög ![]() területe. Ugyanis a fehéren maradó háromszög negyed akkora lesz a szerkesztés ismétlésével, a rekurzív szerkesztés minden lépése után. Formulával, a matematika nyelvén ezt kifejezve: az
területe. Ugyanis a fehéren maradó háromszög negyed akkora lesz a szerkesztés ismétlésével, a rekurzív szerkesztés minden lépése után. Formulával, a matematika nyelvén ezt kifejezve: az ![]() -edik lépes után a szürke rész területe
-edik lépes után a szürke rész területe ![]()
A mondottak alapján nem nehéz belátni, hogy a b) négyzetből indítva, az előző a) ábrához hasonló rekurzív szerkesztéssel is megkapjuk a ![]() hányadosú geometriai sorozat részletösszegét mint a szürke poligon területét.
hányadosú geometriai sorozat részletösszegét mint a szürke poligon területét.
Figyeljük meg, hogy az előző ábrák a véges, ![]() -tagú összeget is szemléltetik. Számunkra viszont (2) szemléltetése az érdekes, mivel írásunkban a határérték érzékeltetése és definıciója a cél.
-tagú összeget is szemléltetik. Számunkra viszont (2) szemléltetése az érdekes, mivel írásunkban a határérték érzékeltetése és definıciója a cél.
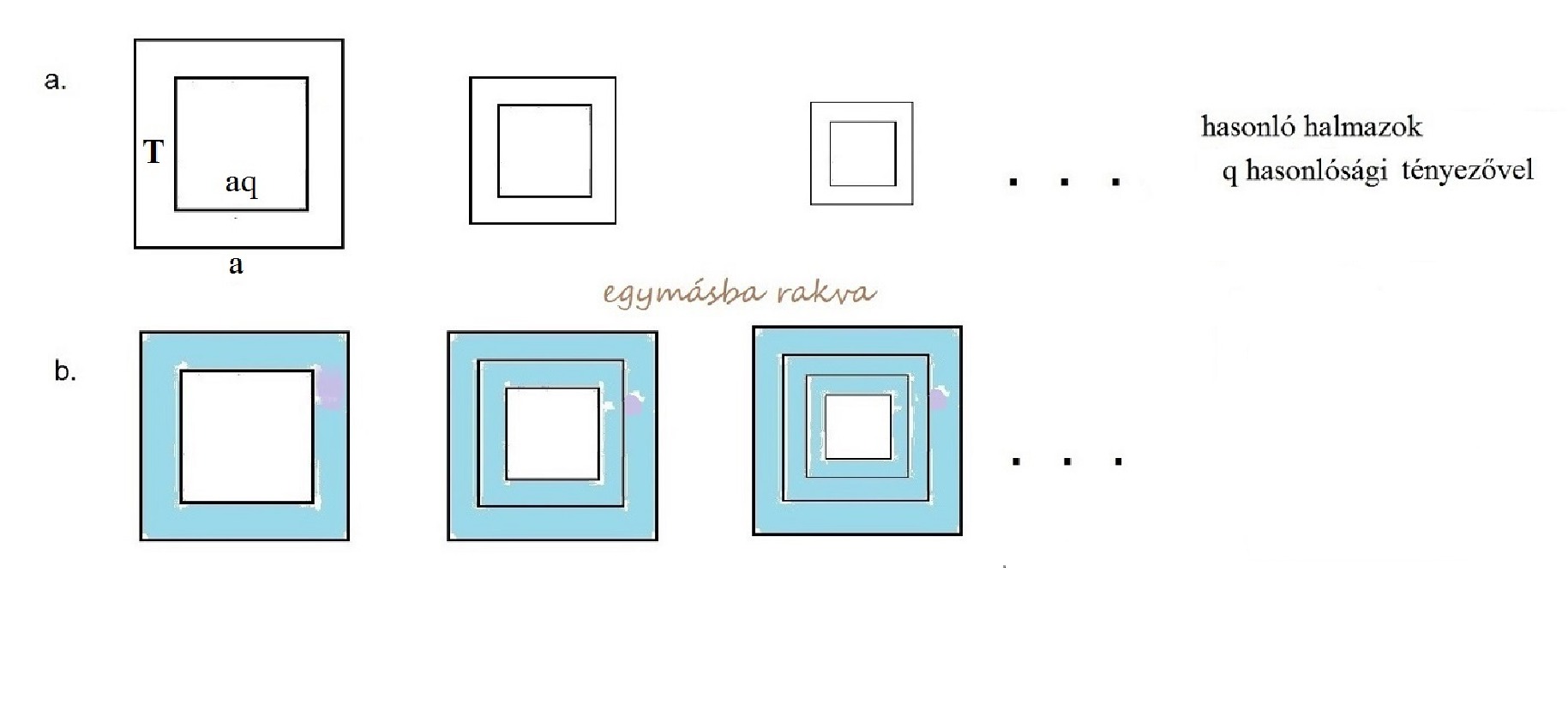
A 3. ábrán egy ![]() hányadosú geometriai sorozatot illusztrálunk képkeretszerű halmazokkal. A 3.a. ábrán, az egyre kisebb képkeretek területei egy
hányadosú geometriai sorozatot illusztrálunk képkeretszerű halmazokkal. A 3.a. ábrán, az egyre kisebb képkeretek területei egy ![]() hányadosú geometriai sorozatot alkotnak, amelynek első tagja a legnagyobb képkeret
hányadosú geometriai sorozatot alkotnak, amelynek első tagja a legnagyobb képkeret ![]() területe. Az egymással hasonló halmazokat a 3.b. ábrán látható módon egymásba skatulyázva, az egyre vastagodó kék szınű „képkeretek" területei
területe. Az egymással hasonló halmazokat a 3.b. ábrán látható módon egymásba skatulyázva, az egyre vastagodó kék szınű „képkeretek" területei
és a 3.b. ábrából leolvasható
| (3) |
mivel az ![]() -edik keret beillesztése után a fehéren maradó terület
-edik keret beillesztése után a fehéren maradó terület ![]() .
.
A 3.b. ábrán azt is láthatjuk, hogy a fehéren maradó rész egyre kisebb lesz, területe egyre közeledik a nullához. Úgy gondoljuk, hogy a fehér négyzet végül eltűnik. Ezzel egyszerű formulát kaptunk a geometriai sorozat összegére ![]() hányados esetén.
hányados esetén.
Használhatóbb képletet kapunk, ha csupán a ![]() változókkal írjuk fel a (3) formulát. A 3.a. ábrából
változókkal írjuk fel a (3) formulát. A 3.a. ábrából
hiszen ![]() annak a képkeretnek a területe, amelyet úgy kapunk, hogy az
annak a képkeretnek a területe, amelyet úgy kapunk, hogy az ![]() oldalú négyzetből kivágjuk a
oldalú négyzetből kivágjuk a ![]() oldalú négyzetet. Ebből
oldalú négyzetet. Ebből
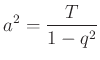
amit a (3) formulába helyettesıtve, megkapjuk az ismert, használhatóbb képletet.
Figyeljük meg, hogy körgyűrükkel, vagy háromszögekből indıtva, hasonlóan modellezhető egy geometriai sorozat összege.
Hátra van a geometriai sorozat összegének vizuális tárgyalása a ![]() esetén. Ekkor a kék szınű képkereteket belülről kifelé rakjuk össze. (Ezt nem is lehet másként, hiszen ekkor a keretek
esetén. Ekkor a kék szınű képkereteket belülről kifelé rakjuk össze. (Ezt nem is lehet másként, hiszen ekkor a keretek ![]() növekedésével egyre nagyobbak lesznek.)
növekedésével egyre nagyobbak lesznek.)
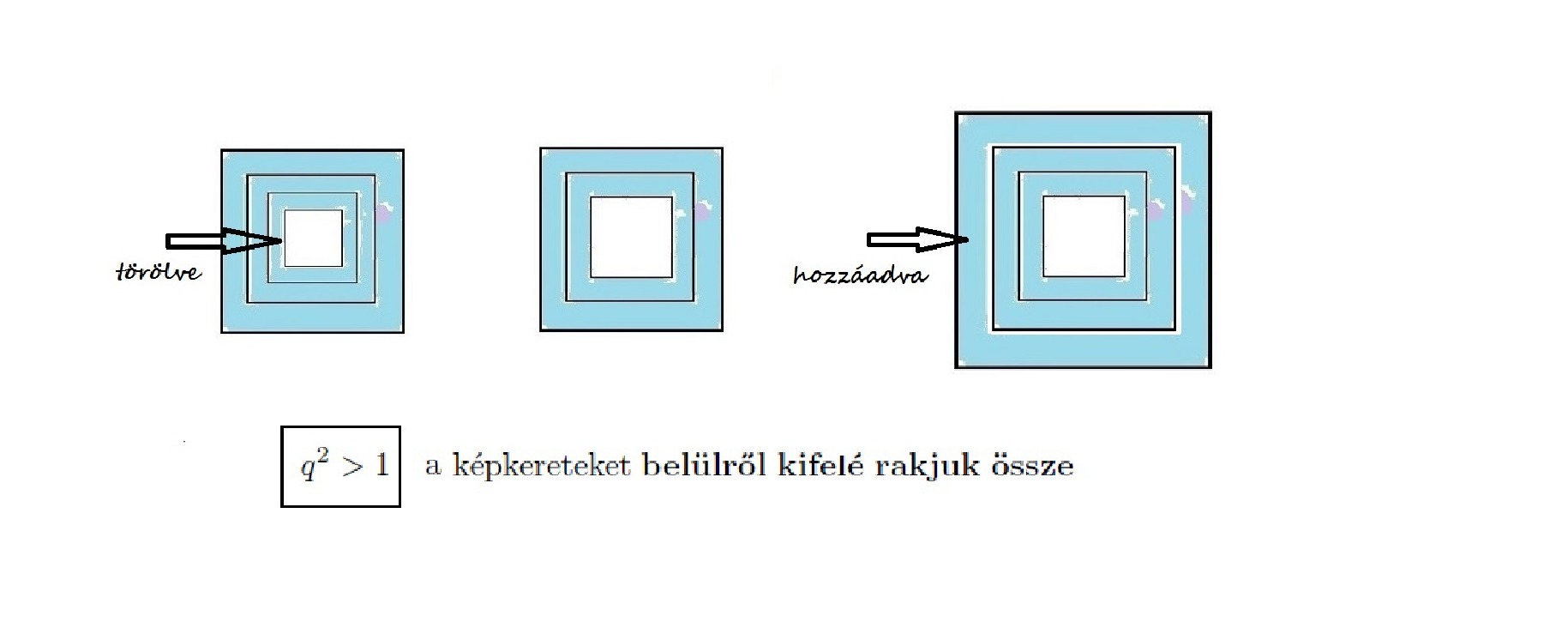
Legyen az összerakott keret területe, vagyis a (3) baloldalán álló összeg, ![]() . Töröljük az első keretet és adjuk hozzá a következő,
. Töröljük az első keretet és adjuk hozzá a következő, ![]() -edik keretet (4. ábra). Az így kapott halmaz területe
-edik keretet (4. ábra). Az így kapott halmaz területe ![]() . A matematika nyelvén ezt leírva
. A matematika nyelvén ezt leírva
| (4) |
A (4) formulából, az ![]() területet kifejezve, megkapjuk a geometriai sorozat (1) összegképletét.
területet kifejezve, megkapjuk a geometriai sorozat (1) összegképletét.
A 4. ábrán illusztrált modell egy univerzális modell, mivel ![]() alkalmas megválasztásával, minden pozitıv hányadosú geometriai sorozat összege illusztrálható az ábrával. Hasonlóan szerkeszthető univerzális modell körből, háromszögből és különböző sokszögekből.
alkalmas megválasztásával, minden pozitıv hányadosú geometriai sorozat összege illusztrálható az ábrával. Hasonlóan szerkeszthető univerzális modell körből, háromszögből és különböző sokszögekből.
Figyeljük meg, hogy ![]() esetén a szürke színű képkeretek területe bármely számnál nagyobb lesz, ha elég messze megyünk a képkeretek sorozatában.
esetén a szürke színű képkeretek területe bármely számnál nagyobb lesz, ha elég messze megyünk a képkeretek sorozatában.
Hasonlítsuk össze a mondottakat a geometriai sorozat (1) összegképletének hagyományos bizonyításával. Ha
akkor
Kivonva egymásból a két egyenlőséget
amelyet ![]() -re rendezve adódik (1). Vegyük észre, hogy a (4) formulára vezető szerkesztés a hagyományos bizonyításnak egy vizuális megjelenıtése, a hagyományos bizonyítás szemléltetése.
-re rendezve adódik (1). Vegyük észre, hogy a (4) formulára vezető szerkesztés a hagyományos bizonyításnak egy vizuális megjelenıtése, a hagyományos bizonyítás szemléltetése.
A végtelen geometriai sorozatotot illusztráló geometriai modell tárgyalásában fontos szerepe van a következő megállapıtásnak: „Úgy gondoljuk, hogy a fehér négyzet végül eltűnik.''. Pontosítsuk ezt az intuitív megállapítást és írjuk le a matematika nyelvén. Könnyen belátható, hogy a következő megállapítás kifejezi ezt az intuitív szemléletet: a fehéren maradó négyzet átmérője tetszőlegesen kicsi lesz, ha elég messze megyünk a képkeretek sorozatában. A matematika nyelvén:
Minden ![]() számhoz van
számhoz van ![]() , hogy ha
, hogy ha ![]() akkor
akkor
![]()
ahol ![]() , mint eddig, az
, mint eddig, az ![]() tagú részletösszeg.
tagú részletösszeg.
A következő példával illusztráljuk, hogy a szöveg és a matematikai formulák ugyanazt mondják. Legyen ![]() , vagyis azt kérdezzük, hogy milyen messze menjünk a sorozatban, hogy a képkeretek területe legfeljebb egyszázaddal térjen el a négyzet területétől. Erre a kérdésre az
, vagyis azt kérdezzük, hogy milyen messze menjünk a sorozatban, hogy a képkeretek területe legfeljebb egyszázaddal térjen el a négyzet területétől. Erre a kérdésre az
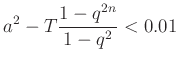
egyenlőtlenség megoldása adja a választ. Ha ![]() ,
, ![]() akkor
akkor ![]() és így a választ az
és így a választ az
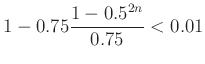
megoldása adja. A negyedik tagon túl a képkeretek területe legfeljebb egyszázaddal tér el egytől, a négyzet területétől.
Végtelen geometriai sorozat egy tábla szelvényes csokoládéban
Egy csokoládét úgy reklámoz a gyártója, hogy minden tábla csokoládéhoz mellékel egy szelvényt, amelyből bizonyos mennyiséget összegyüjtve, az összegyüjtött szelvényekért egy újabb tábla csokoládét kap a vásárló. Egy tábla csokoládé ára 175 Ft, és öt szelvényért kapunk még egy tábla csokoládét.
Mennyibe kerül valójában egy tábla csokoládé?
Egy tábla csokoládé áráért, 175 forintért, a tábla csokoládé mellé még egy szelvényt is kapunk. Ezért ha a csokoládé ![]() forintot és egy szelvény
forintot és egy szelvény ![]() forintot ér, akkor nyilván
forintot ér, akkor nyilván
| (5) |
és mivel öt szelvényért kapunk egy tábla csokoládét, amelyhez egy újabb szelvény tartozik, ezért
| (6) |
Az (5), (6) egyenletrendszerből ![]() .
.
Mi köze van ennek az egyszerű csokoládépéldának egy geometriai sorozat összegéhez?
A szelvény ![]() értéke egy geometriai sorozat összegeként is előáll a következőképpen. A (6) összefüggés szerint, egy szelvény
értéke egy geometriai sorozat összegeként is előáll a következőképpen. A (6) összefüggés szerint, egy szelvény ![]() csokoládét meg
csokoládét meg ![]() szelvényt ér (5. ábra). Így a
szelvényt ér (5. ábra). Így a ![]() szelvény
szelvény ![]() csokoládét meg
csokoládét meg ![]() szelvényt ér. Tovább folytatva ezzel a gondolatmenettel:
szelvényt ér. Tovább folytatva ezzel a gondolatmenettel: ![]() szelvény értéke
szelvény értéke ![]() csokoládé meg
csokoládé meg ![]() szelvény és így tovább a végtelenségig.
szelvény és így tovább a végtelenségig.

A matematika nyelvén a fenti rekurzív gondolatmenet így írható
| (7) |
azaz
és teljes indukcióval
Így a szelvény ![]() értéke a
értéke a ![]() -ből induló,
-ből induló, ![]() hányadosú (végtelen) geometriai sorozat összege.
hányadosú (végtelen) geometriai sorozat összege.
Mi történt eddig?
Különböző nézőpontból és különböző készségekre épıtve tárgyaltuk a geometriai sorozat összegezését.
Geometriai modellekkel kezdtünk, amelyben a geometriai sorozat elemei olyan egymással hasonló körök, sokszögek, amelyek egymásba skatulyázhatók, és ismert területű halmazt töltenek ki. Ezzel nemcsak a részletösszegek alakulását szemléltetjük, hanem felvillantjuk a hasonlóság és a geometriai sorozat kapcsolatát is. Ez a szemléltetés szoros kapcsolatban van az ókori görög matematikából származó kimerítés módszerével.
Összehasonlítottuk az univerzális matematikai modellt az (1) összegképlet szokásos bizonyításával, amely arra a megfigyelésre épít, hogy a ![]() hányadossal szorozva, a geometriai sorozat elemeit egy lépéssel előre toljuk. Ezzel egy szemléletes, geometriai megfogalmazását adtuk az (1) összegképlet szokásos bizonyıtásának.
hányadossal szorozva, a geometriai sorozat elemeit egy lépéssel előre toljuk. Ezzel egy szemléletes, geometriai megfogalmazását adtuk az (1) összegképlet szokásos bizonyıtásának.
A csokoládépélda egy manipulatív modell, amely valamilyen történéshez köti a problémát. A csokoládépéldát, némi változtatással, Péter Rózsa [4] könyvéből vettem. Figyeljük meg a geometriai modell és a csokoládépélda kapcsolatát.
Az elmondottakban végigvonul az intuitív szemlélet és a matematikai formulák kapcsolata. Figyeljük meg, hogyan fejeztünk ki egy tapasztalt összefüggést a matematika nyelvén és fordítva, matematikai formulákkal leírt összefüggésekhez hogyan gyártottunk kézzelfogható modelleket.
Furcsaságok a végtelenben
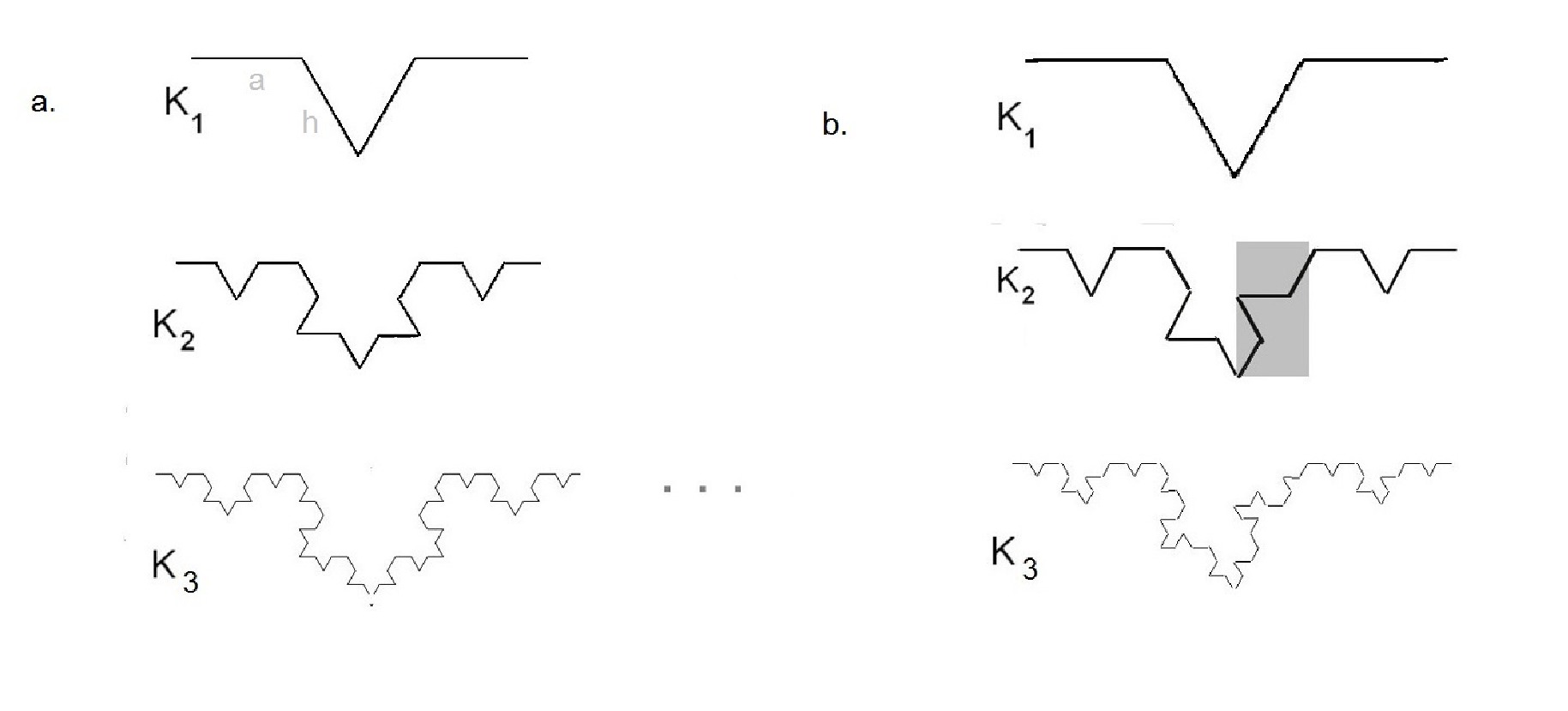
A 6.a. ábrán látható egyszerű ![]() töröttvonalból indıtunk. A töröttvonal négy egyenesszakasz egyesıtése (uniója), amelyek mindegyike a
töröttvonalból indıtunk. A töröttvonal négy egyenesszakasz egyesıtése (uniója), amelyek mindegyike a ![]() átmérőjének a harmada. Most cseréljünk le minden egyenesszakaszt a
átmérőjének a harmada. Most cseréljünk le minden egyenesszakaszt a ![]() töröttvonal harmadára kicsinyıtett másával. Ekkor kapjuk a
töröttvonal harmadára kicsinyıtett másával. Ekkor kapjuk a ![]() töröttvonalat. A
töröttvonalat. A ![]() a
a ![]() -gyel hasonló négy töröttvonal uniója, amelyeknek a hasonlósági tényezője egyharmad. A
-gyel hasonló négy töröttvonal uniója, amelyeknek a hasonlósági tényezője egyharmad. A ![]() töröttvonalat ugyanígy kapjuk
töröttvonalat ugyanígy kapjuk ![]() -ből. A
-ből. A ![]() -ben minden egyenesszakaszt lecserélünk a
-ben minden egyenesszakaszt lecserélünk a ![]() megfelelően kicsinyített másával, vagyis egy
megfelelően kicsinyített másával, vagyis egy ![]() -el hasonló töröttvonallal, amelynek hasonlósági tényezője
-el hasonló töröttvonallal, amelynek hasonlósági tényezője ![]() . És ezt folytatjuk a végtelenségig.
. És ezt folytatjuk a végtelenségig.
Hogyan alakul a töröttvonalak hossza a kapott sorozatban?
A szerkesztésből következik, hogy mindegyik töröttvonal hossza az előző hosszának négyharmada. Így, a ![]() átmérőjével mérve
átmérőjével mérve
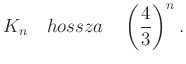
A ![]() hossza bármely értéknél is nagyobb lehet, ha a szerkesztést elég hosszan folytatjuk, ha elég messze megyünk a
hossza bármely értéknél is nagyobb lehet, ha a szerkesztést elég hosszan folytatjuk, ha elég messze megyünk a ![]() sorozatban. Mégis, a
sorozatban. Mégis, a ![]() sorozat minden eleme elfér egy olyan körben, amelynek átmérője megegyezik a
sorozat minden eleme elfér egy olyan körben, amelynek átmérője megegyezik a ![]() átmérőjével.
átmérőjével.
Az 6.b. ábrán a szerkesztést kissé megváltoztattuk. A ![]() -ben az egyik egyenesszakaszt a
-ben az egyik egyenesszakaszt a ![]() tükörképével cseréltük le ( szürkével fedett rész). A töröttvonal hossza változatlan maradt, de a kapott sorozat képe drasztikusan megváltozott. Ily módon szimulálni tudunk különböző zeg-zugos partvonalat.
tükörképével cseréltük le ( szürkével fedett rész). A töröttvonal hossza változatlan maradt, de a kapott sorozat képe drasztikusan megváltozott. Ily módon szimulálni tudunk különböző zeg-zugos partvonalat.
Ha ![]() átmérőjét az egyszázadára csökentjük és ezzel a töröttvonallal végezzük a szerkesztést, akkor is tetszőlegesen nagy lesz a töröttvonal hossza, csupán ekkor tovább kell folytatnunk a szerkesztést, messzebb kell elmenni a
átmérőjét az egyszázadára csökentjük és ezzel a töröttvonallal végezzük a szerkesztést, akkor is tetszőlegesen nagy lesz a töröttvonal hossza, csupán ekkor tovább kell folytatnunk a szerkesztést, messzebb kell elmenni a ![]() sorozatban, hogy a
sorozatban, hogy a ![]() hossza az adott értéknél nagyobb legyen. Ily módon bármilyen kis átmérőjű körbe berajzolhatunk tetszőlegesen hosszú töröttvonalat. Ennek a szerkesztésnek a végeredményét Koch-görbének nevezik.
hossza az adott értéknél nagyobb legyen. Ily módon bármilyen kis átmérőjű körbe berajzolhatunk tetszőlegesen hosszú töröttvonalat. Ennek a szerkesztésnek a végeredményét Koch-görbének nevezik.

A 7. ábrán, ugyanezzel a szerkesztéssel, egy háromszögből indıtunk. A kapott ![]() sorozat ekkor egy a Koch-szigetre vezet. Azt is mondhatjuk, hogy a Koch-sziget egy háromszög oldalaira illesztett három Koch-görbe uniója (egyesıtése). A Koch-sziget területe véges és legfeljebb a
sorozat ekkor egy a Koch-szigetre vezet. Azt is mondhatjuk, hogy a Koch-sziget egy háromszög oldalaira illesztett három Koch-görbe uniója (egyesıtése). A Koch-sziget területe véges és legfeljebb a ![]() Dávid csillag területének duplája.
Dávid csillag területének duplája.
Érdemes elgondolkodni azon, hogy ha a ![]() töröttvonalban, az egyenlőoldalú háromszög szárait egy tetszőleges
töröttvonalban, az egyenlőoldalú háromszög szárait egy tetszőleges ![]() magasságú egyenlőszárú háromszög száraira cseréljük, akkor milyen változás történik a szerkesztett töröttvonalak hosszában és alakjában.
magasságú egyenlőszárú háromszög száraira cseréljük, akkor milyen változás történik a szerkesztett töröttvonalak hosszában és alakjában.
Geometriai sorozatot alkotó lépcsők. A pókhálódiagram
A geometriai sorozat természetes felírása a
| (8) |
rekurzív formula, hiszen (8) pontosan azt fejezi ki, hogy az egymás után következő számok hányadosa ![]() . A (8) rekurzív formula inspirálja a 8. ábra rekurzív szerkesztését, amit web vagy hálódiagramnak is neveznek.
. A (8) rekurzív formula inspirálja a 8. ábra rekurzív szerkesztését, amit web vagy hálódiagramnak is neveznek.
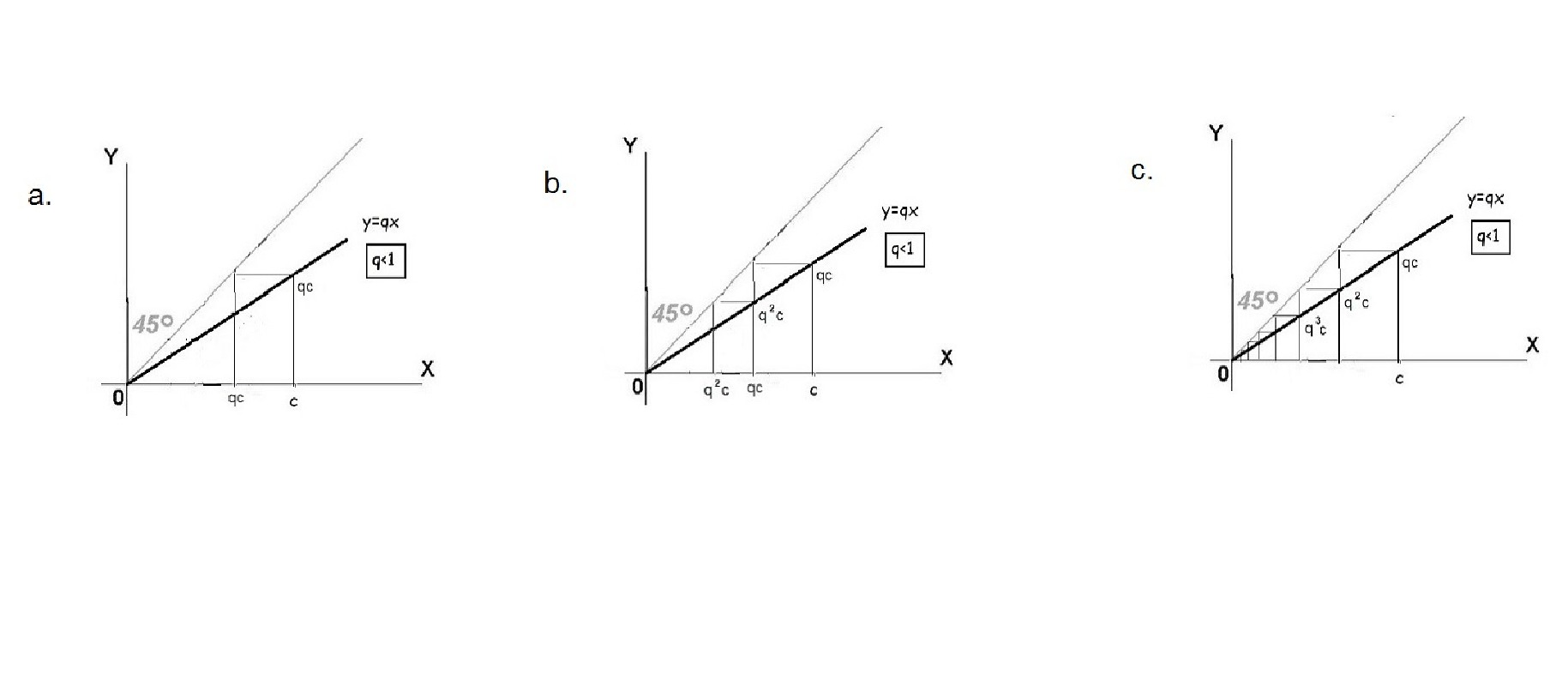
Az a) ábra mutatja az első lépést, majd a b) ábrán látható ennek rekurzív folytatása. A c) ábra a teljes szerkesztést jelzi ![]() esetén. A szerkesztéssel kapott lépcsők befutnak az origóba, ami intuitíve jelzi, hogy a (8) sorozat nullához tart. Ez azt jelenti, hogy ha elég messze megyünk a sorozatban, akkor tetszőlegesen közel kerülhetünk a nullához (a
esetén. A szerkesztéssel kapott lépcsők befutnak az origóba, ami intuitíve jelzi, hogy a (8) sorozat nullához tart. Ez azt jelenti, hogy ha elég messze megyünk a sorozatban, akkor tetszőlegesen közel kerülhetünk a nullához (a ![]() origóhoz).
origóhoz).
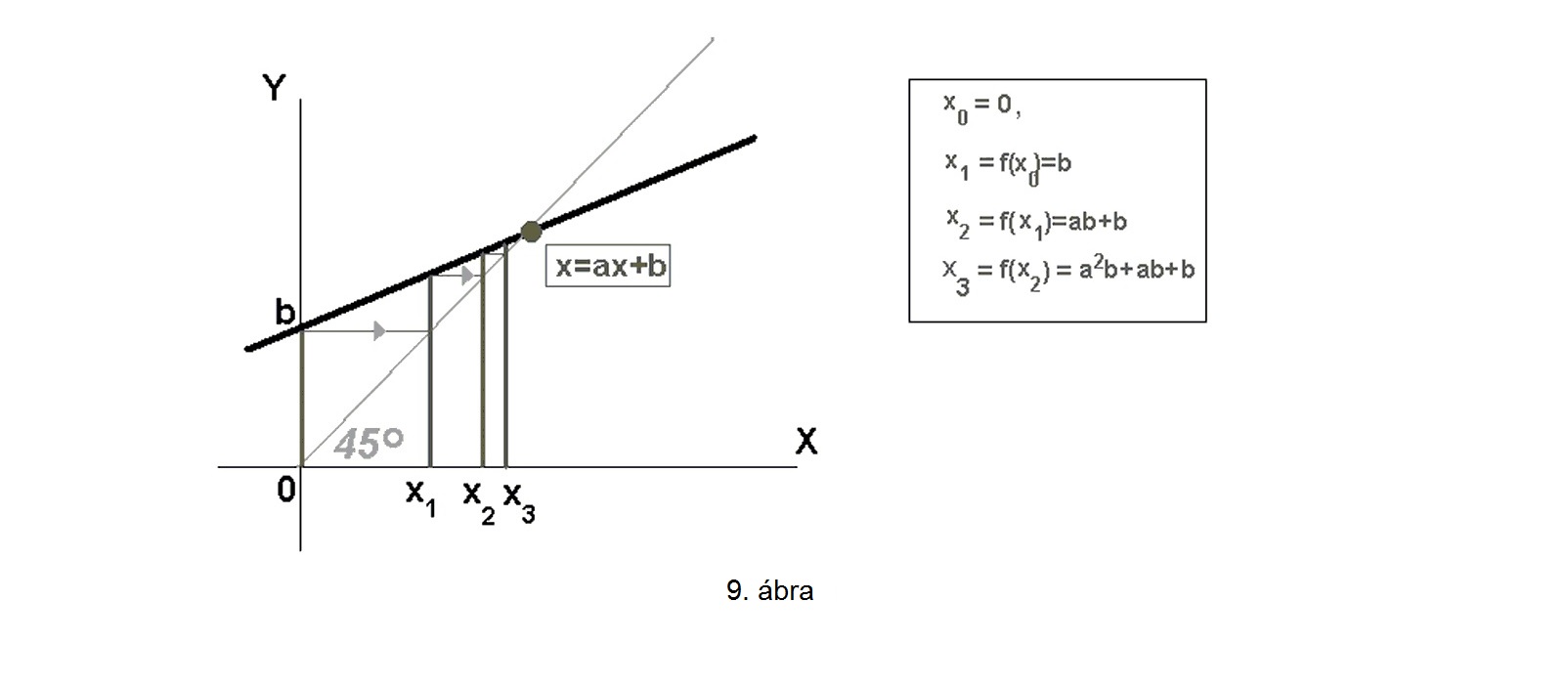
Érdemes megvizsgálni, hogy ha ![]() helyett egy tetszőleges
helyett egy tetszőleges ![]() egyenessel végezzük ezt a szerkesztést, akkor milyen sorozatot kapunk? Mi a szerepe ekkor az egyenes és a
egyenessel végezzük ezt a szerkesztést, akkor milyen sorozatot kapunk? Mi a szerepe ekkor az egyenes és a ![]() -os egyenes metszéspontjának?
-os egyenes metszéspontjának?
- Irodalomjegyzék
- 1
- Barnsley, Michael F.: Fractals Everywhere, Academic Press, Orlando, FL, 2012 (3. kiadás).
- 2
- Dehaene, Stanislas: The number sense: How the mind creates mathematics, OUP USA, 2011 (3. angol kiadás 2011). (Magyarul: A számérzék: Hogyan alkotja meg az elme a matematikát?, Osiris, Budapest, 2003.)
- 3
- Németh József: Előadások a végtelen sorokról, POLYGON, Szeged, 2002
- 4
- Péter Rózsa: Játék a végtelennel, TYPOTEX, Budapest, 2010 (9. kiadás).
Máté LászlóBME Analízis Tanszék