0. Bevezető
Ez a rövid cikk alapvetően didaktikai szándékú és fő célja, hogy megmutassa a XX. század egyik legkiemelkedőbb magyar matematikusának, Neumann Jánosnak egy igazán világraszóló eredményét, pontosabban az ahhoz vezető fő gondolatokat, amit ma „Minimax-tételnek” vagy a játékelmélet alaptételének is neveznek. A leírtak alapján akár egy középiskolai kísérleti kipróbálást is meg lehet szervezni, amit a szerző meg is tett évekkel ezelőtt több vidéki és fővárosi iskolában.
Két, nem csak a matematikus világban világhírűvé vált János született majdnem pontosan 100 év különbséggel a XIX. és a XX. században. Mindketten a világon valaha élt legjelentősebb matematikusok közé tartoznak. Ezért is fontos lenne az iskolában mindkettőjükről beszélni, hiszen magyar tanuló számára a matematika szó elhangzásakor legalább ezek a nevek be kellene, hogy ugorjanak. Egyikük Bolyai János (1802-1860), akinek a nem-euklideszi geometriát köszönhetjük, s amelynek iskolai bemutatása először Lénárt István[1] gömbjeivel vált lehetővé. Bolyai elismerése tragikus élete során nem, csak halála után kezdődött, igaz azóta is töretlen.
Eredménye a modern matematika egyik előfutárává tette, aki évtizedekkel megelőzte korát. Ennek az úttörő szerepnek a bemutatására egy tudományelméleti megközelítést választó beszélgetésre utalnék, amely Staar Gyula könyvében [1] olvasható a Tóth Imrével folytatott dialógusban. Munkásságának igazi jelentősége remekül kiviláglik Tóth matematika filozófiai fejtegetéséből. Az olvasónak ajánljuk a beszélgetés megismerését.


Két játékos játszik úgy, hogy mindkettőnek két lehetősége van, vagy tesz egy pénzérmét a kezébe vagy nem. Majd mindketten előrenyújtják az összezárt kezüket és egyszerre kinyitják. Az első, nevezzük őt A játékosnak, nyer, ha a két kéz szimmetrikus, azaz mindkettő üres vagy mindkettőben van egy-egy érem. A másik, B nyer, ha aszimmetrikus, azaz ha az egyikben van pénzérme, míg a másikban nincs. Abban is hasonlít a játék a snóblira, hogy a nyeremény a kezekben levő pénzérmék összege. De mivel, ha senki nem tett, akkor 0 lenne a nyeremény, ezért a pénzérmékhez a vesztes még egyet hozzátesz. Így az alábbi, ún. kifizetési mátrixszal írhatjuk le a játékot:
| ↓ A játékos; B játékos téte → | 0 | 1 |
| 0 | 1 | -2 |
| 1 | -2 | 3 |
A kérdések a következők:
- ) Milyen stratégiát kövessenek a játékosok?
- ) Igazságos-e a játék vagy valakinek kedvez?
A kérdések megválaszolását megelőzheti a játék kipróbálása, amelynek tapasztalatait a következőkben összegezzük.
2. A játék elemzése stratégiai szempontból
Mindkét játékos számára fontos, hogy kiismerhetetlen legyen a játéka, mivel ellenkező esetben veszteni fog, bármelyik szerepben is van. Pl. ha A tudja mit fog lépni B, akkor ugyanazt teszi ő is, hiszen szimmetrikus esetben ő nyer. Ugyanez igaz B-re is, csak ő ekkor éppen ellenkezőképpen fog cselekedni, s nyer. Azaz mindkettőjük számára fontos a kiismerhetetlenség. De hogyan is lehet a viselkedésem kiismerhetetlen? Ha véletlenszerű, hiszen ekkor nem tudja a másik, mi fog történni. Bármilyen rafinált determinisztikus stratégiával is játszom, egy idő múlva felismeri a másik, s meg tudja jósolni a következő lépésemet. A nem tét és a tét egy 0, 1 sorozattal írható le. Ha akár A, akár B felismer valami szabályszerűséget partnere 0, 1 sorozatában, akkor onnantól kezdve nyerni fog. Ezzel azonban még csak az első lépést tettük meg Neumann János gondolatmenetében. Itt jegyezzük meg azt, hogy a véletlennek egy lehetséges meghatározása éppen a bonyolultság segítségével lehetséges. Ha egy 0, 1 sorozatot nem lehet lényegesen rövidebb hosszúságú programmal leírni, mint a sorozat elemeinek száma, akkor mondjuk véletlennek sorozatnak. Ezzel ma egy új matematikai elmélet a bonyolultságelmélet foglalkozik, melyet nem meglepően éppen az a matematikus kezdeményezett Chatain amerikai kollégájával, aki a valószínűségszámítás matematikai megalapozását is elvégezte, azaz A. N. Kolmorogov[3]. Egy Lovásztól származó egyetemi jegyzet 6. fejezetében olvashatunk erről bővebben, lásd [4] 109. oldaltól.
A következő kérdés persze az, hogy milyen véletlen generátorral játsszak. Más szavakkal, mi legyen a „teszek a kezembe pénzt” vagy a „nem teszek” valószínűsége? Vajon léteznek-e olyan valószínűségértékek, amelyek „optimálisak” abban az értelemben, hogy a tőlük való eltérés hátrányos a játékos(ok)nak. Elemezzük a helyzetet. Ha a két játékos egymástól függetlenül p és q valószínűséggel tesz pénzérmét a kezébe, akkor az A játékos nyereményének várható értéke a két egyelőre ismeretlen valószínűséggel a következőképpen írható fel:
(1)
Két dolgot használtunk fel, a várható (nyeremény)érték fogalmát, valamint az események függetlensége esetén fennálló szorzási szabályt. Tehát, hogy például A tesz és B nem tesz, annak esélye éppen . Vizsgáljuk most meg ezt a kifejezést.
Egyúttal vegyük észre, hogy B várható nyereménye éppen , azaz amikor B nyereménye maximális, akkor A nyereménye minimális és fordítva, mivel pénzt csak egymástól nyernek el. Ha nincs se külső pénzforrás, se pénznyelő, akkor az ilyen játékokat szokás zérusösszegű játéknak nevezni, mivel a játékosok „nyereményeinek” összege mindig 0. Mielőtt tovább vizsgálnánk a helyzetet, alakítsuk át (1)-et, a beszorzások elvégzésével és az egynemű tagok összevonásával adódik
(2) .
Iskolás feladat, hogy egy kifejezést alakítsunk szorzattá, lehetőleg úgy, hogy az egyik tényezőben csak a p, a másikban csak a q szerepeljen. Így kapjuk
(3)
Most kezdhetjük bemutatni Neumann János gondolatát, amelyben feltételezi, hogy mindkét játékos intelligens, s a számára legjobb megoldást képes választani. A feltételezi, hogy B nagyon okos, tehát olyan q értéket választ, ami mellett nyeresége maximális, azaz A nyereménye minimális. Ezután jön a saját „okossága”, ami olyan p választást jelent, hogy a nyereménye maximális legyen. Ezt úgy fejezhetjük ki, hogy keressük a következő kettős szélsőértéket: . Ugyanez B szemszögéből
. Akkor van optimális megoldás mindkét játékosnak, ha a két szélsőértékhely egybeesik. Neumann éppen azt bizonyította, hogy két játékos zérusösszegű játéka esetén mindig vannak olyan valószínűségek a döntési lehetőségeik halmazán, amely mindkettőjüknek a lehető legjobb. Ha ilyenkor a nyeremény várható értéke 0, akkor igazságosnak mondjuk a játékot. Az optimumot az egységnégyzeten ábrázolt felületet szemlélve, amit az
függvény grafikonja rajzol ki, érthető, miért hívjuk nyeregpontnak.

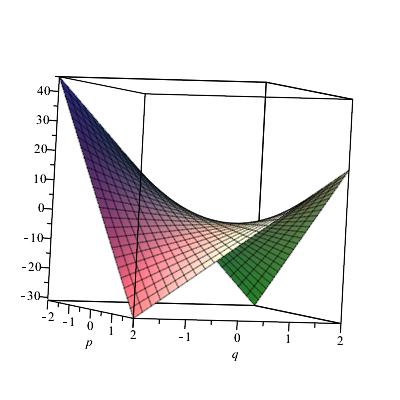 Lásd a mellékelt két ábrát illusztrációként.
Lásd a mellékelt két ábrát illusztrációként.
Neumann számára az ötletet, amelyből kiindulhatott, a Young-tétel adhatta, mely szerint a kétváltozós függvény változók szerinti parciális deriváltjainak esetében a deriválás sorrendje felcserélhető, formálisan: . Egyébként ezt a (2)-beli kifejezésünkön elvégezve is láthatjuk. Ha először p szerint deriválunk, a másik változót paraméternek véve, akkor kapjuk:
. Ezt tovább deriválva, most q szerint, adódik 8. Ha fordított sorrendben végezzük el a parciális deriválást, akkor első lépésben
adódik, s ezt most p szerint deriválva, szintén 8 lesz az eredmény. A tételnek természetesen feltételei vannak, amelyek esetünkben teljesülnek. Ennek általában egy n változós analógiája szükséges, lásd a 3. paragrafusát ennek a cikknek. Ezen túl azt is igazolni kell, hogy a szélsőérték az egységnégyzet (egység-hiperkockába) belsejébe vagy legfeljebb a határára esik, mivel itt valószínűségek szerepelnek, melyek 0 és 1 közé kell, hogy essenek. Erre még visszatérünk.
Először vizsgáljuk meg a (3) kifejezést. Itt világos, hogy mivel a két paraméter különböző tényezőkben szerepel, látszik, hogy a másik játékától egy módon függetleníthetem magam, ha a saját tényezőmet 0-vá teszem, mert akkor a szorzat a másiktól függetlenül 0 lesz. Azaz mindkettőnek ez célszerű választás (esetünkben p = 3/8 és q = 3/8), hiszen ilyenkor nem is kell a másikat figyelni. Azonban az is látható, hogy bármelyiküknek veszteséges lehet az ettől való eltérés, ha a másik elég intelligens. Akár A, akár B szempontjából elvégezhetjük az eltérést a fentebb meghatározott p és q értéktől akár felfelé, akár lefelé. Egy esetet bemutatunk, a másik hármat az olvasó is elvégezheti. Tehát pl. A játékos felfelé eltér a p = 3/8 értéktől. Ezt, ha sokszor játszanak a megfelelő relatív gyakoriságból észreveszi B. Mivel neki a függvény minél kisebb értéke a célja (ha A nyeresége minimális, akkor az övé maximális) ezért ő lefelé fog eltérni a q = 3/8 értéktől. Ekkor mivel a szorzat negatív lesz (ezért tér el éppen ellentétes irányban, mint A) több, mint 1/8 lesz a nyeresége átlagosan partinként. Tehát ha A intelligens, akkor jobb, ha nem tér el felfelé a 3/8-tól. ugyanez igaz a lefelé eltérésre is. Ezért nevezzük ezt optimális értéknek számára. Hasonló érveléssel mondható el ez B-ről is. Azaz mindenféle mélyebb analízis ismeret nélkül, pusztán elemi algebrai okoskodással ebben az esetben megmutatható, hogy van mindkettő számára optimális valószínűség és ezzel játszva, a játék partinként átlagosan 1/8 egységet hoz B-nek. Tehát a játék nem igazságos. Ha választhatunk, akkor B szerepét kell kérnünk. Jó gyakorlás annak meggondolása, hogy a mi kifizetési mátrixunkban egyetlen szám megváltoztatásával, hogyan lehetne elérni az igazságosságot.
Megjegyeznénk azonban egy „hamis okoskodást”, amellyel amellett lehetne érvelni, hogy ez volt az igazságos. B mindenképpen 2 egységet nyer, ha nyer. A átlagosan szintén 2 egységet, mivel 1 és 3 átlaga is 2. Ezért sokan igazságosnak gondolják a játékot. A hiba ebben a gondolatban az, hogy nem a p = ½ az optimális stratégia, ezért A nem az átlagot nyeri partinként átlagosan!
3. Az egyszerű 2x2-es játék általánosítása és az alaptétel kimondása
A bemutatott és elemzett játék egyszerű általánosítása, ha nem csak két lehetőség van a játékosok számára, hanem több, pl. mindegyik tehet 1 vagy 2 vagy 3 érmét is. Ekkor mindkettőnek 4 lehetősége van. Ehhez is kell egy kifizetési mátrixot rendelni, s akkor megkérdezhető, hogy ezúttal miként játszanak. Egy példát adjunk erre a következő mátrix segítségével, folytatva a szimmetrikus A és az aszimmetrikus B játékos elvét és a pénzérmék összege plusz egy elvet a nyeremény meghatározásához. Ezt követve kaphatjuk meg a következő kifizetési mátrixot vagy inkább táblázatot:
| ↓ A játékos; B játékos téte → | 0 | 1 | 2 | 3 |
| 0 | 1 | -2 | -3 | -4 |
| 1 | -2 | 3 | -4 | -5 |
| 2 | -3 | -4 | 5 | -6 |
| 3 | -4 | -5 | -6 | 7 |
A nyeremény várható értékét kell itt is felírni, ahol az A játékos négy lehetséges választásának esélyei legyenek ,míg hasonlóan a B játékoséi:
. Ezekkel a jelölésekkel kapjuk:
(4)
továbbá .
Azonban most lesz egy nagy nehézség az eddig bemutatott módszerrel kapcsolatban, nevezetesen most már legalább három p és q érték kell, azaz 6 ismeretlenes lesz a várható nyeremény-függvény, egyet a két feltétel miatt kifejezhetünk a többivel. Ennek szemléltetésére egy hétdimenziós térre lenne szükségünk. Így a „nyeregpont” már nem látszik, ezért a szemléletes megoldás kiesik, másrészt a fentebb leírt szorzattá bontás esetleg akár több tényezővel, de úgy, hogy ezek közül egyesek csak p-ket, mások pedig csak q-kat tartalmaznak, nem vezet eredményre. Már a kisebb háromszor kettes esetben is baj van, tehát ha csak az egyiknek van 3 lehetősége. Ezekben az esetekben már komolyabb eszközökre van szükség, amelyet ma éppen pl. a számítógépek segítségével lehet elvégezni. Az alaptétel szerint ilyenkor is van optimális valószínűség-eloszlás a lehetőségeink halmazán, amelytől sem A, sem B nem tér el, ha intelligens játékosok. Neumann tétele tehát az egzisztenciáról szól, ezt sikerült belátnia még 1928-ban megjelent cikkében [5]. A tétel a következő:
Ha van egy kétszemélyes zérusösszegű játék, akkor mindig létezik mindkét játékos számára olyan optimális kevert[4] stratégia, amelytől való eltérés nem kedvező, azaz mindig létezik nyeregpontja a játéknak. Ez az ún. Minimax (Maximin)-tétel, vagy a játékelmélet alaptétele.
Az eloszlás numerikus kiszámítása azonban bonyolult feladat. Az egzisztenciát eredetileg topologikus módszerekkel sikerült Neumannnak igazolnia, mára azonban egészen más módszerek is léteznek, amelyek közül egy már a Morgensternnel írt közös könyvben [3] is megjelenik. A téma történetét elég részletesen ismerteti Kóczy Á. László cikke [6], amelyben beszámol a máig nyúló fejlődéséről is. Csupán az érdekesség kedvéért jegyezzük meg, hogy végül a téma első Nobel- díjasa az a John F. Nash[5] lett, aki a nemkooperatív játékok egyensúlyi állapotainak vizsgálata során végzett úttörő munkásságáért, főleg annak jelentős közgazdasági alkalmazásai miatt megosztva közgazdasági Nobel díjat kapott a magyar származású, Harsányi Jánossal, valamint R. Seltennel 1994-ben. Ez a terület a Neumann-féle elmélet egyik általánosítása.

Milyen meglepő, hogy Harsányi János is éppen a legendás evangélikus Fasori Gimnáziumban tanult és érettségizett, mint Neumann, csak majdnem 20 évvel később. Mindkettejüket ma egy emléktábla örökíti meg az iskolában, a hasonlóképpen itt tanult Wigner Jenővel együtt. A szintén János keresztnév viszont már talán igazi véletlen…
4. Didaktikai megjegyzés
Sokféle oktatási struktúrába illeszthetjük a bemutatott játékot. Lehet akkor foglalkozni vele, amikor már valószínűségszámítást tanultak a diákok (legalább a függetlenség esetén a szorzási szabályt és a várható érték fogalmát is bevezettük már). Ekkor ezekre lehet hivatkozni. Ebben az esetben egy modellezési feladatról van szó, amelyhez a szükséges matematika ismert, tehát alkalmazásról beszélhetünk. Van azonban másik lehetőség is, éppen a valószínűségszámítás tanulásának motiválása, amikor pl. az eloszlások és ezek várható értékének bevezetését szeretnék megcélozni. Ekkor a bemutatott feladat már probléma és éppen az a célja a foglalkozásnak, hogy a megoldáshoz milyen „elméletet” kell, hogy fejlesszünk. Ez az út sokkal időigényesebb, de a megértést és a motiváció által a tanulást is segítheti. Bármely lehetőséget is választjuk, célszerű a játékot sokszor eljátszatni, amit időtakarékosságból lehet szabadidős tevékenység terhére és nem a matematika óra idején folytatni. Ott már csak a megfigyelések összegzése történne. A szerző saját tapasztalatai szerint a véletlen stratégia szükségességére rájönnek a tanulók, azonban a következő lépésben segíteni kell, mármint, hogy mit jelent itt a véletlen szerepe és hogyan lehet „alkalmas” véletlent választani. Azaz a várható érték felírása átlagos tanulóknál (ahol a kísérlet folytatódott) segítség nélkül nem várható el. A megoldás ismeretében a kérdés, hogy milyen esetben lenne igazságos, már nem nehéz, ha csak a főátlóban változtathatunk és az 1-est nem így csak a 3-at lehet módosítani. Mivel jelenleg B-nek kedvez a játék, A többet kell, hogy nyerjen, így 3-nál nagyobb szám kell. A számolás ellenőrzésére közöljük a megoldást, amely talán meglepő, de éppen a 4.
5. A játékelmélet további, iskolában is megmutatható alkalmazásai
Ehhez igen gazdag az irodalom, az első ilyen tárgyú munka a már említett Neumann és a közgazdász Morgenstern közös könyve [3]. Egy igazán gazdag tartalmú, didaktikailag is jól felépített és szerteágazó kapcsolatokat bemutató könyv Mérőtől származik [7]. Ebben kezdve a pszichológiától, viselkedés-lélektani, társadalmi és biológiai példák mellett a kvantummechanika ilyen szemléletű bemutatása is szerepel. Az evolúciós biológia területén Dawkins génekről írt könyve [8] tartalmazza annak leírását, hogy miként lehet az evolúció modellezésére ezt az elméletet sok esetben használni. Végül két, még az elmúlt század hetvenes éveiben a Műszaki Kiadónál megjelent könyvet említenénk meg, melyek közül a későbbi [10]-ben még irodalmi alkalmazásokat is olvashatunk, így Sherlock Holmes a híres detektív és a bűnöző Moriarty „párbaját a vonaton”. Méltánytalanul elfeledett, pedig akár középiskolás diákoknak is bátran ajánlható művekről van szó. Közülük a háromszerzős (egyikük Kemény János - már megint János! - magyar származású amerikai matematikus, aki a Basic nyelv kidolgozásával, Neumannhoz hasonlóan a számítástechnikában is jelentőset alkotott. Ő azonban a középiskolát már Amerikában járta ki, mivel az általános iskola elvégzése után zsidó származású szüleivel az Egyesült Államokba menekültek.) Ebben a könyvben [9], elsősorban diszkrét matematikát és valószínűségszámítási témákat dolgoznak fel, mátrixok komoly alkalmazásával. Mégis elemi tárgyalásmódja lehetővé teszi a matematikában kevésbé jártas olvasónak is a megértést, s egyben a modern matematika egyes elemeinek közérthető bemutatását nyújtja, kiváló példát mutatva a népszerűsítésre és a matematika szélesebb közönséghez eljuttatására. Egyben nagyon alkalmas tanárok számára is néhány az iskolában korábban nem szereplő téma egy lehetséges tárgyalására. Azért említem meg, mert a témánkhoz tartozó feladatokat is találhatunk benne.
6. Irodalom
[1] Staar Gy. : A megélt matematika – beszélgetések. Gondolat Kiadó Budapest 1990
[2] Neumann, J.: A kvantummechnika matematikai alapjai. Akadémiai Kiadó, Budapest 1980
[3] Morgenstern, O., von Neumann, J. : Theory of Games and Economic Behavior. University Press Princeton 2004(Először 1944-ben jelent meg, mint a játékelmélet első monográfiája).
[4] Lovász, L.: Algoritmusok bonyolultsága. Egyetemi jegyzet, ELTE Matematikai Intézet A 2014-es változata elérhető: http://www.cs.elte.hu/~kiraly/alg.pdf
[5] Neumann, J. : Zur Theorie der Gesellschaftspiele. Mathematische Annalen, 100. 295– 320. (1928)
[6] Kóczy Á., L. : A Neumann-féle játékelmélet. Közgazdasági Szemle, LIII. évf., 2006. január (31–45. o.) online: http://epa.oszk.hu/00000/00017/00122/pdf/02koczy.pdf
[7] Mérő, L.: Mindenki másképp egyforma. Tercium Kiadó 2007
[8] Dawkins, R.: Az önző gén. Gondolat 1986
[9] Kemeny, Snell, Thompson: A modern matematika alapjai. Műszaki Kiadó 1971
[10] Williams J. D.: Játékelmélet. Műszaki Kiadó 1972
Vancsó Ödön, ELTE TTK
[1] Lénárt István már nagyon sok iskolában elterjedt eszközéről a Lénárt gömbről lehet egy videót megnézni a http://lenartgomb.hu/ honlapon.
[2] Régi játék, amelyet akárhányan játszhatnak. Mindenki 0 vagy 1 vagy 2 egyforma (pl. 5 forintos) pénzérmét tehet a kezébe. A kezdő mond egy számot a kezekbe levő összes pénzérmék számának becslésére, az utána következő hasonlóképpen, de az előző által mondott szám már foglalt. Ezt folytatva mindenki mond sorban egy számot, amely a megelőzőkétől különböző kell, hogy legyen. Az nyer, aki eltalálja a pénzdarabok számának összegét, ha ilyen nincs, akkor az, aki a legközelebbi egész számot mondta. A nyeremény a kezekben levő összes pénzdarab. Döntetlen esetén feleznek (ami akkor lép fel, ha pl. összesen 7 pénzdarab van a kezekben, ezt a számot senki nem mondta, de van 6 és 8 is tippként).
[3] Lásd pl. a Wikipédián: https://hu.wikipedia.org/wiki/Andrej_Nyikolajevics_Kolmogorov
[4] Kevert stratégia azt jelenti, hogy nem az egyiket vagy a másikat választom szisztematikusan, hanem, véletlen szerint „keverem” a választásomat minden egyes partiban. Az egyes stratégiákhoz tartozó valószínűségértékeknek van mindig optimális választása, erről szól a tétel.
[5] Róla még egy kiváló könyv és annak filmfeldolgozása is született „Egy csodálatos elme” címmel.









