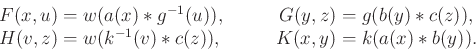Aczél János élete és munkássága

1. Élete

Aczél János 1924. december 26-án született Budapesten és 2020. január 1-jén hunyt el a kanadai Waterlooban. Tanulmányait Budapesten végezte, matematika-fizika tanárszakon. 1947-ben doktorált matematikai analízisből Fejér Lipót és Riesz Frigyes vezetésével. Első eredményeit a középértékek elméletében érte el. A szegedi egyetem Bolyai Intézetében lett tanársegéd, majd egyetemi docensi és tanszékvezetői kinevezést kapott az új Miskolci Egyetemre. 1952-től a debreceni Kossuth Lajos Tudományegyetemen a Matematikai Intézet Analízis Tanszékének első vezetője lett.

Aktív tudományos és tudományszervező munkásságának köszönhetően ebben az időszakban itthon és külföldön egyaránt a függvényegyenletek elméletének vitathatatlan szakértőjévé, gyarapítójává vált, és ezt az elismertségét csak fokozta az 1961-ben megjelent „Vorlesungen über Funktionalgleichungen und ihre Anwendungen” című monográfiája [4], amelyet később 1966-ban bővítetten angolul is publikált az Academic Press [5]. Az első International Symposium on Functional Equations elnevezésű konferenciát 1962-ben Oberwolfachban szervezte meg. Az ebből a rendezvényből létrejött konferenciasorozat a függvényegyenletek művelőinek évenkénti legfontosabb összejövetele. A debreceni évei alatt ma is létező tudományos iskolát hozott létre. 1968-ban megalapította az Aequationes Mathematicae folyóiratot, amely a témakör vezető tudományos újságja.

1965. januárjában családjával elhagyta Magyarországot és rövidesen a kanadai Waterloo Egyetemen lett egyetemi tanár. Haláláig professor emeritusként kötődött ehhez az intézményhez. Kanadai évei alatt nem szakadtak meg magyarországi kapcsolatai, továbbra is támogatta és együtt dolgozott volt debreceni tanítványaival és azok tanítványaival. Így született meg Daróczy Zoltánnal közösen írt [15] könyve: „On measures of information and their characterizations” címmel, amelyet az Academic Press adott ki 1975-ben.

Aczél János a függvényegyenletek elméletének csaknem minden kérdésével, azok minden aspektusával foglalkozott. Eredményeket ért el az általános megoldások leírásában, a regularitási tételek igazolásában, az absztrakt struktúrákon értelmezett egyenletek vizsgálatában. Kutatásaira jellemző, hogy a tiszta matematikai problémák vizsgálata mellett mindig törekedett elért eredményeinek az az információelmélet, a valószínűségszámítás, a közgazdaságtan, a viselkedés tudományokbeli alkalmazására. Eredményeit ma is széles körben idézik, a Google Scholar szerint több mint 13 ezren hivatkoztak munkáira. A MathSciNet és Zentralblatt szerint 9 monográfiát írt ([4], [5], [6], [7], [8], [9], [10], [16], [18]), folyóirat közleményeinek száma pedig meghaladja a 260-at. Társzerzőinek száma 80, 5 vagy annál több dolgozata van Daróczy Zoltánnal, Bruno Fortéval, Hosszú Miklóssal, Palaniappan Kannappannal, Duncan Luce-szal, Maksa Gyulával, Anthony Marley-val, Che Tat Ng-vel és Páles Zsolttal.

Aczél János és Fuchs László

Öt egyetem, köztük 2003-ban a Debreceni Egyetem adományozott neki díszdoktori címet. A kanadai Royal Society 1971-ben választotta tagjai sorába. 1988-ban elnyerte a spanyolországi Santiago Ramón y Cajal Medal-t. Az MTA külső tagja 1990-ben lett. 2008-ban a világ legrégebbi matematikai társaságának, a Hamburgi Mathematical Society tiszteletbeli tagjának is megválasztották.

Hihetetlenül nagy kapcsolatrendszerrel rendelkezett és az így létrejött barátságokat, tudományos együttműködéseket lelkesen és rendszeresen ápolta. A konferenciák szüneteiben, az esti beszélgetések, borozások során a fiatal pályakezdő és a már érett kutatókhoz is mindig érdeklődéssel szólt, bátorított, de finoman kritizált is. Az általa szervezett konferenciákon mindig volt „Problem Session”, ahol a résztvevők nyitott problémáikat tették közzé, és ez számos esetben későbbi kooperációhoz vezetett. Életéről és emlékeiről sokat tudhattunk meg a vele való találkozások során. Emberi tulajdonságai közül talán a humorérzékét, a csodálatos vicc és anekdota mesélő képességét érdemes megemlíteni. Egy kedvenc viccét szeretném felidézni, ezt még a 80-as években, az orosz megszállás utolsó éveiben hallottam tőle először.

Kohn elmegy a rabbihoz és kérdi, hogy lehetséges-e az, hogy a szovjet csapatok valahogy elhagyják Magyarországot. A rabbi így válaszol: Igen, ez kétféleképpen is lehetséges: természetes módon, vagy egy csoda bekövetkezésével. Mi lenne a természetes mód kérdi Kohn. Hát Isten leküldi az arkangyalait és azok kiűzik a szovjeteket válaszol a rabbi. És mi lenne csodával határos lehetőség? Hát, hogy maguktól hagyják el az országot.

Aczél Jánossal – többek között – Daróczy Zoltán készített interjút 2004-ben [27]. Ennek angol fordítása [28] 2015-ben jelent meg. Ebben az interjúban Aczél János gyerekkoráról, tanulmányairól, tanárairól, életének meghatározó fordulatairól beszél. Aki tehát további részleteket szeretne megtudni, annak ezeket a forrásokat ajánljuk.

A továbbiakban Aczél János tudományos eredményeiből válogatunk. Szinte lehetetlen lenne a teljes tevékenységét áttekinteni és összefoglalni. Így a cikk írója a neki legfontosabbnak tűnő eredményeket emelte ki, válogatása teljes mértékben szubjektív.

2. Asszociatív műveletek

A valós számok összeadása és szorzása közötti nyilvánvaló de alapvetően fontos az alábbi kapcsolat:

$\displaystyle x\cdot y=\exp\big(\log(x)+\log(y)\big)\qquad(x,y\in \mathbb{R}_+)$

Más szóval a szorzás „kifejezhető” az összeadás segítségével. Ez az észrevétel motíválja azt, hogy tekintsük az olyan $*$ binér műveleteket, amelyek az

$\displaystyle x*y:=f^{-1}\big(f(x)+f(y)\big) \qquad(x,y\in I)$

(1)

képlettel értelmezettek, ahol $I\subseteq\mathbb{R}$ egy intervallum és $f\colon I\to\mathbb{R}$ egy olyan folytonos és szigorúan monoton függvény, amelynek értékkészlete zárt az összeadásra. Ekkor könnyen látható, hogy a $*$ művelet asszociatív és kommutatív. Az is látható, hogy minden ilyen alakú művelet kancellatív is, ami azt jelenti, hogy minden $x,y,z\in I$ esetén az $x*z=y*z$ , illetve $z*x=z*y$ egyenlőségekből $x=y$ következik. Egy 1948-ban megjelent [3] dolgozatában Aczél János a fenti észrevételnek az alábbi megfordítását igazolta:

1. tétel Legyen $I\subseteq\mathbb{R}$ egy intervallum és $*\colon I\times I\to I$ egy folytonos asszociatív és kancellatív binér művelet $I$ -n. Ekkor létezik egy olyan $f\colon I\to\mathbb{R}$ folytonos és szigorúan monoton függvény, amelynek értékkészlete zárt az összeadásra, hogy (1) teljesül.

Ennek a tételnek egy azonnali és érdekes következménye, hogy ha $*$ egy folytonos asszociatív és kancellatív binér művelet $I$ -n, akkor egyúttal kommutatív is.

Az 1. tétel bizonyításának vázlata. Aczél eredeti cikkében az $f^{-1}$ függvény került megkonstruálásra és a bizonyításban számos esetet kellett megkülönböztetni. A [26] dolgozatban sikerült egy eset-szétválasztás mentes bizonyítást találni, amelyben közvetlenül az $f$ függvényt konstruáljuk meg. Ennek a dolgozatnak az alapötletét ismertetjük.

Az általánosság megszorítása nélkül feltehető, hogy van egy olyan $c\in I$ elem, hogy $c<c*c$ . Ha $x\in I$ , akkor legyen

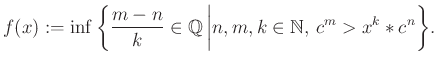
$\displaystyle f(x):=\inf\bigg\{\frac{m-n}{k}\in\mathbb{Q}\,\bigg\vert n,m,k\in\mathbb{N},\, c^m>x^k*c^n\bigg\}.$

Megmutatható, hogy az így definiált $f\colon I\to\mathbb{R}$ függvénnyel az (1) összefüggés valóban teljesül.

Ha az asszociativitás egyenletében a binér művelet minden elfordulását egy potenciálisan különböző binér műveletre cseréljük, akkor az

$\displaystyle F(x,G(y,z))=H(K(x,y),z) \qquad(x\in X,\,y\in Y,\, z\in Z).$

(2)

függvényegyenlethez jutunk, amit az általánosított asszociativitási egyenletnek nevezünk. Ebben $F\colon X\times U\to W$ , $G\colon Y\times Z\to U$ , $H\colon V\times Z\to W$ és $K\colon X\times Z\to V$ az ismeretlen függvények és $X,Y,Z,U,V,W$ nemüres halmazok. Ennek az egyenletnek a megoldásával kapcsolatban Aczél János, V. D. Belousov és Hosszú Miklós 1960-ban publikált [13] dolgozatukban az alábbi eredmény érték el. Ez lényegét tekintve azt állítja, hogy (2) megoldásai egyetlen asszociatív művelet segítségével fejezhetők ki.

2. tétel Legyenek $X,Y,Z,U,V,W$ nemüres halmazok és legyen $(S,*)$ egy félcsoport. Legyenek továbbá $w\colon S\to W$ , $a\colon X\to S$ , $b\colon X\to S$ , $c\colon X\to S$ tetszőleges és $g\colon S\to U$ és $k\colon S\to V$ pedig bijektív leképezések, valamint legyen $x\in X,\,y\in Y,\, z\in Z,\, u\in U,\, v\in V$ esetén

$\begin{displaymath}\begin{array}{r@{\;}lr@{\;}l} F(x,u)&=w(a(x)*g^{-1}(u)), &\qq... ...)&=w(k^{-1}(v)*c(z)), &\qquad K(x,y)&=k(a(x)*b(y)). \end{array}\end{displaymath}$

(3)

Ekkor az $(F,G,H,K)$ fügvénynégyes megoldása a (2) általánosított asszociativitási egyenletnek.

Megfordítva, ha $F\colon X\times U\to W$ , $G\colon Y\times Z\to U$ , $H\colon V\times Z\to W$ , $K\colon X\times Z\to V$ a (2) egyenlet olyan megoldásai, amelyek minden változójukban injektívek (a másik változó tetszőleges rögzitése mellett), akkor létezik egy $(S,*)$ egy félcsoport, létezik $w\colon S\to W$ , $a\colon X\to S$ , $b\colon X\to S$ , $c\colon X\to S$ injektív továbbá $g\colon S\to U$ és $k\colon S\to V$ pedig bijektív leképezés, hogy minden $x\in X,\,y\in Y,\, z\in Z,\, u\in U,\, v\in V$ esetén (3) teljesül.

A tétel elegendőségi részének bizonyítása az $F,G,H,K$ függvények (3)-beli alakjából és a $*$ művelet asszociativitásából könnyen következik. A fordított irányú állítás igazolása sokkal trükkösebb, ehhez az eredeti [13] mű tanulmányozását ajánljuk. Az asszociativitás témakörével kapcsolatban még a [11], [24], [41], [39], [40] dolgozatokat ajánljuk az olvasó figyelmébe.

3. Kiterjesztési tételek

A függvényegyenletek elméletében alapvető az additivitás Cauchy-tól származó függvényegyenlete:

$\displaystyle f(x+y)=f(x)+f(y) \qquad(x,y\in\mathbb{R}),$

(4)

ahol $f\colon \mathbb{R}\to\mathbb{R}$ . Ennek az egyenletnek a megoldásait additív függvényeknek nevezzük. Folytonosság feltételezése mellett könnyű kimutatni, hogy az egyenlet minden megoldása $f(x)=f(1)x$ alakú, azaz lineáris. Másrészt, a valós számok halmazát a racionális számok teste feletti vektortérként felfogva, megmutatható, hogy ennek a vektortérnek bármely Hamel-bázisán értelmezett függvény egyértelműen kiterjeszthető egy additív függvénnyé. Ebből az is következik, hogy az egyenletnek vannak nem lineáris megoldásai, sőt ezek vannak „többségben”.

Amikor függvényegyenletek megoldásáról beszélünk, akkor ez nagyon sokszor azt jelenti, hogy a megoldást egyszerűbb függvényegyenletek megoldásainak és standard, vagy néha tetszőleges függvények segítségével kifejezzük. Ennek a módszernek egy alapvető lépése, hogy néha a megoldás során nyert függvényegyenletek csak egy részhalmazon teljesülnek. Így fontos kérdés, hogy milyen kapcsolat van a leszűkített egyenlet és az eredeti egyenlet között. Példaként tekintsük a (4) egyenlet alábbi leszűkítését:

$\displaystyle f(x+y)=f(x)+f(y) \qquad(x,y>0),$

(5)

ahol $f\colon (0,\infty)\to\mathbb{R}$ . Az nyilvánvaló, hogy (4) minden megoldása eleget tesz (5)-nek. A fenti implikáció megfordíthatóságát Erdős és Aczél [17] ismerték fel az alábbi tételben.

3. tétel Legyen $f\colon (0,\infty)\to\mathbb{R}$ egy olyan függvény, amely kielégíti (5)-öt. Ekkor $f$ egyértelműen kiterjeszthető az $\mathbb{R}$ halmazra, úgy hogy a kiterjesztése pedig teljesíti (4)-et.

Ennek a tételnek a bizonyítása nem különösebben nehéz, de annak felismerése, hogy a kiterjesztési tételek hasznosak és fontosak innen eredeztethető. Ennek a tételnek megszületése óta számos általánosítása és alkalmazása született. A teljesség igénye nélkül az olvasó figyelmét a következő dolgozatokra hívjuk fel: [12], [19], [30], [29], [31], [35], [36], [37], [44], [45], [46].

4. A kváziaritmetikai közepek jellemzése

Egy $I$ intervallumon értelmezett $M$ közép alatt egy olyan $M\colon \bigcup_{n=1}^\infty I^n\to I$ függvényt értünk, mely teljesíti a

$\displaystyle \min(x_1,\dots,x_n)\leq M(x_1,\dots,x_n) \leq \max(x_1,\dots,x_n) \qquad(n\in\mathbb{N},\,(x_1,\dots,x_n)\in I^n)$

egyenlőtlenséget. Egy $M$ közép $n$ -változós leszűkítését, azaz az $M\vert _{I^n}$ függvényt atovábbiakban $M_n$ -nel jelöljük.

A közepek egy fontos osztályát, a kváziaritmetikai közepeket a következőképpen értelmezhetjük: Valamely $f\colon I\to\mathbb{R}$ szigorúan monoton és folytonos függvény esetén legyen

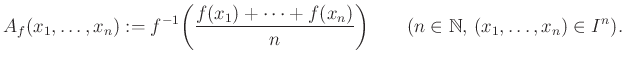
$\displaystyle A_f(x_1,\dots,x_n):=f^{-1}\bigg(\frac{f(x_1)+\dots+f(x_n)}{n}\bigg) \qquad(n\in\mathbb{N},\,(x_1,\dots,x_n)\in I^n).$

Az így értelmezett $A_f\colon \bigcup_{n=1}^\infty I^n\to I$ leképezést az $f$ függvény által generált kváziaritmetikai középnek nevezzük. Az $f(x)=x$ , $f(x)=\ln(x)$ és $f(x)=1/x$ generáló függvényekkel kapott kváziaritmetikai közepekről könnyen látható, hogy ezek a számtani, a mértani, illetve a harmonikus középpel egyenlőek. Ezeknek a közepeknek az elméletét Hardy, Littlewood és Pólya fektette le a múlt század 30-as éveiben [32] monográfiában. Az elmélet egyik legszebb eredménye a következő Kolmogorovtól [34] származó jellemzési tétel.

4. tétel Legyen $M\colon \bigcup_{n=1}^\infty I^n\to I$ . Ekkor $M$ pontosan akkor kváziaritmetikai, azaz $M=A_f$ valamely $f\colon I\to\mathbb{R}$ szigorúan monoton és folytonos függvényre, ha $M$ rendelkezik az alábbi tulajdonságokkal:

(1) $M$ reflexív, azaz $M_n(x,\dots,x)=x$ minden $n\in\mathbb{N}$ és $x\in I$ esetén.

(2) Minden $n\in\mathbb{N}$ -re az $M$ közép $n$ -változós leszűkítése szimmetrikus, folytonos és mindegyik változójában szigorúan monoton növekvő az $I^n$ halmaz felett.

(3) $M$ rendelkezik az alábbi csoportosítási tulajdonsággal: Minden $n,m\in\mathbb{N}$ , $(x_1,\dots,x_n)\in I^n$ és $(y_1,\dots,y_m)\in I^m$ esetén

$\displaystyle M_{n+m}(x_1,\dots,x_n,y_1,\dots,y_m)=M_{n+m}(x_1,\dots,x_n,y,\dots,y),$

ahol $y=M_m(y_1,\dots,y_m)$ .

Annak a bizonyítása, hogy bármely kváziaritmetikai közép rendelkezik a fenti tulajdonságokkal egyszerű. A bizonyítás fő nehézsége a fordított irányú implikáció igazolása, ez a [34] dolgozat fő érdeme.

A fenti jellemzés harmadik (a csoportosításra vonatkozó) tulajdonságának egyik jellegzetessége az, hogy az $M$ közép különböző változószámú leszűkítései között állapít meg egy kapcsolatot. Emiatt a rögzített változószámú közepekről ennek a tételnek segítségével nem lehet eldönteni, hogy káziaritmetikai szerkezetűek-e. Ezt a hiányosságot felismerve Aczél János és a rögzített változószámú közepekre bevezette a biszimmetria fogalmát 1947–48-ban megjelent [1], [2] dolgozataiban.

Egy $M_n\colon I^n\to I$ függvényt biszimmetrikusnak mondunk, ha bármely $I$ -beli elemekből álló $(x_{i,j})$ $n\times n$ -es mátrix esetén

$\displaystyle M_n(M_n(x_{1,1},\dots,x_{1,n}),\dots,M_n(x_{n,1},\dots,x_{n,n}))=M_n(M_n(x_{1,1},\dots,x_{n,1}),\dots,M_n(x_{1,n},\dots,x_{n,n})).$

A [1] dolgozatban ennek a fogalomnak a segítségével az alábbi tételt igazolta.

5. tétel Legyen $n\geq2$ . Ekkor egy $M_n\colon I^n\to I$ függvény pontosan akkor kváziaritmetikai, azaz $M_n$ egy $A_f$ kváziaritmetikai közép $n$ -változós leszűkítése, ha $M_n$ rendelkezik az alábbi tulajdonságokkal:

(1) $M_n$ reflexív.

(2) $M_n$ szimmetrikus, folytonos és mindegyik változójában szigorúan monoton növekvő az $I^n$ halmaz felett.

(3) $M$ biszimmetrikus.

Annak kimutatása, hogy minden $n$ -változós közép eleget tesz a fenti tétel feltételeinek egyszerű. A megfordítás igazolása a következő szép ötleten alapul, amit az egyszerűség kedvéért $n=2$ esetén mutatunk be. Tegyük fel, hogy $M_2$ teljesíti a tétel (1), (2), (3) feltételeit és értelmezzük az $M_{2^n}\colon I^{2^n}\to I$ függvénysorozatot az alábbi rekurzióval:

$\displaystyle M_{2^{n+1}}(x_1,\dots,x_{2^{n+1}}):=M_2\big(M_{2^{n}}(x_1,\dots,x_{2^{n}}),M_{2^{n}}(x_{2^{n}+1},\dots,x_{2^{n+1}})\big).$

Ekkor megmutatható, hogy ez a függvénysorozat eleget tesz a Kolmogorov-tétel összes feltételének, ha az azok megfogalmazásában szereplő $n,m$ számok $2$ hatványai. Pl. $M_{2^{n+1}}$ szimmetriája az $M_2$ szimmetriája és biszimmetriája, valamint $M_{2^{n}}$ szimmetriája segítségével látható be. Ezután Kolmogorov eredeti bizonyítását adaptálva erre a középsorozatra adódik, hogy $M_2,M_4,M_8,\dots$ egy kváziaritmetikai közép 2, 4, 8, ...-változós leszűkítései.

A biszimmetria fogalma és ezek különféle általánosításai kulcsfontosságúnak bizonyultak a függvényegyenletek elméletében és ennek közgazdasági, döntéselméleti alkalmazásaiban. Az egyik érdekes és fontos alkalmazási terület az úgy nevezett konzisztens aggregációval kapcsolatos. További tanulmányozásra ajánlva (a teljesség igénye nélkül) megemlítjük a [20], [21], [22], [23], [33], [38], [42], [43], [44] dolgozatokat.

5. A Bajraktarević-közepek homogenitása

Az ötvenes évek végén egy bosnyák matematikus, M. Bajraktarević a kváziaritmetikai közepek következő általánosítását vezette be [25] dolgozatában. Legyenek $f,g\colon I\to\mathbb{R}$ olyan folytonos függvények, hogy $g$ pozitív és $f/g$ szigorúan monoton $I$ -n. Értelmezzük a $B_{f,g}\colon \bigcup_{n=1}^\infty I^n\to I$ közepet az alábbi képlettel:

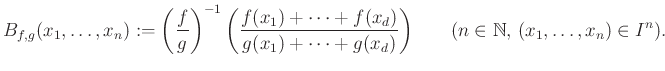$\displaystyle B_{f,g}(x_1,\dots,x_n):=\left(\frac{f}{g}\right)^{-1}\bigg(\frac{... ...d)}{g(x_1)+\dots+g(x_d)}\bigg) \qquad(n\in\mathbb{N},\,(x_1,\dots,x_n)\in I^n).$

(6)

Ha $g\equiv1$ , akkor látható, hogy $B_{f,g}$ az $A_f$ kváziaritmetikai középre egyszerűsödik. Ezekről a közepekről kiderült, hogy a Shannon-entrópia általánosítást jelentő Rényi-entrópiákat ilyen típusú közepek logaritmusaként lehet előállítani. Így fontos kérdéssé vált az olyan Bajraktarević-közepek megtalálása, amelyek homogének, azaz, amelyek teljesítik az alábbi függvényegyenletet:

$\displaystyle B_{f,g}(tx_1,\dots,tx_n)=tB_{f,g}(x_1,\dots,x_n) \qquad(n\in\mathbb{N},\,t>0,\,(x_1,\dots,x_n)\in \big(I\cap\tfrac{1}{t}I\big)^n).$

A probléma előtörténeteként Hardy, Littlewood és Pólya [32] könyvéből ekkor már jól ismert volt, hogy a kváziaritmetikai közepek között pontosan a hatványközepek a homogének. Végül a választ a fenti kérdésre Aczél és Daróczy találták meg 1963-ban megjelent [14] cikkében.

6. tétel Legyen $I$ a pozitív valós számok egy reciprokképzésre nézve invariáns részintervalluma és legyenek $f,g\colon I\to\mathbb{R}$ olyan folytonos függvények, hogy $g$ pozitív és $f/g$ szigorúan monoton $I$ -n. Ekkor a $B_{f,g}$ közép pontosan akkor homogén, ha léteznek olyan $p,q\in\mathbb{C}$ komplex számok, hogy vagy $p,q\in\mathbb{R}$ , vagy $p=\overline{q}$ és $B_{f,g}$ egyenlő a $G_{p,q}\colon \bigcup_{n=1}^\infty I^n\to I$ általánosított Gini-középpel, amely következőképpen van értelmezve:

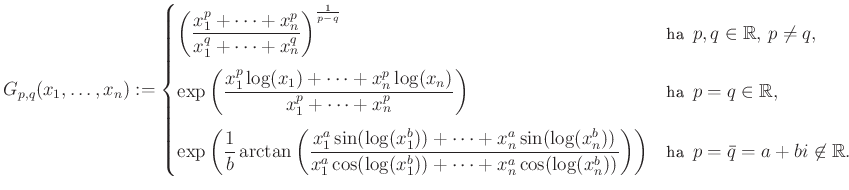
$\displaystyle G_{p,q}(x_1,\dots,x_n):=\begin{cases} \bigg(\dfrac{x_1^p+\dots+x_... ...(x_n^b))}\right)\right) &\text{ha }p=\bar{q}=a+bi\not\in\mathbb{R}. \end{cases}$

Ennek a tételnek fontos alkalmazásai találhatók Aczélnak és Daróczynak az információmértékekről írott [15] monográfiájában, amely a két szerző egyik leghivatkozottabb közös műve. A Google Scholar szerint ez a könyv eddig több mint 1200 hivatkozást kapott.

6. Zárszó

Reméljük, hogy a fenti válogatással felkeltettük a tisztelt olvasó érdeklődését, és tovább folytatja Aczél János eredményeinek megismerését. Ezekből egy kreatív, nagyhatású matematikus képe fog kibontakozni. Emlékét őrzik mindazok, akik ismerték és akik eredményei alapján tisztelik. A nagy öt – a „big five” – negyedik tagja távozott. Sokunknak fog hiányozni.

Irodalomjegyzék

[1] J. Aczél. The notion of mean values. Norske Vid. Selsk. Forh., Trondhjem, 19(23):83–86, 1947.
: [2] J. Aczél. On mean values and operations defined for two variables. Norske Vid. Selsk. Forh., Trondhjem, 20(10):37–40, 1948.
: [3] J. Aczél. Sur les opérations définies pour nombres réels. Bull. Soc. Math. France, 76:59–64, 1948.
: [4] J. Aczél. Vorlesungen über Funktionalgleichungen und ihre Anwendungen. Birkhäuser, Basel, 1961. Lehrbücher und Monographien aus dem Gebiete der exakten Wissenschaften, Mathematische Reihe, Bd. 25.
: [5] J. Aczél. Lectures on Functional Equations and Their Applications, volume 19 of Mathematics in Science and Engineering. Academic Press, New York–London, 1966.
: [6] J. Aczél. On Applications and Theory of Functional Equations. Birkhäuser, Basel, 1969. Elemente der Mathematik vom höheren Standpunkt, Band V.
: [7] J. Aczél. Functional Equations and Inequalities. Edizioni Cremonese, Rome, 1971. Centro Internazionale Matematico Estivo (C.I.M.E.), III Ciclo, La Mendola, August 20–28, 1970, Coordinated by B. Forte.
: [8] J. Aczél, editor. Functional Equations: History, Applications and Theory. Reidel, Dordrecht, 1984.
: [9] J. Aczél. A Short Course on Functional Equations (Based Upon Recent Applications to the Social and Behavioral Sciences). Reidel, Dordrecht, 1987.
: [10] J. Aczél, editor. Aggregating clones, colors, equations, iterates, numbers, and tiles. Birkhäuser, Basel, 1995. Reprint of Aequationes Math. 50 (1995), no. 1–2.
: [11] J. Aczél. The associativity equation re-revisited. In G. Erikson and Y. Zhai, editors, Bayesian Inference and Maximum Entropy Methods in Science and Engineering, page 195–203. American Institute of Physics, Melville–New York, 2004.
: [12] J. Aczél, J. A. Baker, D. Ž. Djoković, Pl. Kannappan, and F. Radó. Extensions of certain homomorphisms of subsemigroups to homomorphisms of groups. Aequationes Math., 6:263–271, 1971.
: [13] J. Aczél, V. D. Belousov, and M. Hosszú. Generalized associativity and bisymmetry on quasigroups. Acta Math. Acad. Sci. Hungar., 11:127–136, 1960.
: [14] J. Aczél and Z. Daróczy. Über verallgemeinerte quasilineare Mittelwerte, die mit Gewichtsfunktionen gebildet sind. Publ. Math. Debrecen, 10:171–190, 1963.
: [15] J. Aczél and Z. Daróczy. On Measures of Information and Their Characterizations. Academic Press [Harcourt Brace Jovanovich Publishers], New York, 1975. Mathematics in Science and Engineering, Vol. 115.
: [16] J. Aczél and J. Dhombres. Functional Equations in Several Variables. Cambridge University Press, Cambridge, 1989. With applications to mathematics, information theory and to the natural and social sciences.
: [17] J. Aczél and P. Erdős. The nonexistence of a Hamel-basis and the general solution of Cauchy's functional equation for nonnegative numbers. Publ. Math. Debrecen, 12:253–263, 1965.
: [18] J. Aczél and S. Gołąb. Funktionalgleichungen der Theorie der geometrischen Objekte. Państwowe Wydawnictwo Naukowe, Warsaw, 1960. Polska Akademia Nauk. Monografie Matematyczne, Tom 39.
: [19] J. Aczél and L. Losonczi. Extension of functional equations. In The mathematics of Paul Erdős, II, page 251–263. Springer, Berlin, 1997.
: [20] J. Aczél and Gy. Maksa. Solution of the rectangular 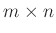$m\times n$ generalized bisymmetry equation and of the problem of consistent aggregation. J. Math. Anal. Appl., 203(1):104–126, 1996.
: [21] J. Aczél and Gy. Maksa. Consistent aggregation and generalized bisymmetry. Trans. Royal Soc. Canada, 6(6):21–25, 1997.
: [22] J. Aczél, Gy. Maksa, and M. Taylor. Equations of generalized bisymmetry and of consistent aggregation: weakly surjective solutions which may be discontinuous at places. J. Math. Anal. Appl., 214(1):22–35, 1997.
: [23] J. Aczél and T. L. Saaty. Procedures for synthesizing ratio judgements. J. Math. Psych., 27(1):93–102, 1983.
: [24] B. Bacchelli. Representation of continuous associative functions. Stochastica, 10(1):13–28, 1986.
: [25] M. Bajraktarević. Sur une équation fonctionnelle aux valeurs moyennes. Glasnik Mat.-Fiz. Astronom. Društvo Mat. Fiz. Hrvatske Ser. II, 13:243–248, 1958.
: [26] R. Craigen and Zs. Páles. The associativity equation revisited. Aequationes Math., 37(2–3):306–312, 1989.
: [27] Z. Daróczy. Beszélgetés Aczél Jánossal. Debreceni Szemle, XII(3):465–481, 2004.
: [28] Z. Daróczy. An interview with János Aczél. Aequationes Math., 89(1):1–16, 2015. Reprint of Debreceni Szemle 3 (2004), no. 12, 465–480.
: [29] Z. Daróczy and L. Losonczi. Über die Erweiterung der auf einer Punktmenge additiven Funktionen. Publ. Math. Debrecen, 14:239–245, 1967.
: [30] Z. Daróczy and Gy. Maksa. Functional equations on convex sets. Acta Math. Hungar., 68(3):187–195, 1995.
: [31] R. Ger. On extensions of polynomial functions. Results Math., 26(3–4):281–289, 1994.
: [32] G. H. Hardy, J. E. Littlewood, and G. Pólya. Inequalities. Cambridge University Press, Cambridge, 1934. (first edition), 1952 (second edition).
: [33] I. Kocsis. A bisymmetry equation on restricted domain. Aequationes Math., 73(3):280–284, 2007.
: [34] A. N. Kolmogorov. Sur la notion de la moyenne. Rend. Accad. dei Lincei (6), 12:388–391, 1930.
: [35] K. Lajkó. Applications of extensions of additive functions. Aequationes Math., 11:68–76, 1974.
: [36] L. Losonczi. An extension theorem. Aequationes Math., 28(3):293–299, 1985.
: [37] L. Losonczi. An extension theorem for the Levi-Civita functional equation and its applications. In D. Gronau, editor, Contributions to the Theory of Functional Equations (Graz, 1991), volume 315 of Grazer Math. Berichte, page 51–68. Karl-Franzens-Univ. Graz, Graz, 1991.
: [38] Gy. Maksa. Solution of generalized bisymmetry type equations without surjectivity assumptions. Aequationes Math., 57(1):50–74, 1999.
: [39] Gy. Maksa. The generalized associativity equation revisited. Rocznik Nauk.-Dydakt. Prace Mat., 17:175–180, 2000.
: [40] Gy. Maksa. CM solutions of some functional equations of associative type. Ann. Univ. Sci. Budapest. Sect. Comput., 24:125–132, 2004.
: [41] Gy. Maksa. Quasisums and generalized associativity. Aequationes Math., 69(1–2):6–27, 2005.
: [42] Á. Münnich, Gy. Maksa, and R. J. Mokken. Collective judgement: combining individual value judgements. Math. Social Sci., 37(3):211–233, 1999.
: [43] Á. Münnich, Gy. Maksa, and R. J. Mokken. 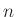$n$ -variable bisection. J. Math. Psych., 44(4):569–581, 2000.
: [44] Zs. Páles. Extension theorem for functional equations with bisymmetric operations. Aequationes Math., 63(3):266–291, 2002.
: [45] J. Rimán. On an extension of Pexider's equation. Zbornik Rad. Mat. Inst. Beograd (N.S.), 1(9):65–72, 1976. Symposium en Quasigroupes et Équations Fonctionnelles (Belgrade-Novi Sad, 1974).
: [46] L. Székelyhidi. An extension theorem for a functional equation. Publ. Math. Debrecen, 28(3–4):275–279, 1981.

Páles Zsolt

Debreceni Egyetem, Matematikai Intézet,
Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.